基于聚氨酯弹性体位移传感器的有限元分析及实验
祖洪飞, 李召兵, 彭来湖
(浙江理工大学 浙江省现代纺织装备技术重点实验室, 浙江 杭州 310018)
近年来,越来越多的创新技术应用到位移传感器中,比如:光栅技术、磁栅技术、磁致伸缩技术、MTS协调加载控制技术和光纤技术等[1]。这些不同原理的位移传感器被广泛应用于航空航天、半导体加工、机械手和生物医学等领域[2]。
目前,国内外学者对位移传感器的研究取得了不少成果。Nie等[3]通过将石墨烯网片粘贴在液晶聚合物基片上,并将其应用于机械振动学中。通过监测应变传感器中石墨烯网片的相对电阻变化,可以检测到结构微小位移引起的应变。Wang等[4]根据电感线圈的磁耦合特性,设计了一种无线无源电路,推导了电阻应变传感器的电阻值与电路总输入阻抗相位的关系,从而实现非接触式的位移测量。Guo等[5]采用直接油墨书写的多层复合结构高精度电阻应变传感器,可优化层平整度和界面强度。周宇等[6]根据激光三角法原理设计了一种激光位移传感器用的收光镜头,实现了工作距离为100 mm,量程为±25 mm的位移测量。张小蝶[7]采用的是磁致伸缩效应和磁致伸缩逆效应均显著的铁磁材料作为敏感元件的位移传感器研究。慕雨松[8]基于相位差滤波原理完成了对增量信号链路的设计和验证实现了ASIC光电芯片在高精度角位移传感器中的创新。上述位移传感器只能测量单一角位移或平面位移,那么可同时动态测量多自由度的位移传感器具有研究价值,尚江坤等[9]通过多个压电陶瓷致动器和激光位移传感器组合设计了一种3自由度定位系统,实现了沿X轴和Y轴移动以及绕Z轴转动的位移测量。
多自由度位移传感器的测量原理主要有2类:一类是通过多个位移传感器组合实现多自由度位移测量,比如张佳炜[10]分别对多个霍尔传感器及信号采集卡实现6自由度测量并进行实验验证,得出单自由度霍尔传感器在4 mm的量程内分辨力达到1 μm,非线性度为1.23%;方国明等[11]采用3个高精度的位移传感器获取待测目标平面3个不共线点的位移量,3个不共线点可以确定平面的法线,利用法线实现了平面的方位角、俯仰角以及轴向位移的测量。另一类是单个位移传感器实现多自由度位移测量,比如余建平等[12]提出了实现大量3自由度位移测量的电容式位移传感器设计方案,在线性位移4 mm内,保证了0.5%的线性度。Saito等[13]采用光学方法实现了3自由度的角位移测量,使用衍射光栅代替平面镜作为目标反射镜,通过衍射光栅反射的3组不同衍射光波信号来完成3自由度角位移测量。在这些不同原理的多自由度位移传感器中,测量范围多是小量程的位移/扭转量,因此能实现大量程、高精度、低成本和多自由度测量的传感器具有研究价值。
课题组基于弹性体位移传感器原理,推导出传感器运动端X,Y和Z方向位移和绕Z轴扭转载荷与固定端X,Y和Z方向的正应变和切应变之间的关系矩阵。在测试聚氨酯弹性体材料拉伸应力应变曲线的基础上,对比分析Mooney-Rivlin、Ogden、Yeoh和Neo-Hooke 4种常用弹性体本构模型,选择最适合聚氨酯弹性体变形行为的材料本构模型及参数。将最合适的本构模型及参数导入ABAQUS软件中,建立位移传感器非线性有限元模型,仿真分析了传感器位移和扭转实验,确定最大应变区域,为传感器中应变片粘贴位置及方式提供依据。
1 弹性体位移传感器
1.1 弹性体位移传感器原理
本研究提出的新型弹性体位移传感器具有精度高、量程大、多自由度测量、机构简单和成本低等特点。基于电阻应变式原理,传感器核心部件是一个能感知多维应力应变并具有低滞回、低蠕变、低阻尼和抗断裂特性的弹性元件。原理如图1所示:弹性感知元件的A端固定,B端有位移、扭转和弯矩载荷。当B端受到载荷时,通过应变片或应变花测量出A端应变变化,确定应变感知元件与被驱动末端的空间位置和扭转角之间的数学模型。当弹性体传感器在空间运动时,通过测得的多个应变量在预先建立的数学模型中转换成弹性体传感器运动端空间位置和扭转角度。Mx,My分别为X,Y方向的弯矩;T为转矩;Fz为Z方向的受力;X/β,Y/α和φ为X,Y和Z方向的扭转角。

图1 位移传感器测量原理Figure 1 Measuring principle of displacement sensor
1.2 弹性体位移传感器实验原理及数学模型
在弹性体位移传感器设计中,弹性体不易像悬臂梁模型一样施加载荷和约束,需要添加夹持部分,就需对弹性体传感器做出改良,如图2所示。在图中,两侧用法兰盘夹持圆柱弹性体位移传感器,左端固定,右端可向X,Y和Z轴方向平移和绕Z轴扭转,可用此弹性体传感器替代X,Y和Z方向上的3个位移传感器和绕Z轴的角位移传感器,实现4个自由度的测量。
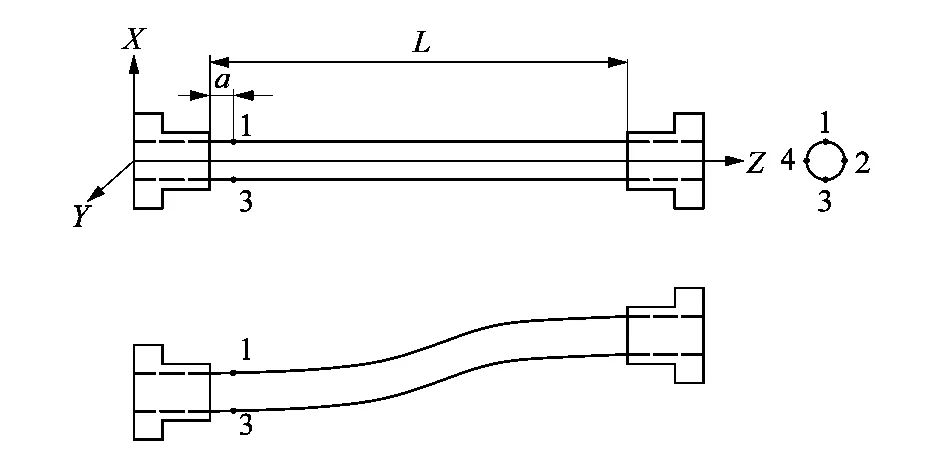
图2 弹性体位移传感器实验测量原理Figure 2 Experimental measurement principle of elastomer displacement sensor
定义D为弹性体的截面直径;L为2法兰盘之间弹性体的长度;a为距离固定端法兰盘的距离;x,y和z为弹性体在X,Y和Z方向上的平移量;φ为扭转角。推导出与固定端法兰盘距离为a的圆柱面上应变εx,εy,εz和γ与右端X,Y,Z方向平移、绕Z轴扭转角之间的关系矩阵:
(1)
1.3 弹性体位移传感器实验
搭建弹性体位移传感器实验平台,如图3所示。在平台上进行位移传感器实验,将位移传感器一端固定在平台底座,另一端固定在机械手运动端,应变片贴片位置参考有限元分析结果中最大应变区域。通过驱动机械手,沿Y轴方向平移30 mm和扭转15° 2种情况进行3次实验,通过应变仪和测试分析系统得出2种情况下应变值并取平均值,得到固定端正应变与运动端位移的关系、切应变与扭转角的关系。弹性体位移传感器实验流程如图4所示。

图3 弹性体位移传感器实验平台Figure 3 Experimental platform of elastomer displacement sensor

图4 弹性体位移传感器实验流程Figure 4 Experimental process of elastomer displacement sensor
2 位移传感器中橡胶类超弹性材料模型
传感器所用的弹性体材料从以下4个方面选取:蠕变小、滞回小、阻尼小及抗断裂性能好。对硅橡胶、天然橡胶和聚氨酯弹性体的这4种性能参数进行对比,选取最适合本实验的是聚氨酯弹性体材料,其材料参数如表1所示。

表1 弹性体材料参数Table 1 Material parameters of elastomer
聚氨酯等橡胶类的超弹性性能反映出其在发生重大变形后能够快速恢复原始状态的能力。因此,超弹性体的本构模型能够描述大应力下的非线性,并且在有限变形条件下具有充分的弹性。目前以应变能密度函数为基础发展出本构理论适用于超弹性材料的大弹性变形,该类变形可用于有限元仿真中。
超弹性材料可表达为“应变势能”U的形式,即在材料点上作为应变函数的每单位参考体积中储藏的应变能。在ABAQUS中,有很多种应变势能形式来近似模拟不同的弹性体,比如:Mooney-Rivlin形式、Ogden形式、Neo-Hooke形式和Yeoh形式等。本实验中的聚氨酯弹性体材料经过单轴拉伸实验拟合出的应力-应变关系,得到最适合聚氨酯材料的本构模型是Ogden式[14]。
Ogden形式的应变势能关系是:
(2)
式中:U是每单位参考体积的应变势能;λi是拉伸偏量;N是材料参数;J是热膨胀中定义的弹性体积比;Di,μi和αi是温度相关的材料参数。
Ogden形式中初始剪切模量和体积模量的公式如下:
(3)
Ogden形式在单轴拉伸、等双轴拉伸和剪切实验中都得到了验证。其中,不管是小变形还是大变形情况下,Ogden形式是能够准确描述材料应力应变关系的一种本构模型。课题组通过下一章节中的单轴拉伸实验数据与各个本构模型拟合曲线对比,选择最为接近的Ogden形式描述聚氨酯橡胶的本构模型。
3 传感器材料单轴拉伸实验与参数的确定
3.1 单轴拉伸实验
实验材料选用传感器所用的聚氨酯弹性体,基于GB/T 528—2009标准,聚氨酯橡胶试样使用厚度为2 mm 、宽为6 mm、标距为25 mm的Ⅰ型哑铃状试样[15],如图5所示。

图5 Ⅰ型哑铃状橡胶标准试件Figure 5 Type 1 dumbbell rubber standard specimen
在万能拉伸压缩试验机上进行单轴拉伸实验,在保持原始状态下夹持聚氨酯橡胶试件以500 mm/min的速度进行拉伸,拉伸的初始位置和拉伸位置如图6~7所示。连续监测拉伸力和变形量的变化值,直到变形量达到250%为止。使用相同材料和尺寸的3组橡胶试样进行实验,并记录数据。

图6 单轴拉伸实验初始位置Figure 6 Initial position of uniaxial tensile test

图7 单轴拉伸实验拉伸位置Figure 7 Tensile position of uniaxial tensile test
3.2 实验数据处理
根据GB/T 528—2009中的方法,对单轴拉伸实验数据进行处理[16]。该方法的理论基础是基于超材料的小变形理论。当材料受到轴向拉伸时,假设试样的横截面积不变或改变很小可忽略不计,其应力和应变为:
(4)
(5)
式中:P为施加在哑铃状试样上的轴向拉伸力,S0为试样拉伸部分的原始横截面积,ΔL为试样的轴向拉伸的变形量,L0为试样拉伸部分的原始长度。
使用以上2个公式,对3组单轴拉伸实验得到的拉伸力与变形之间的关系进行处理,取平均值后,得到聚氨酯橡胶的应力-应变关系。
3.3 本构模型选取
在有限元分析的仿真中,橡胶类超弹性材料的本构模型选择直接关系到整个仿真的结果是否精确。本实验中选取适合单轴拉伸实验的Mooney-Rivlin、Ogden、Yeoh和Neo-Hooke 4种本构模型,将实验数据作为平均值,通过方差分析选取了与聚氨酯弹性体拟合度最好的本构模型。不同本构模型在单轴拉伸实验下拟合曲线如图8所示。因为实验数据都是离散的点,每个点横纵坐标并不相同,所以,通过Origin软件中差值外推法,得到在相同横坐标下,每条曲线的纵坐标值,再将得到的数据拟合曲线,如图9所示;不同本构模型方差如表2所示。

图8 应力应变关系拟合曲线Figure 8 Fitting curve of stress-strain relationship
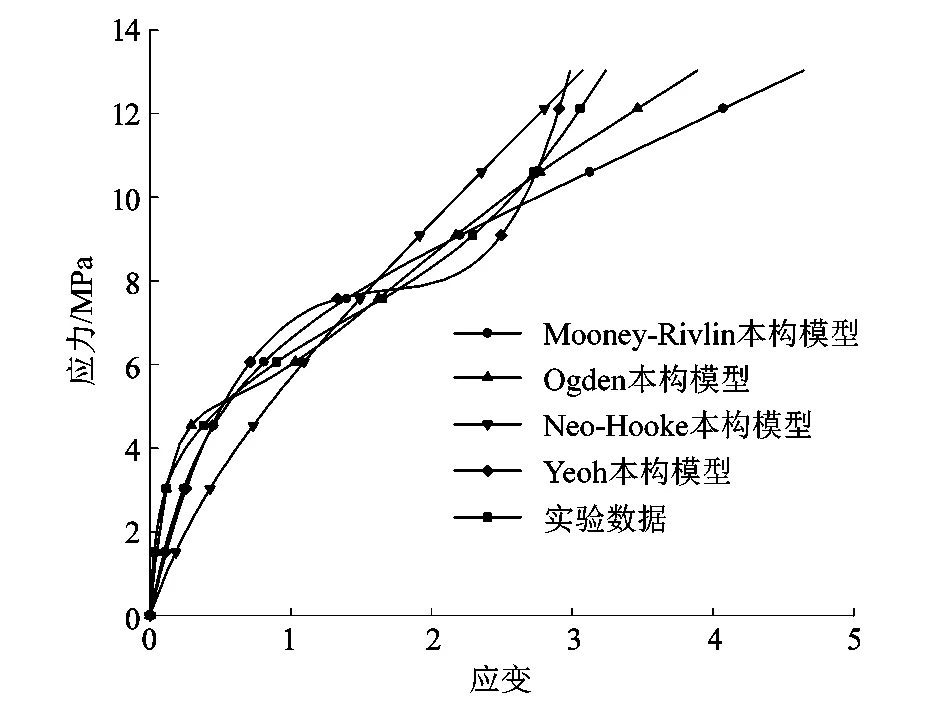
图9 差值外推法拟合曲线Figure 9 Curve fitting by difference extrapolation

表2 不同本构模型拟合曲线的方差Table 2 Variance of fitting curves for different constitutive models
通过对比发现Yeoh本构模型的方差最小,Ogden本构模型方差次之,但从本构模型拟合曲线趋势上看Yeoh本构模型拟合曲线中多次出现拐点,并不适合聚氨酯弹性体,同时,聚氨酯弹性体在传感器中应变范围在0%~100%范围内,Ogden本构模型拟合程度最好。综上所述,最适合聚氨酯弹性体材料的本构模型是Ogden本构模型,其参数如表3所示。

表3 实验数据在Ogden模型下拟合参数Table 3 Fitting parameters of experimental data under Ogden model
4 有限元分析计算结果
4.1 聚氨酯橡胶试件的有限元分析
将图8中应力应变实验数据导入超弹性材料模块,选取Ogden本构模型为聚氨酯材料模型。将SolidWorks中建立聚氨酯橡胶试样三维模型导入ABAQUS中进行分区域网格划分,为使分析结果更正确,其中真实拉伸区域网格划分更细,在Hybrid formulation中选择C3D8RH实体单元类型,采用单元形状为六面体、中性轴画法对网格进行划分,如图10所示。橡胶试件的单元数目为41 832,节点数目为38 957[17]。

图10 聚氨酯橡胶试件网格划分Figure 10 Mesh generation of polyurethane rubber specimen
在分析步中一端添加夹持部分的固定约束,另一端添加位移载荷,模拟实验拉伸聚氨酯橡胶试件80 mm,得出有限元仿真应力云图,如图11所示。为了确保所用本构模型对聚氨酯材料的准确性,又将不同本构模型导入橡胶试件的有限元仿真中,得出仿真与实验的误差,如表4所示。

图11 单轴拉伸实验有限元仿真Figure 11 Finite element simulation of uniaxial tensile test

表4 单轴拉伸实验在不同本构模型下的误差Table 4 Error of uniaxial tensile test under different constitutive models
从图11中可以看到在仿真结果中最大应力处位置在试件的拉伸部分中部边缘。将实验及数据处理后,仿真数据比实验数据大8.70%。将实验结果与其他本构模型进行对比,发现Ogden本构模型是误差最小的,说明聚氨酯弹性体材料可以用Ogden本构模型来描述其特性。
4.2 位移传感器实验模型的有限元仿真
基于弹性体位移传感器,在ABAQUS实体单元中,建立位移传感器的橡胶棒与法兰盘模型,装配体如图12所示,网格划分如图13所示。其中聚氨酯弹性体节点数144 120个,单元数123 600个;单个法兰盘节点数2 040个,单元数1 394个[18]。

图12 装配体模型Figure 12 Assembly model

图13 装配体网格划分Figure 13 Assembly mesh generation
在ABAQUS中Property模块创建聚氨酯弹性体和法兰盘材料模型,将上一章单轴拉伸实验所得应力应变数据以Ogden本构模型导入,得到聚氨酯弹性体材料模型。法兰盘使用6061铝合金,将密度2 810 kg/m3,弹性模量69 000 MPa和泊松比0.3导入法兰盘模型,此仿真的边界条件中法兰盘和弹性体胶合部分最为重要,将3个实体中胶结的相互结合面采用surface-to-surface contact 的方式,导入实验所用的胶水参数,连接方式选用胶结方式建立胶结的边界条件。在Load模块添加约束和载荷,根据实验,将位移传感器一端对法兰盘添加固定约束,另一端对法兰盘施加位移30 mm和扭转角15°的载荷,最后得到的有限元分析应变云图如图14~15所示。

图14 平移仿真云图Figure 14 Cloud image of translation simulation

图15 扭转仿真云图Figure 15 Cloud image of torsion simulation
在沿Y轴正方向位移30 mm的平移仿真云图中可以看出,应变分布是对称的,最大应变值出现在与平移相反方向一侧且距离固定端法兰盘4 mm处,所以测量正应变的应变片应贴在距离固定端法兰盘4 mm处。贴片方向应平行于弹性体轴线,沿周向平均分布4个应变片以测量X,Y方向上的应变变化情况,如图16所示。
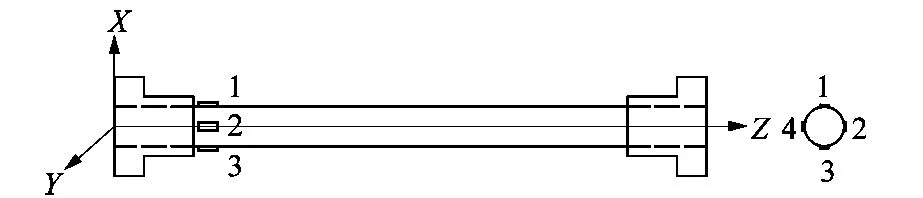
图16 测量正应变的应变片贴片位置Figure 16 Position of strain gauge for measuring positive strain
在绕Z轴扭转15°的仿真云图中可以看出,在整个弹性体上的切应变都是一样的且为最大值,所以,测量切应变的应变片贴片方向选择垂直于弹性体轴线。为了不影响两侧应变片的添加,贴片位置选择在弹性体中部表面,如图17所示。

图17 测量切应变的应变片贴片位置Figure 17 Position of strain gauge for measuring shear strain
4.3 位移传感器有限元仿真结果与实验对比
在平移仿真中,导出1号应变片位移量与正应变的关系;在扭转仿真中,导出5号应变片扭转角度与切应变的关系。在实验中,分别驱动机械手位移30 mm和扭转15°,重复3次取平均值得出1号应变片正应变与位移的关系,5号应变片切应变与扭转角度的关系,如图18~19所示。
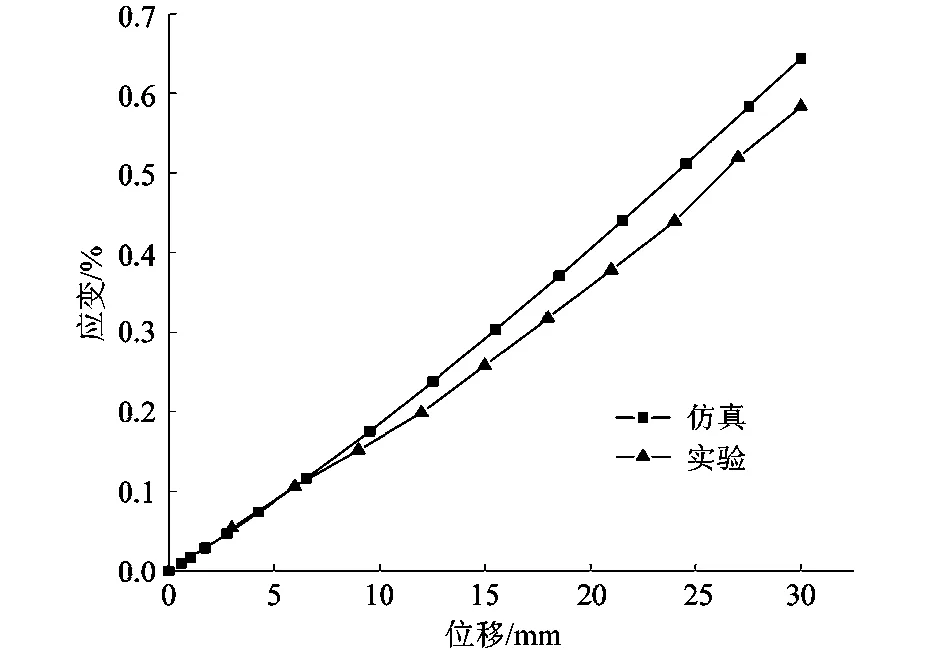
图18 1号应变片正应变与位移关系Figure 18 Relationship between normal strain and displacement of strain gauge No.1

图19 5号应变片切应变与扭转角度关系Figure 19 Relationship between shear strain and torsion angle of strain gauge No.5
当传感器运动端是位移载荷时,仿真和实验结果的最大误差为9.31%;当传感器运动端是扭转载荷时,仿真和实验结果最大误差是8.75%。传感器的实验与仿真误差在10%以内,符合此传感器要求。
5 结论
课题组通过聚氨酯弹性体国标试验片单轴拉伸实验获得聚氨酯橡胶的应力-应变关系,确定适合聚氨酯弹性体的本构模型及参数;并对聚氨酯弹性体传感器实验模型进行有限元分析,将传感器根部应变与端部位移、扭转之间关系的仿真结果与传感器实验结果对比分析。根据分析,可以得出如下结论:
1) 通过在弹性元件上粘贴应变片,测量分析弹性元件的应变与施加位移/扭转载荷之间的关系,实现传感器4个自由度位移/扭转的测量,推导出应变与载荷之间的关系矩阵。
2) 通过实验拟合出聚氨酯弹性体材料应力应变曲线得出拟合度最高的本构模型为Ogden本构模型,并得出相关参数值N=3,μ1=-4.186 339 96,μ2=-5.274 235 69,μ3=23.547 311 40,α1= 3.034 209 10,α2=3.043 093 58,α3=-5.851 101 80,D=0。
3) 通过有限元仿真,确定传感器中应变片贴片位置及方向。测量正应变的应变片粘贴在距离固定端法兰盘4 mm处。贴片方向平行于弹性体轴线,且沿周向平均分布4个应变片;测量切应变的应变片贴片方向选择垂直于弹性体轴线,贴片位置选择在弹性体中部表面。
4) 通过位移和扭转2种工况的有限元分析的与实验数据对比,当传感器运动端是位移载荷时,仿真和实验结果的最大误差为9.31%;当传感器运动端是扭转载荷时,仿真和实验结果最大误差是8.75%。传感器的实验与仿真误差在10%以内,符合此传感器要求。

