剑杆织机碳纤剑带包绕传剑轮的约束载荷特征

朱金杰， 周香琴

(浙江理工大学 浙江省现代纺织装备技术重点实验室， 浙江 杭州 310018)

碳纤剑带是剑杆织机引纬机构中的关键零件，由纵横2个方向交替的多层碳纤与环氧树脂结合而成，具有一定的刚度和挠性。剑带压块把碳纤剑带约束在传剑轮上，由传剑轮带动剑头运动，从而实现引纬。由于碳纤剑带相对其他挠性剑带具有更大的刚度，因此梭口内无需导钩约束，对织物品种适应性很好，深受使用者欢迎；但碳纤剑带包绕在传剑轮上需要较大的约束力，运行过程中剑带温度较高，容易出现剑带开裂磨损等问题。为了提高设备性能，研究碳纤剑带包绕在传剑轮上的约束载荷特征，可为剑杆织机的使用提供更科学的依据，具有较高工程意义。目前有学者研究了引纬机构中传剑轮载荷特性[1]，引纬机构中剑杆及剑带的运动规律[2-3]，引纬机构中剑带润滑导向机构设计[4]，引纬机构的载荷特征[5-7]，剑带在剑箱中的变形[8]，剑带孔加工冲压模具及加工工艺[9]，以及剑带冷却装置[10]，但对于引纬过程中剑带磨损、断裂、损坏原因的探索以及改进措施的研究相对较少。因此课题组通过分析碳纤剑带在传剑轮处的约束特征，研究碳纤剑带所受的约束载荷及其影响因素，针对影响因素提出完善措施，从而提高剑带使用寿命，为剑杆织机的设计和稳定运行提供合理的建议。

1 碳纤剑带的约束特征

碳纤剑带的工作环境如图1所示。引纬机构中碳纤剑带1在传剑轮2的带动下，从剑库3中牵引而出(剑带在剑库中被约束只能沿剑库方向运动)，在剑带压块4、剑带压块6约束下包绕在传剑轮上，在传剑轮的外部，碳纤剑带由剑库3和静导轨7约束。工作时，传剑轮顺时针转动，带动碳纤剑带和剑头从剑库出来，经过传剑轮和静导轨，进入梭口，把纬纱交给右侧剑头；随后，传剑轮逆时针转动，带动碳纤剑带经过静导轨和传剑轮回到剑库，完成了一次引纬工作。在该运动过程中，碳纤剑带在剑库内的长度始终在变化，但总有一部分碳纤剑带留在剑库和静导轨中。剑带在剑带压块4和6处受到约束力，在约束力的作用下，碳纤剑带实现直线运动与圆弧运动的转变。

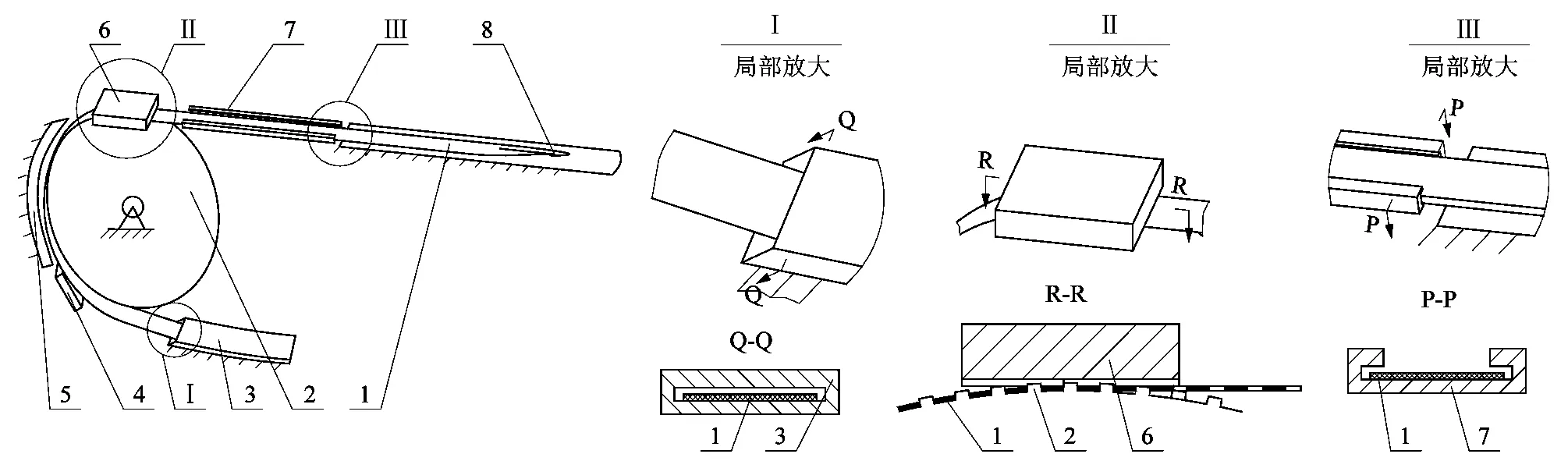
1—剑带；2—传剑轮；3—剑库；4—剑带压块；5—剑带护圈；6—剑带压块；7—静导轨；8—剑头。图1 剑带约束原理图Figure 1 Schematic diagram of rapier belt restraint

2 碳纤剑带的刚度属性

引纬过程中剑带包覆在传剑轮表面，而碳纤剑带内部均匀分布的方孔与传剑轮齿相互啮合，在传剑轮的驱动下实现引纬功能。碳纤剑带带宽30 mm，带厚t=1.35 mm，如图2所示。

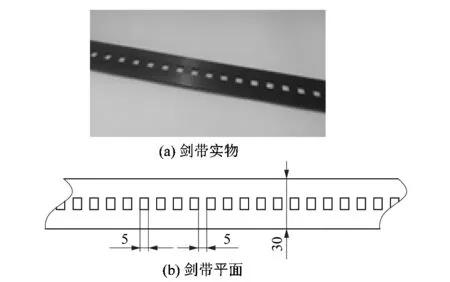
图2 碳纤剑带Figure 2 Carbon fiber rapier belt

2.1 测试刚度属性的理论模型

为研究碳纤剑带约束特征，需获得碳纤剑带刚度属性参数。基于悬臂梁力学模型，测量碳纤剑带刚度属性，如图3所示。因碳纤剑带内部质量分布不均匀(见图2)，不宜单独测量弹性模量E及惯性矩I，可将实验数据通过计算来获得剑带截面抗弯刚度参数EI。

图3 悬臂梁在集中力作用下的形变Figure 3 Deformation of cantilever beam under concentrated force

已知挠度vB为

(1)

式(1)变换可得截面抗弯刚度参数EI为

(2)

2.2 测试刚度属性的实验模型

实验如图4所示，通过增减砝码改变集中载荷F、移动剑带夹紧位置改变距离l，测得挠度值vB，计算获得剑带截面抗弯刚度参数EI。

图4 悬臂梁实验测量实物图Figure 4 Actual picture of cantilever beam experimental measurement

2.3 测试结果

碳纤剑带的截面抗弯刚度如表1所示。

表1 碳纤剑带的截面抗弯刚度EITable 1 Sectional bending stiffness EI of carbon fiber belt

综上所得，经数据处理后，剑带截面抗弯刚度EI约为0.25 N·m2。

3 碳纤剑带的约束载荷

3.1 剑带静态约束载荷

取包绕在传剑轮上的剑带为研究对象，对剑带进行静态约束载荷分析，如图5所示。

图5 剑带的静力分析Figure 5 Static analysis of rapier belt

图中：F1，F2为剑带压块对剑带的约束载荷；FN为传剑轮各齿对剑带的均布载荷。对剑带包绕传剑轮的约束载荷F1和F2进行分析(由于F1=F2，下文中均以约束载荷F代替)，探究影响约束载荷特征的因素。

3.2 约束载荷理论模型

剑带、剑带压块及传剑轮位置关系如图6所示。剑带压块对剑带起约束作用，使剑带包覆在传剑轮上，且剑带压块下表面与剑带上表面存在间隙c。

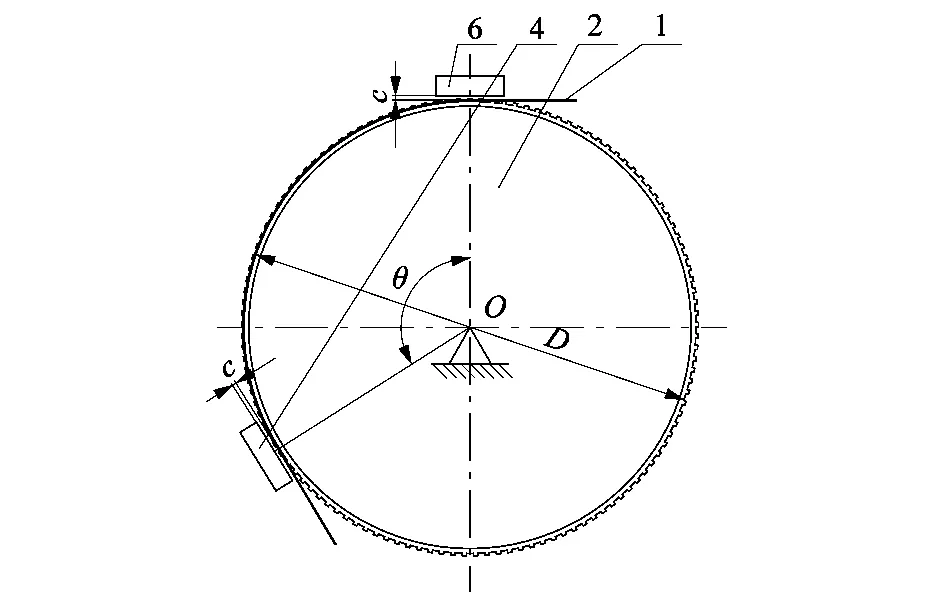
1—剑带；2—传剑轮；4—剑带压块；6—剑带压块。图6 剑带、剑带压块及传剑轮位置关系Figure 6 Positional relationship between rapier belt, pressing block and rapier wheel

图6中D为传剑轮底径，θ为剑带对传剑轮的包络角。剑带包绕传剑轮的约束载荷可近似于梁在弯曲力作用下的力学模型，如图7所示。

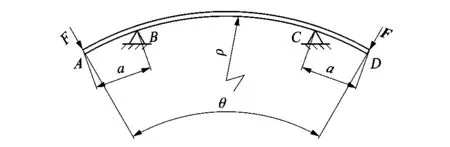
图7 梁在弯曲力作用下的变形示意图Figure 7 Schematic diagram of beam deformation under bending force

图7中a为力臂，ρ为曲率半径。取图6中剑带压块6处进行剑带弯曲变形分析，剑带包绕传剑轮的约束载荷作用支点可参考图8所示。

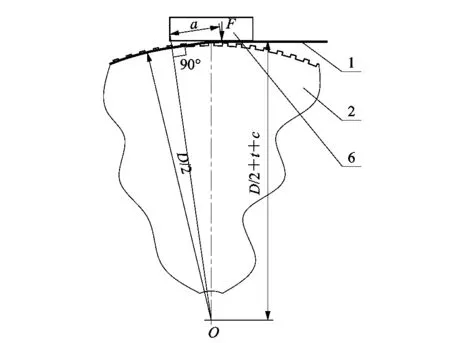
1—剑带；2—传剑轮；6—剑带压块。图8 剑带约束载荷支点示意图Figure 8 Schematic diagram of restraint load fulcrum of rapier belt

在纯弯曲情况下，弯矩与曲率间的关系为

(3)

弯矩与作用载荷关系为

M=Fa。

(4)

将图8简化，得到剑带位置示意如图9所示。

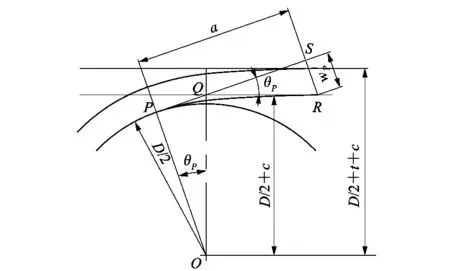
图9 剑带约束载荷支点简图Figure 9 Rapier belt restraint load fulcrum vector

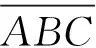
(5)

(6)

当θP足够小，tanθP≈θP，结合图9和式(5)～(6)，可得力臂a为

(7)

联立式(3)～(4)和式(7)，集中约束载荷F为

(8)

3.3 约束载荷实验

根据图7理论模型搭建图10实验平台，测得各条件下剑带的约束载荷F如表2所示。

图10 静态载荷约束实验照片Figure 10 Photo of static load restraint experiment

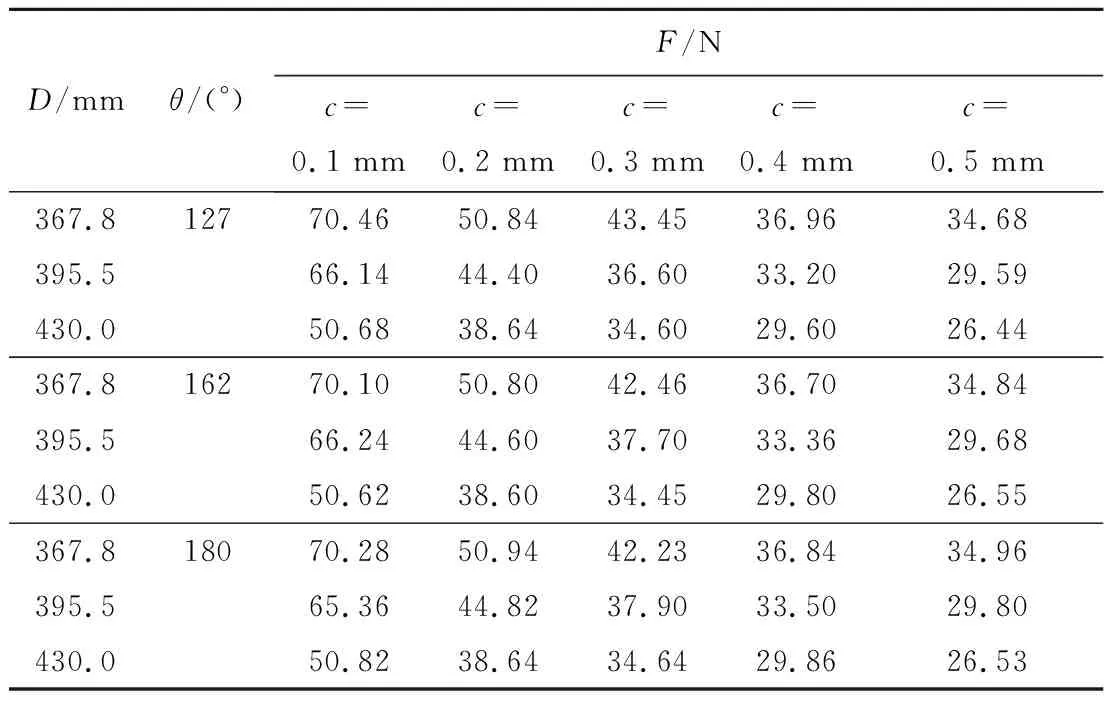
表2 实验测得不同条件下对应的约束载荷FTable 2 Experimentally measured corresponding restraint load F under different conditions

3.4 实验数据分析

由表2实验数据可知：改变传剑轮底径D，约束载荷F随之变化，底径D越大，约束载荷F越小，初步证明约束载荷F与传剑轮底径D呈负相关；改变包络角θ，约束载荷F无明显变化，即约束载荷F与包络角θ无关；剑带压块与剑带的间隙c越大，约束载荷F越小，即约束载荷F与间隙c呈负相关。根据式(8)的计算关系，F与D和c之间的变化规律如表3所示。

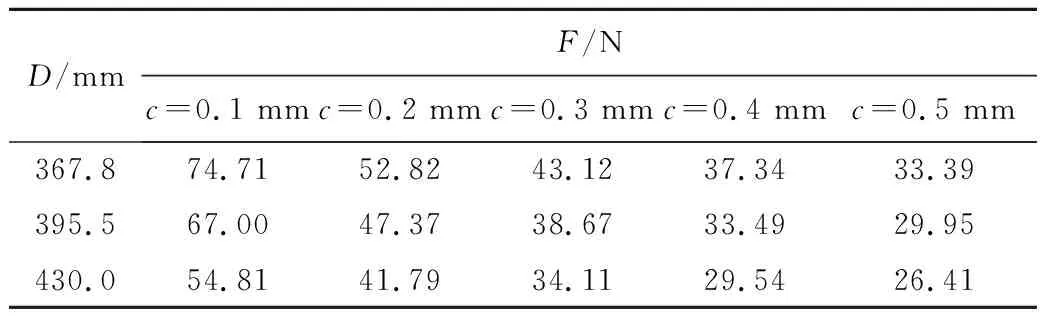
表3 剑带约束载荷F随D，c改变的理论值Table 3 Theoretical value of restraint load F of rapier belt changing with D and c

将表2实验数据与表3理论值进行对比，曲线如图11所示。可知剑带约束载荷实验数据与理论值基本吻合，验证理论模型正确，同时也得出结论：传剑轮底径D、剑带压块下表面与剑带上表面间隙c是影响剑带约束载荷的2个重要因素。

图11 数据对比Figure 11 Data comparison

4 结论

课题组针对剑杆织机碳纤剑带包绕传剑轮进行了约束载荷分析，得出影响剑带约束载荷的主要因素：

1) 传剑轮底径。底径越大，约束载荷越小。

2) 剑带压块与剑带的间隙。间隙越大，约束载荷越小。

3) 剑带截面抗弯刚度。刚度越大，约束载荷越大。

根据上述研究结论，课题组提出减小剑带约束载荷的措施：

1) 在设计时尽可能增大传剑轮底径；

2) 在设计和使用时，严格控制剑带压块与剑带的间隙；

3) 条件许可时降低剑带截面抗弯刚度。

约束载荷减小，摩擦因数不变情况下，剑带所受摩擦力减小。因此剑带在高速运动过程中摩擦产生的温升降低，剑带受热开裂分层情况得到改善，从而提高剑带的使用寿命。