一种高选择性和小通带比的三通带三维频率选择表面
于正永,陆华丽,唐万春
(1.江苏电子信息职业学院计算机与通信学院,江苏 淮安 223003)(2.南京师范大学物理科学与技术学院,江苏 南京 210023)
频率选择表面(frequency selective surface,FSS)可以应用于天线罩[1]、天线副反射器[2]、吸波体[3]以及电磁屏蔽[4]等领域. 与传统的滤波器相比[5-7],FSS是一种由具有特定形状的周期单元组成的二维阵列结构,具有独特的空间滤波特性,可以实现带通或带阻滤波性能. 在卫星通信系统中,为了增加多频天线的通信能力,要求FSS能够工作在相应的多个频段. 同时,当3个通信通道工作在相近的频率时,此时需要设计具有小通带比的三通带FSS.
为了满足上述的应用需求,一些三通带FSS被研究人员提出. 通过集总元件加载[8]、盘绕结构[9]和互补结构[10]等方式,提出了3种相似频率响应的三通带FSS. 但是,这3种FSS每个通带均为一阶响应,由于缺少传输零极点,存在通带不够平坦和带外抑制宽度较窄等不足. 通过堆叠三层方环阵列,设计了一种具有高选择性和良好角度稳定性的三通带FSS[11]. 最近,研究人员通过将文献[11]中的方环替换为六边形环,拓宽了第二通带的工作带宽,降低了带内的插入损耗[12]. 但是,这两种FSS[11-12]的第一通带仍为一阶响应;同时随着入射角度的增加,在高频段均出现了栅瓣效应. 作为一种替换的方法,三维(three-dimensional,3D)FSS的概念被提出[13-15]. 其中,文献[13]基于阶梯阻抗和均匀阻抗两种谐振结构,采用多层印刷电路板(printed circuit board,PCB)技术实现了一种具有二阶响应的三通带FSS,但是,该3D FSS仅能够工作在单极化模式,而且带外没有任何传输零点,其频率选择性能一般. 通过上下两层加载不同大小的圆形金属贴片,中间层加载圆形孔径,借助孔径电磁耦合,实现了一种双极化、二阶三通带FSS[16],不过,其带外也未引入任何传输零点,其频率选择性能需要进一步提升,同时由于单元结构的电尺寸很大,导致了其角度稳定性较差. 此外,以上文献所提出的三通带FSS相邻通带的通带比多数较大,在一定程度上限制了其实际应用.
本文基于微波滤波器等效电路拓扑,设计了一种高选择性、小通带比的三通带3D FSS. 由于该3D FSS单元结构具有对称性,因此,很容易实现双极化功能. 当以0°、30°和60°角度入射时,该3D FSS具有稳定的频率响应.
1 FSS单元设计与仿真
1.1 微波滤波器等效电路拓扑
图1给出了一阶三通带微波滤波器的等效电路拓扑,该拓扑由电感L0与三个并联的LC(L1-C1,L2-C2,L3-C3)串联谐振器组成.
当电感L0与L1-C1串联谐振器同时谐振时,会产生1个传输零点fz1和一个传输极点fp1(fz1>fp1).如下:
(1)
(2)
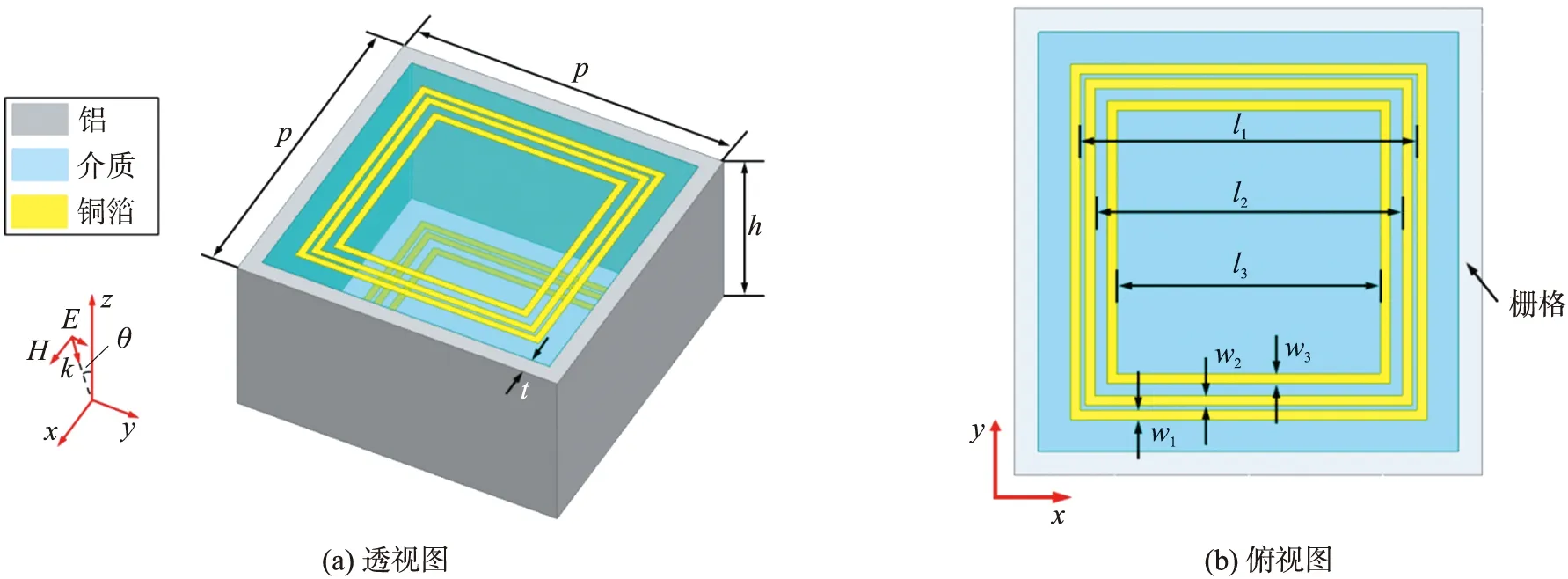
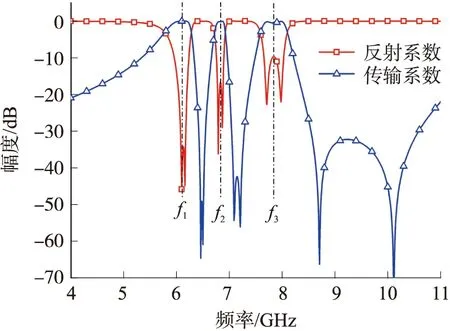
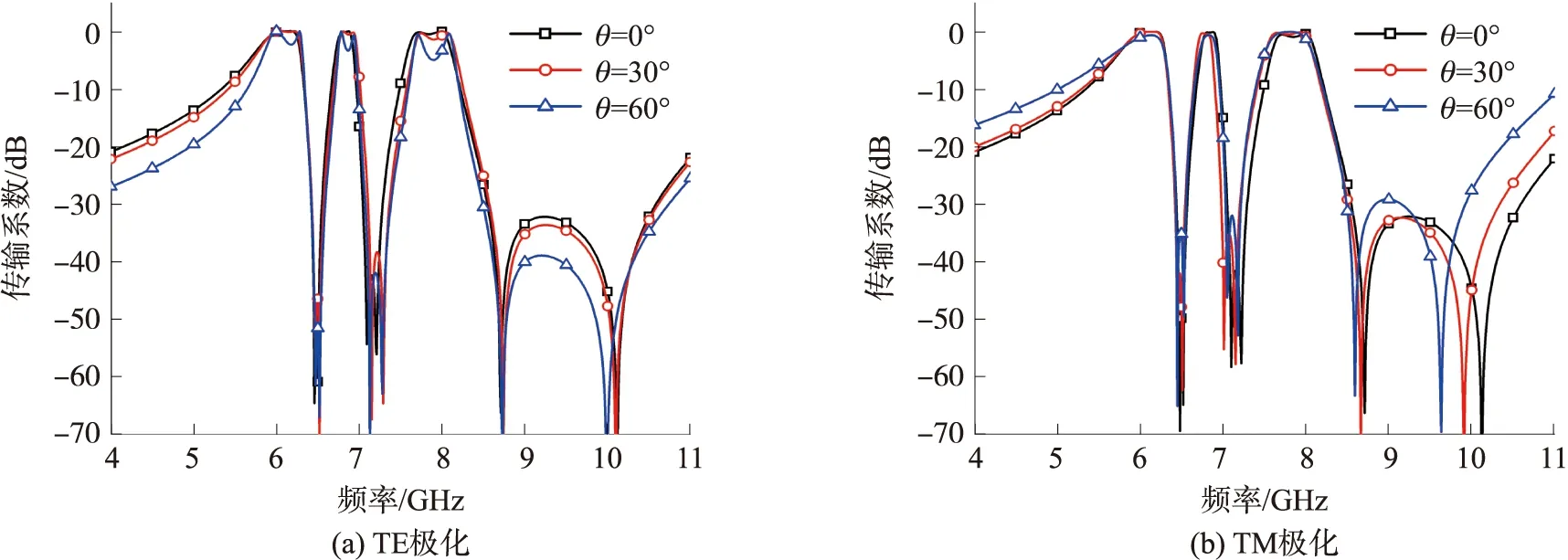
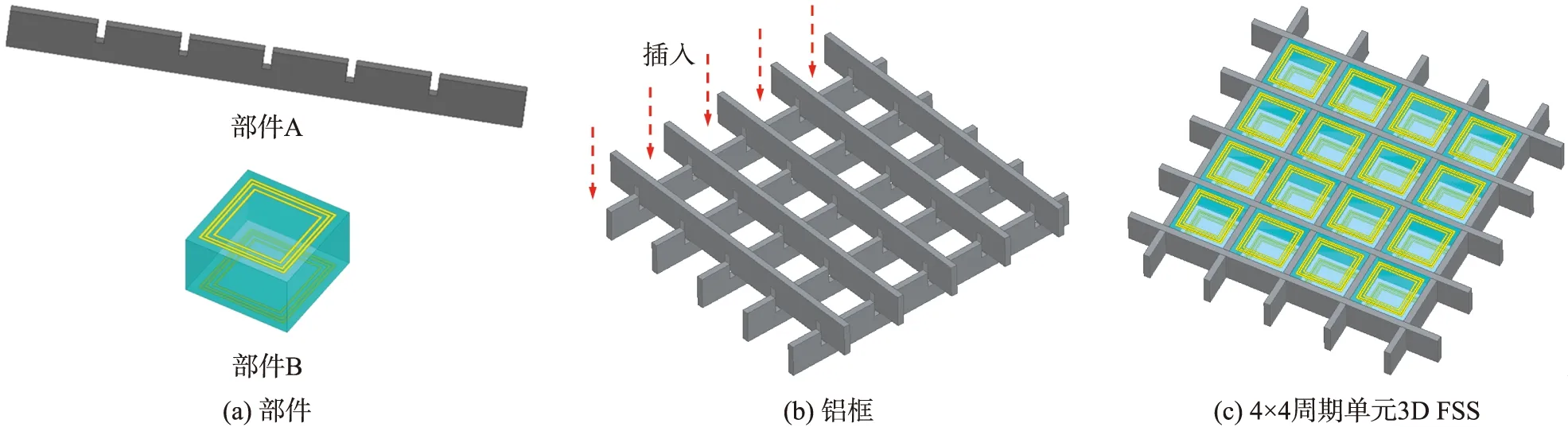
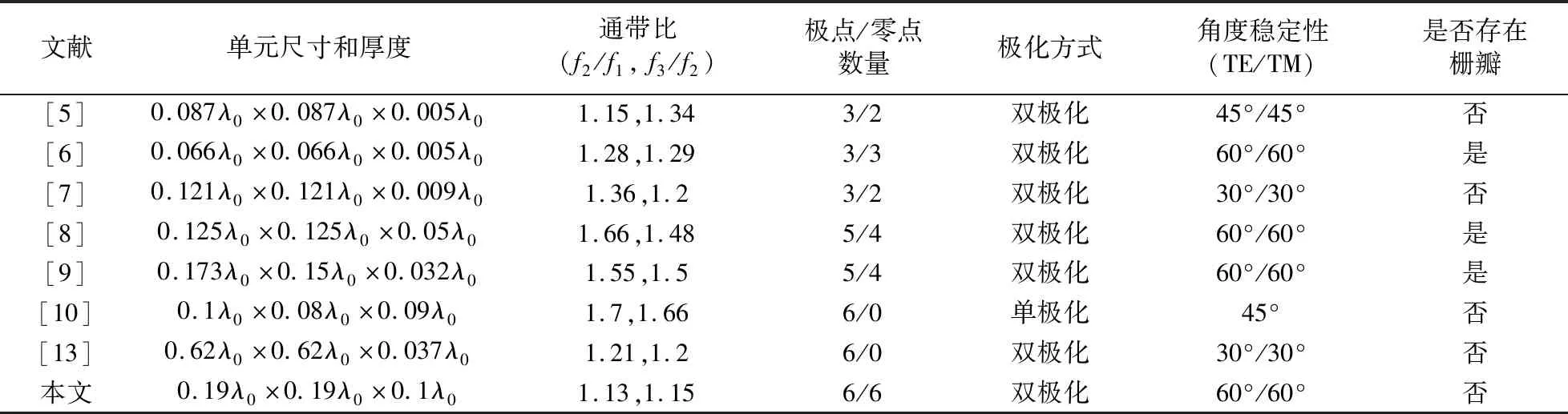
当L2-C2串联谐振器发生谐振时,可以产生第二个传输零点fz2(fz2>fz1).根据文献[17]可知,两个相邻LC串联支路的并联会在两个传输零点之间产生1个传输极点,由此产生了第二个传输极点fp2(fz1 (3) (4) 同理,当L3-C3串联谐振器发生谐振时,可以产生第三个传输零点fz3(fz3>fz2)和第三个传输极点fp3(fz2 (5) (6) 综上所述,当图1中所有谐振器同时工作时,可以在fp1、fp2、fp3附近产生了3个通带,同时在fz1、fz2、fz3附近产生了3个阻带.但是,可以发现,每个通带仅包含1个传输极点,每个阻带仅包含1个传输零点,因此,很难形成平坦的通带和较宽的带外抑制.针对这个问题,将图1的电路拓扑进行了双层堆叠,并使用传输线进行连接,构建二阶三通带微波滤波器等效电路拓扑,如图2所示.此时,在电磁耦合作用下,原有单一的谐振模式(fp1、fp2、fp3、fz1、fz2、fz3)耦合分裂为奇模和偶模两种模式,因此,该拓扑能实现3个二阶通带和3个二阶的阻带. 图1 一阶三通带微波滤波器等效电路拓扑Fig.1 Topology of the first-order tri-band bandpass microwave filter 图2 二阶三通带微波滤波器等效电路拓扑Fig.2 Topology of the second-order tri-band bandpass microwave filter 众所周知,FSS本质上是一种空间微波滤波器,因此,图2所示的二阶三通带微波滤波器等效电路拓扑可以用来设计二阶三通带FSS. 依据文献[18-19]中等效电路分析可知,栅格结构可以等效为电感,方环阵列可以等效为LC串联谐振器,传输线用方波导传输线来代替,因此,得到了所设计的二阶三通带3D FSS的单元结构示意图如图3所示.由图3可知,每个单元结构由1个空气方波导和1个上下端面均刻蚀3个同心方环的介质方块组合而成.单元结构在x和y轴方向上周期尺寸均为p,栅格的宽度为t,从外到内3个方环的内边长和线宽分别为l1和w1、l2和w2、l3和w3,FSS的厚度为h.此外,介质方块的相对介电常数为εr. 图3 三通带3D FSS单元结构Fig.3 Unit cell of tri-passband 3D FSS 针对高选择性、小通带比、低插入损耗等FSS指标的设计目标,FSS相应的物理尺寸可以通过多次优化设计后得到,如表1所示. 在此基础上,可以运用文献[18-19]中相关公式计算图2中各个电参数,但是由于单元结构中存在的电磁耦合较为复杂,因此,这些计算公式并不能给出电参数的准确值,只能给出电参数的初始值,电参数的最终值可以通过曲线拟合方法获得[20]. 表1 三通带3D FSS的设计参数Table 1 Design parameters of tri-passband 3D FSS 图4给出了设计参数如表1所示的三通带3D FSS的传输系数和反射系数的HFSS软件仿真结果. 由图可以看出,该3D FSS在f1=6.03 GHz、f2=6.82 GHz、f3=7.845 GHz中心频率处实现了3个二阶平坦通带,其中,第一通带包含6.1 GHz和6.16 GHz两个传输极点,第二通带包含6.79 GHz和6.87 GHz两个传输极点,第三通带包含7.71 GHz和7.98 GHz两个传输极点. 同时,在第一通带与第二通带之间引入了6.46 GHz和6.5 GHz两个传输零点,在第二通带与第三通带之间引入了7.09 GHz和7.21 GHz两个传输零点,此外在第三通带右侧带外引入了8.71 GHz和10.11 GHz两个传输零点,使得该FSS具有较好的频率选择性能. 此外,由于方波导腔的高Q值,其频率选择性能得到了进一步提高. 在第三通带右侧得到了1个工作带宽约为43%的宽阻带. 该FSS 3个通带的3dB带宽分别为0.5 GHz(5.78~6.28 GHz)、0.2 GHz(6.72~6.92 GHz)和0.51 GHz(7.59~8.1 GHz),对应的相对带宽分别为8.29%、3.32%和8.46%. 该3D FSS单元结构的电尺寸为0.19λ0×0.19λ0×0.1λ0,其中λ0为第一通带中心频率f1处自由空间波长. 由于3个尺寸十分接近的同心方环设计,使得该3D FSS相邻通带之间的间距很小,第二通带与第一通带、第三通带与第二通带之间的通带比分别仅为f2/f1=1.13和f3/f2=1.15. 图4 三通带3D FSS传输系数和反射系数的HFSS软件仿真结果Fig.4 Simulated transmission and reflection coefficients of tri-passband 3D FSS by HFSS 为了进一步弄清该3D FSS的工作原理,对传输极点处的表面电流分布进行了研究,如图5所示. 由图5(a)和5(b)可以看出,传输极点fp1和fp2处的表面电流主要分布在上下端面的最外层方环和栅格上,这表明fp1和fp2是由最外层方环和栅格共同影响的. 由图5(c)和5(d)可知,传输极点fp3和fp4的表面电流主要集中在上下端面的最外层方环和中间层方环上,这表明fp3和fp4是由这两个方环共同产生的. 如图5(e)和5(f)所示,传输极点fp5和fp6的表面电流主要分布在上下端面的中间层方环和最内层方环上,这表明fp5和fp6是由这两个方环共同提供的. 很显然,以上所得的分析结果与上述等效电路拓扑的传输极点产生机理是一致的. 图5 传输极点处的表面电流分布Fig.5 Surface current distributions at transmission-pole frequencies 由于所设计的三通带3D FSS结构具有对称性,因此,该FSS可以实现双极化. 图6给出了该FSS在TE和TM两种极化模式下的频率响应,由图可以看出,在这两种极化模式下该FSS具有相同的频率响应,这充分说明该FSS具有双极化性能. 图6 TE和TM两种极化模式下该3D FSS的频率响应Fig.6 Frequency responses of the 3D FSS under TE and TM polarization modes 运用HFSS软件仿真得到了该3D FSS在不同极化模式和不同入射角度条件下的传输系数,如图7所示. 由图7可以发现,该FSS在TE和TM极化模式下以0°,30°,60°角度入射时具有稳定的频率响应. 如图7(a)所示,对于TE极化模式,随着入射角度的增加,3个通带内的插入损耗随之增加,主要原因在于当入射角θ增大时,其端口的波阻抗ZTE=Z0/cosθ[21]将会随之增大. 此外,通常一个较大的波阻抗将会导致该FSS内的谐振器具有较高的品质因数,从而使得通带的带宽在TE极化工作模式下减小. 如图7(b)所示,对于TM极化模式,当入射角θ增大时,其端口的波阻抗ZTM=Z0cosθ[21]将会随之减小,将会导致该FSS内的谐振器具有较低的品质因数,从而使得通带的带宽增大. 也可以看出,在TM极化模式下,通带的插入损耗受入射角度变化的影响不大. 图7 不同入射角度下该3D FSS传输系数仿真结果Fig.7 Simulated transmission coefficients of 3D FSS under oblique incidence for(a)TE polarization;(b)TM polarization 所提出的3D FSS实物可以通过机械加工线切割和PCB两种方法来实现. 以4×4(16个)周期单元3D FSS为例,其部件加工和组装的步骤如图8所示,具体来说:(1)采用线切割方法加工厚度为2t=1 mm的长条型铝板,并在其表面周期性地开凿5个矩形方槽(宽度为2t=1 mm,高度为h/2=2.5 mm),从而形成部件A;采用印刷电路PCB加工方法制作上下端面均刻蚀3个同心方环的介质方块,从而形成部件B. 如图8(a)所示. (2)将10个部件A通过交叉对插方式构成一个铝框,形成16个周期性的空气方波导结构,如图8(b)所示. (3)将16个部件B逐一插入到铝框的16个方波导结构中,最终组合为所提出的3D FSS实物,如图8(c)所示. 通常运用自由空间测量法[22]对所制作的3D FSS实物进行实验测试. 首先测试出未放置FSS情况下的传输系数,以便去除传输损耗带来的影响,其次测试出放置FSS情况下的传输系数,然后再测试出FSS替换为相同尺寸的金属板时的传输系数,以便去除周围环境噪声带来的影响,最后,运用矢量网络分析仪的时域门函数对测量结果进行校准,以便考虑多路径传输带来的影响. 图8 FSS实物加工及组装Fig.8 Fabrication and assembly of the FSS prototype 表2给出了所提出的3D FSS与现有相似特性的FSS的性能对比. 从表不难看出,所提出的3D FSS具有高选择性、小通带比、良好的角度稳定性、双极化以及无栅瓣产生等优势. 表2 与现有相似特性的FSS的对比Table 2 Comparison of the FSS designs with similar characteristic 从微波滤波器等效电路拓扑出发,提出了1种FSS设计方法,由此实现了1种具有高选择性和小通带比的二阶三通带3D FSS. 借助上下端面谐振单元之间的电磁耦合,引入了多个传输零极点,提高了其频率选择性能,同时,方波导腔的高Q值进一步增强了频率选择性能. 通过3个尺寸十分接近的方环设计,实现了相邻通带之间的小通带比设计. 通过分析传输极点处的表面电流分布,阐明了该FSS的工作原理. 同时,阐述了所提出的3D FSS实物的加工和测量方法. 仿真结果表明:该3D FSS具有高选择性、小通带比、良好的角度稳定性、双极化以及无栅瓣产生等优势.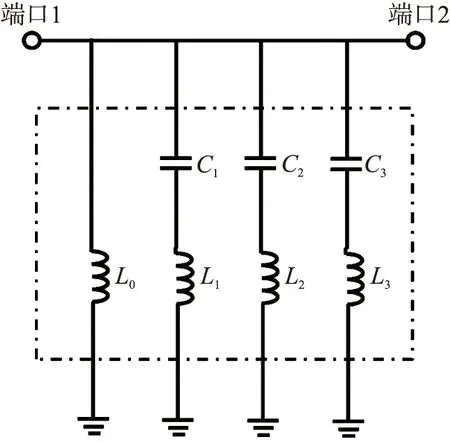
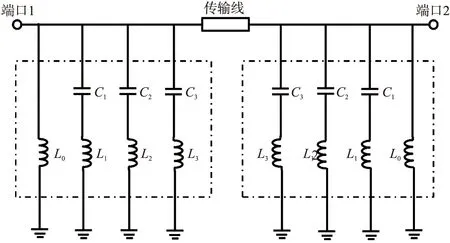
1.2 周期单元结构与滤波响应

1.3 传输极点处的表面电流分布

2 FSS极化独立性和角度稳定性

3 实物加工和测量方法
4 结果与讨论
5 结论

