等和线在平面向量中的应用

刘春

摘要：向量是既有大小又有方向的量，它是数与形的完美结合.因此，我们可以向量为工具，研究相关数学问题.像利用平面向量基本定理，研究两系数的和、差及线性表达式的范围与最值等问题，最为常见.学生在处理此类问题时，往往通过建立直角坐标系或者利用角度关系与数量积公式来处理，但其解题过程较为繁琐.利用平面向量等和线，能快速有效地解答问题。

关键词： 等和线;最值;原理;性质

一、等和线概述

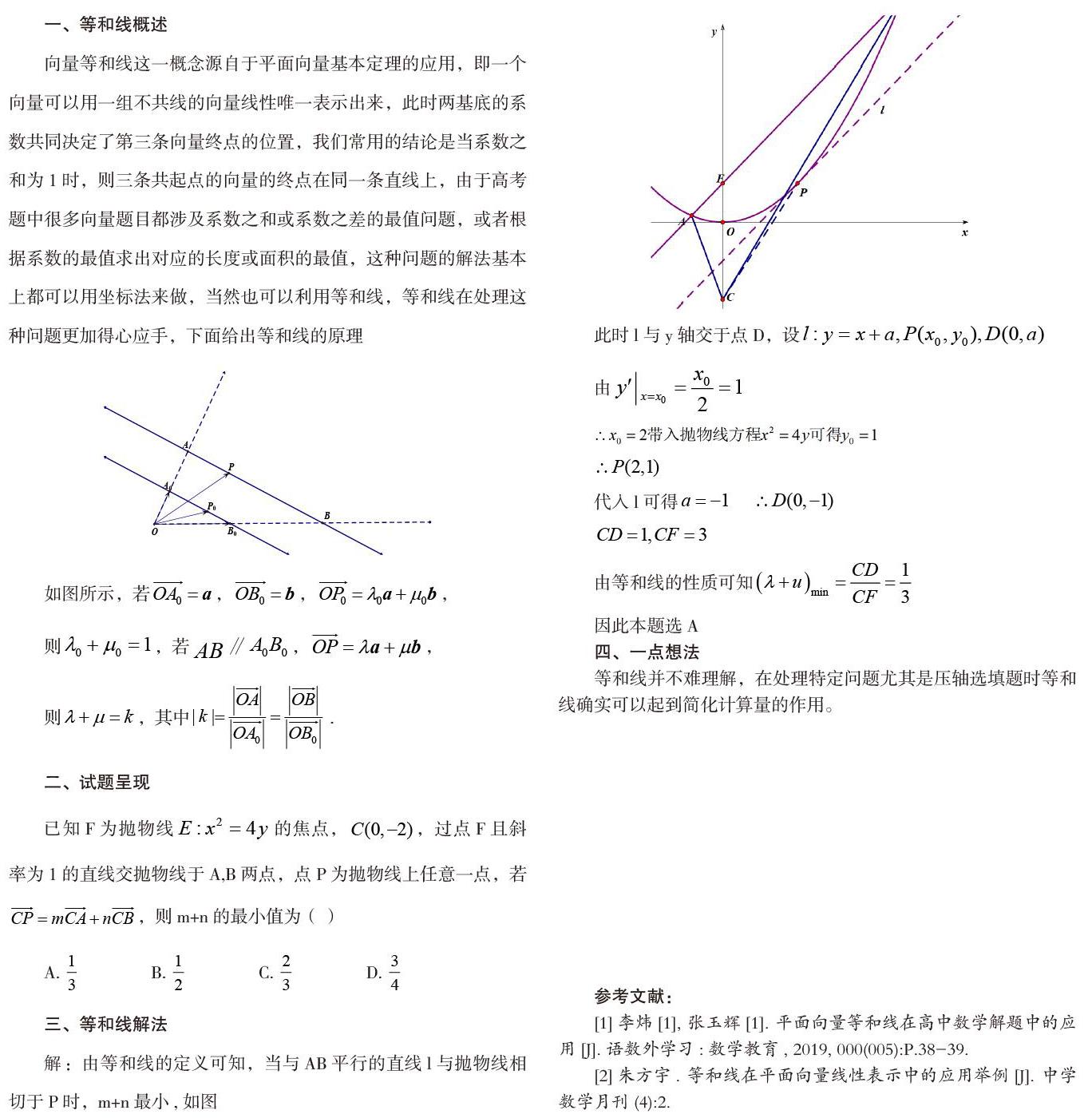
向量等和线这一概念源自于平面向量基本定理的应用，即一个向量可以用一组不共线的向量线性唯一表示出来，此时两基底的系数共同决定了第三条向量终点的位置，我们常用的结论是當系数之和为1时，则三条共起点的向量的终点在同一条直线上，由于高考题中很多向量题目都涉及系数之和或系数之差的最值问题，或者根据系数的最值求出对应的长度或面积的最值，这种问题的解法基本上都可以用坐标法来做，当然也可以利用等和线，等和线在处理这种问题更加得心应手，下面给出等和线的原理

参考文献：

[1]李炜[1]， 张玉辉[1]. 平面向量等和线在高中数学解题中的应用[J]. 语数外学习：数学教育， 2019， 000（005）：P.38-39.

[2]朱方宇. 等和线在平面向量线性表示中的应用举例[J]. 中学数学月刊（4）：2.