大跨度门式干煤棚网壳结构整体稳定性能分析

方志庆，李长春，干梦军

（1. 中国电力工程顾问集团华东电力设计院有限公司，上海 200063；2. 安徽淮南洛能发电有限责任公司，安徽 淮南 232008）

0 引言

近年来，为了进一步加强空气污染防治、有效改善环境空气质量，相关部门陆续出台了一系列环境保护政策。其中，规定储煤场应采用筒仓、条形或者圆形封闭形式，因此需要将大量原有的露天煤炭储存转换为封闭式煤炭储存，而干煤棚结构也逐步在实际工程中得到了推广和应用[1]。

由于大跨度空间结构的自身特点，稳定成为大跨度干煤棚设计领域中的重中之重。例如门式干煤棚网壳结构，该结构跨度大、矢跨比小，存在整体失稳或局部失稳发生的可能性，在杆件应力比计算的基础下，进行结构整体稳定的计算，评估结构的整体稳定性能是该类结构设计的重要环节之一。

网壳的稳定性可按考虑几何非线性的有限元法（即荷载—位移全过程分析）进行计算，分析中可假定材料为弹性，也可考虑材料的弹塑性。对于大型和形状复杂的网壳结构宜采用考虑材料弹塑性的全过程分析方法[2]。本文基于某门式干煤棚网壳结构的整体稳定性分析，主要包括特征值屈曲分析和非线性稳定分析，其中通过引入初始几何缺陷进行非线性分析，研究不同初始几何缺陷下位移—荷载曲线变化形态，并比较整体结构的极限承载力的差异，为类似的实际工程提供参考和建议。本文中的门式干煤棚网壳结构体型尺寸适中，并且结构外形和荷载均大致对称，故假定材料为弹性，不考虑材料的弹塑性。

1 工程概况

某干煤棚纵向长度160 m，跨度114 m，最高高度约为43 m，可以覆盖两个煤场。由于煤场内采用门式斗轮机，故干煤棚采取门式网壳结构外形设计予以匹配，干煤棚剖面图如图1所示。

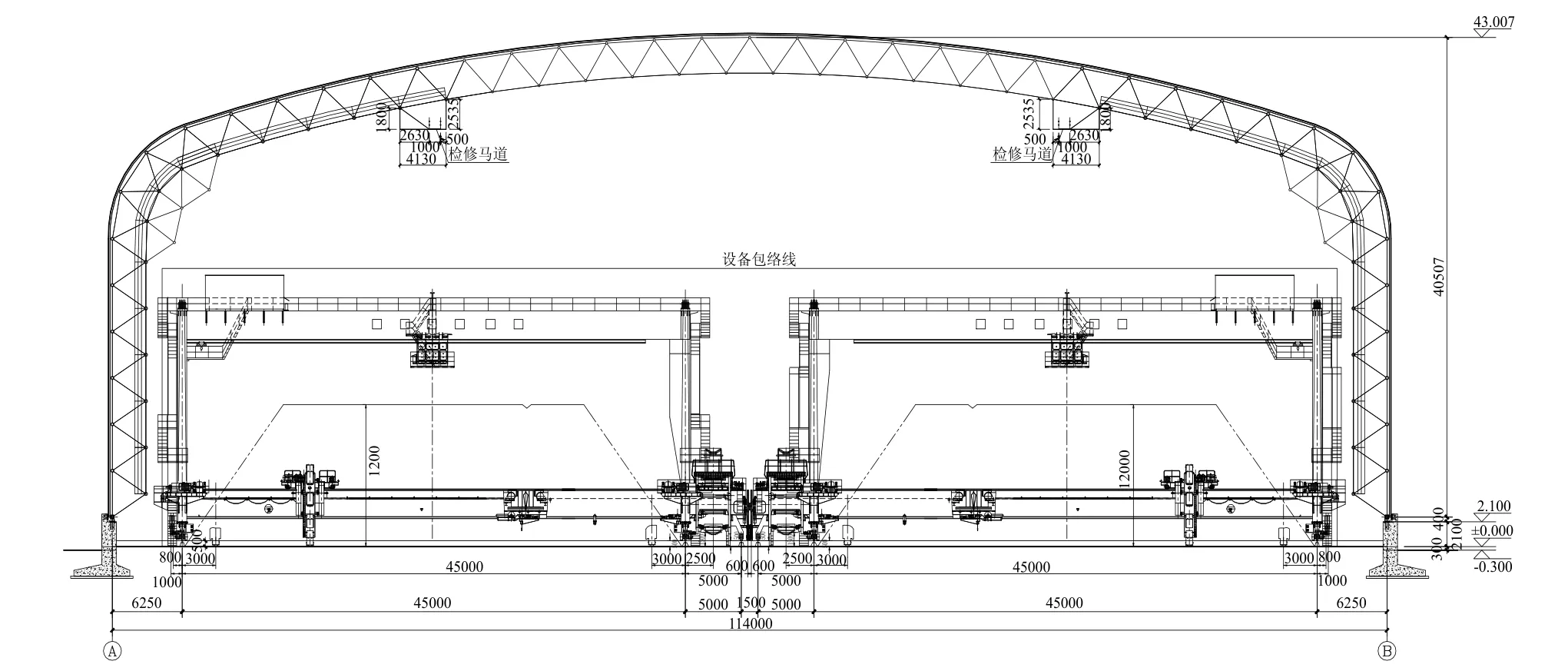
图1 干煤棚剖面图

本门式网壳结构设计使用年限为50 a；结构安全等级为二级；抗震设防烈度为7度，设计基本地震加速度0.10 g，设计地震分组为第一组，建筑场地类别为Ⅱ类；地面粗糙度为B类。主要的荷载取值如表1所示。

表1 结构主要荷载取值

本门式网壳结构采用MIDAS GEN软件建立了三维有限元分析模型，结构计算分析模型示意图，如图2所示，直段和曲线段交接处应力较大采用三层网壳，其他区域为双层网壳，网架厚度为3 m，支座为铰接，纵向支座间距为8 m，杆件采用桁架单元。

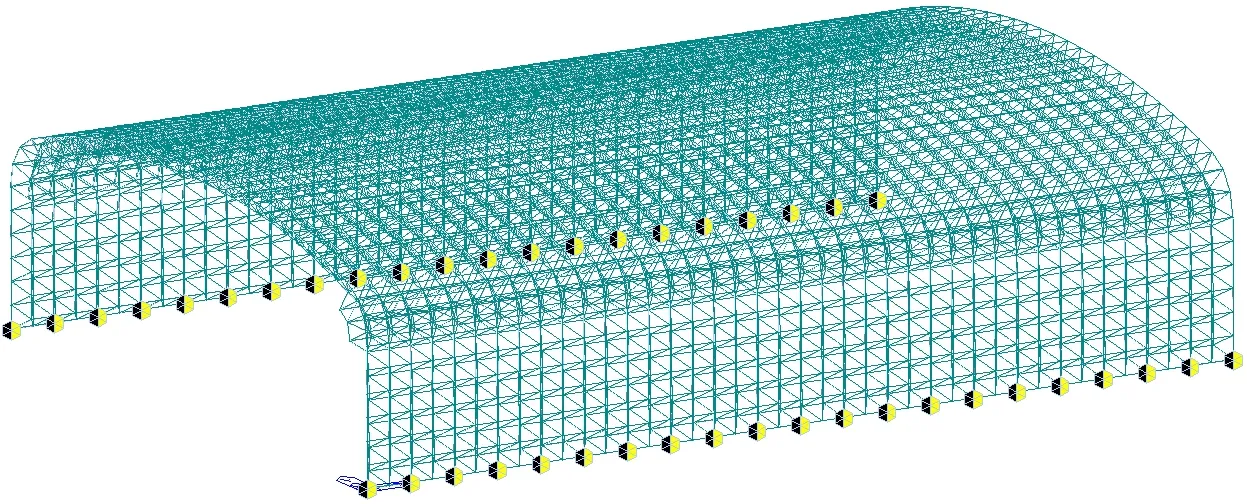
图2 结构计算分析模型

2 结构特征值屈曲分析

特征值屈曲分析属于线性分析，虽然和实际工程不相符，但仍可以从结构特征值屈曲分析中得到结构稳定的基本特征，为非线性分析奠定基础，起到初步评估的作用[2]。

根据JGJ 7—2010《空间网格结构技术规程》[3]规定要求，本网壳结构特征值屈曲分析采用的荷载组合如表2所示，提取模型中前20阶屈曲因子，选取结构的最不利荷载工况组合进行计算和分析。不同荷载组合中的荷载加载示意图，如图3～图6所示。

表2 结构荷载组合表

图3 1.0恒载加载示意图

图4 1.0满跨活载加载示意图

图5 1.0活载工况1（右半跨满跨）加载示意图

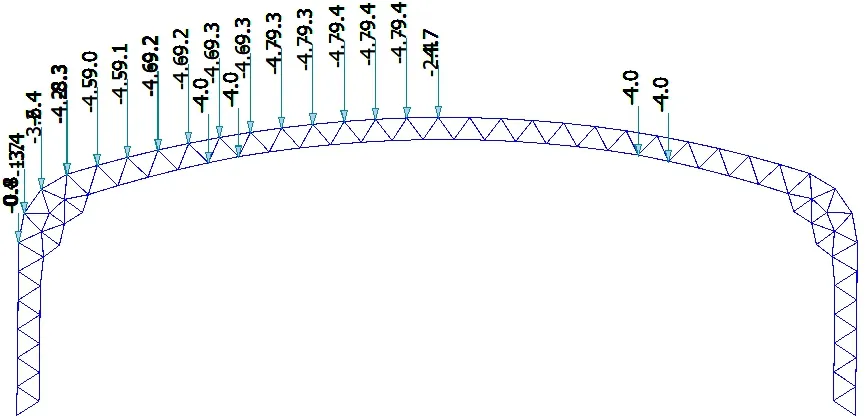
图6 1.0活载工况2（左半跨满跨）加载示意图

如表3所示，荷载工况组合1（1.0恒载+1.0满跨活载）的屈曲因子最小，安全储备较小，是网壳结构特征值屈曲分析时的最不利情况，故选荷载组合1对结构进行线性屈曲分析及后续的几何非线性稳定分析。

表3 各荷载组合下结构的前20阶屈曲因子

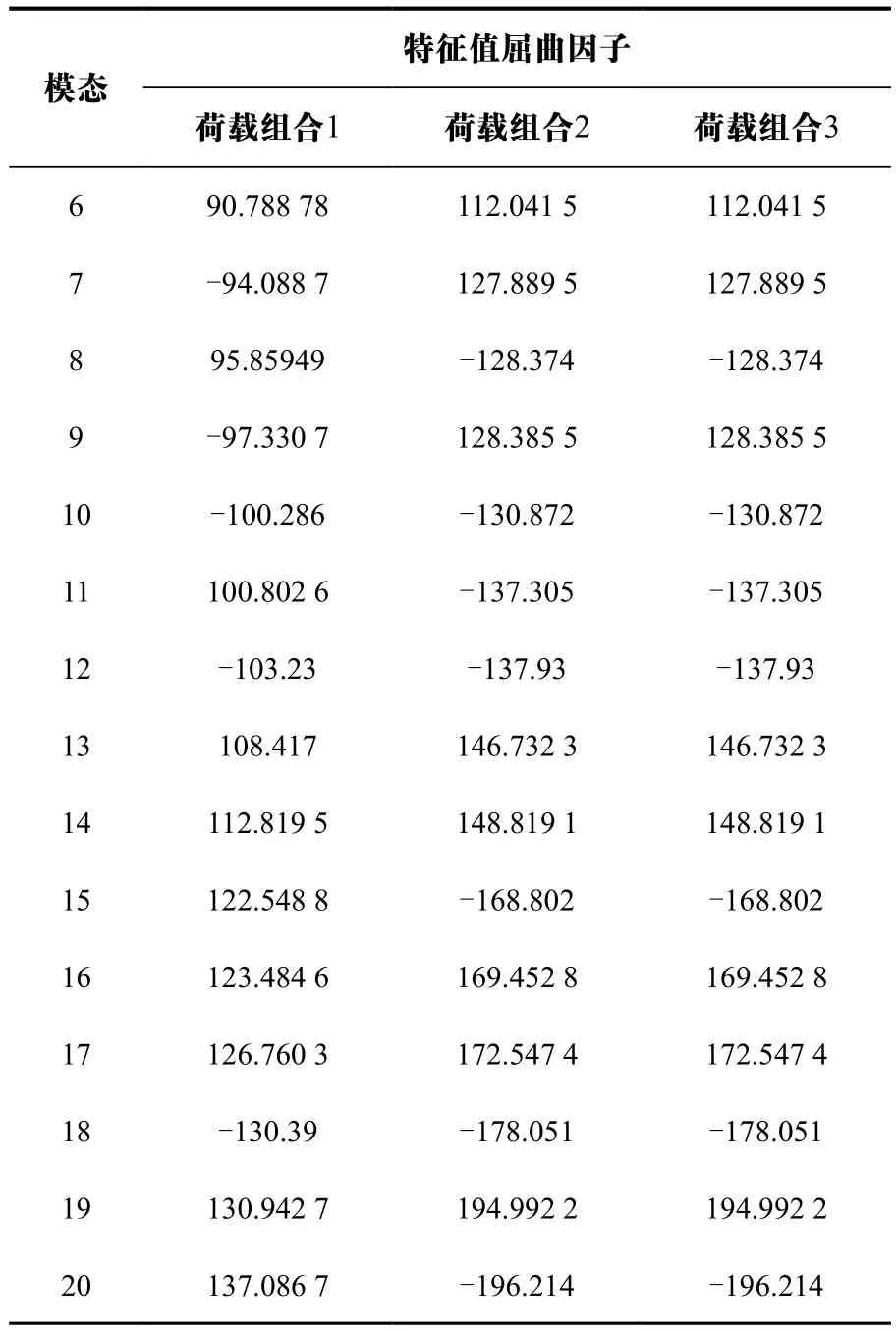
续表

计算分析得到的结构荷载组合1（1.0恒载+1.0满跨活载）的典型的屈曲模态图，如图7～图10所示。

图7 第1阶屈曲模态

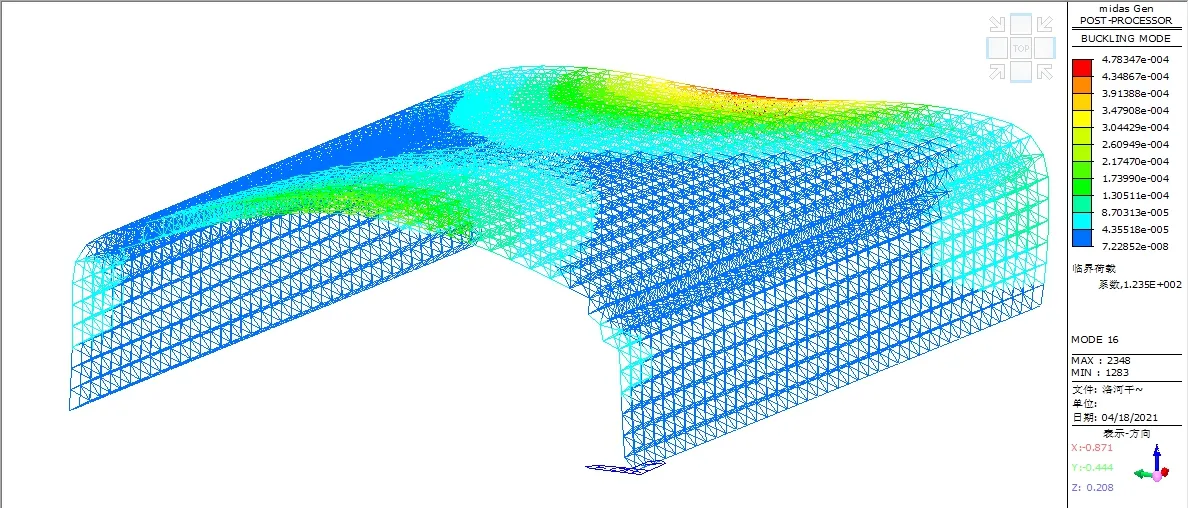
图8 第16阶屈曲模态

图9 第19阶屈曲模态

图10 第20阶屈曲模态

3 结构几何非线性分析

干煤棚网壳结构在加工制作、运输和现场安装过程中，不可避免地存在不同程度的初始几何缺陷[4-5]，故进行网壳全过程分析时应考虑初始几何缺陷的影响，初始几何缺陷分布可采用结构的最低阶屈曲模态，其缺陷最大计算值可参照JGJ 7—2010《空间网格结构技术规程》的规定，取值为网壳跨度的1/300，对于本网壳的结构，即380 mm。

为了研究不同初始几何缺陷下的荷载—位移曲线的形态以及结构极限承载力的差别，分别建立不同初始几何缺陷下的计算分析模型，其各自对应的荷载—位移曲线，如图11所示。其中荷载系数为网壳结构稳定极限承载力除以荷载取标准值（1.0恒载+1.0活载工况1），L为网壳跨度。

图11 不同初始几何缺陷情况下的荷载—位移曲线

由图11可见，不同初始几何缺陷下的结构荷载—位移曲线总的形态基本一致，该曲线大致可分为三段：①在荷载加载的初期阶段，荷载及位移值都相对较小，两者之间基本呈现线性变化的状态，而且位移增加的同时，荷载增大的速率也较快；②荷载—位移曲线两者之间仍基本呈现线性变化的状态，但荷载随着位移增加而增大的速率相比第一阶段有所减缓；③荷载—位移曲线由初始的线性逐渐转化为曲线，非线性的形态逐渐显现，当位移值达到某值时，荷载值达到第一个临界点处的荷载值，且随着位移的增加荷载突然减小，该突变点对应的荷载值为结构的临界荷载，此时结构开始失稳。

不同初始几何缺陷情况下，结构失稳时的变形形态基本一致，和结构特征值屈曲分析时的第1阶屈曲模态相似，均为网壳结构平面内失稳，如图12所示。

图12 结构整体失稳变形形态（初始几何缺陷为L/300）

如表4所示，比较了不同初始几何缺陷情况下荷载系数，从表中可见：①初始随着初始几何缺陷的增大，相应结构的荷载系数逐渐减小。相比无初始缺陷的结构，初始缺陷为L/500、L/300和L/200的荷载荷载系数分别减小了约3.34%、4.81%和9.73%，可见本网壳结构的非线性对网架的整体稳定性能的影响不可忽视；②初始几何缺陷取为网壳跨度的1/300时，结构的荷载系数为16.24。

表4 不同初始几何缺陷情况下荷载系数

4 结语

本文以114 m跨门式干煤棚网壳结构为研究对象，分别建立了考虑不同初始几何缺陷下结构模型，经过计算分析和研究得出：

1）满跨活荷载分布下结构的屈曲因子最小；

2）不同初始几何缺陷情况下的结构荷载—位移曲线总的形态基本一致，随着施加位移的增大，荷载—位移曲线的非线性形态逐渐显现；不同初始几何缺陷情况下，结构失稳时的变形形态基本一致，都为网壳结构平面内失稳；

3）初始随着初始几何缺陷的增大，相应结构的荷载系数均有不同程度的减小；

4）结构的非线性对网架的整体稳定性能的影响不可忽视，实际结构设计过程中应予以重视；

5）对于大跨度门式网架，建议在直段和曲线段交接处应力较大处，采用三层网壳予以加强。