基于GAMLSS模型的不同收入群体边际消费倾向研究
王 超 张 雨 滕 婵 冯钰雯
(安阳师范学院 数学与统计学院,河南 安阳 455000)
一、引言
边际消费倾向研究的核心问题之一是消费函数的设定。多数研究设定采用线性回归的设定形式(胡静娴,2010;陈训波和周伟,2013)[1][2]。线性回归模型通常以误差项服从正态分布为假定前提,也就意味着消费水平服从正态分布。而现实情况是,居民消费水平可能并不服从正态分布。金春雨和程浩等绘制了中国各省农村居民人均消费核密度图,发现中国各省农村居民人均消费呈现典型的右偏特征[3]。这就意味着,如果采用默认的正态分布进行参数拟合势必会与现实情况产生较大不适。为此,学术界尝试改变传统的模型设定形式以适应这种情形。
部分研究将非参数回归技术引入居民消费边际倾向研究之中(龙健颜和卢素等,2011;黄金波和李仲飞,2014;钱明辉和胡日东等,2018;赵卫亚,2005)[4][5][6][7]。非参数回归不需要模型满足线性的假设前提,即不需要事先假定消费水平服从正态分布,因而可以灵活地探测数据间的复杂关系。但该模型设定有一种天然不足,就是当模型中自变量数目较多时,模型的估计方差会加大,导致回归系数的估计准确度很差。另外,非参数回归中自变量与因变量间关系的解释也有难度。所以,多数使用非参数回归技术的研究仅仅是将居民收入作为影响居民消费水平的唯一因素。
为了解决这一问题,部分研究采用了半参数回归技术研究居民边际消费倾向(娄峰和李雪松,2009;田凤平和周先波等,2013)[8][9]。这种设定形式介于参数设定与非参数设定之间,即对影响居民消费的部分变量采用线性设定形式,部分变量采用非参数设定形式。由于该设定形式需要使用最小二乘法估计线性设定变量的参数,也意味着居民消费水平满足正态性的假定,从逻辑上讲,这种设定形式依然与现实不符。
首次考虑被研究现象统计分布特征的理论回归模型当属广义线性模型(Generalized Linear Model,GLM),该模型假定待研究现象(如消费)服从指数型分布。该模型并非直接在解释变量与被解释变量之间建立联系,而是通过连接函数在两者之间建立联系。连接函数的形式依被解释变量所属具体分布函数进行确定。当指数型分布为正态分布时,被解释变量的期望正好为连接函数,此时该设定与普通的线性回归模型是一致的。这意味着连续响应的普通回归模型是广义线性模型的特殊情形。由于该类模型的前提条件为指数型分布,理论上只有某些特殊的情形才满足这一条件。如对右偏型数据进行分析时,由于存在较少数量的右偏性质的指数型分布,所以这种模型在居民边际消费倾向研究中使用较少。
为了使模型设定更加灵活,以揭示自变量的非线性效应,将非参数设定形式的自变量引入就成为广义线性模型的一种自然扩展。这种扩展被称为广义可加模型(Generalized Additive Models,GAM),该模型由Hastie和Tibshirani于1990年提出。由于遵循了广义线性模型的理论框架,因此广义可加模型也需要因变量服从指数族分布形态,极大地限制了其他非指数族分布现象的建模,客观上为该模型的扩展提供了潜在可能。2005年,Rigby和Stasinopoulos提出了包含位置、规模和形状的广义可加模型(Generalized Additive Models for Location,Scale,and Shape,GAMLSS),很好地解决了非指数族分布现象的建模问题[10]。
经过文献梳理,发现现有关于居民家庭边际消费倾向的研究多集中于线性模型的设定形式,且以被解释变量服从正态分布为假设前提条件,鲜有文献集中于消费分布的探讨。本文针对以往研究存在的不足,从以下三个方面进行改进。
第一,普通线性回归模型的设定形式并不能客观反映居民消费水平的真实状况,客观识别并确定消费性支出的分布状况是构建消费支出模型的逻辑前提。
第二,将包含位置、规模以及形状参数在内的广义可加模型(GAMLSS)引入居民消费支出模型构建之中。这种设定形式既可以考虑消费支出的具体分布,又可以探究其微观影响因素。
第三,基于不同收入群体消费行为异质性的特征,本文尝试在GAMLSS框架下探讨影响不同消费群体消费水平的微观因素。
二、GAMLSS模型
如前所述,为了弥补传统的线性模型因变量多限于正态分布假定的现实困境,广义线性模型、广义可加线性模型相继被提出。但不论是广义线性模型还是广义可加线性模型,皆以因变量分布为指数型分布形态作为前提假设条件,给该模型的现实应用带来挑战。一方面是符合指数型分布族的分布类型较少,通常以正态分布、泊松分布、二项分布、Gamma分布等为主;二是现实中非指数型类分布经常出现,如一些表示效率的现象常呈现出右偏特征,如果针对这种现象进行建模,则应该选用与之相对应的右偏分布。为此,Rigby和Stasinopoulos于2005年提出了包含位置、规模和形状的广义可加模型(Generalized Additive Models for Location,Scale,and Shape,GAMLSS)。
(一)GAMLSS模型的一般形式
假设观测值yi(i=1,2,…,n)具有参数为θi=(θ1i,θ2i,θ3i,θ4i)=(μi,σi,υi,τi)的概率密度函数f(yi|θi)。其中μi、σi分别代表位置参数(通常代表均值)和规模参数(通常代表标准差),υi、τi代表形状参数,常表示偏度和峰度。GAMLSS模型的一般形式为:
令yT=(y1,y2,…,yn)为n维响应变量,令k=1,2,…,p,令gk(θi)为与分布f(yi|θi)有关的单调连接函数,设定为:

其中θk和ηk为长度为n的向量,Xk为维数已知矩阵,Zjk为维数为n×qjk的矩阵,γjk是维数为qjk的随机变量。
式(1)中,ηk(k=1,2,…,p)是由参数成分 Xkβk和可加成分Zjkγjk两部分组成。其中Xkβk为解释变量的线性函数,Zjkγjk为随机变量的线性函数(也可视为随机效应)。GAMLSS包含几种重要的模型。
当 Jk=0(k=1,2,…,p)时,模型 GAMLSS 简化为参数模型:

当Zjk=In(In为n×n的单位矩阵),γjk=hjk=hjk(Xjk),可以得到半参数可加形式的GAMLSS模型:
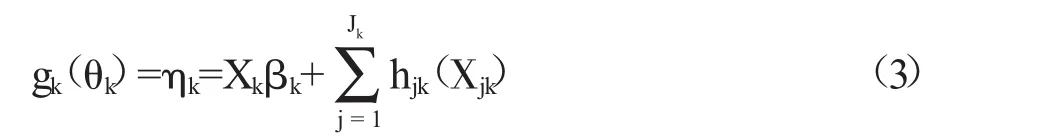
式(3)中,hjk=hjk(Xjk)为解释变量Xjk的未知函数(局部线性光滑、样条等),且hjk=hjk(Xjk)为函数hjk在Xjk处的估计值向量。
(二)GAMLSS模型的特点
GAMLSS模型的特点主要体现在三个方面:一是GAMLSS模型所用分布形式更多样,既包括传统的指数型分布,也包括大量的非指数型分布;既包括对称性分布,也包括大量具有度偏度和峰度的非对称性分布;既包括离散型分布,也包括连续性分布;既可使用单一分布,也可使用混合分布。二是GAMLSS模型允许针对位置参数(通常是平均值)、规模参数(通常是方差)以及形状参数(通常是偏度和峰度)分别独立进行建模。三是GAMLSS模型中参数模型的设定形式更多样。既可以是线性,也可以是非线性;既可以是参数形式,也可以是可加非参数形式(如参数样条、惩罚样条或局部加权回归等)。
GAMLSS这种独特的设定形式便于精准描述各个参数的影响因素的方向和程度。
(三)GAMLSS模型的估计和检验
由于GAMLSS模型不但可以对位置参数、规模参数和形状参数分别设定,也可以有多种候选分布选择,因此理论上而言,GAMLSS模型存在多种可能的设定形式。为解决模型的选择问题,基于极大似然估计(或极大似然估计的思想),Rigby和 Stasinopoulos(2005)提出使用广义赤池信息量(Generalized Akaike Information Criterion,GAIC) 和施瓦茨贝叶斯准则(SchwarzBayesian Criterion,SBC)两种统计量进行模型选择。所用公式分别为:

上式中,L为对数似然函数值,k为过拟合惩罚参数,N为模型拟合参数。通常GAIC和SBC越小,表示模型拟合越好。
三、基于GAMLSS模型的不同收入群体边际消费倾向研究
(一)统计资料来源
使用北京大学社会调查中心发布的中国家庭综合调查数据(CFPS)2010年调查资料。由于本文研究家庭消费行为及其微观影响因素,因此本文仅使用CFPS 2010中的家庭问卷以及成人问卷。
(二)不同收入群体的划分
综合看,现有文献采用相对标准界定中等收入者居多。本文采用[0.75倍收入中位数,2倍收入中位数]标准界定中等收入群体。则低于0.75倍收入中位数者为低收入群体,高于2倍收入中位数者为高收入群体。
(三)数据的描述统计分析
表1为城镇居民家庭不同收入级别人均消费性支出的描述统计结果。可以看出,在被调查的4294户城镇居民家庭中,低收入、中等收入以及高收入家庭数量分别为1638户、1782户以及874户,占比分别为38.14%、41.50%以及20.36%。三种层次的家庭消费性支出均值分别为5666.20元、9274.76元以及17065.70元,标准差分别为4468.51元、5729.54元以及11865.55元。三种层次家庭消费性支出的中位数分别为4504.50元、8102.15元和13956.67元。三种层次家庭消费性支出的偏度系数最小值为2.63,最大值为3.77,属于严重右偏特征,三种层次家庭消费性支出的峰度系数最小值为14.05,最大值为23.18,属于高度尖峰特征。取对数后,三种层次的家庭消费性支出均值分别为8.40、8.98以及9.57,标准差分别为0.66、0.57以及0.59。三种层次家庭消费性支出的中位数分别为8.41、9.00、9.54。低收入和中等收入层次家庭消费性支出偏度系数发生了质的改变,由原来的正偏,变成了负偏。而高收入群体家庭消费性支出偏度系数较之前降低了很多,达到0.06,接近对称。三种层次家庭消费性支出的峰度系数下降明显,但仍然呈现尖峰特征。
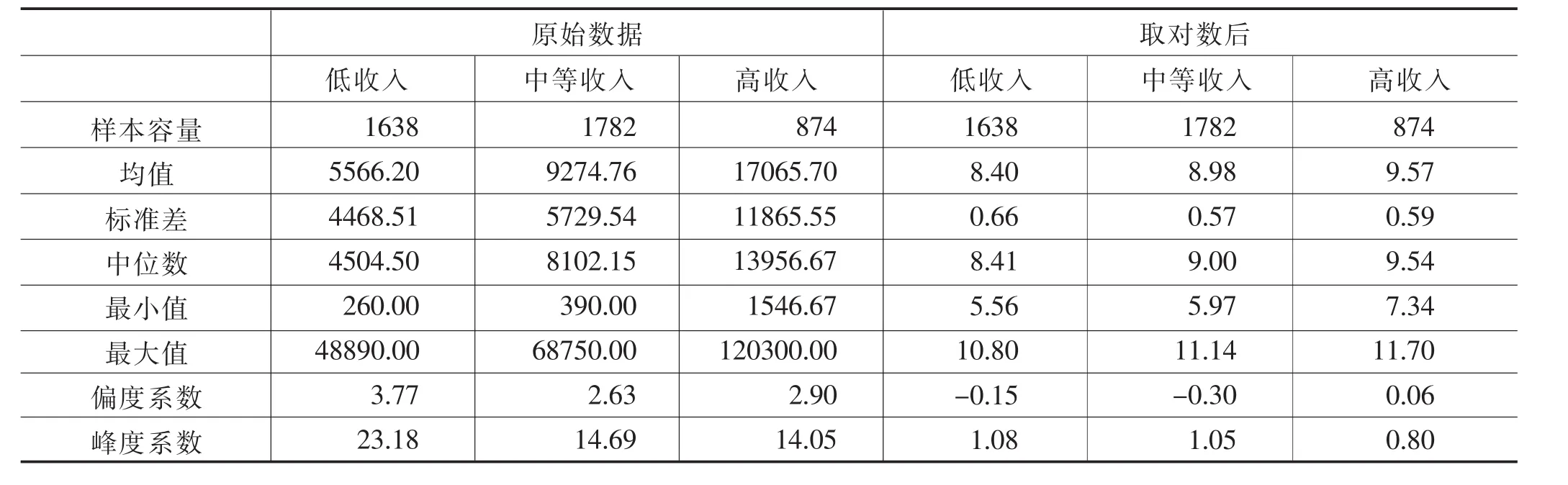
表1 城镇居民家庭人均消费性支出描述统计
(四)人均消费性支出的正态性检验
表2、表3是城镇居民家庭人均消费性支出正态性检验结果。采用了四种统计分析中常用的正态性检验方法,每种方法给出了检验统计量的数值,以及与之对应的P值。四种正态性检验的原假设都是假设研究数据服从正态分布,备择假设是研究数据不服从正态分布。表2中,所有检验的P值皆为0,说明城镇居民家庭人均消费性支出不服从正态性检验;表3中,检验的P值最大为0.0571,最小为0.0000,说明在10%的显著性水平下,城镇居民家庭人均消费性支出取对数后依然不服从正态分布。这与表1中的结果是一致的。这意味着在对居民家庭人均消费性支出数据建模时,应该考虑非正态性分布。

表2 城镇居民家庭人均消费性支出正态性检验

表3 城镇居民家庭人均消费性支出正态性检验(取对数后)
(五)居民家庭人均消费性支出统计分布的选择
由于本文对人均消费数据进行建模,且家庭人均消费额一般大于1。因此,不论是原始数据,还是经过对数性变换数据,家庭人均消费皆大于0。所以理论上来说,应该选择定义域为正数的分布函数作为候选分布。目前,gamlss软件包中定义域为正实数的分布函数共有23种①这23种分布包括指数分布(EXP)、伽玛分布(GA)、逆高斯分布(IG)、两种类型对数正态分布(LOGNO,LOGNO2)、三种类型的威布尔分布(WEI,WEI2,WEI3)、逆伽玛分布(IGAMMA)、两种帕累托分布(PARETO2,PARETO2o)、广义帕累托分布(GP)、两种 Box-Cox转换的 Cole&Green分布(BCCG,BCCGo)、指数正态分布(exGAUS)、广义伽玛分布(GG)、广义逆高斯分布(GIG)、对数正态分布(LNO)、两种类型的 Box-Cox转换的 t分布(BCTo,BCT)、两种类型的 Box-Cox转换幂指数分布(BCPEo,BCPE)、广义贝塔 II型分布(GB2)等。。
首先使用fitDist函数,对23种分布做出选择,判断哪种分布类型更适合我国居民人均消费数据。这些分布的具体分布形式可参见Mikis和Robert等(2017)[11]。所有的分布参数求解皆使用极大似然估计方法,优劣选择的判断规则是GAIC最小者为最佳分布,表4给出了按照GAIC大小排列的四种候选分布拟合结果。可以发现,适合中国居民家庭人均消费性支出的分布类型集中于广义贝塔II型分布(GB2)、两种类型的Box-Cox转换的t分布(BCTo,BCT)、两种类型的Box-Cox转换幂指数分布(BCPEo,BCPE)等三类共五种统计分布中,且这五种分布类型皆有四个参数。

表4 中国城镇居民家庭人均消费性支出分布拟合选择
在八种数据类型拟合中,有五种情形以广义贝塔II型分布(GB2)为最优,三种情形以Box-Cox转换的t分布(BCTo)为最优,综合判断,本文选择广义贝塔II型分布(GB2)度量中国居民家庭人均消费性支出。
(六)统计模型的构建
根据 Mikis和 Robert等(2017),gamlss软件包中广义贝塔 II型分布(GB2)的密度函数 GB2(μ,σ,υ,τ)为:
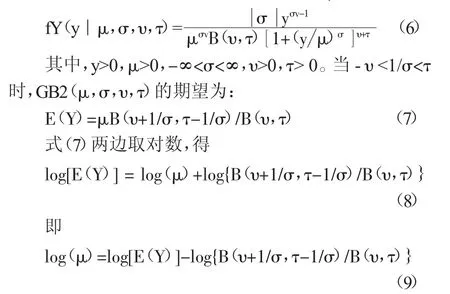
这意味着 GB2(μ,σ,υ,τ)的期望值的对数 log[E(Y)]与 log(μ)之间存在稳定的数量关系,任何关于log(μ)的函数设定形式等价于关于 log[E(Y)]的函数设定形式。
GB2(μ,σ,υ,τ)存在四个参数连接函数设定选择,而且每个参数的连接函数皆可设定为或线性、或可加、或线性与可加的综合。再加上可加项又存在三次样条、惩罚样条、分形样条、多项式等多种设定形式选择,所以理论上而言,存在多种候选设定形式。由于本文的主要目的是研究居民边际消费倾向以及影响居民消费支出水平的家庭因素,因此将研究重点集中于参数μ和σ。将参数μ的连接函数设定为对数形式,且既受到家庭人均纯收入的影响,也受到家庭变量的影响;将参数σ的连接函数设定为对数形式,且仅受到家庭人均纯收入的影响①户主年龄在一定程度上能够代表家庭所处的生命周期。;将参数υ和τ的连接函数设定为常数形式②gamlss软件包中的GB2(μ,σ,υ,τ)的默认连接函数皆为对数形式。综合比较之后,本文将参数υ和τ的连接函数设定为常数。,且不受任何解释变量的影响。综上,本文所用模型设定为:

结合公式(9),可知模型(10)中参数 α1即为边际消费倾向,本文预计不同收入层次家庭的边际消费倾向是不一样的。式(10)中∑βiXi一项的设定目的是引入除家庭人均纯收入之外的更多的解释变量。参考有关文献,本文所用解释变量的设定如表5所示。解释变量分为户主特征和家庭特征等两个方面,共有9个变量。需要说明的是,CFPS(2010)家庭问卷调查中并无户主这一项,对于2010年度调查资料,本文使用“谁是家庭主事者”来代替户主。

表5 解释变量设定
(七)模型估计结果
使用 R 软件包 gamlss,基于 GB2(μ,σ,υ,τ)分布,得到模型的估计结果,结果如表6至表7所示。从中可以发现:
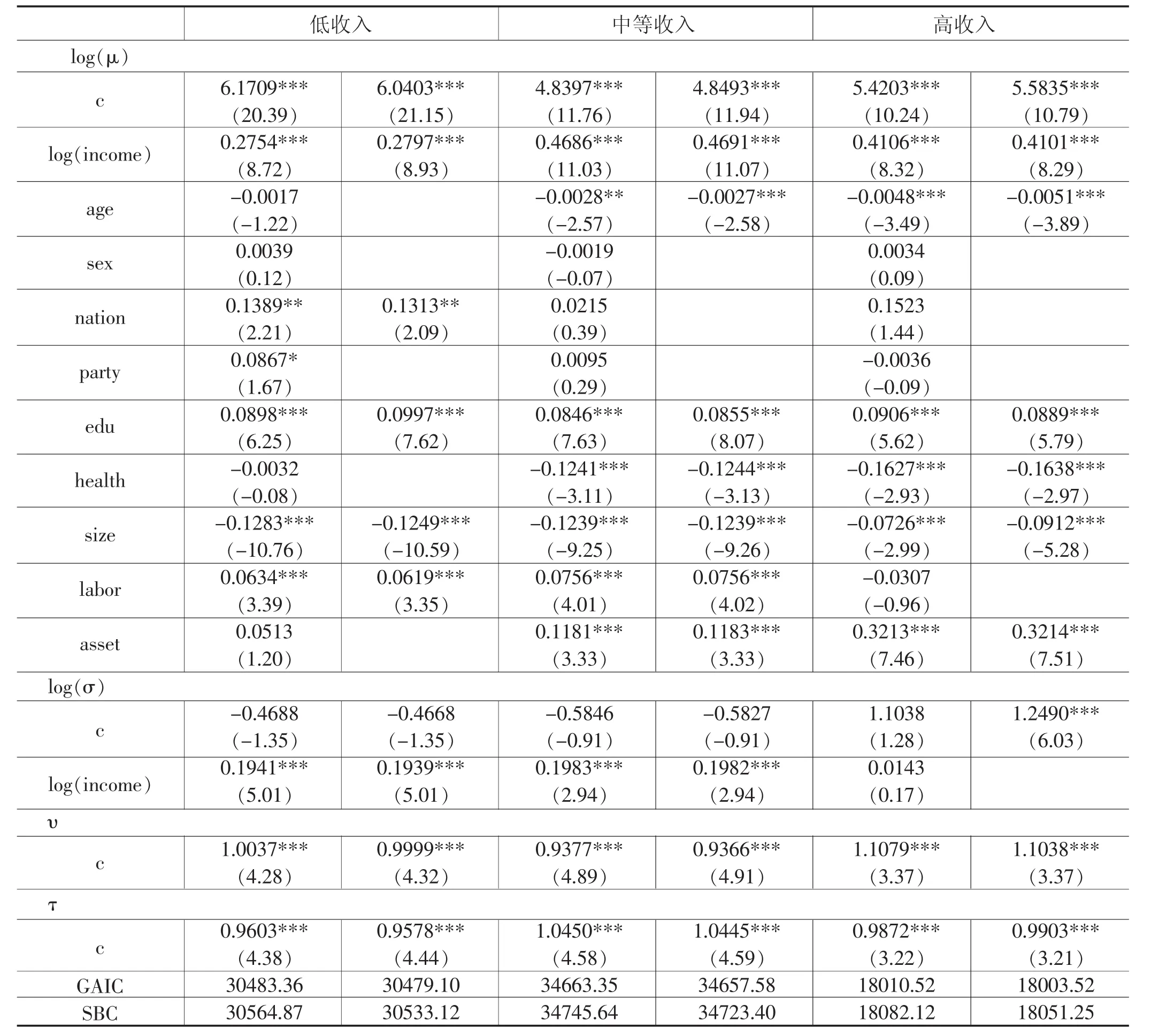
表6 中国居民家庭人均消费性支出GAMLSS回归结果分析
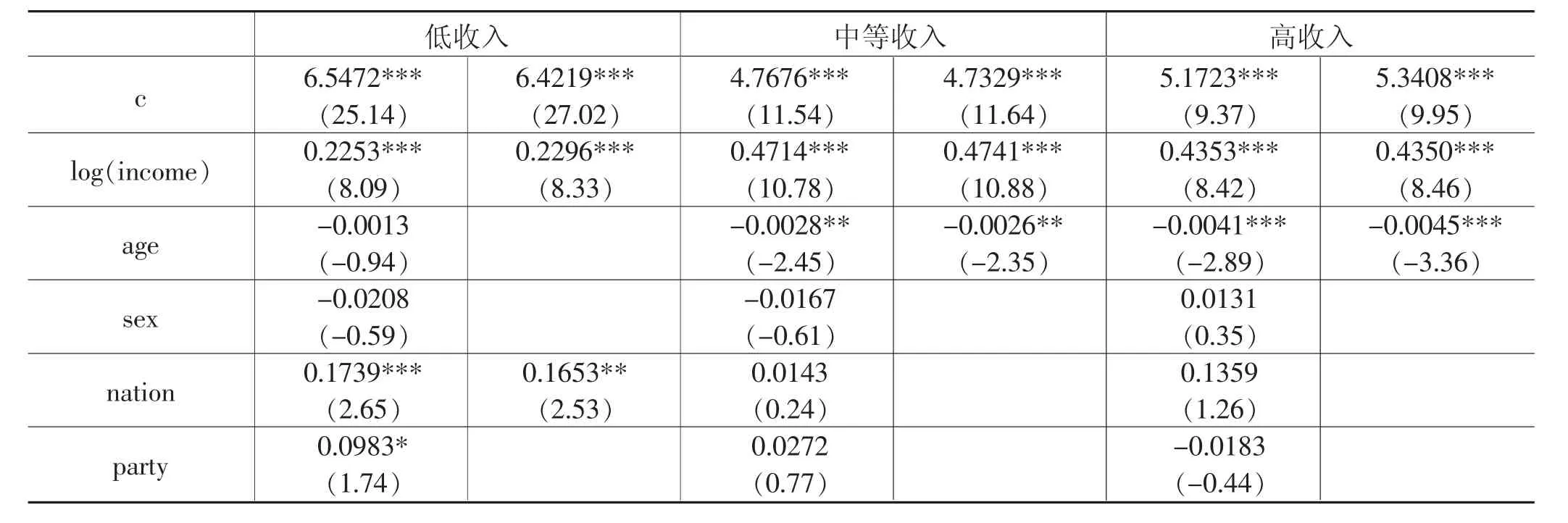
表7 中国居民家庭人均消费性支出线性回归结果分析
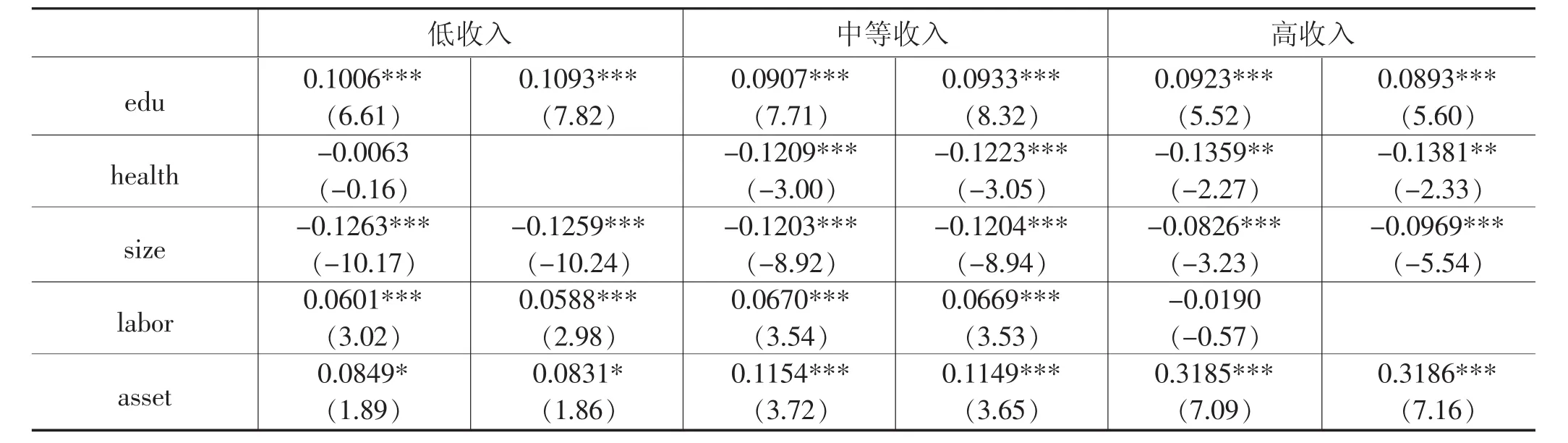
(续表)
(1)整体看,居民家庭人均纯收入对居民家庭人均消费性支出具有显著正向影响。除此以外,户主受教育程度对居民家庭人均消费性支出具有显著正向影响,而家庭人口规模对居民家庭人均消费性支出具有显著负向影响。分收入层次看,户主年龄、户主健康状况、家庭资产对中、高收入群体家庭人均消费性支出具有显著影响。而家中劳动年龄人口数仅对中、低收入家庭人均消费性支出具有显著影响。
(2)GAMLSS回归结果与线性回归结果差异性与家庭收入层次有直接关系。低收入家庭边际消费倾向系数要高于线性回归结果,而中等收入、高收入家庭边际消费倾向系数要低于线性回归结果。
(3)三种收入层次家庭的边际消费倾向由低到高顺序为:低收入群体、高收入群体、中等收入群体。该结果与杨汝岱和朱诗娥(2007)③杨汝岱和朱诗娥(2007)中假定,城乡居民边际消费倾向一致,两者的差别是通过一个城乡虚拟变量界定的,也就是假定城乡对消费的影响仅仅体现在截距项,而非斜率项。有关中等收入群体的边际消费倾向最高、低收入和高收入边际消费倾向较低的“倒U”型特征研究结果是一样的[12]。但与赵昕东和李林(2016)④赵昕东和李林(2016)中对不同收入群体的分类并没有按照收入标准,而是按照消费水平高低将家庭十等分。研究结论不一致[13]。
四、结论
构建合理有序的收入分配格局,实现各收入群体均等分享经济社会发展成果,已成为国内外学术界和政府关注的热点。边际消费倾向的研究当属该研究领域的重要方向之一。针对传统的模型构建皆以居民消费水平为正态分布为假定条件的不足,本文将包含位置、规模以及形状参数在内的广义可加模型(GAMLSS)引入居民消费支出模型构建之中,研究不同收入群体边际消费倾向问题。结果发现:
(1)居民家庭人均纯收入对家庭人均消费性支出具有显著影响,这与传统经济学理论是一致的。除此以外,户主年龄、户主受教育程度、户主健康状况、家庭资产等家庭微观变量对家庭人均消费性支出具有不同程度的影响。
(2)居民消费支出水平的分布状况会对边际消费倾向产生显著影响。不考虑居民消费支出的具体分布而直接采用正态分布,会低估低收入家庭边际消费倾向系数,高估中、高收入家庭边际消费倾向系数。
(3)整体看,不同收入群体家庭边际消费倾向分别呈“倒U”型特征。
该项研究的现实意义在于,合理有序的居民收入分配格局是激发居民消费行为的主导因素。不同收入群体共享经济发展成果的政策配套应从经济层面、社会层面等多个角度切入。

