复合材料负泊松比结构的冲击力学性能

赵昌方， 朱宏伟， 任 杰， 仲健林

(南京理工大学 机械工程学院，江苏 南京 210094)

碳纤维复合材料具有优异的吸能、比吸能、比强度、比刚度等性质[1-3]，广泛应用于汽车工业和航空航天及武器工业领域[4-7]。陈静等[8]针对汽车防撞梁开展了试验和仿真研究，并对结构参数进行了优化设计。ATAABADI等[9]通过大量实验研究了碳纤维复合材料层合结构的压溃机理，指出面内失效包括基体破碎、分层破坏、纤维断裂3种模式。庄蔚敏等[10]基于LS-DYNA有限元软件对碳纤维复合材料圆管进行了压溃模拟。负泊松比结构同样具有良好的曲面同向性、抗压痕性以及缓冲特性[11-12]。刘宇等[13]建立了钢材基的均匀蜂窝结构、角度梯度蜂窝结构、内厚度梯度蜂窝结构及高度梯度蜂窝结构，通过仿真开展了吸能、比吸能及变形模式研究。任晨辉等[14]提出了一种负刚度的负泊松比结构，并理论求解了结构的等效力学常数。于雅琳等[15]制备了一种碳纤维复合材料负泊松比二维结构，并通过数值仿真和实验获取了结构受压的泊松比变化。

目前大多数负泊松比结构的基材都是金属，体现出的情况是金属密度大，使得比吸能下降。于雅琳等[15]制备的结构属于平面二力杆，其缓冲吸能和冲击承载未曾开展研究。碳纤维复合材料与负泊松比结构的结合将会得到什么样的特性，需要进一步的研究。基于此，本研究设计了一种面内二维、空间三维的碳纤维复合材料负泊松比结构，并通过有限元仿真对不同冲击速度、不同冲击位置、不同冲击层数的冲击性能进行研究。

1 复合材料本构及失效准则

1.1 各向异性本构方程

碳纤维复合材料层合板属于典型的各向异性材料。对于单层板，其纤维横向和法向性能基本相同，通常采用横观各向同性本构模型进行描述。单层板应力和应变与刚度矩阵[Cij]的关系[16]为

(1)

(2)

式(2)中，E为弹性模量，G为剪切模量，v为泊松比。

根据坐标变化矩阵[T]和层合板理论，可得到不同角度单层板组合成的层合板的本构关系。定义材料主轴方向依次为1、2、3，正交坐标方向依次为x、y、z。取z方向(3方向)为转轴，顺着纤维方向，材料轴1与正交轴x、材料轴2与正交轴y的夹角用θ表示。坐标变化矩阵和全局本构关系如下：

T=

(3)

(4)

1.2 Chang-Chang失效准则

碳纤维复合材料的失效判据有很多，例如常见的Tasi-Wu准则[17]，Hoffman准则[18]，LaRC准则[19]，Puck准则[20]等，这些失效判据比最大应力应变失效判据更为科学合理。然而，这些复杂的失效判据在LS-DYNA中还没有被全部开发。为此，本研究选取已被开发应用的失效准则，Chang-Chang失效准则[21]。Chang-Chang失效准则考虑了基体和纤维的失效形式，包括基体拉伸和压缩失效、纤维拉伸失效，纤维失效中还考虑了纤维的横向剪切效应。失效判断方法如下：

1)基体拉伸失效。

(5)

2)基体压缩失效。

(6)

3)纤维拉伸失效。

(7)

其中，YT为基体的拉伸强度，YC为基体的压缩强度，XT为纤维在纵向的拉伸强度，S是横向的剪切强度，G是横向剪切模量。T用来判断剪切失效的状态，α是非线性剪切应力参数，计算方法如下：

(8)

(9)

当单元的应力应变关系达到这3种失效状态时，单元立刻被删除。由于没有考虑损伤演化问题，且各向异性本构模型是线弹性问题，从而使用该准则不会有渐进失效及非线性塑性的效果。但对于高速冲击问题，由于作用时间极短，通常不用考虑损伤演化及非线性问题，此时Chang-Chang失效准则具有适用性。

2 冲击吸能仿真研究

2.1 几何及材料模型

冲击吸能过程采用小球以一定的初速度撞击复合材料负泊松比结构实现，冲击几何模型见图1。小球设置为刚体，半径20 mm，材料为钢，质量为256.26 g。碳纤维复合材料的仿真参数根据文献[9]设定，材料模型为MAT-54，本构方程及失效准则见第1节。复合材料采用Shell单元进行划分，铺层厚度为1 mm、共7层，铺层规则为生产中常用的[0°/90°]。两种材料间的接触定义为面面接触，摩擦系数0.3。为了解负泊松比结构的冲击变形特性，将固定约束设置在结构左右第一个负泊松比单元的下底面。从而中部可以自由变形，吸收更多的能量，多层结构与单层结构约束方式相同。

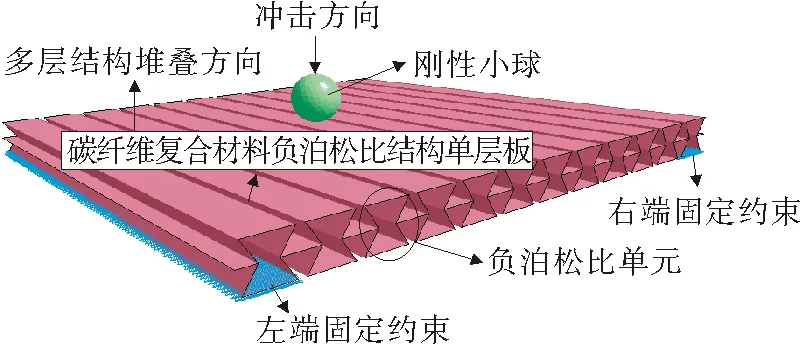
图1 单层负泊松比结构冲击吸能几何模型Fig.1 Geometric model of impact absorption for single-layer negative Poisson′s ratio structure

2.2 仿真工况设置

为了对比碳纤维复合材料负泊松比结构高低速的冲击吸能特性，本工作针对冲击速度500、200、100、10 m·s-14种工况做了仿真分析。发生冲击的位置也影响着吸能特性，本工作针对板面冲击和缝隙冲击开展了研究。负泊松比结构的层数同样对吸能效果有影响，但增加层数是否意味着吸能的增加也需要研究。因此，本工作制定的仿真工况如表1所示。缝隙冲击和板面冲击的示意见图2。

表1 仿真工况设置Table 1 Simulation conditions

图2 缝隙冲击和板面冲击情况Fig.2 Plane impact and gap impact

3 结果与分析

3.1 单层结构不同速度冲击响应

对于单层结构，开展了4种冲击速度10、100、200、500 m·s-1的仿真研究，见图3。当冲击速度为10和100 m·s-1时，小球没有穿透碳纤维复合材料负泊松比单层结构，出现回弹现象。前者没有出现任何损伤且变形较小，后者被撞了一个窟窿且弯曲变形更大。冲击速度为200 m·s-1时，碳纤维复合材料负泊松比单层结构被小球穿透，同时也发生了弯曲变形。冲击速度为500 m·s-1时，穿透后的碎屑更多，但是碳纤维复合材料负泊松比单层结构的弯曲变形较小。实际上，对于高速冲击问题，由于作用时间极短，变形仅表现在局部，属于一种高应变率状态。从这4种冲击速度的模拟结果来看，碳纤维复合材料负泊松比单层结构的冲击力学行为表现为3种，一是低速反弹，二是中速弯曲变形，三是高速穿透。

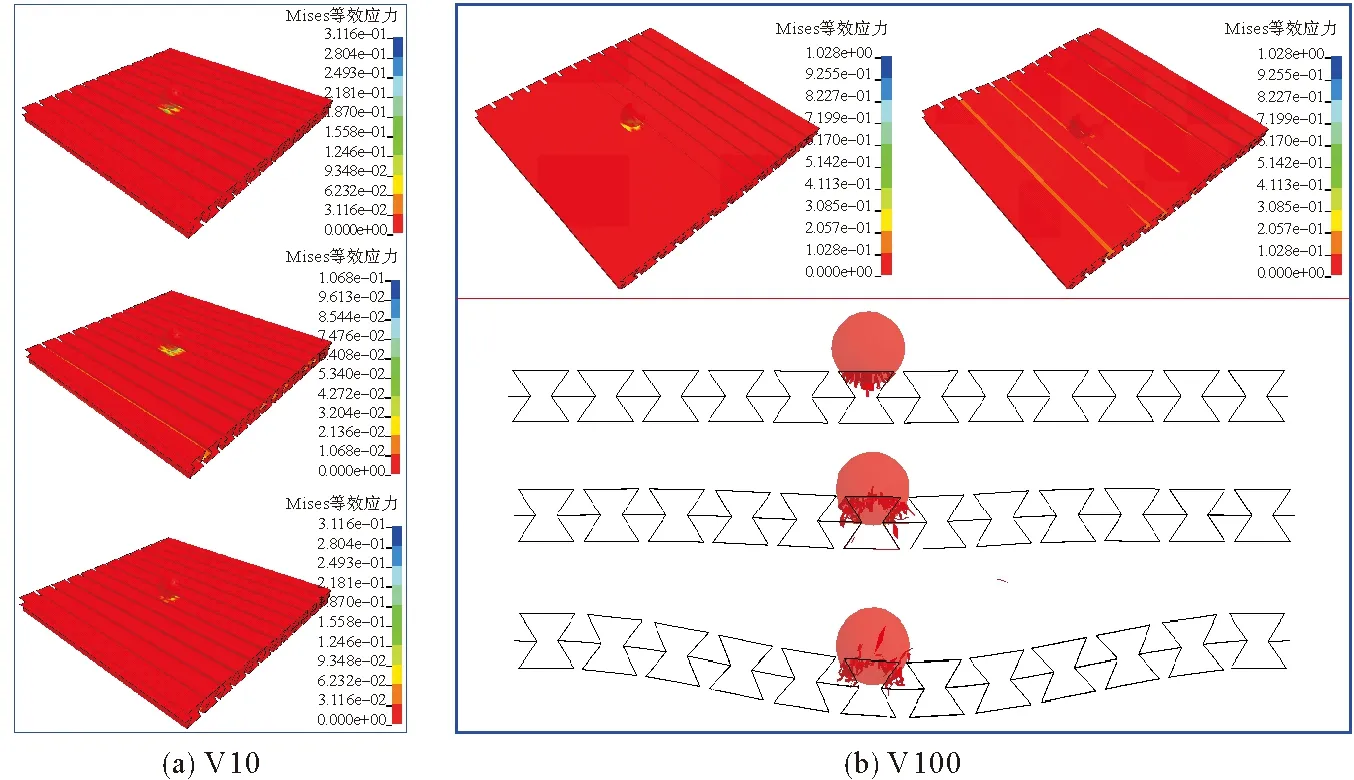
图3 不同冲击速度下单层结构的变形Fig.3 Deformation of single structures with different impact velocities

3.2 单层结构不同位置冲击响应

小球冲击碳纤维复合材料负泊松比单层结构的位置可划分为2种，一是板面冲击，二是缝隙冲击。由于冲击的位置不同，使得结构的承载性能不同，缓冲吸能效果也不同。不同速度缝隙冲击仿真结果见图4。与平板冲击的工况(图3)相比，100 m·s-1同样没有打穿，但出现了局部的破坏和弯曲变形。

图4 不同冲击位置仿真结果Fig.4 Simulation results of different impact positions

3.3 多层结构高速冲击响应

为了提升冲击吸能(本研究体现为降速效果)，增加层数是一种有效的方法。针对单层、双层、三层碳纤维复合材料负泊松比结构开展了仿真研究，结果见图5。由于是高速冲击，碳纤维复合材料体现出的压溃特性为破碎分裂，形成许多碎屑。结合图3和图5可知，这3种结构的冲击失效现象基本相同，弯曲变形很小。

图5 不同层数冲击仿真结果Fig.5 Impact simulation results of different layers

3.4 冲击性能对比分析

将上述分析工况的冲击加速度和减速速度效果绘制到图6中。对比可知，冲击速度10、100、200、500 m·s-1的减速效果依次为82.41%、85.24%、44.7%、6.8%，冲击加速度在单层板面冲击小球冲击速度为200 m·s-1时最大。综合来看，碳纤维复合材料负泊松比单层结构的中低减速效果更好。FX100的加速度峰值大于FX500大于V100和V500，这就说明缝隙冲击的受力较大，且减速效果更好。其原因在于，缝隙冲击时有两个负泊松比单元受力，横向的载荷传递更多更快，从而吸收更多的动能。随着层数的增加，加速度峰值基本相同，而减速效果逐渐增强，但并非是翻倍的增加。从比吸能(发生破坏所吸收能量的总量与其质量的比值)的角度来说，比吸能是下降的。因此，不能一味地通过增加层数来实现更高的吸能效果。

图6 不同仿真工况加速度曲线和降速效果Fig.6 Acceleration curves and deceleration effects of different simulation conditions

4 结 论

基于各向异性复合材料本构和Chang-Chang失效准则，采用有限元方法对碳纤维复合材料负泊松比结构进行了不同冲击工况的仿真研究：

1)碳纤维复合材料的中低速冲击承载和吸能效果更优；

2)缝隙冲击的减速效果和冲击承载优于板面冲击情况；

3)多层结构冲击吸能提高了，但并没有实现成倍的增加。

因此，碳纤维复合材料负泊松比结构适用于中低速缓冲吸能领域。对于高速的冲击载荷，在单个负泊松比单元重填充其他的吸能材料或者增加减速面板和拦截背板形成三明治结构是一种有效的方法。