AA6111-T4铝合金变路径成形极限研究*

杨挺 杨刚

1. 台州市黄岩区计量与产品质量安全检测研究院 浙江 台州 318020；

2. 台州科技职业学院 浙江 台州 318020

引言

板料成形过程中的失效是板料成形过程数值模拟的一大挑战。为了描述金属板料在冲压过程中的最大变形，Goodwin[1]引入了成形极限曲线（FLC）的思想，它将最大塑性变形设定在主应变和次应变的空间内。FLC自提出以来，被广泛用于确定板料成形极限。FLC通常是通过设计用于线性应变路径的实验来测量的。然而，复杂板料的成形过程和多步成形过程在冲压过程中会发生剧烈的应变路径变化。实验研究表明，应变路径的变化对板料的成形性能有很大的影响。Graf和Hosford[2]进行了AA2008-T4的实验，以研究应变路径变化对成形极限曲线（FLCs）的影响。一年后，Graf和Hosford[3]分享了他们关于应变路径变化对AA6111-T4铝合金的FLCs影响的实验结果。因此，比例应变路径下的FLC实验适用于近似线性应变路径的板料成形失效预测，但对于复杂形状板料的冲压成形或多步成形，FLC有一定的误差。

自20世纪初以来，随着先进高强度钢和铝合金的广泛应用，韧性断裂在板料成形失效预测方面引起了越来越多的关注。这是因为轻金属的失效主要是由韧性断裂引起的，几乎没有颈缩[4-5]。学者们提出了不同的韧性断裂准则来模拟不同载荷条件下板料的韧性断裂，Bai和Wierzbicki[6]修改了Mohr-Coulomb准则，用于模拟高强度钢的延性断裂。Mohr和Marcedat[7]提出了一个唯象Hosford-Coulomb模型，用于预测低应力三轴韧性断裂。Lou等[8]在压缩、剪切和拉伸的不同应力状态下，观察到沿最大剪应力方向发生韧性断裂。基于这一实验观察，Lou[9]等提出了一种基于韧性断裂微观机制的剪切韧性断裂准则，用于孔洞的形核、生长和合并。

虽然韧性断裂准则在板料成形断裂预测中的应用越来越多，但应变路径变化的影响还不清楚。本文中使用DF2012韧性断裂准则[9]，研究了应变路径变化效应。首次对AA6111-T4铝合金在比例载荷下校准DF2012准则，然后用标定准则描述了单轴张力、平面应变张力对断裂形成极限曲线（FFLC）的预应变效应。将双线性应变路径下的预测FFLCs与实验结果进行比较，分析其对FFLCs应变前影响的可预测性。

1 塑性变形模型

本文中的所有试验以及下文比例和非比例加载路径下的FFLC试验均由Graf和Hosford进行[3]。强烈建议读者参考Graf和Hosford的原始论文[3]，了解实验过程和结果的细节。

采用标准的AA6111-T4铝合金板材冲压拉伸试验，测量了比例加载下的FFLCs。通过拉伸前直径为2.54 mm的圆的变形来测量应变。单轴拉伸时的断裂应变约为0.35，平面应变拉伸时的断裂应变约为0.17，等双轴拉伸时的断裂应变约为0.244。在单轴拉伸、平面应变拉伸和双向拉伸条件下，对板材进行不同应变水平的预应变。然后从预应变板上切下试样，通过冲孔拉伸进一步拉伸，以测量预应变路径和水平的每个组合的FFLC。在双线性应变路径下测得的FFLC用于评估断裂极限的分析预测。FFLC实验的细节建议参考Graf和Hosford[3]。

为了简单起见，假设材料是法向各向异性的。在本研究中，各向异性Drucker函数[10]用于描述金属的法向各向异性。对于AA6111-T4铝合金，各向异性Drucker函数通过假设材料是平面各向同性的平均R值来校准。表1列出了校准的各向异性参数。各向异性的Drucker屈服面比Von-Mises函数更能描述平面应变拉伸下的强度。此外，由于AA6111-T4铝合金假定为平面各向同性，因此预测的R值和单轴拉伸屈服应力对加载方向不敏感。预测的R值为0.68，与实验平均R值一致。

表1 各向异性Drucker函数的参数

2 应变路径变化模型对FFLC的影响

Graf和Hosford[3]针对AA6111-T4铝合金进行了从单轴拉伸到等双轴拉伸的成形极限试验，测定了合金的断裂应变。对于双线性应变路径下的断裂应变计算，首先假设预应变路径为，对应的应力比和预应变的大小。然后，在双线性应变路径下，通过保持作为单轴拉伸、平面应变拉伸、等双轴拉伸或其他应变路径和设置作为不同的预应变值，然后，改变二次塑性变形的应变路径从单轴拉伸到等双轴拉伸。

与图1中的实验测量相比，DF2012准则能准确地预测了AA6111-T4铝合金从单轴拉伸到等双轴拉伸的FFLC。对于板料的失效模拟，预测值与实验值之间的误差是可以接受的。

图1 DF2012准则下实验与预测的FFLC比较

利用DF2012准则对单轴拉伸下的预应变效应进行理论预测，并与图2中的实验结果进行了比较。从预测和实验两方面来分析，单轴拉伸下的预应变对单轴拉伸和平面应变拉伸之间的断裂应变影响不大。另一方面，当后续应变路径从平面应变拉伸到平衡双轴拉伸时，单轴拉伸下的预应变极大地改善了成形性能。当应变路径为先单轴拉伸后平衡双轴拉伸时，断裂应变的改善达到最大值。结果表明，当应变路径按单轴拉伸和双轴拉伸顺序变化时，可以设计成形工艺和成形工具以获得更好的拉深性能。此外，值得注意的是，还有一些实验误差不容忽视。例如，单轴拉伸后单轴拉伸的断裂应变应与单轴拉伸的单应变路径的断裂应变相同，但双线性单轴拉伸的断裂应变比单轴拉伸的断裂应变高0.06左右。最后，在平面应变拉伸到平衡双轴拉伸的第二应变路径下，实验测得的FFLC值高于预测值。

图2 单轴拉伸预应变DF2012准则试验与预测FFLC比较

平面应变拉伸下预应变的预测效果与图3中的实验结果进行了比较。首先，应注意的是，即使在相同的应变路径下，单调加载和卸载再加载的实验断裂应变也有很大的差异。以平面应变为例，平面应变拉伸下的0.05预应变比单调平面应变拉伸下的断裂应变提高了约9.4%，如图3所示。平面应变拉伸下的0.11预应变比单调平面应变拉伸下的断裂应变提高了约26.2%。这在理论上不能用各向同性硬化来解释。这可归因于合金的退火或某种损伤恢复。此外，实验结果表明，平面应变拉伸下的预应变对FFLCs的形状影响不大，DF2012准则的预测结果也表明了这一点。预测还表明，在平面应变张力作用下，预应变对FLC左侧的影响可以忽略，但对右侧的FLC影响不大。

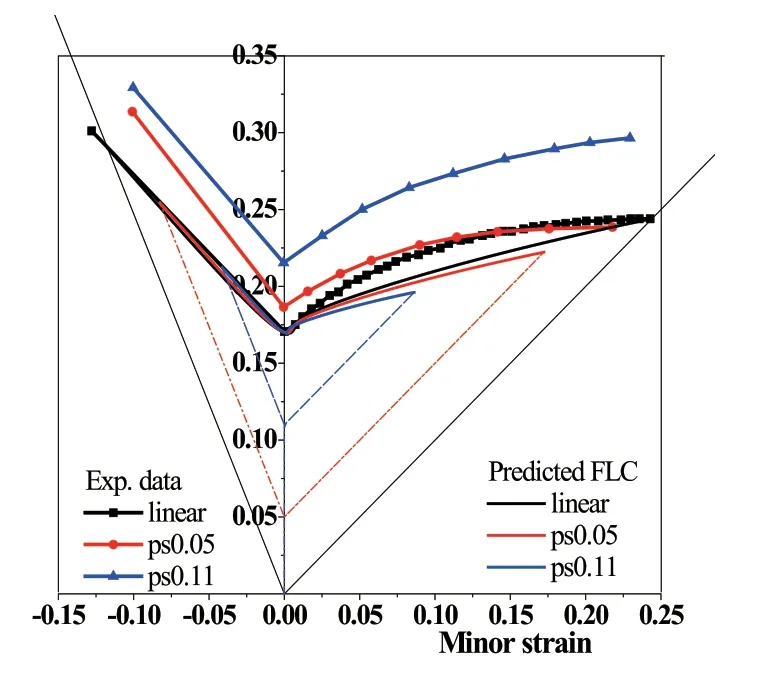
图3 平面应变拉伸下DF2012预应变准则试验与预测的FFLC比较

3 结束语

本研究旨在探讨应变路径变化对AA6111-T4铝合金断裂极限影响的DF2012准则的可预测性。将校准后的DF2012准则应用于双线性应变路径下的FFLC预测表明，DF2012准则描述了单轴拉伸、平面应变拉伸对FFLC的相似影响。但对于单轴拉伸后等双轴拉伸、平面应变拉伸后单轴拉伸等情况，预测值与实验值有较大差异。究其原因，可能是由于塑性分析模型中忽略了循环荷载效应。在这种情况下，如果将屈服面或运动硬化的演化考虑为应变路径变化的塑性，则分析预测精度将得到提高。综上所述，DF2012准则能够在比例加载下准确地模拟AA6111-T4铝合金的FFLC，并合理预测应变路径变化对FFLC的影响。