两点边值问题二尺度小波核LS-SVM解法*
张艳敏, 吴自库
(1.青岛理工大学 琴岛学院, 山东 青岛 266106;2.青岛农业大学 理学与信息科学学院, 山东 青岛 266109)
0 引 言
两点边值问题即在给定边界两点定解条件下,寻找微分方程解析解的问题。两点边值问题模型在应用科学和工程技术领域中有着广泛的应用。很多物理、航空航天、生物、化学等问题都可以用两点边值问题来描述[1-3],因此有很多学者对两点边值问题进行深入研究。然而事实表明两点边值问题很难获得解析解,因此研究其数值解法是非常必要的。传统求解方法包括刘颖[4]利用有限差分法研究了两点边值问题的数值解,该方法理论成熟,显示差分格式稳定性好,但稳定性与步长密切相关。罗炯兴[5]利用同伦分析法求解,得到了逼近解析解的函数级数形式,但随着级数项增加,逼近精度提高的同时,计算量会大幅度提升。卢仁洋等[6]采用有限元法求解了可齐次化的Dirichlet、Neumann两点边值问题,实现了对计算过程的简化。冯和英[7]采用有限体积法求解了延迟两点边值问题,提出了线性离散插值与数值积分相结合的处理方式,得到的数值解关于步长是二阶收敛的。Winfried A等[8]提出通过打靶法求解自适应两点边值问题,得到了较高的逼近精度。然而这些传统的方法为保持差分格式的稳定性,都需要对步长进行严格限制,往往计算量也比较大,因此近些年出现一些改进的软计算方法。杨云磊[9]利用神经网络法分析神经网络模型中网络拓扑结构及样本量对两点边值问题的计算结果的影响。张国山等[10-13]利用最小二乘支持向量机(Least Squares Support Vector Machines,LS-SVM)方法研究一维偏微分方程、一阶延迟微分方程、一阶微分方程的近似解中,得到的近似解具有较高的逼近精度,计算量也相对较少,还有其他改进方法[14-18]。其中,利用神经网络方法能得到稳定的解,但同时也存在多个局部极值点和隐含层数的选择问题[13],而LS-SVM 方法恰恰弥补这一不足。利用改进的二尺度小波核最小二乘支持向量机方法研究两点边值问题,不仅稳定性好、计算量小,而且精度高,近似解表达式形式简单,且连续可微,可以成为诸多领域广泛应用的方法之一。
LS-SVM 方法基本原理是首先利用基核函数整体逼近微分方程的解,然后再将问题转化为二次规划问题。利用改进的二尺度小波核最小二乘支持向量机方法,研究如下两点边值问题的近似解:
(1)
1 二尺度小波核LS-SVM的函数逼近方法

y≈f(x)=f1(x)+f2(x)
(1)
其中,


(2)

定理1 二次规划问题式(2)的解为如下方程组解。
(3)

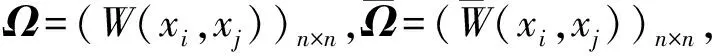
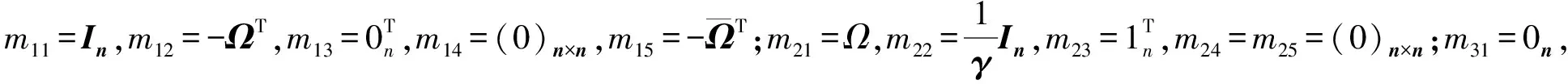
证明利用拉格朗日乘子解二次规划问题式(2),其拉格朗日函数为
由于式(1)的解在两个端点是已知的,可以对上述回归方法进行改进。令函数f(x)在区间[c,d]上连续,且f(c)=C,f(d)=D。则式(1)的近似解表示为
(4)
其中,
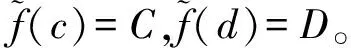
在区间内部设置训练点集{(xi,yi)|yi=f(xi),xi∈(c,d),i=1,2,…,n},带入式(4)有:
依照相同的方法可以得到回归参数。如果取B(x)≡1,A(x)≡0就是式(2)了。
为了检验二尺度小波核最小二乘支持向量机的逼近能力,这里选取文献[19]中的一个一元函数的例子,其逼近区间为[-10,10]。均选取Mexico帽小波,其小波核函数为
例1


2 二尺度小波核LS-SVM解常微分方程机制

A(x)和B(x)为已知函数,分别为
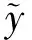
H={f∈C2[c,d]|f(c)=C,f(d)=D}
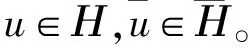
:
(
r
)=
r
″+
pr
′+
qr
首先采用第一尺度在H空间中寻求问题式(1)的近似解u,即有(u)≈g,将u代入式(1)并化简得
(5)
其中,
F(x,xj)=B(x)W″(x,xj)+(B)(x)W(x,xj)+
(p(x)B(x)+2B′(x))W′(x,xj)
记E=g-(u),则第二尺度满足方程

记
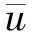

(6)
记Y(xi)=g(xi)-(A)(xi),(i=1,2,…,N),引入偏差项将训练点集代入式(5)和式(6)得:
于是参数回归问题转化为如下二次规划问题:

(7)
定理2 二次规划问题式(7)的解为如下方程的解。
(8)
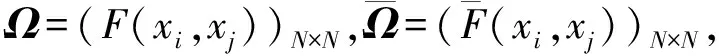
证明式(8)的拉格朗日函数为
证明方法完全类似于定理1,符号的含义也大部分相同,此处略去。
3 数值实验
选取2个数值算例检验方法的有效性。为了便于比较,两个算例均有解析解。
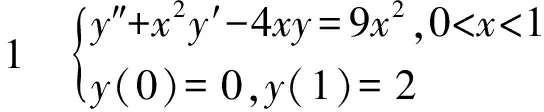
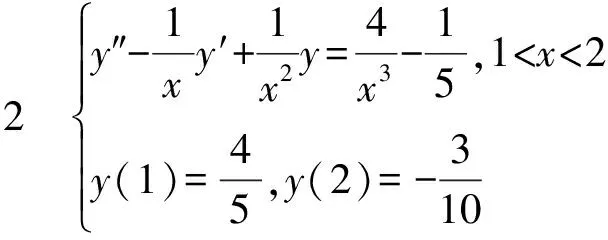

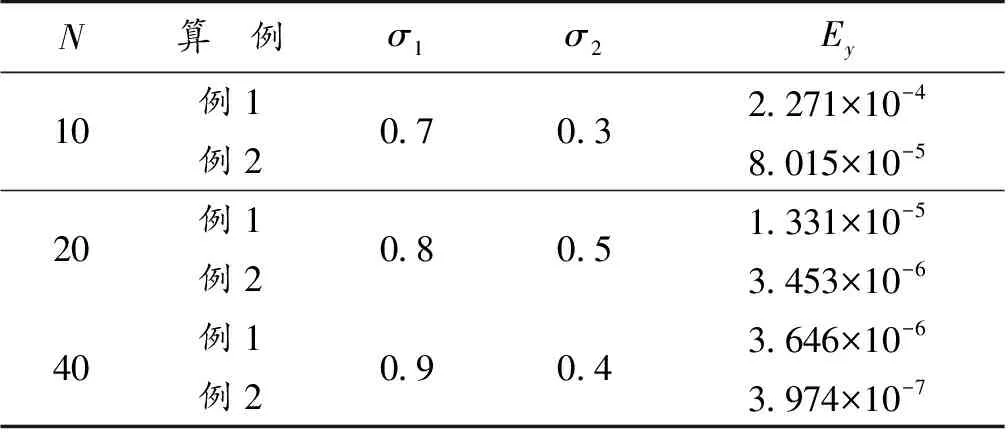
表1 数值模拟结果Table 1 Numerical simulation results

图1 N=40例1近似解曲线与误差曲线Fig. 1 Approximate solution curve and error curve of the example 1 when N=40

图2 N=40例2近似解曲线与误差曲线Fig. 2 Approximate solution curve and error curve of the example 2 when N=40
4 结束语
利用二尺度小波核LS-SVM方法研究了两点边值问题的近似解问题,推导了近似解公式。同其他已有的方法相比,方法避免了复杂微分、积分运算,同时近似解为闭式解。采用Mexico 帽小波核函数,只有两个尺度参数为可调节参数,大大减少了计算量。数值算例验证了方法求解此类问题是有效的。但是仅对线性两点边值情况进行了研究,而非线性情况的求解是更为复杂和繁琐的问题,下一步将研究利用二尺度小波核LS-SVM求解非线性两点边值问题,验证方法的有效性。
——中国制药企业十佳品牌

