一类基于梯度下降的高效分布式计算方法的应用研究

邹智康,罗元

(武汉大学数学与统计学院,湖北武汉430072)

1.引言

随着移动互联网技术的迅速发展,数据信息安全问题逐渐为人们所重视.现实生活中,数据的存储方式往往是分散的,由于数据传输成本以及机器存储的限制,互联网,金融,电子商务等行业会按区域分散设置服务器收集和存储数据.如何实现数据在不出本地机的前提下完成联合建模是当下亟待解决的技术性难题.而分布式计算是解决此问题的有效途径之一,并且由于其高可靠,可容错和易扩展的天然优势,结合大数据时代背景,在高维回归问题中极具应用前景.

至今为止,衍生出了许多分布式计算方法.比如说,文[1-2]通过平均不同本地计算机上的结果来估计实际参数.Jordan等[3]开发了一种通信有效的替代似然函数方法,即CLS(Communication-efficient Surrogate Likelihood).CLS可用于低维模型参数估计,高维正则估计和贝叶斯推断.WANG等[4]通过在不同的本地机上使用梯度信息解决ℓ1正则化M估计问题并提高了计算效率.

另一方面,高维稀疏条件下的特征筛选和参数估计一直是统计相关学科关注的热点之一.其中,惩罚方法扮演着重要的角色.Tibshirani[5]提出了ℓ1正则化方法,即Lasso(The Least Absolute Shrinkage and Selectionator operator)方法.然而Lasso方法通常会过度压缩较大的系数,从而导致估计有偏差,因此统计学家考虑使用非凸惩罚,比如,FAN和LI[6]提出的SCAD(The Smoothly Clipped Absolute Deviation)方法以及ZHANG[7]提出的MCP(The Minimax Concave Penalty)方法都是解决此类问题的代表性成果.但是,在解超高维问题,尤其当维度p是样本n的指数级时,即p=O(exp(n)),正则化方法存在不稳定不收敛等问题.为此,HUANG[8]提出了交替选择支撑集并在支撑集上估计参数的SDAR方法来解决ℓ0惩罚问题.SDAR方法是基于ℓ0正则化最小二乘问题的KKT条件所提出来的,具有收敛快,精度高的优点,且可以估计出真实的支撑集并得到参数的Oracle估计.本文在SDAR算法的基础上,提出了一种分布式的SDAR方法,简记为GDSDAR.在GDSDAR算法中,我们利用梯度下降法来解决SDAR算法中一系列的最小二乘问题,其中梯度信息的传递保证了在联合建模过程中原始数据的私密性,同时满足高维稀疏计算以及数据安全的要求.

2.问题简介

3.实验结果与分析

由表3.1结果分析可知,其他参数保持不变,随着样本总量N的增加,三种算法的相对误差(RE)值的变化没有统一趋势,但在每种情形下,GDSDAR算法的精准度都是最优的.对于正确指标覆盖率ICR,LASSO与其他两种方法相比,覆盖率最小,SCAD方法在样本量偏低时表现最好,而当样本总量N增加到一定程度后,GDSDAR方法的ICR指标最优.此外,从计算时间的角度分析,三种算法运行所需的平均时长会随着样本总量N的增加而延长.但是在每一种情况下,GDSDAR算法的平均时长最短且波动幅度与另外两种算法相近.综上所述,GDSDAR算法在每种情形下都有着最好的精准度和最高的计算效率,且当样本总量偏大时,正确指标覆盖率表现更优.

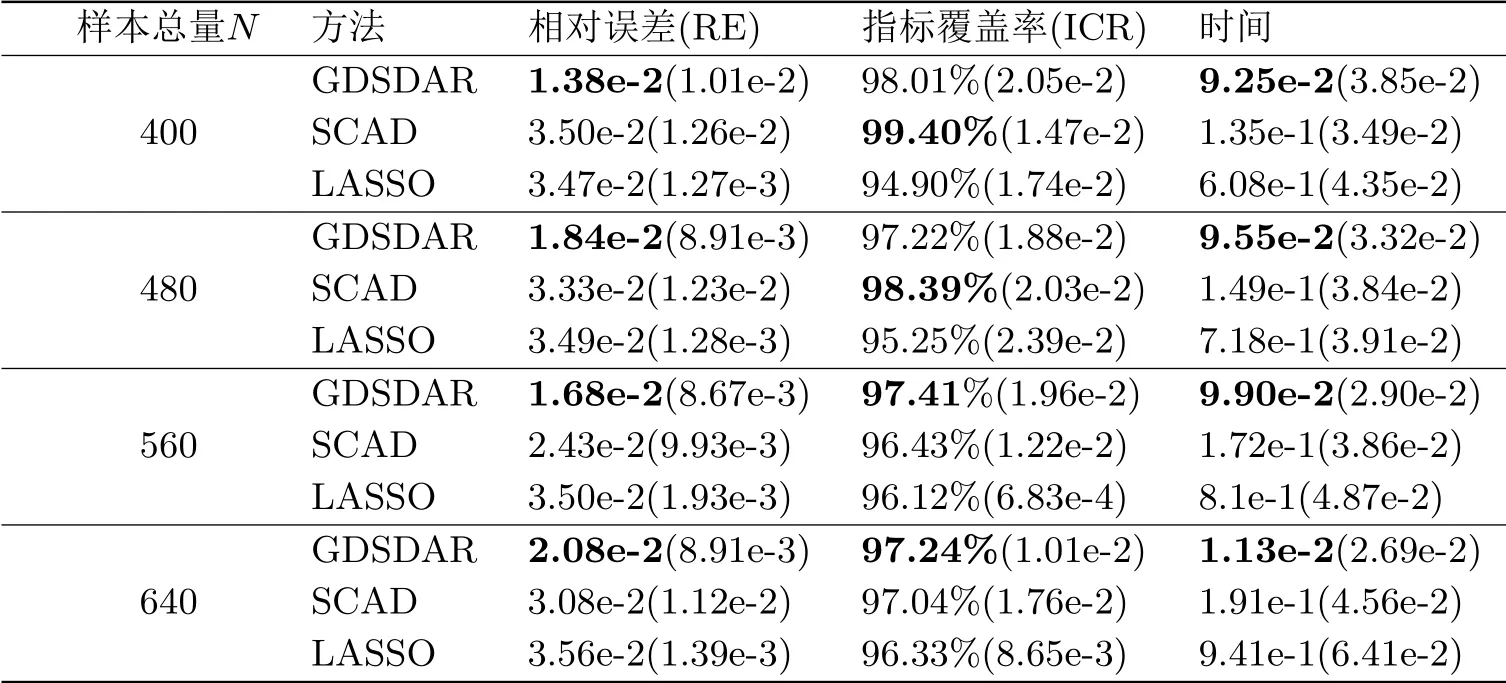
表3.1 不同样本总量N下三种算法的比较

根据表3.2中的数据分析可知,在其他参数保持不变情况下,随着稀疏度s的不断增大,三种方法中只有GDSDAR结果的RE值在不断下降,始终保持着最高的精准度,而另外两种方法的RE值则不断增加,与GDSDAR的精度差距逐渐拉大,说明我们的方法对中等稀疏问题仍然有效.至于正确指标覆盖率,GDSDAR和SCAD方法随着s值的增加,ICR指标都稳步提升,一度达到99%的准确率,LASSO方法的ICR指标在大幅降低,从一开始的96.72%陡降至62.67%,说明LASSO方法不适用于中等稀疏问题.综上所述,在保证较高指标覆盖率的前提下,GDSDAR拥有更高的精准度,且在稀疏度K较大时,表现更好.

表3.2 不同稀疏度s下三种算法结果比较

分析表3.3数据可知,其他参数保持不变,当数据相关性ρ变高时,GDSDAR、LASSO结果的相对误差都在不断降低,而SCAD结果的相对误差则在不断增大,从总体上看,GDSDAR算法的RE值最小,精准度最高.对于正确指标覆盖率,GDSDAR、SCAD两种方法在相关性变高时,ICR指标逐渐增大,而LASSO方法表现呈下滑趋势.相比而言,GDSDAR在低相关性条件下更有优势,SCAD在高相关性条件下会略胜一筹.综上所述,GDSDAR算法在相关性变动的情况下,精准度都有良好的保证,且正确指标覆盖率较高.

表3.3 不同相关程度ρ下三种算法结果比较

4.结语

本文提出了一种求解分布式情形下高维稀疏参数估计的算法GDSDAR.创新点主要体现在两个方面.一方面,GDSDAR方法可以解决分散存储数据的联合建模问题,在运算过程中,发生信息交互的仅仅是梯度向量而非数据本身,所以能够保证本地数据的私密性,考虑到当今社会对于信息安全的重视程度,这一特性使得GDSDAR算法拥有广泛的应用前景.另一方面,在高维稀疏的假定下,GDSDAR算法通过对ℓ0约束最小化KKT条件的改进,交替选择支撑集的方式并在支撑集上估计参数.实验表明,相较于经典的ℓ1正则化方法,GDSDAR无论在精准度或是指标正确覆盖率两方面都有着优异的表现,稳定性也十分出色.

除了上述的创新点,GDSDAR算法仍然存在一些后续的问题.例如在每次运行算法前,我们需要依据经验事先确定模型大小,然后据此得到相应的模型.在接下来的研究中,我们考虑运用交叉验证或者统计学中的HBIC指标辅助判断合适的模型大小,这种改进将会使GDSDAR算法更适用于真实数据的建模计算.