Global Boundedness and Asymptotic Behavior in a Chemotaxis Model with Indirect Signal Absorption and Generalized Logistic Source
WANG Weifeng(王维峰),MA Heping(马和平)
( 1.School of Mathematics and Statistics,South-Central University for Nationalities,Wuhan 430074,China;2.School of Science,Hubei University of Technology,Wuhan 430068,China)
Abstract:In this paper,we consider the chemotaxis model with indirect signal absorption and logistic-type source in a bounded domain with smooth boundary.Under appropriate regularity assumptions on the initial data,we show that the system possesses a unique and global bounded classical solution.In addition,the asymptotic behavior of the solutions is discussed.Our results generalize and improve partial previously known ones,and partially results are new.
Key words:Chemotaxis;Asymptotic behavior;Indirect signal absorption;Logistic-type source
1.Introduction
Chemotaxis,the directed movement of cells or organisms in response to the gradients of concentration of the chemical stimuli,plays essential roles in various biological processes such as embryonic development,wound healing,and disease progression.A classical mathematical model for chemotaxis was introduced by Keller and Segel in[8]to describe aggregation of cellular slime mold toward a higher concentration of a chemical signal,which reads
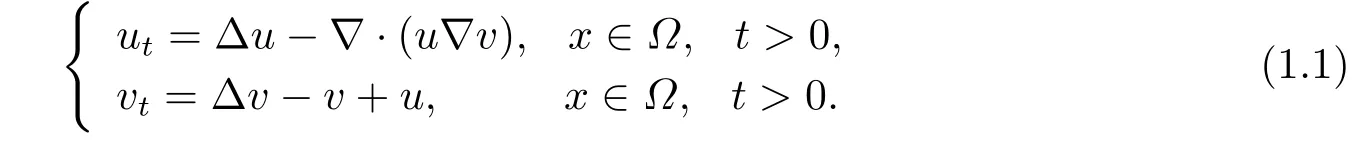
The mathematical analysis of(1.1)and the variants thereof mainly concentrate on the boundedness and blow-up of the solutions[5,20,24].As the blow-up has not been observed in the real biological process,many mechanisms,such as nonlinear porous medium diffusion,saturation effect,logistic source,may avoid the blow-up of solutions[13,15,18].In the past few decades,the system(1.1)has attracted extensive attentions.For a helpful overview of many models arising out of this fundamental description we refer to the surveys in[2-4].
However,some organisms may be toward the higher concentration of nutrient(e.g.oxygen)which is consumed rather than produced:





2.Proof of Theorem 1.1






3.Proof of Theorem 1.2




- 应用数学的其它文章
- 一类基于梯度下降的高效分布式计算方法的应用研究
- 通胀风险和最低保障约束下基于二次效用函数的DC型养老金最优投资策略
- 三维不可压磁微极流的投影统计解及其退化正则性
- Dynamic Feedback Stabilization for Timoshenko Beam with Locally Input Controls and Input Distributed Delay
- 一类奇异抛物方程淬火解的数值分析
- Convergence Rate Analysis of a Class of Derivative-Free Projection Methods for Convex Constrained Monotone Nonlinear Equations

