晶粒尺寸对多晶铜接触力学特性的影响

林起崟 张瑜寒 洪 军 王 晨 张宁静

1.西安交通大学现代设计及转子轴承系统教育部重点实验室，西安，7100492.西安交通大学设计科学与基础部件研究所，西安，710049

0 引言

机械装备中存在大量的结合面(又称装配连接界面)，结合面的存在破坏了机械结构力和转矩传递的连续性，因此它对整机性能具有举足轻重的影响[1]。结合面从微观上看是由众多高度不同的微凸体构成的，并且结合面的表面形貌具有多尺度特征，其表征尺度可达纳米尺度[2]。接触刚度作为描述结合面接触力学性能的重要参数之一，其大小会直接影响整机的静动态特性[3-4]。此外，材料的表面硬度作为结合面的重要材料力学性能参数，与接触刚度有十分密切的关系[5]。由于宏观连续介质理论已不再适用于纳米尺度接触问题的研究，而实验法也难以观察到材料纳米尺度下内部的原子运动情况，且材料加工费用昂贵、耗时长，因此分子动力学(molecular dynamics，MD)模拟方法[6-7]凭借其成熟的理论和高效的计算等优点成为了微纳尺度下接触研究中应用最为广泛的数值方法[8]。

针对结合面的接触研究，已有许多学者建立了很多分子动力学数值接触模型。在单微凸体接触模拟方面：黄健萌等[9]开展了两种不同形状的金刚石压头与单晶铜基体的黏着接触分子动力学仿真，发现由于半球形压头底部表面积比圆锥形压头底部表面积更大，导致半球形压头与基体之间的引力更大，从而更易产生黏着接触现象并且下压过程中半球形压头所受到的法向接触力更大；YANG等[10]在微观尺度下用原子模拟的方法对连续介质接触理论进行了验证，模拟了名义光滑的球形压头与空间平面基体的接触与分离过程，发现最大法向接触力的大小与压头的尺寸相关，并且在压入的过程中伴随有不同位错的成核、运动、湮灭；MOJUMDER等[11]开展了纯铝的纳米压痕分子动力学模拟，发现随着压头尺寸的增大，压头与基体的接触面积变大，压痕力和位错密度相应更大，并且硬度和弹性模量均增大；樊江等[12]建立了球状微凸体剪切运动过程的分子动力学模型，分析了单晶铜微凸体在剪切运动过程中切向接触力和法向接触力随微凸体半径的变化规律，发现单晶铜在真空中发生干摩擦时滑动摩擦因数只与微凸体形状参数有关。

在多微凸体粗糙表面的接触模拟方面：SANTHAPURAM等[13]建立了包含有球形微凸体和圆柱形微凸体的粗糙铝表面分子动力学接触模型，对比了这两种粗糙表面的接触力学响应。黄仕平等[14]采用分子动力学-格林函数法模拟了高斯粗糙表面的接触过程，探讨了由微球体组成的粗糙面的接触力学特性，模拟发现，在微凸体高度符合高斯分布的情况下，接触面积与接触力成线性关系。YASTREBOV等[15]采用分子动力学方法模拟了分形粗糙表面与弹性半空间体的无摩擦以及无黏着接触过程，研究了Nayak参数对接触面积演化的作用，结果表明，在给定的归一化压力下，接触面积随Nayak参数变化呈现对数递减趋势。

上述研究均主要着眼于粗糙表面的微观几何形貌结构对其接触功能属性的影响机理，并未针对接触表面的材料力学性能参数(如表面硬度)对接触性能的影响展开研究。本文基于混合势函数(EAM和Morse)，采用Verlet算法对刚性半球形金刚石压头与弹塑性多晶铜基体的分子动力学黏着接触与分离过程进行了仿真，从能量角度分析了不同晶粒尺寸对多晶铜基体的纳米硬度和接触刚度的影响规律。通过揭示多晶铜基体亚表面的变形机理，从原子尺度解释了上述规律现象产生的原因。

1 分子动力学建模与计算方法

1.1 建模与仿真

刚性球体与弹塑性半空间体的接触模型是接触力学方面研究所采用的经典接触模型之一[16]。图1为本文构建的分子动力学接触模拟仿真模型的XY平面示意图。该模型由上下两部分构成，上半部分为金刚石压头，鉴于典型Berkovich压头的尖端在纳观尺度下为半球形，因此本模拟中压头的形状选取为半球形，综合考虑压入深度与基体尺寸，选取压头的半径为3.5 nm；下半部分为多晶铜基体，其三个维度的尺寸分别为50a×50a×30a，a为晶体铜的晶格常数。由于金刚石的硬度远远大于铜材料的硬度，因此在接触模拟过程中将金刚石压头视作刚体，即不需要用势函数来描述C原子之间的相互作用力。多晶铜基体采用Voronoi-tesselation方法[17]生成，由许多相同晶粒尺寸的单晶铜晶粒组成，其平均晶粒尺寸G分别为12 nm、10 nm、9 nm、8 nm、7 nm和6 nm，组成多晶铜的各单晶铜晶粒取向为随机取向。在模拟过程中多晶铜基体会发生弹塑性变形。将多晶体基体自上而下依次分为三个部分，依次为牛顿层、恒温层和固定层，其中基体的弹塑性变形将发生在牛顿层。图1中，hmax为压头在模拟过程中将要下压的最大压深，压入方向竖直向下。金刚石压头与多晶铜基体在正式模拟前的初始间距为1 nm，此距离保证了在模拟开始前压头中的C原子与基体表层的Cu原子之间无相互作用力。

图1 金刚石压头与多晶铜基体的分子动力学接触模型XY平面示意图Fig.1 Molecular dynamics contact model of diamond indenter and polycrystalline copper matrix schematic diagram of XY plane

势函数影响着模拟的精度，决定着模拟结果的可靠性。由于物质的原子和分子构造不同，造成原子间的相互作用类型不同，因此必须采用不同类型的原子间相互作用势。金刚石立方晶体结构的晶格常数a为0.357 nm，模拟过程中忽略C—C原子之间的相互作用。多晶铜的组成晶粒为面心立方(face center cubic，FCC)晶体结构，其晶格常数a为0.3615 nm，对Cu—Cu原子之间的相互作用力采用EAM势函数[18]进行描述。EAM势是一种多体势，能够较好地描述金属晶体的结构特性和力学特性，在金属体系的分子动力学模拟中应用广泛。C—Cu原子之间的相互作用力采用Morse势函数[19]进行描述。Morse势是一种对偶势，适用于表征不同原子间的相互作用力，广泛应用于金刚石与金属原子间相互作用力的描述。Morse势函数表达式中包含3个可调参数，参数值的设置参考了已有相关研究报道[20-24]，分别为D=0.087 eV，α=51.4 nm-1，r0=0.205 nm，其中D为结合能系数，α为势能曲线梯度系数，r0为原子间作用力为0时的平衡态原子间距。多晶铜基体的X、Y、Z轴的晶向分别取[100]、[001]和[010]。在模拟系统的X、Z方向上均选取周期性边界条件以消除尺寸效应，在Y方向上选取自由边界条件。在模拟过程中，固定层原子的位移与受力在每个时间步上均不更新；对属于恒温层原子的信息采用Nose-Hoover热浴耦合算法[25]进行控制，可使得恒温层的温度在模拟期间保持为设定值；对牛顿层的原子采用Verlet算法[26]进行牛顿运动方程的求解并更新每时刻原子的位置与速度。模拟的时间步长取值为1 fs。

本文模拟在常温下的接触行为，正式模拟开始之前，先使系统经历弛豫过程，采用Berendsen热浴耦合算法[27]将体系加热至模拟温度300 K，弛豫过程中系统状态参数的变化趋势表明，30 ps的总弛豫时间可使得体系的温度和总能量达到充分稳定的状态。模拟开始时，对金刚石压头施加位移载荷，研究结果表明，加载的速度对仿真的结果影响不大[28]，因此使压头沿着Y轴负方向以100 m/s的速度做匀速运动，并逐渐压入多晶铜基体，最大压深为2 nm，基体在此下压速度及压深下可达到一定的塑性变形量。在达到最大压深后，对金刚石压头施加反向且相同大小的位移载荷，使其逐渐与基体脱离接触并匀速回到初始位置。模拟过程中记录多晶铜基体对金刚石压头施加的法向载荷F。本文的模拟过程采用开源分子动力学软件LAMMPS完成。

1.2 压痕功法

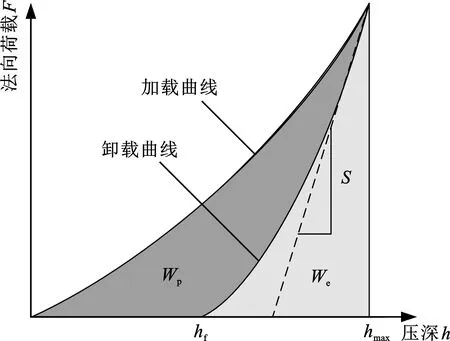
图2 典型加载-卸载曲线Fig.2 Typical loading-unloading curve

如图2所示，压痕功法[29]认为表面压痕的形成过程是能量消耗或做功的过程。

在接触过程中，加载曲线对X轴进行积分得到的面积是压头做的总功Wt，在分离过程中，卸载曲线对X轴进行积分得到的面积是弹性功We，二者之间的差值就是塑性功Wp，可表示为

Wp=Wt-We

(1)

其中，总功Wt和弹性功We可分别表示为

(2)

(3)

式中，h为压头下压的位移；Fload(h)表示加载曲线；Funload(h)表示卸载曲线。

纳米硬度Hp定义为

(4)

式中，Fmax为接触过程中压头受到的最大法向接触力；k为与压头形状有关的常数，在本模拟中取k=0.0408。

1.3 弹性接触刚度

由图2可以看出，随着压入深度的不断增大，压头受到的法向接触力也随之不断增大，当压入深度到达设定值后压头停止下压。在完全脱离接触后，基体压深会回到一个固定值，将此时的深度称为残余深度hf，即压头在材料表面上留下的永久塑性变形。在卸载曲线顶端的起始点处作一条切线，将该切线的斜率称为接触刚度S。

采用如下幂函数来拟合卸载曲线顶端部分：

Funload(h)=β(h-hf)m

(5)

其中，β、m为卸载曲线的拟合参数。则接触刚度S的计算公式为

S=βm(hmax-hf)m-1

(6)

1.4 Hertz接触理论计算

在不考虑表面黏着力存在的情况下，Hertz接触理论给出了压头与基体弹性接触时法向载荷F、压头半径R、压入深度h之间的函数关系式：

(7)

(8)

式中，E*为复合弹性模量；Es、Ei分别为基体和压头的弹性模量；υs、υi分别为基体和压头的泊松比。

本模拟中，半球形金刚石压头与多晶铜基体的弹性模量和泊松比参数分别取值为：Ei=1141 GPa，Es=115 GPa；υi=0.07，υs=0.25。

2 结果与讨论

2.1 法向接触力的变化

图3为不同晶粒尺寸G下法向接触力随压头下压位移的变化曲线，其中黑色和蓝色曲线分别为由分子动力学(MD)模拟得到的金刚石压头所受到的多晶铜基体在接触和分离过程中施加的法向接触力，红色曲线为接触过程中由Hertz理论拟合得到的法向接触力。由图3可以看出，载荷-位移曲线呈现波动的状态，载荷的波动与基体铜的晶格变形、晶格重构还有材料的非晶相变有密切的关系。

图3a～图3f中的A点代表压头即将开始压入多晶铜基体的临界点。可以看出在不同晶粒尺寸条件下，压头未压入基体前均出现了数值很小的负方向的力，这表明此时金刚石压头与多晶铜基体原子之间的吸引力起主要作用。文献[30]指出：基体会因为引力过大而引起基体表面部分原子发生纳米尺度接触所特有的“突跳”现象。当两表面静止接触或两表面间隙处于纳米量级时，由于黏着力的作用，使得两表面黏附而不易分离。如图4所示，不同晶粒尺寸条件下金刚石压头所受到的最大黏着力基本不变。这是因为黏着力的大小主要与表面能有关，相同的压头尺寸使得压头所接触的表面积相同，所以最大黏着力的变化基本不大。

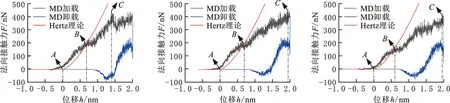
(a)G=12 nm (b)G=10 nm (c)G=9 nm

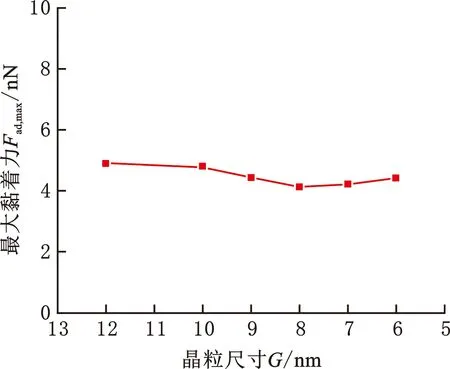
图4 最大黏着力随晶粒尺寸的变化曲线Fig.4 Variation curve of maximum adhesion force with grain size

随着压头逐渐压入基体，金刚石压头受到的多晶铜基体施加的法向接触力逐渐增大。值得注意的是，无论何种多晶铜晶粒尺寸的条件下，在图3a～图3f中B点之前，由MD模拟得到的法向接触力要比Hertz理论拟合得到的法向接触力大。这是因为在压深很小时，基体处于弹性变形阶段，Hertz理论的适用对象是表面光滑的弹性变形体，接触过程连续且无摩擦，不存在相对滑动，可忽略黏着力和表面力的存在，而MD模拟在原子尺度下包含了上述因素。当压深逐渐增大且超过B点处压深后，基体逐渐开始由弹性变形过渡到塑性变形，Hertz理论忽略了塑性变形的影响，仅适用于弹性形变，从而使得MD模拟的法向接触力比Hertz理论拟合的法向接触力小。

(9)

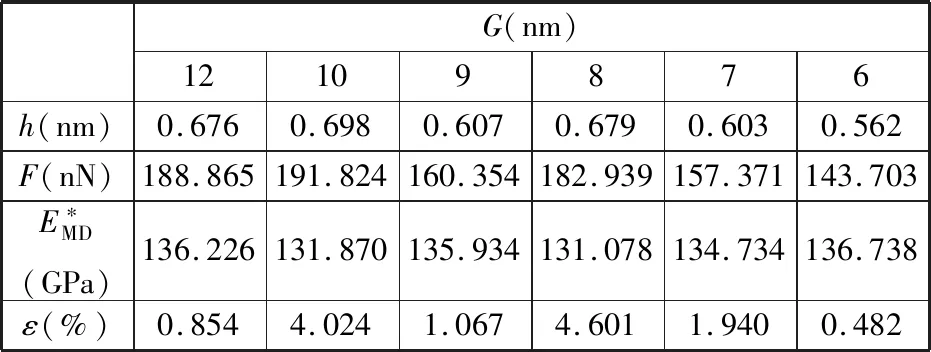
表1 不同晶粒尺寸条件下由MD模拟计算得到的复合弹性模量Tab.1 The composite elastic modulus calculated by MD simulation under different grain size conditions

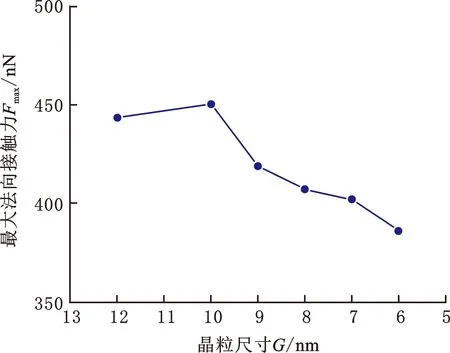
图5 最大法向接触力随晶粒尺寸的变化曲线Fig.5 Variation curve of maximum normal contact force with grain size

图3a～图3f中的C点处的法向接触力为MD模拟得到的不同晶粒尺寸条件下半球形金刚石压头受到的多晶铜基体施加的最大法向接触力。根据图5中的曲线可以看出，当晶粒尺寸大于10 nm时，随晶粒尺寸的减小，压头受到基体施加的最大法向接触力呈现增大的趋势，表现出细晶强化效应(即霍尔-佩奇现象)；而当晶粒尺寸小于10 nm时，最大法向接触力随晶粒尺寸的减小呈现减小的趋势，显示出明显的反霍尔-佩奇现象。这是因为霍尔-佩奇公式是根据位错塞积的强化作用而提出的，当晶粒尺寸为纳米级时(小于10 nm)，晶粒中可存在的位错极少，故霍尔-佩奇公式就不再适用。

当压头压入基体达到最大压深时，对压头施加反向且相同大小的位移载荷，压头与基体随即进入分离阶段。由图3a～图3f可以看出，不同晶粒尺寸条件下，压头与基体开始分离时法向接触力迅速减小，当压深回复到1.5 nm左右时，压头受到的法向接触力均出现负值的情况，这是由于卸载过程中多晶铜基体的原子与金刚石压头原子之间的吸附作用导致的。随着压头的上升吸附效应逐渐增强，最终压头原子会离开基体原子的作用范围，即压头不再受力。

2.2 接触过程的能量分析

图6所示为根据压痕功法计算得到的不同晶粒尺寸条件下压头与基体接触以及分离过程中体系能量的变化情况。可以明显看出，在模拟过程中，体系的总能量Wt、弹性能We以及塑性能Wp均与图5所示的压头受到基体施加的最大法向接触力的变化趋势一致，即表现出先增大而后又减小的变化趋势。

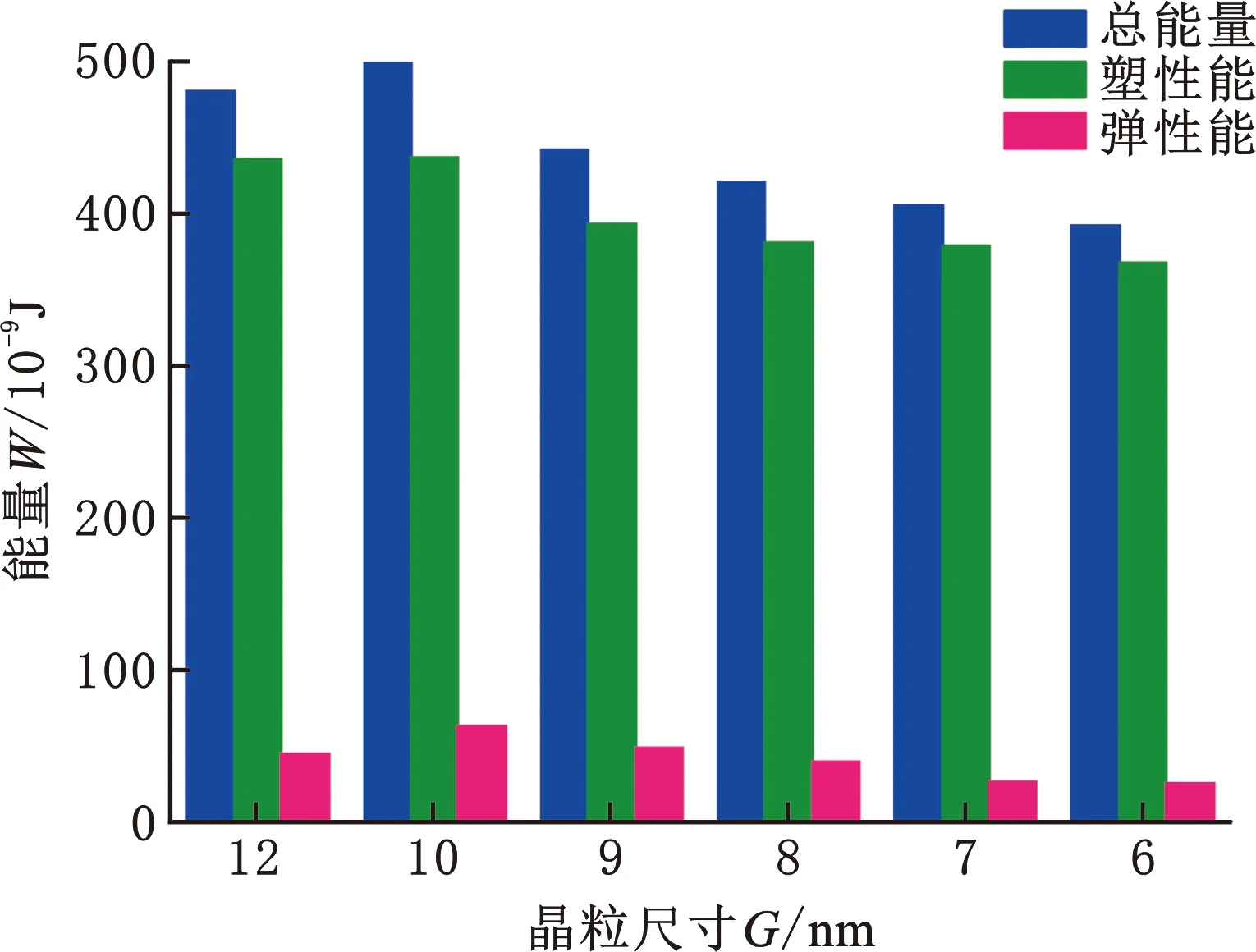
图6 不同晶粒尺寸条件下总能量、弹性能、塑性能的对比Fig.6 Comparison of total energy，elastic energy，and plastic energy under different grain sizes

残余深度hf的大小可反映压头在接触过程中基体塑性变形的程度以及分离过程中弹性回复量的大小。采用Alpha-shape算法[31]对卸载后的多晶铜基体表面形貌进行拟合，得到分离接触后的基体表面形貌，如图7所示。

(a)G=12 nm (b)G=10 nm

通过式(4)和式(6)计算得到的不同晶粒尺寸下多晶铜的纳米硬度以及接触刚度见表 2。由表 2可知，当某一晶粒尺寸条件下的残余深度hf相对越大，则该晶粒尺寸对应的多晶铜的纳米硬度Hp相对较小，接触刚度S相对较大。

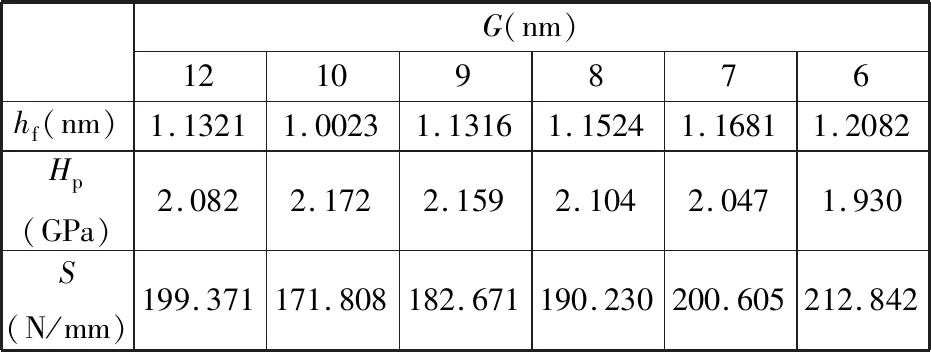
表2 不同晶粒尺寸条件下残余深度、纳米硬度、接触刚度计算值Tab.2 Calculated values of residual depth，nano-hardness，and contact stiffness under different grain size conditions

接触刚度S是表征材料抵抗弹性变形能力的指标。由图8a和图8b可以看出，随着晶粒尺寸的变化，接触刚度S与弹性能We成负相关。这是由于弹性能We是基体在弹性变形中所储存的能量，弹性能越大，表明弹性变形量越大，材料抵抗弹性变形的能力越弱，接触刚度越低。纳米硬度Hp反映了材料抵抗局部塑性变形的能力。从塑性变形的本质来说，位错的产生及滑移是出现塑性变形的主要原因。塑性能Wp表示在外载作用下晶格畸变以及位错滑移所产生的所有畸变能之和。然而，当晶粒尺寸为纳米级(小于10 nm)时，晶粒中可存在的位错极少，位错塞积强化效应不再适用，因此导致纳米硬度Hp与塑性能Wp成正相关，如图8c和图8d所示。综合图8b与图8d可知，纳米硬度Hp与接触刚度S的变化总体成负相关。当晶粒尺寸为纳米级时，纳米硬度越小，接触刚度越大。

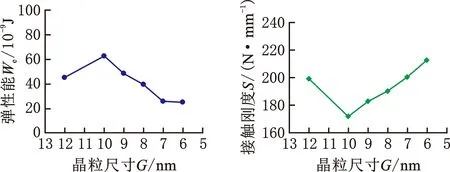
(a)弹性能随晶体尺寸变化情况 (b)接触刚度随晶粒尺寸变化情况

2.3 多晶铜亚表面变形机理

为研究多晶铜基体在接触过程中的弹塑性变形过程，采用公共近邻分析(common neighbor analysis,CNA)方法分析了多晶铜基体在与金刚石压头弹塑性接触过程中位错的形核以及扩散规律。图9所示为不同晶粒尺寸条件下各多晶铜基体的弹塑性变化过程，从左至右依次为金刚石压头压入多晶铜基体的深度h=0、0.3 nm、0.5 nm、1.0 nm、1.5 nm和2.0 nm时基体的内部原子结构形貌。图中的深蓝色原子代表晶界原子，浅蓝色原子代表具有正常FCC晶体结构的铜原子，绿色原子代表位错原子，橙色原子代表其他缺陷原子。由图9可以看出，随着压头与基体逐渐开始接触，当压头压入基体的深度h=0.3 nm时，基体上靠近压头正下方的部分区域开始出现位错形核，如图9中红色箭头所示；并且随着压头的持续压入，基体内萌生的位错开始沿着晶粒的{111}滑移系滑移扩散。当压入深度较小时，位错的滑移运动会受到晶界的阻碍，表现为运动到晶界的位错会被晶界吸收，如图9中黄色箭头所示；当压入深度逐渐增大时，部分晶界位置会不断地累积内应力以及原子势能，而当累积到一定程度时，部分位错会在晶界附近形核并穿过晶界继续滑移扩散，从而使得塑性变形过程持续进行，如图9中粉色箭头所示。

(a)G=12 nm

由图9还可以看出，较小晶粒尺寸的多晶铜拥有数量较多的晶界，由于晶界具有较大的弹性应变能，因此位错的运动会被约束在压头周围的若干晶粒中，导致较小晶粒尺寸的多晶铜的位错分布范围较小，产生的位错较少。由此导致位错塞积强化效应的不适用，使得具有较小晶粒尺寸(小于10 nm)的多晶铜材料的纳米硬度相对较低、接触刚度相对较大。

3 结论

(1)不同晶粒尺寸下，多晶铜黏着接触过程中，最大黏着力基本保持不变。最大法向接触力随晶粒尺寸的减小表现出先增后减的趋势。

(2)纳米硬度和接触刚度分别与接触与分离过程中的塑性能和弹性能的变化相关，且纳米硬度与接触刚度变化总体成负相关。

(3)晶粒尺寸越小的多晶铜拥有数量相对更多的晶界，晶界数量会对材料的纳米硬度产生影响，进而影响其接触力学特性。