运动想象脑电信号特征提取与分类的黎曼方法研究*

高诺，高志栋，张慧，陈鹏程

(山东建筑大学信息与电气工程学院，济南 250101)

1 引 言

脑机接口(brain-computer interface, BCI)技术是在人的大脑与计算机或其它外部设备之间建立的直接交流和控制通道，借助该通道人不需要语言和动作就能让大脑表达想法、操作设备。对患有严重身体障碍的患者，利用BCI技术能够让他们与外界进行无障碍交流，从而改善生活质量、减轻家庭负担[1]。在脑机接口技术中，较为常用的采集大脑信号的方式是头皮脑电图(electroencephalogram, EEG)，EEG信号主要采集自头皮，是非侵入式的，且完全无创，是在所有大脑电信号采集方式中最为简单和安全的[2]，因此，其被广泛应用于脑机接口技术中。

在脑电信号采集过程中，信号经过人脑组织的层层传输使得其强度逐渐减弱、空间分辨率和频率范围也受限，同时受外部环境的多重影响，导致采集到的EEG信号噪声较大，信噪比较低[3-4]。目前EEG信号处理算法的精度与准确率等均无法满足BCI技术的应用要求，因此EEG信号有效的分析与处理算法的研究一直是BCI技术的研究难点与热点。

传统的EEG信号分析与处理算法大多存在于欧式空间，一般包含特征提取与分类器分类两个部分。在特征提取部分，共空间模式(common spatial pattern, CSP)方法使用最为广泛[5]。其通过设置空域滤波器对脑电信号空间分布进行处理，提取可分类的特征，旨在得到一个最大化两类分类任务信号方差的最优空域滤波器，进而从脑电信号中提取最为可分的特征[6-8]。在分类器方面，许多机器学习领域中高效的分类器都可以直接应用到脑机接口中，比如支持向量机(support vector machine, SVM)[9]、线性判别准则(linear discriminant analysis, LDA)[10-11]等。

然而仅体现各个通道信号的时、频信息的传统欧式空间的特征提取和分类方法已无法满足精确刻画大脑活动的要求。近几年出现的基于黎曼空间的信号分析方法在睡眠脑电、癫痫脑电特征提取与分类方面取得了较为显著的效果[12]。随后逐渐有学者开始进行脑机接口技术中EEG信号的黎曼空间方法研究。2012年，Barachant等[13]提出了最小黎曼均值法(minimum distance to Riemannian mean, MDRM)和切线空间的线性判别准则法(tangent space LDA)，均取得了不错的分类效果。2018年，Zanini 等[14]提出了基于黎曼几何空间框架的迁移学习方法，其验证算法就是MDRM算法。

尽管基于黎曼空间的EEG信号分析与处理方法效果显著，但由于该方法的研究起步晚，还有很多问题亟待解决，例如，MDRM方法中需要进行黎曼均值的计算，目前针对黎曼均值的计算均需迭代计算，尚无解析计算方法[13]。该计算方法不仅计算精度无法保障，同时由于耗时较大，影响了其在在线BCI技术中的应用。另外，目前将EEG信号从欧式空间转移到黎曼空间均是采用了信号的协方差矩阵，该转换方法无法体现EEG信号中的频率变化，影响了信号分析的性能。

针对上述问题，本研究提出了基于功率谱密度矩阵(power spectral density , PSD)的EEG信号特征提取与分类的黎曼空间方法，并且采用BCI竞赛数据进行了验证，结果表明，本研究基于功率谱密度矩阵的黎曼空间分析方法可以有效进行运动想象脑电信号的分类，分类精确度较高，耗时较少。

2 系统方法

本研究提出的基于PSD矩阵的EEG信号特征提取与分类的黎曼几何方法的整体结构，见图1。该算法的大体流程为：对大量已知类别的EEG信号分别计算其相应的PSD矩阵，并按照类别构建相应的PSD矩阵集。PSD矩阵的建立完成了EEG信号从欧式空间到黎曼空间的转换。针对一个未知类别的EEG信号，计算其PSD矩阵并计算该PSD矩阵与不同类别PSD矩阵集中所有PSD矩阵之间的黎曼距离。最后利用KNN算法计算未知类别EEG信号的类别归属。

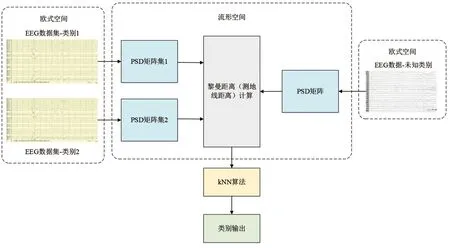
图1 基于PSD矩阵的EEG信号黎曼几何方法结构框图

2.1 PSD矩阵建立与计算

通常情况下，收集的脑电数据一般是M个通道的信号，时间可能长达数小时。EEG信号是非平稳的，但是为了更好地把每一类运动想象信号分辨出来，需要将数据按T秒分离开，即每一次运动想象都是以T为时间单位的M个通道的数据。有理论研究证明，如果T≤30 s，那么每一次EEG信号周期都可以看作是广义平稳信号[15]。由于本研究所用的EEG信号周期T均小于30 s，因此，本研究中可以将其看作广义平稳信号。

2.1.1EEG信号 根据前面的阐述，对于某位受试者，收集所有M个通道的信号数据并将这些多通道数据的第n个周期表示为矢量：

sn(t)=[sn1(t),…,snM(t)]T,t=0,…,T-1

(1)

因此，该受试者的第n个周期数据矩阵由下式给出：

(2)

然后，用其Frobenius范数对每个周期的EEG数据进行归一化[27]，归一化后的数据矩阵为：

(3)

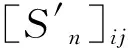
(4)

其中，ιn∈{1,2,…,L}，它表示属于L个运动想象EEG信号的第n个周期的类标签。

2.1.2PSD矩阵估计 由前文可知，EEG信号可以看作广义平稳过程，由数学理论获得，广义平稳过程的功率谱密度函数和自相关形成傅立叶变换对[16]。对于第n个周期的多通道脑电信号矩阵，其列向量为M个通道的脑电信号见式(1)，且可以看成是广义平稳向量。因此，其集合平均值与协方差可以通过对时间进行平均而得到：

(5)

Rn(τ)=E[{sn(t+τ)-μn}{sn(t)-μn}T]

(6)

其中，协方差矩阵Rn(τ)是半正定的矩阵。若Rn(τ)的l1范数和为有限值，则对Rn(τ)进行离散傅里叶变换，就可以得到信号在频率ω处的Hermitian正定PSD矩阵：

(7)

理论上讲，式(7)中时间τ的大小应该在(-∞,+∞)。而在实际信号处理过程中，由于样本数量有限，一般限定τ∈[-(T-1),T-1]。同时可以在频率范围[ωmin,ωmax]内选择任意频率ω=ωi计算相应的PSD矩阵Pn(ωi)。

为了从有限的脑电数据中获得功率谱密度矩阵，需要对协方差矩阵进行估计，而协方差矩阵的无偏估计可能无法正定。若使用有偏估计可以保证正定性，但如果数据记录较短，则可能会降低频谱分辨率，并且偏差可能会变得过大。本研究采用Nuttall-Strand算法进行功率谱密度矩阵的估计。该算法使用前向-后向线性预测来迭代估计残差协方差矩阵，从而获得具有高分辨率的功率谱密度矩阵的精确正半定值[17]，该估计值可作为脑电信号的功率谱密度特征。

2.2 PSD矩阵的黎曼距离计算

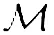
在频率范围[ωmin,ωmax]内，一段脑电信号的正定PSD矩阵可以表示为流形内参数为频率变量ω的一段曲线。对于同样的频率范围[ωmin,ωmax]，第n与第m个信号周期的两个特征PSD矩阵可以分别表示为Pn(ω)和Pm(ω)，见图2。在相同频率时，两条曲线上的两个点Pn(ωi)和Pm(ωi)之间的距离定义为黎曼空间中自由点之间的距离。

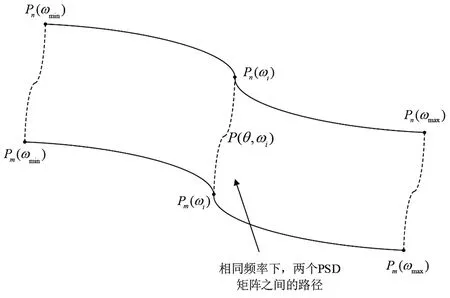
图2 PSD矩阵的空间分布及距离

连接两个点Pn(ωi)和Pm(ωi)的路径会随参数θ的变化而变化，因为该路径变化的上限是m，下限是n，因此，可以定义θ∈[θm,θn]。则在频率ω=ωi时，路径变化上限是Pm(θm,ωi)，下限是Pn(θn,ωi)，因此，两点之间的路径可以定义为：

(8)

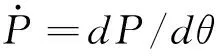
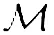
(9)

式(9)为在黎曼空间中两点之间的测地线的距离计算公式，然而其很难得到一个闭合的解，因此，使用式(9)直接计算黎曼距离很困难。

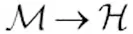
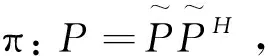
(10)

基于纤维束理论的黎曼距离的计算方法能够对黎曼距离进行直接求解，避免了迭代求解方法中存在的收敛速度慢、计算时间长等问题，为基于黎曼空间的脑电信号分析与处理算法在脑机接口技术中的应用提供了理论基础。

推导出黎曼空间中两条曲线上自由点之间的距离后，本研究采用信号频率范围内黎曼距点累加和作为两个PSD矩阵间的相似性/非相似性度量，并将此度量用于后续分类算法。

2.3 KNN分类算法

KNN算法是数据挖掘技术中的经典分类方法，其工作原理是计算被分类对象与训练数据集的距离，然后对距离进行升序排序，选出其中k个最近的邻居(即距离最小的k个)，最后根据这些邻居的分类标签进行判断，将得出的标签分配给被分类对象的分类属性[19]。

理论上讲，k的选择并没有一定的选择原则，如果样本数量是无限的，那么k的选择越大则分类效果越好[20]。但由于在实际实验中，样本数量是有限的，因此k的选择不可能达到无穷大。在有限样本的情况下，应实现较小的k也能达到较为满意的分类效果。

3 实验数据与结果

本研究分析的数据来自于2008年BCI竞赛数据集1。该数据集包含7位受试者(s1-s7)的两种不同种类的运动想象脑电数据。每位受试者分别进行想象左手运动100次和想象右手运动100次，运动想象时序图，见图3。为了验证基于黎曼空间方法的有效性，选取受试者数据中的160次(包含80次想象左手运动和80次想象右手运动)作为训练数据集，剩余40次运动想象数据作为测试数据集，从三个方面阐述本研究算法的有效性。

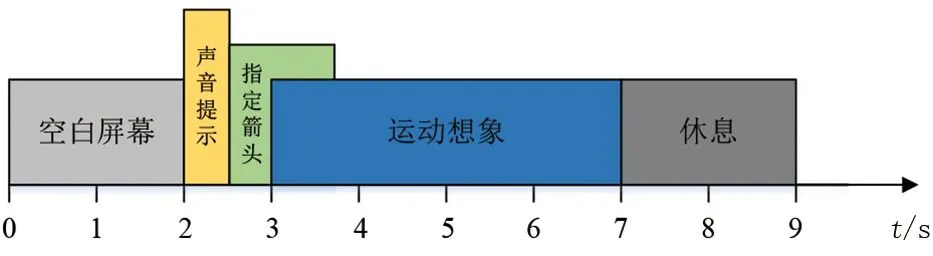
图3 竞赛数据运动想象时序图

3.1 k的选择对分类准确率的影响

KNN算法中，k的选择会直接影响分类准确率，同时受样本数量的影响。针对此问题，我们研究了在小样本数量(160个运动想象数据的训练集)下，k的变化对分类准确率的影响。在验证过程中，选择了两种距离度量方式，一种是黎曼距离，另一种是欧式距离。图4是在两种距离度量下，受试者3(s3)在不同k的选择下的分类准确率的变化曲线。

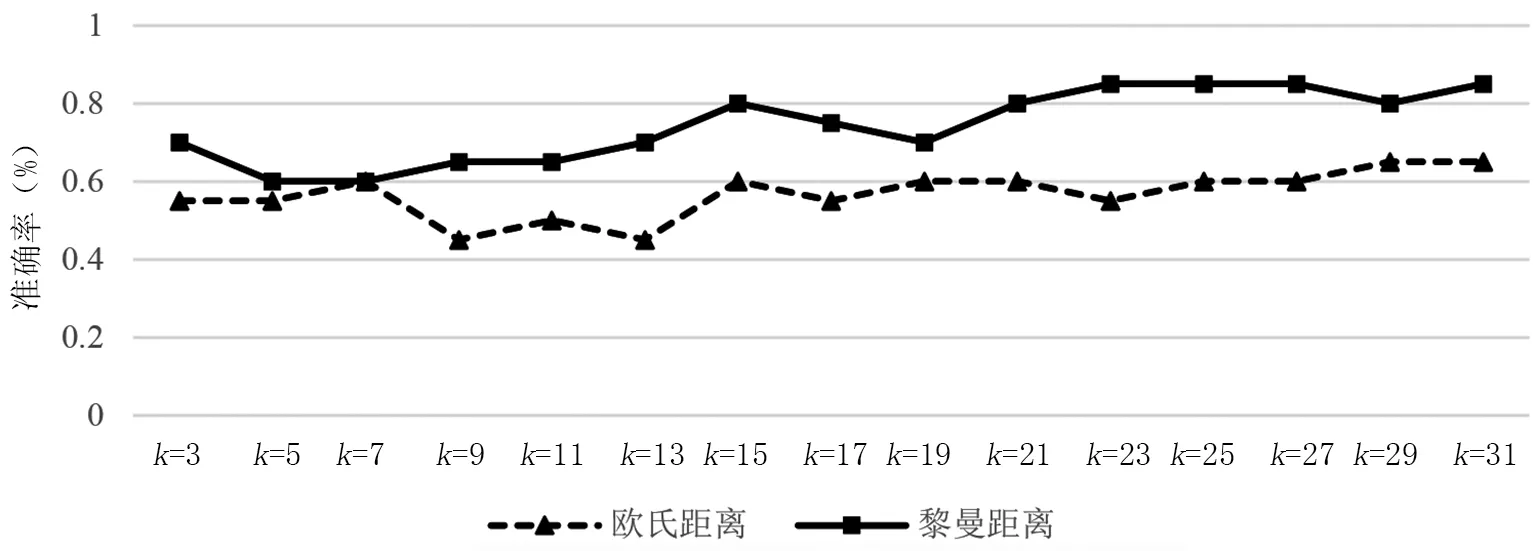
图4 欧式与黎曼距离分类准确率对比

由图4可知，无论k如何变化，欧式距离下的分类准确率总是低于黎曼距离下的分类准确率。说明以PSD矩阵作为脑电信号特征的黎曼空间算法，黎曼距离是更加合适的相似性/非相似性度量。

图4中，k的最小值为3，最大值为31，可以看出，随着k的增大，无论是欧式距离下的分类准确率还是黎曼距离下的分类准确率都呈现逐渐上升的状态，当k大于20后，上升的趋势逐渐趋缓，黎曼距离下的分类准确率稳定在80%以上，欧式距离下的分类准确率稳定在60%以上。由此说明，虽然理论上在样本集数量固定的情况下，k的选择是越大越好，但是在样本有限的情况下，较小的k也能达到较为满意的效果，这也是KNN算法的优势之一。

3.2 与MDRM方法的对比结果分析

如前文所述，MDRM方法是目前应用较为广泛的黎曼空间脑电信号分析算法。该算法在训练阶段需要对所有已知分类的脑电信号进行黎曼均值的计 算，由于目前尚无黎曼均值的解析求解方法，需要使用梯度下降算法进行迭代实现，因此，该算法在训练阶段较为耗时，同时无法保证迭代的收敛性与计算精度。本研究将所提算法与MDRM算法在训练阶段所需时间进行了对比分析，分析结果见图5。

由图5的对比结果可知，针对7位受试者，本研究方法在训练阶段所需时间均低于MDRM算法，且所需时间比较稳定，均保持在1.5 s左右。而MDRM算法对不同受试者的训练时间差异性较大，从2.89 s(s1)到16.47 s(s6)不等，该差异性显示了黎曼均值算法的不稳定性，直接影响MDRM算法的分类精度与应用性。

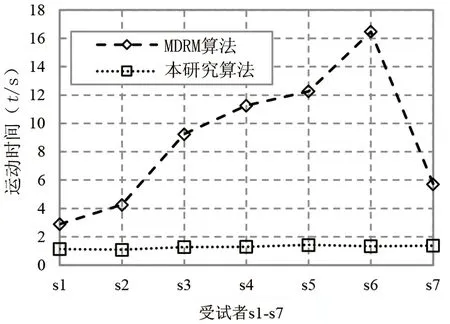
图5 MDRM与本研究算法所用运行时间对比

图6是两种方法针对7名受试者的运动想象数据的分类准确率对比图。由图6可知，受试者s6使用MDRM算法的准确率优于本研究算法，而其余6名受试者，本研究算法的准确率优于MDRM算法，其中在s2、s4、s5与s7中，本研究算法优势较为明显。

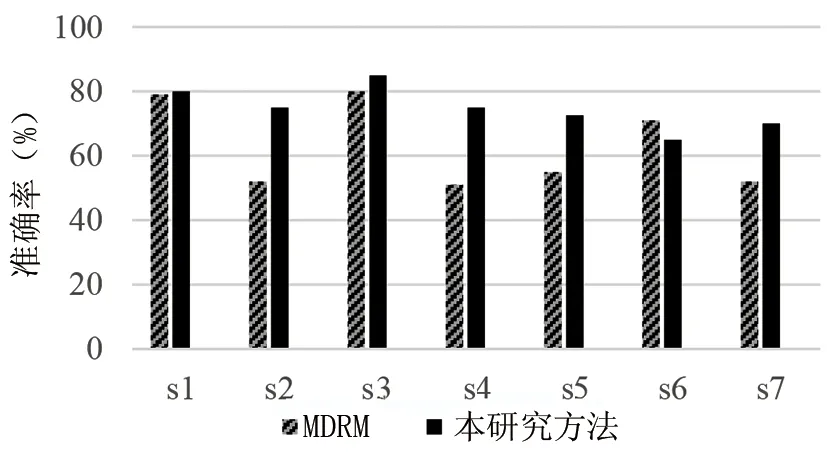
图6 MDRM与本研究算法的分类准确率对比

3.3 与经典算法的对比结果分析

本研究将所提算法与传统经典脑电信号特征提取与分类算法(CSP+SVM，小波+SVM)的分类结果进行了对比分析，不同方法的分析准确率见表1。

由表1中的数据可知，针对7位受试者，本研究方法的平均准确率较另两种方法分别高出24.17%和12.14%。较高的分类准确率显示了本研究方法在运动想象脑电信号分类中的优势，也说明基于黎曼空间的脑电信号分析方法更能够体现不同大脑活动脑电信号之间的差异。同时，针对不同的受试者，相同的分类方法其分析准确率差异性较大，体现在分类准确率的标准方差均在5%以上。这种差异性来自于不同受试者的个体差异、实验过程中的环境噪声与心理状态的变化。

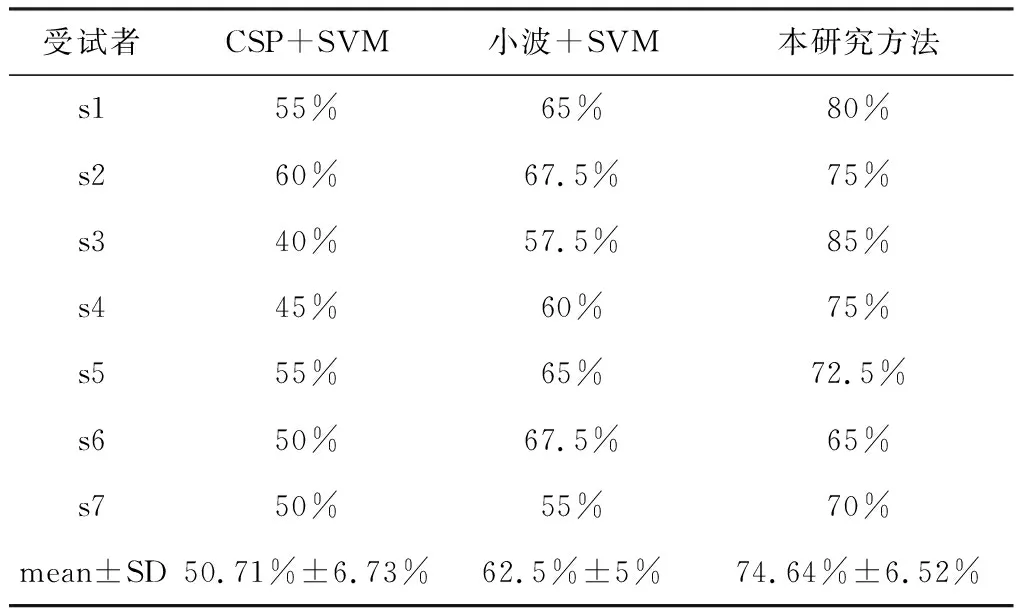
表1 本研究方法与经典方法准确率对比

4 结论

针对目前脑电信号分析与处理算法无法满足脑机接口技术的应用要求的问题，本研究提出了一种基于黎曼空间的运动想象脑电信号特征提取与分类方法。该方法以脑电信号的PSD矩阵作为特征，以黎曼距离度量脑电信号之间的相似性/非相似性，以KNN算法作为最终的分类方法对不同运动想象脑电信号进行黎曼空间的分析与处理。为了验证该方法的可行性与有效性，本研究进行了一系列的相关实验，实验结果说明，本研究方法可以在样本集数量较小的情况下对运动想象脑电信号进行分类，分类方法具有较高的分类准确率、较小的计算量和较快的计算速度。