考虑波长因素的高铁无砟轨道不平顺分形分析

吴鹏飞，李再帏，刘晓舟，何越磊

(1. 上海工程技术大学 城市轨道交通学院，上海 201620；2. 深圳技术大学 城市交通与物流学院，深圳 518118)

轨道不平顺是指轨道几何位置相对于轨道初始设计位置的偏差，其偏差值主要是通过轨检车动态检测来采集的[1]。轨道不平顺是引起轮轨振动的主要原因，其幅值与波长的分布特征是影响列车运行速度、安全性以及乘客舒适性的重要因素[2]，因此，深入挖掘轨道不平顺的波长分布特征，实现波长的定量化评定具有显著的现实意义。目前，许多学者采用不同的研究手段从时域、频域以及时频域等角度对轨道不平顺状态进行了刻画，形成了TQI，功率谱及时频能量谱的管理方法。但随着线路运营速度的不断提高，轨道几何幅值超限问题极少发生，为了深刻地表征无砟轨道不平顺状态，国内外学者引入了分形理论进行轨道不平顺的分形特征研究，HYSLIP[3]采用分形尺码法计算有砟线路高低不平顺的分形维数，利用分形维数对不同波段的轨道几何状态进行评估；LANDGRAF 等[4]结合欧盟相关标准，将轨道不平顺波长分成短波、中波和长波3类，同样采用分形维数进行定量化表征；TACIROĞLU 等[5]对土耳其某高铁线路轨道不平顺数据进行分析，采用4种不同的分形维数来表征轨道短波和中长波不平顺。陈光雄等[6]利用分形功率谱法对摩擦面波状磨耗进行定量化的计算，得出分形维数能够定量描述摩擦面的波状磨耗。这些研究极大地深化了对轨道不平顺细部特征的认识，提供了定量化评价轨道不平顺波长和状态的途径。但同样值得注意的是，目前，对于我国高铁无砟轨道不平顺的分形特征尚无针对性研究，分形维数定量化评定我国高铁无砟轨道不平顺波长特征的能力需要进一步分析。基于此，本文从分形几何的基本原理出发，利用蕴含波长特征的分形尺码法，计算我国高铁无砟轨道不平顺的分形维数，分析无砟轨道不平顺波长的分形维数表征，为进一步研究分形维数评估无砟轨道几何平顺状态奠定技术基础。

1 分形几何基础

1.1 分形原理

分形是指一种复杂性高且无法用传统的欧氏几何来描述，但其局部与整体在形态、功能、时间及空间具有一定自相似的图形和集合的总称[7]；分形的基本属性是自相似性、标度不变性和分形维数[8]。自相似性和标度不变性通常是判断对象是否可以利用分形理论对其进行分析的重要指标。分形维数表征了充满空间的能力，是定量描述分形对象复杂程度和不规则性的参数，其既可以是整数也可以是分数。自然界中的分形与数学分形相比，其自相似性并不是严格意义上的自相似，而是统计意义上的自相似；另外，其分形特征只存在于有限的层次范围内而非无限层次范围内。这是自然界中的分形与数学分形的根本差别所在，也是导致分形维数测量不稳定的根本原因[9]。目前，计算分形维数的方法主要有尺码法、盒维数法、结构函数法等，其中尺码法是轨道几何形位评价中应用较为有效的方法[3-5]，此方法的突出特点是可以定量化地确定轨道不平顺波长特征。因此，本文采用尺码法进行高速铁路无砟轨道不平顺分形维数的计算。

1.2 尺码法原理与计算流程

尺码法源于海岸线长度测量问题，根据Man‐delbrot的理论[10]，尺码与测量长度之间具有明显的幂律关系：

等式两边同取对数为：

式中：δ为尺码长度，其为无量纲量；N为测量曲线所需的尺码段数；R(δ)为利用尺码δ测量曲线所得的长度；D为曲线的分形维数。

采用不同的尺码δ去测量曲线会得到不同的R(δ)，小尺码δ测得的曲线长度R(δ)较大，大尺码δ测得的曲线长度R(δ)则较小。当得到多组(δ，R(δ))数据之后就可以利用式(2)在双对数坐标系中绘制出一系列的点，利用最小二乘线性回归可得到回归直线的斜率k，则k与D关系如下：

上述为尺码法的原始定义，而在实际测量分形维数中，尺码的形式较为多样，不局限于一定长度的线段，也可采用圆形、正方形及长方形等形式[11]。

尺码法的算法流程如下。

Step 1：确定度量的初始尺码，按照式(4)进行取值[12]：

式中：a0为初始尺码；N为数据点数；i=1,…,N−1；ki为曲线上相邻2 个数据点之间的欧氏距离，x，y分别为数据点的横纵坐标。

Step 2：以曲线的起始数据点为尺码的起点，以a0为初始尺码跟踪曲线的数据点，若尺码的端点位于相邻2个数据点之间，则端点值由三角函数插值和相似定理求出。当尺码测量至曲线末端时，最后一段尺码末端不一定和曲线的末端相重合，需要将计算剩余的曲线长度与测量的曲线长度相加。Step 3：当尺码测量至曲线末端时，将测量的尺码段数乘以尺码加上剩余的曲线长度即可得到该尺码下测量曲线的总长度，计算公式如下：

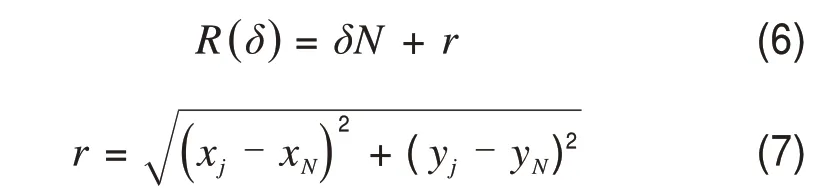
式中：(xj,yj)为尺码末端点的坐标；(xN,yN)为曲线末端点坐标；R(δ)同前；r为剩余的曲线长度。

Step 4：采用不同的尺码测量整个曲线，为了抵消线性回归带来的误差，每一次测量的尺码长度应为a0←2*a0[13]；记录下每次测量完曲线的总长度R(δ)和尺码长度δ，在双对数坐标系中绘制出数据点，采用最小二乘线性回归可得到回归直线的斜率k，利用式(3)即可求得曲线的分形维数D。

2 轨道不平顺波长分形维数特征

2.1 尺码法的测量过程及结果分析

本文利用Matlab 软件实现上述算法，由于轨道不平顺已被验证具有典型的统计自相似分形特征[3−5]，因此，这里利用尺码法对我国高速铁路无砟轨道不平顺的分形维数进行分析。数据来源为某300 km/h高铁线路，轨道结构类型为CRTS Ⅱ型板式无砟轨道，轨检车型号为CRH380AJ-0203，采样间隔为0.25 m。利用左高低不平顺样本说明尺码法的整个测量过程，样本数据、测量过程及计算结果如图1～图3所示。

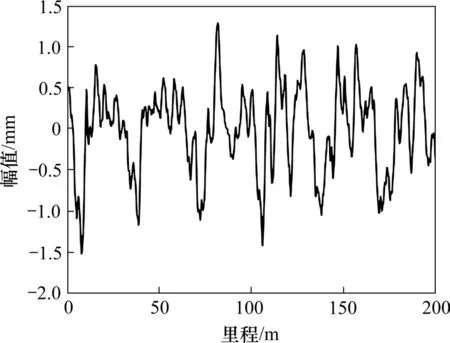
图1 样本数据Fig.1 Data of sample

由图2可知，随着波长尺码的逐渐减小，由尺码连接的曲线逐渐趋近于原始曲线，即较小波长尺码受原始波形短波长成分的影响较大，而较大波长尺码受原始波形中长波成分的影响较大[3]。

图2 测量过程Fig.2 Measurement process

图3为式(3)的具体计算结果，可知无砟轨道不平顺分形维数无法用单一的波长区段进行表征，其结果具有典型的分段函数特征，需要按照不同波长区段进行分形维数的计算。因此，本文将进一步地讨论不同波长区段下，轨道不平顺的分形维数特征。

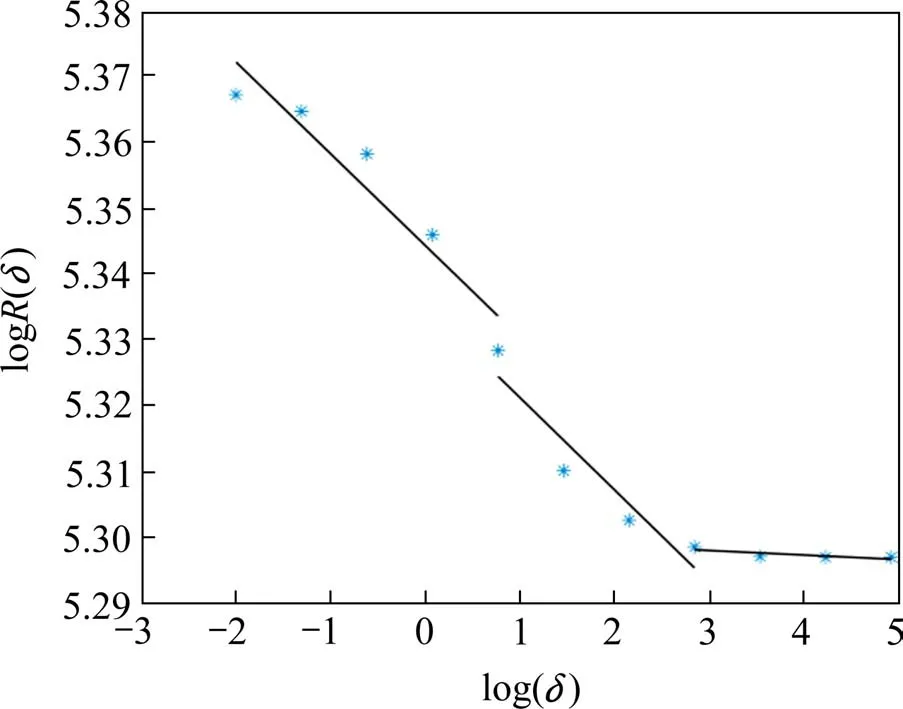
图3 测量结果Fig.3 Measurement results

2.2 单一波长的轨道不平顺分形维数特征

一般而言，轨道不平顺可以认为是典型的随机波形，是由无穷多个不同波长和幅值的正弦波叠加而成[14]，因此，单一波长的不平顺可表示为：

其中：A为振幅，控制幅值的大小；ω为角速度；λ为波长，其与角速度的换算关系式如式(9)所示。

根据文献所述，按照波长划分轨道不平顺，通常分为3 m 以下的短波不平顺、3 至30 m 之间的中波不平顺和大于30 m 的长波不平顺[15]。本文利用式(8)和式(9)得到幅值为1 mm，波长分别为2，10 和50 m 的轨道不平顺，采样间隔为0.25 m，样本长度为200 m，采用尺码法分别进行计算，结果如图4所示。

由图4 可知，分形维数结果可分为D1，D2和D33 个区段，其中2 m 波长对应的分形维数D1较大而D2和D3几乎没有变化；10 m 波长对应的分形维数D2较大而D1和D3几乎没有变化；50 m 波长对应的分形维数D3较大而D2和D3几乎没有变化；这说明分形维数D1，D2和D3分别表征了轨道不平顺的短波、中波和长波成分，可以利用分形维数对轨道不平顺的波长特征进行针对性管理。

图4 单一波长的轨道不平顺及计算结果Fig.4 Track irregularities of a single wavelength and calculation results

3 实例分析

本节选取长度为200 m 的左、右高低和左、右轨向不平顺数据样本作为分析对象，数据来源同前，利用尺码法计算样本数据的分形维数，结果如图5所示。

由图5可知，左、右高低不平顺分形维数的D2较D1与D3值大，说明左、右高低不平顺中虽然存在一定的短波长和长波长成分，但中波长成分占据了主要地位。左、右轨向不平顺分形维数的D1，D2值较大，D3则接近于水平直线，说明存在较多的短波长成分和少量的中波长成分，长波长成分则很少。本文同样给出了高低与轨向功率谱和标准谱的计算结果，高低不平顺中波长区段曲线远高于中国无砟轨道不平顺标准谱，验证了分形维数的计算结果，同理，轨向不平顺功率谱结果与分形维数对应也较好。所以，可以采用分形维数指标对轨道不平顺区段波长进行定量化评定管理。

图5 实测不平顺样本及计算结果Fig.5 Samples of measured irregularities and calculation results

在此基础上，本文对同前线路全线约140 km的左、右高低及轨向不平顺数据进行分析，将其按照200 m 切分，共分成700 组，讨论其波长尺码的稳定性，结果如图6所示。

图6 700组不同不平顺样本的尺码长度Fig.6 Sizes length of 700 samples of different irregularities

由图6 可知，对轨道不平顺进行分形维数计算，共有11 种不同的波长尺码，且波长尺码的波动性较小，仅在一个小范围内波动，为了进一步的对比分析，将图6波长尺码进行均值化处理，结果如图7所示。可以确定3段分形维数D1，D2及D3所对应的固定尺码分别为(0.135～2.16)，(4.32～17.28)和(34.56～138.24)。所以，可利用波长尺码计算不同样本的轨道不平顺分形维数，进而实现对轨道不平顺波长区段的定量化评价。

图7 不同样本的尺码长度平均值Fig.7 Average size length of different samples

4 结论

1) 分形维数可以有效地表征高速铁路无砟轨道轨道不平顺的波长分布特征，可以将其分为3个波长区间，即D1为(0.135～2.16 m)，D2为(4.32～17.28 m)，D3为(34.56～138.24 m)。

2)分形维数对应波长尺码具有较好地稳定性；采用分形维数指标可以有效地对区段轨道不平顺的波长进行定量化的评定，建议在此基础上进一步研究分形维数表征轨道几何平顺状态的能力，为现场养护维修作业提供有效的指导。