基于人工蜂群算法的桥梁有限元模型局部刚度修正

唐煜，岳杰，华旭刚

(1. 西南石油大学 土木工程与测绘学院，四川 成都 610500；2. 湖南大学 风工程与桥梁工程湖南省重点实验室，湖南 长沙 410082)

梁单元是一种空间上三维或二维而几何上一维的基本单元，宏观梁单元模型无法直接模拟结构细部，对实际桥梁结构在构件连接处因构造原因导致的局部刚度变化模拟失真，造成所谓的节点刚性区问题[1]。已有桥梁实测[2]、有限元仿真和模型试验结果[3]均表明局部刚度可显著影响桥梁结构的整体力学性能，在桥梁结构有限元建模时不应忽视局部刚度。为提高宏观梁单元模型中节点刚性区局部刚度的建模准确度，杨咏昕等[1]提出采用主从节点法和刚性材料法进行模拟，后者取得了二者中相对略好的模拟效果，但其中反应单元“刚性”提高程度的参数取值偏于主观，所得分析结果也与实际结构存在一些的差异，目前在桥梁结构有限元建模特别是用作动力分析的有限元建模过程中，对宏观梁单元模型的局部刚度模拟较为粗犷主观。模型修正是提高宏观梁单元模型准确度的有效途径。针对于桥梁结构，邹向农等[4]运用响应面方法并结合大桥特点选取一系列算法组合考虑了边界约束条件对悬索桥初始有限元模型的影响,并对其进行修正；马印平等[5]采用响应面法并基于一座钢管混凝土组合桁梁桥实测结果修正桥梁有限元模型；JUNG 等[6]采用遗传算法联合固有频率、振型和静态挠度对一座简支梁桥进行有限元模型修正；KANG 等[7]采用人工鱼群算法对某人行斜拉桥有限元模型进行了修正；刘海弯等[8]采用粒子群算法基于桥梁静载试验数据对桥梁有限元模型进行修正；TRAN-NGOC 等[9]采用粒子群算法和遗传算法对南澳铁路桥模型未知参数进行修正并对2 种算法优化修正效果做了比较；HA‐SANCEBI 等[10]利用人工神经网络方法并基于现场测试数据，以弹性模量和桥面质量对一座老化的T型梁桥梁有限元模型进行修正；韩万水等[11]提出了联合实数编码遗传算法与静动力实测数据的有限元模型修正方法。有限元模型修正的数学本质是优化问题，即利用模型计算值与结构真实值之间的误差建立目标函数，结合优化算法在修正参函数设计空间内，寻找使目标函数取最小值的修正参数值，达到模型修正的目的。人工蜂群算法(Ar‐tificial Bee Colony Algorithm, 简称ABC)是KARA‐BOGA[12]在2005 年提出的一种模拟蜜蜂蜂群智能搜索行为的生物智能优化算法，通过各人工蜂个体的局部寻优行为，最终在群体中使全局最优解凸显出来，是一种新型的全局优化算法。与迭代法、遗传算法、模拟退火算法、蚁群算法、粒子群算法等相比，人工蜂群算法在收敛性和收敛速度上均有一定优势[13]，已初步应用于桥梁颤振导数识别并表现出较好的稳定性[14]，但在桥梁模型修正领域还未见应用。为改善宏观梁单元桥梁结构有限元模型的建模准确度，本文提出基于人工蜂群算法优化节点刚性区局部单元刚度的模型修正方法。首先介绍人工蜂群算法基本流程，并以纯数学算例对算法的优化能力、收敛性和收敛速度做验证；随后以某刚构体系斜拉桥塔梁固结处的局部刚度修正问题为例，分别建立包含该节点刚性区的高维实体元模型和对应的宏观梁单元模型，对这2个层次模型开展同等条件下的静力分析和模态分析，以2模型间的模态频率误差和静力截面转角误差构造优化目标函数，再运用人工蜂群算法搜索节点刚性区内单元物理参数的最优解，据此实现模型局部刚度的客观合理修正，验证本方法的实用性和正确性。

1 人工蜂群算法

1.1 算法描述

人工蜂群算法是由蜂群采蜜行为启发的智能算法，将蜜蜂的采蜜过程转化为优化问题的寻优过程。蜂群包含3 个组成部分：雇佣蜂、跟随蜂、侦查蜂。雇佣蜂负责探索开发蜜源并将蜜源信息传递给跟随蜂，蜜源代表优化问题的一个解，而解的好坏用适应度函数评价；跟随蜂利用一种选择策略以一定的概率选择蜜源，然后在蜜源附近搜索新的蜜源；侦查蜂负责对被遗弃的蜜源进行随机初始化。算法实现的基本流程如图1所示。

图1 人工蜂群算法的基本流程图Fig.1 Basic flow chart of artificial bee colony algorithm

1.2 数值算例

为简要说明人工蜂群算法的搜索寻优能力，以常见的二次多项式参数拟合问题为例，比较人工蜂群算法寻优结果和最小二乘法拟合结果之间的差异。

根据二次多项式函数f(x)=ax2+bx+c构造一组样本数组，见表1。

表1 样本数组Table 1 Sample array

进行人工蜂群算法寻优时，根据数组建立如式(1)所示的优化目标函数

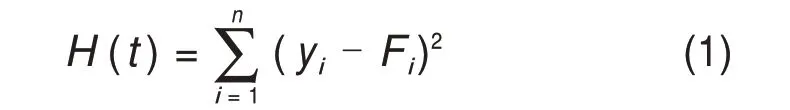
式中：t为以二次多项式中的3 个待定系数a，b和c为元素建立的优化参数向量；i为数组样本序号，此处取值范围为1～8；yi为数组样本值；Fi为优化系数后的二次多项式函数值。

在MATLAB 软件中写入人工蜂群算法迭代求解目标函数的最优函数值及对应的最优参数向量解，得到数组的拟合函数为y1= 1.158 27x2+0.802 78x+ 4.035 20。人工蜂群算法前30 次迭代优化过程如图2，可看出人工蜂群算法收敛速度较快。同样地，对该表1 样本数值做最小二乘拟合，所得拟合函数为y2= 1.158 27x2+ 0.802 80x+4.035 18。2 种方法的拟合函数系数几乎完全一致，函数曲线图高度重合(见图3)，表明人工蜂群算法具有较强的搜索寻优能力，可以用于多变量系统的参数优化。

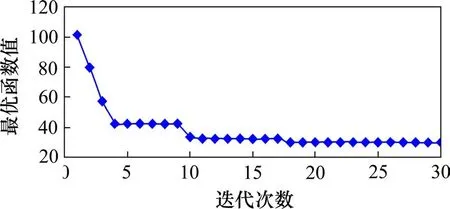
图2 人工蜂群算法寻优迭代过程Fig.2 Optimization iterative process of ABC

图3 寻优结果比较Fig.3 Comparison of optimization results

2 有限元模型修正理论

2.1 目标函数构造

宏观梁单元桥梁模型修正通过调整模型参数来减小模型数值计算值与结构响应真实值之间的差异，根据桥梁结构响应类型的不同，这些差异可体现在静、动力学等多个层面。定义模型修正目标函数为：

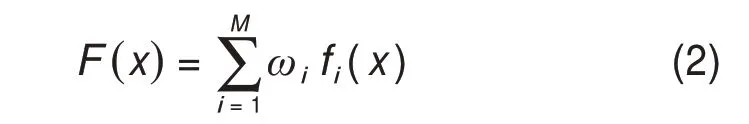
式中：x为待修正的模型参数向量；fi(x)为第i类结构静动力特性真实值与模型计算值之间的残差函数；M为模型修正中所考虑的结构响应类型总数；ωi为残差函数对应的权重系数。

用于有限元模型修正的结构真实值是相对的。一般认为实桥实测数据是最反映结构真实工作状态的，理想情况下最适合用做有限元模型修正，但实则不可避免地会受到实测环境干扰和实桥试验条件限制；试验室条件下的桥梁物理模型试验数据也能较好地充作结构相对真实值，但模型试验的缩尺效应难以妥善处理；在缺乏物理试验和实测数据的条件下，以更精细准确的高维实体元模型计算值作为结构响应的相对真实值，并据此开展宏观梁单元桥梁模型修正具有现实意义，尤其对设计阶段桥梁动力分析的建模准确度和求解效率提升均有积极意义。

以实体元模型计算值作为相对真实值来修正宏观梁单元模型局部刚度，为综合考虑模型修正后的静动力学性能，修正过程中联合了桥梁多阶模态自振频率和多个静弯矩荷载作用工况下的静位移转角计算值来构造目标函数

式中：fa(x)为截面转角残差函数；fb(x)为频率残差函数；N为实体元模型数值模拟静载试验的荷载工况数；gi(x)为第i类工况下的截面转角残差函数；n为转角的测点截面数；m为频率阶数；φti为实体元模型的第i阶频率值；φai(x)为梁单元模型的第i阶频率值；θti为实体元模型的第i个测点截面的转角值；θai(x)为梁单元模型第i个测点截面的转角值。

为保证模型修正结果有意义，目标函数需满足相应的约束条件，本文目标函数约束条件为

2.2 桥梁结构模型局部刚度修正流程

联合人工蜂群算法和实体元模型的静动力计算数据，对斜拉桥宏观梁单元模型节点刚性区的局部刚度进行修正，图4为具体修正流程：1)根据桥梁设计图纸截取包含节点刚性区的局部区域，分别建立实体元模型和对应的梁单元模型；2) 针对实体元模型进行动力特性分析和多个荷载工况下的静力分析；3) 选取模态频率和静响应位移建立目标函数；4) 在待修正宏观梁单元模型中选定修正参数；5) 启动人工蜂群算法进行寻优迭代，每次迭代后更新宏观梁单元模型中的修正参数。6) 当目标函数迭代残差小于预设的残差判据时迭代终止，模型修正完成。

人工蜂群寻优搜索过程在MATLAB 软件中进行，桥梁结构模态分析和静力求解在ANSYS 软件中进行，通过自编程序接口实现每个优化迭代步中人工蜂群算法各阶段的蜜源(优化参数)和结构静动力特征参数计算值(目标函数变量值)在2 个软件中的双向传递。

3 桥梁节点刚性区有限元模型

3.1 桥梁概况

某独塔斜拉桥设计方案采用塔梁固结的结构体系，总体布置图如图5(a)所示。在桥塔中心线两侧7.5 m 范围内，主梁为预应力混凝土箱梁结构，其余主梁为钢箱梁，塔根部主梁断面见图5(b)。主塔采用独柱式混凝土桥塔，上塔柱高92 m，采用箱型截面，壁厚渐变；下塔柱高25 m，截面为八边形空心台形，壁厚1 m，顶部与底部截面间采用直线过渡，塔柱断面见图5(c)。塔梁固结处为混凝土整体现浇，是典型的节点刚性区。

图5 独塔斜拉桥概况Fig.5 Overview of single-tower cable-stayed bridge

3.2 基于实体单元的局部有限元模型

本文重点研究塔梁连接处节点刚性区的等效梁单元模拟，故先基于实体单元建立区域模型以研究其力学特征。根据弹性力学的圣维南原理，在梁端部所施加外力的分布形式会影响外力作用处梁横向尺寸以内的内力分布。因此，为防止节点刚性区的静响应位移计算受到荷载局部效应的影响，所建立的实体元模型不仅应包括塔梁重叠的节点刚性区，还应包含足够范围内的塔、梁邻近区段。截取包含节点刚性区的桥梁局部建立实体元模型，作为后续开展静荷载响应分析和动力特性分析的基础。

该桥设计方案中主梁仅在距桥塔中心两侧7.5 m内为混凝土梁段而其余梁段均为钢箱梁段，由于本文旨在以提高塔梁结合部的模拟准确度为例介绍局部刚度修正方法，若对钢箱梁段也采用实体单元建模，不仅会增加建模难度，且会带来钢混结合面模型连接处理的新问题，对说明本文方法适用性实则无益。基于这种考虑，此处建模中将距桥塔中心两侧7.5 m 至41.4 m 范围内的主梁直接虚拟为混凝土梁段，其截面布置与桥塔附近混凝土梁段保持一致，桥塔下塔柱全部按设计高度建模，上塔柱截取12 m 高度范围进行建模。如此，则保证了梁端或塔端到塔梁结合部的距离大于塔梁截面最大横向尺寸的1.5 倍，可在该模型基础上开展静载求解和动力分析，间接研究塔梁结合节点刚性区的力学性能。在结构有限元软件ANSYS中使用Solid185 实体单元建立局部有限元模型，见图6。

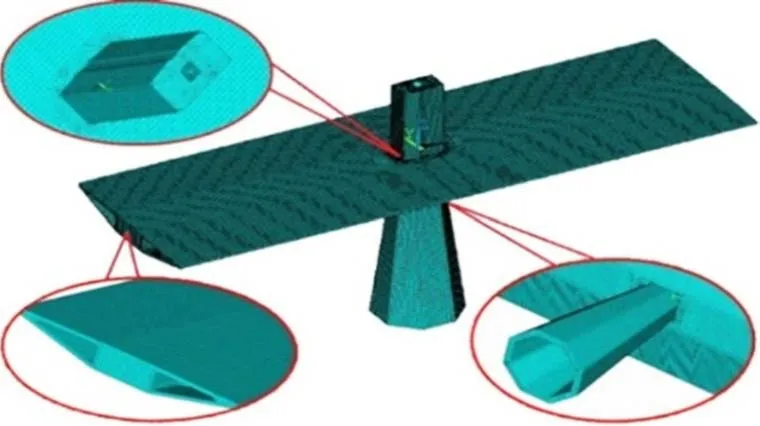
图6 实体单元模型Fig.6 Solid element model

3.3 基于梁单元的局部有限元模型

对照实体元局部模型，使用Beam44 单元建立局部有限元模型，其单元节点分布如图7所示。为便于模型修正且更真实反映刚性区的特性，根据塔梁几何重叠区域在梁单元模型中划分出节点刚性区。

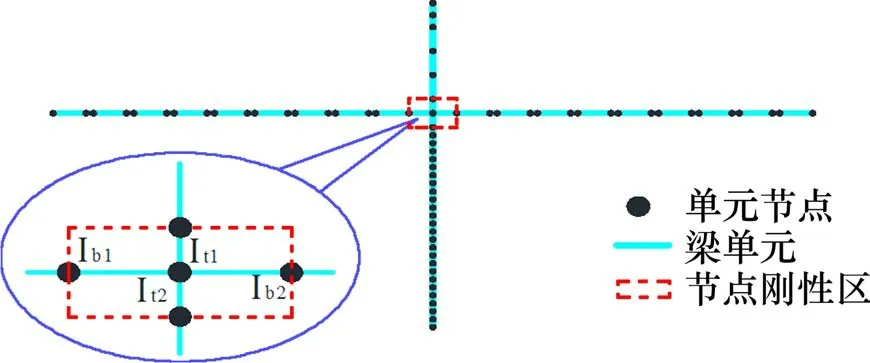
图7 梁单元局部模型及修正参数示意Fig.7 Beam element local model and correction parameters

梁单元局部有限元模型总共73 个梁单元，主梁划分40 个梁单元，其中包括刚性区内2 个单元，桥塔划分33 个塔单元，其中包含刚性区内2 个单元。由于塔柱截面变化，对上塔柱取6组截面不同的截面参数定义其截面变化，对于下塔柱取27 组截面参数定义其截面变化。

梁单元模型中的主梁单元为等截面特性，无法对主梁横隔板进行直接建模，导致梁单元模型与实体单元模型的总质量存在较大的误差(约为6.45%)。建模中，通过将梁单元模型中原属于横隔板范围内的梁单元材料密度适当放大，以考虑横隔板质量，即将密度乘以有横隔板节段与无横隔板节段的体积之比1.41，调整后的梁单元模型与实体单元模型质量差异为0.6%。对于主梁横隔板的刚度，在进行局部刚度优化修正前暂时无法考虑。

3.4 局部模型静动力特性

为了解节点刚性区对结构静动力响应的影响以保证模型修正结果的准确性，对实体单元模型和梁单元模型在同等条件下进行5种荷载工况下的静力分析，如图8 所示，My= 1× 106N ⋅m。各荷载工况下的上塔柱−梁顶面交接处、左梁−塔交接处静位移响应结果见表2。类似地，对实体单元模型和梁单元模型在同等条件下(塔底固结)进行自振动力特性分析，所得模态频率和振型如表3所示。

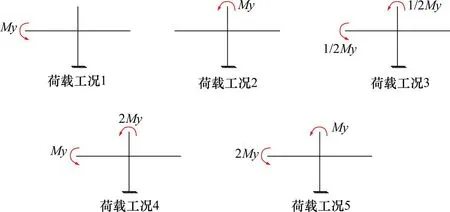
图8 荷载工况Fig.8 Load conditions

从表2 和表3 中可以看出，实体单元模型和梁单元模型的模态频率及5 种荷载工况下的上塔柱−梁顶面交接处、左梁−塔交接处截面转角均存在一定的差异。其中，主梁1阶竖弯模态频率误差较小为1.72%，2 阶和3 阶模态频率误差较大，分别为3.55%，5.23%；各荷载工况下的上塔柱−梁顶面交接处截面转角误差在3.44%～10.76%之间；荷载工况1 的左梁−塔交接处截面转角误差为16.23%，其余荷载工况下的梁端截面转角误差在4.77%～12.89%之间，节点刚性区对结构的静动力特性影响明显。

表2 局部模型的模态频率Table 2 Modal frequencies of local model

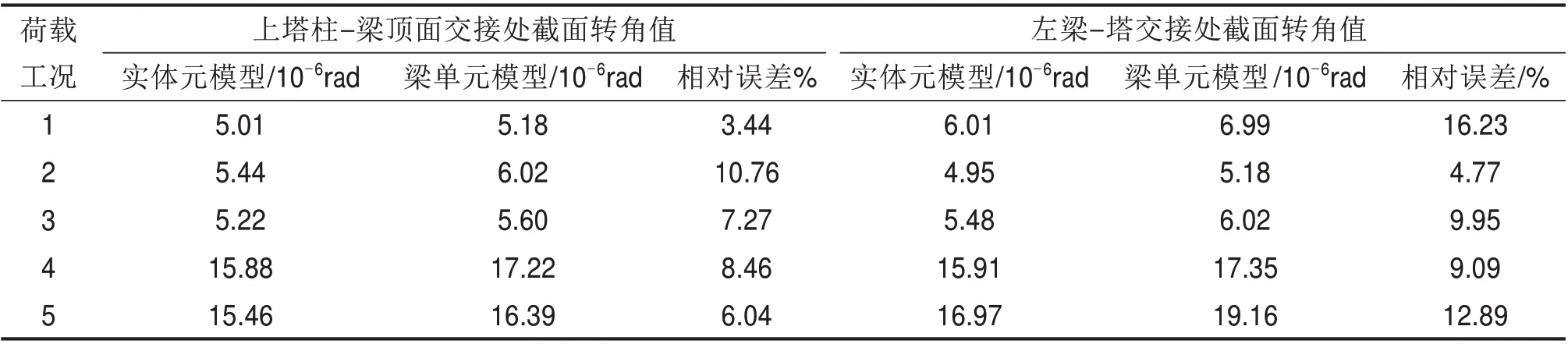
表3 各荷载工况下静位移Table 3 Displacements under static loads

4 宏观梁单元模型局部刚度修正

建立局部梁单元有限元模型时无法直接考虑横隔板的刚度影响，此处以单独主梁为对象，先对其横隔板处局部刚度进行修正，再在此基础之上对塔梁节点刚性区局部刚度进行修正。

4.1 修正参数选择

针对单独主梁而言，模型层次和横隔板刚度是影响其梁单元模型准确度的主要因素，对应的以弹性模量E，横隔板处的梁截面惯性矩Izz和Iyy作为可变参数来进行优化修正，并采用差分法进行了参数灵敏度分析，其端部转角敏度和频率灵敏度如图9所示。据每个修正参数的初始值并结合结构特点和实践经验设置各修正参数的取值范围，其中弹性模量E允许地调整范围为[3,4]×104，截面惯性矩Izz允许地调整范围为[1 000,3 000]m4，截面惯性矩Iyy允许地调整范围为[10,100]m4。

图9 单独主梁端部转角和频率灵敏度值Fig.9 Sensitivity of bending angle and frequency of girder

对于塔梁重叠区域，模型误差主要源自于梁单元参数无法合理描述节点交汇处因构件截面突变造成的局部刚度增强效应，此处针对4个刚性区内梁单元(见图7)选择8 个初始可变参数，包括节点刚性区域主梁的截面惯性矩Ib1zz，Ib1yy，Ib2zz，Ib2yy及桥塔的截面惯性矩It1zz，It1yy，It2zz，It2yy，同样采用差分法进行了参数灵敏度分析，其各测点截面转角灵敏度和频率灵敏度如图10 所示。图10 中，除It1yy，It2yy，Ib1yy，Ib2yy外其余参数的灵敏度值均很小，这与文献[1]桥塔塔柱−横梁节点刚性区有限元建模中建议只考虑桥塔平面内的刚度增强效应而不考虑桥塔平面外刚度增强一致，所以此处以It1yy，It2yy，Ib1yy，Ib2yy作为修正参数进行优化修正。根据每个修正参数的初始值并结合结构特点和实践经验设置各修正参数的取值范围，各个参数允许地调整范围均为[10,200]m4。需说明的是，单元截面积主要影响局部单元的轴向刚度，对于以梁单元受弯为主的桥梁结构模型，并无十分必要作专门修正。

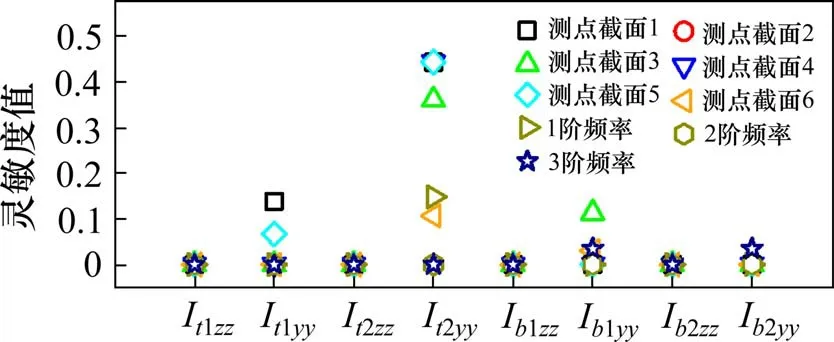
图10 局部模型各测点截面转角和频率灵敏度值Fig.10 Bending angle and frequency sensitivity values of each measuring point sectionin the local model

4.2 单独主梁横隔板处局部刚度修正

隔离单侧主梁进行单独研究，即将该主梁截面在桥塔处的节点自由度全部约束，形成一根端部固结的悬臂主梁，针对该单独主梁开展横隔板处局部刚度修正。此时，目标函数中静力项取为梁端截面转角残差，动力项取为主梁竖弯和横弯模态频率残差。寻优搜索计算时，ABC 算法中蜂群个体数SN为10，最大的迭代循环次数Cycle为300，最大保留次数limit为28，对应静转角残差的权重系数ω1和频率残差的权重系数ω2均取1。

修正后模型参数值见表4，修正前后主梁模型弹性模量E有约为0.56%的微小调整，这是由梁单元模型和实体单元模型之间的维度差异引起的微小误差；横隔板处主梁截面惯性矩Izz增长幅度最大，为48.41%，这是考虑横隔板刚度贡献导致的；横隔板处的截面惯性矩Iyy调整幅度次之，约为15.35%。从修正参数上的变化可看出，修正后主梁模型的刚度较初始模型都有不同幅度的提高，符合理论预期。

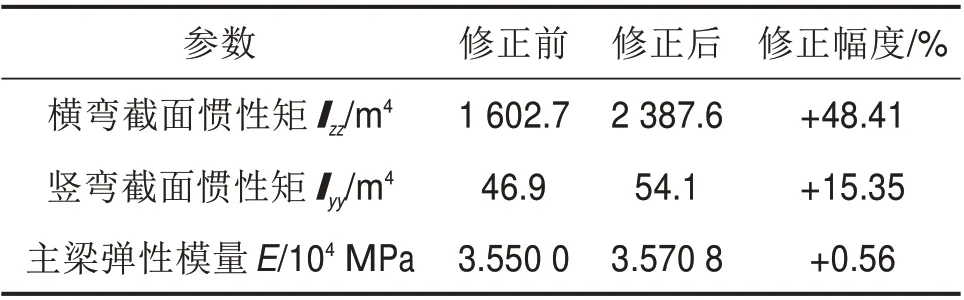
表4 单独主梁模型修正前后横隔板处单元参数对比Table 4 Comparison of element parameters at diaphragm plate before and after modification for single girder model

模型修正前后单独悬臂主梁的静动力计算结果见图11。修正后梁单元模型梁端截面转角值相对误差为0.18%，与实体模型结果几乎完全吻合；修正后梁单元模型1 阶竖弯和1 阶横弯模态频率相对误差均在0.01%以内，表明修正后梁单元模型更准确地反应其动力学性能，同时也表明人工蜂群算法在桥梁结构有限元模型修正中的有效性和实用性。

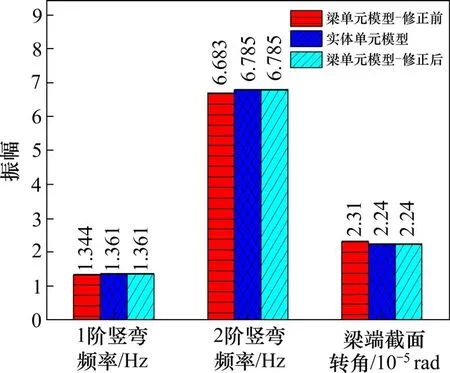
图11 修正前后的主梁结构静动力特性对比Fig.11 Comparison of static and dynamic characteristics of girder before and after modification

4.3 塔梁节点刚性区局部刚度修正

将上节所得主梁横隔板处最优参数代入梁单元塔梁局部模型，针对塔梁结合处节点刚性区进行局部刚度修正。此处目标函数中的静力项为5种荷载工况作用下(见图8)上塔柱−梁顶面交接处、下塔柱−梁底面交接处、左梁−塔交接处、右梁−塔交接处、梁端和塔顶共6 处测点截面(见图12)的转角残差。

图12 静力转角测点截面分布图Fig.12 Distribution of monitoring section for bending angle

目标函数中的动力项为前3 阶模态频率残差，分别为主梁1 阶竖弯、主梁1 阶横弯和主梁2 阶竖弯振型。寻优搜索计算时，ABC 算法中蜂群个体数SN为10，最大的迭代循环次数Cycle为450，最大保留次数limit 为38。对应静转角残差的权重系数ω1和频率残差的权重系数ω2均取1。

模型修正前后结构模态频率见图13，修正后梁单元模型的各阶频率相对误差均有所降低，以第3 阶模态频率最为明显，修正后第3 阶模态频率误差仅为−0.21%。图14 为梁单元模型修正前后节点刚性区截面转角对比，修正后5种荷载工况下节点刚性区截面转角值与实体单元截面转角值极为接近，修正后各荷载工况下节点刚性区截面转角值相对误差均在0.74%以下。图15 为修正前后塔顶和梁端截面转角对比，修正后各荷载工况下塔顶截面转角值相对误差较修正前均下降了3%左右，修正后各荷载工况下梁端截面转角值相对误差较修正前也均有所下降，下降幅度在1.73%～4.1%之间不等。这些结果表明，修正局部刚度后的梁单元模型能更准确地反映结构静动力特性，本文的修正方法是有效的。

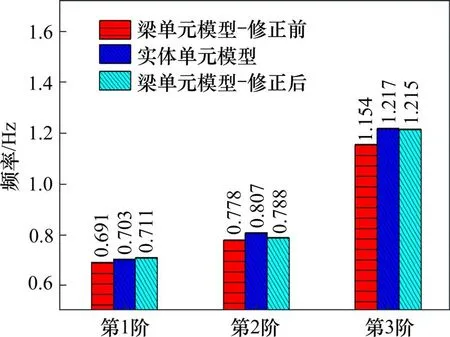
图13 局部塔梁模型修正前后模态频率对比Fig.13 Comparison of modal frequencies before and after modification of local tower beam model

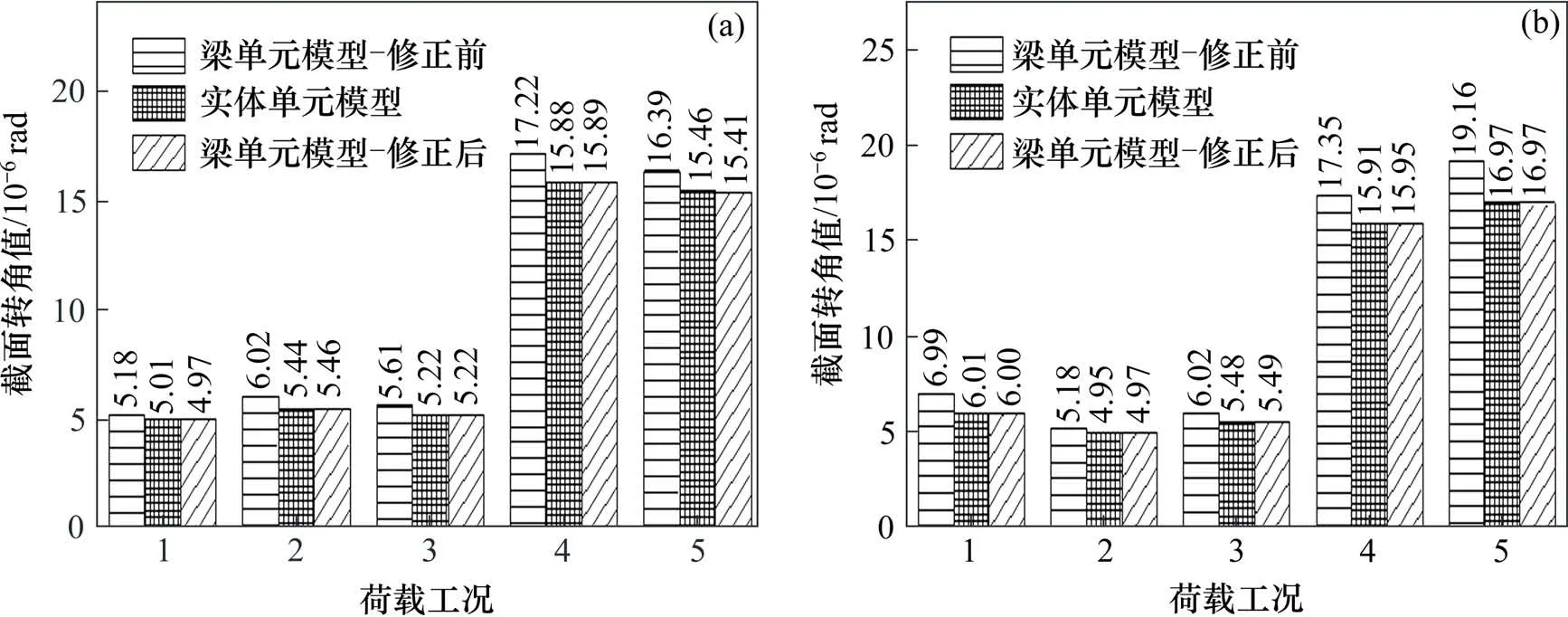
图14 局部塔梁模型修正前后节点刚性区截面转角对比Fig.14 Comparison of bending angle of nodal rigid zone before and after modification of local tower beam Model

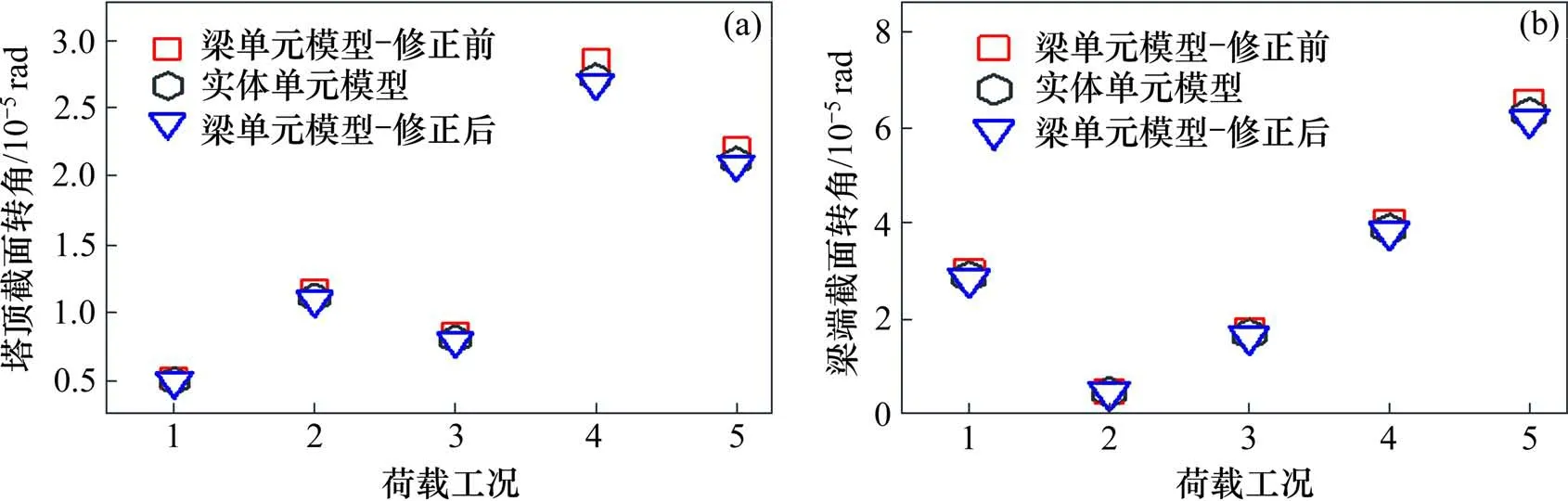
图15 局部塔梁模型修正前后静转角对比Fig.15 Comparison of static bending angle before and after modification of local tower beam model

梁单元模型修正前后参数对比见表5。修正前后塔梁结合处节点刚性区内的单元截面惯性矩It2yy，Ib2yy的变化幅度较小，分别为8.80%，43.16%；单元截面惯性矩It1yy，Ib1yy的变化幅度均较大，分别为70.35%，192.53%。表征单元局部刚度的参数积EIt1yy，EIt2yy，EIb1yy，EIb2yy增 长 倍 数 分 别 为1.70，1.09，2.93，1.43，呈现出在一定数值范围内的不等分布，说明节点刚性区内局部刚度的增强效应在不同区域上是不一致的，也从另一角度反映出单一提高弹性模量的传统刚性材料法建模方式的局限性。

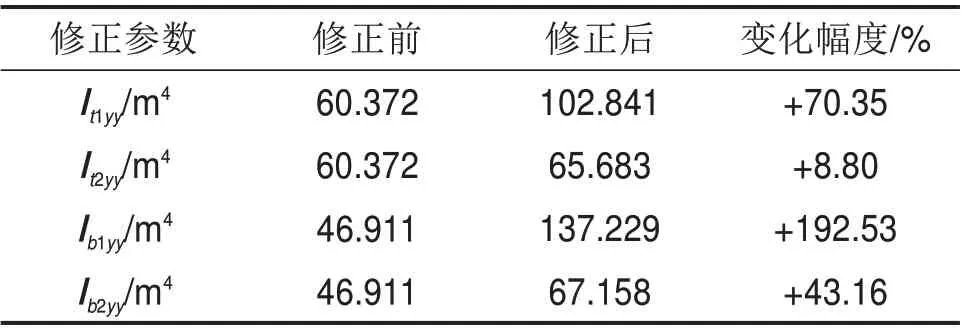
表5 修正前后节点刚性区内单元参数对比Table 5 Comparison of nodal rigid zone element parameters before and after correction

本文参数寻优过程使用的计算机硬件CPU 为AMD3900X，运行主频3.7 GHz，配备64 G 内存。对于单独主梁模型，其梁单元数量为17，优化计算搜索耗费计算机时间9.0 h，对于塔梁模型其梁单元数量为73，优化计算搜索耗费计算机时间12.75 h。相比于直接在实体元桥梁模型上开展动力响应计算时动辄数天甚至数周的时间花费，本文建议的优化方法可在继承梁单元桥梁模型动力分析效率的基础上，显著提高模型的计算准确度。

5 结论

1) 人工蜂群算法具备多变量系统参数寻优能力，适用于联合静动力学分析结果对桥梁结构有限元模型参数寻优修正。

2) 本文修正方法用于桥梁节点刚性区的局部刚度修正，可提高桥梁有限元模型的准确度，且修正过程客观，算例中修正后模型前3阶频率的相对误差分别下降至1.23%，−2.36%和−0.21%，节点刚性区各测点截面静转角值的相对误差均降到0.74%以内，更准确地反应结构静动力特性；

3) 修正后塔梁结合处节点刚性区内的刚度相比区外增加1.09～2.93倍，且在不同区域上的增强量不一致。

须说明的是，本文算例偏重于修正刚性区弯曲刚度以提高其准确度，实际工程建模时可进一步考虑修正扭转刚度以提高模型的扭转相关分析准确度；还可根据有限元模型的用途侧重，调整静−动参数残差权重系数之间的比例，针对性开展局部刚度优化，以期建立更准确反映静、动力学特征的梁单元模型。