地铁车辆段直线电机列车车致振动的试验研究

汪益敏，刘品言，陶子渝，陈皓粤，周杰

(1. 华南理工大学 土木与交通学院，广东 广州 510640；2. 广州地铁设计研究院股份有限公司，广东 广州 510010)

截至2019 年底，中国大陆共有40 个城市开通运营轨道交通线路208 条，总长6 736.2 km，其中地铁占比76.9%。地铁车辆段承担列车的运用管理、整备保养等任务，是地铁系统中占地最大的生产单位。与地铁配套的车辆段大量建设，加剧了城市用地紧张的局面。为了提高土地利用效率，车辆段的建设向空中和地下延伸，已有不少带上盖开发的车辆段投入运营[1−2]，列车运行产生的振动会影响上盖建筑的舒适度。地铁常用车型有A型车、B 型车和L 型车，其中L 型车为直线电机列车，其特点是车轮仅起支承和导向作用，不受黏着限制，这种牵引方式具有爬坡能力强、转弯半径小的特点，使选线更灵活，进而降低工程造价，适合在地形条件复杂、建筑物密集、轨道交通线网密布和地下空间资源紧张的城市中应用[3]。L 型车目前已应用于北京地铁首都机场线和广州地铁4，5 和6 号线。针对列车在车辆段运行引起的振动，谢伟平等[4]通过现场实测，研究了车辆段运用库列车振动荷载特性；冯青松等[5−6]基于现场实测，分析了列车运行引起试车线、咽喉区和检修线区域的振动特性差异，建立车辆段上盖建筑物有限元模型，分析了上盖建筑的振动特性；CAO 等[7−8]分析了高架车辆段和上盖建筑物楼板的振动；陈艳明等[9]测量了下沉式车辆段咽喉区钢轨、道床、地面、楼板及盖板的振动加速度；邹超等[10−11]分析了咽喉区地面、试车线临近建筑、车辆段上盖建筑的振动，研究了振动传播规律；汪益敏等[12]测量了试车线临近地面及建筑物的振动。以上研究，引起振动的列车主要是A 型车和B 型车，对于L型车产生的振动少有报道。本文采用JM3873 振动测试系统，对广州地铁6号线萝岗车辆段开展系列振动试验，研究车辆段上盖建筑振动响应规律，分析L型车振动特性。

1 试验方案

1.1 工程概况

广州地铁6 号线采用4 辆编组L 型车，长度为71.6 m，萝岗车辆段占地307 138 m2，盖下为检修库、停车列检库等车辆段建筑，总建筑面积130 767 m2，盖上主要用于物业开发(图1)。本次试验地点位于萝岗车辆段咽喉区和试车线附近，咽喉区轨道采用50 kg/m 钢轨、弹条Ⅰ型扣件、混凝土轨枕、碎石道床。试车线采用60 kg/m 钢轨、弹条Ⅲ型分开式扣件、梯形轨枕、碎石道床，铺设无缝线路。

图1 萝岗车辆段Fig.1 Luogang metro depot

1.2 测点布置

本次试验共设置3 个断面，断面A 位于咽喉区，该区域上盖建筑为钢筋混凝土框架结构，由于岩面起伏较大，基础采用冲孔灌注桩和独立基础2种形式，持力层为中风化花岗岩。在断面A 布置6 个测点(图2)，编号为A1～A6，测点A1，A3和A5 位于柱边，A2 和A4 位于框架梁跨中，A6 距1 号轨道中心线5.8 m，测点A1～A5 用于研究轨道正上方盖板振动特性，测点A6 用于研究L 型车在咽喉区运行时的振动特性。

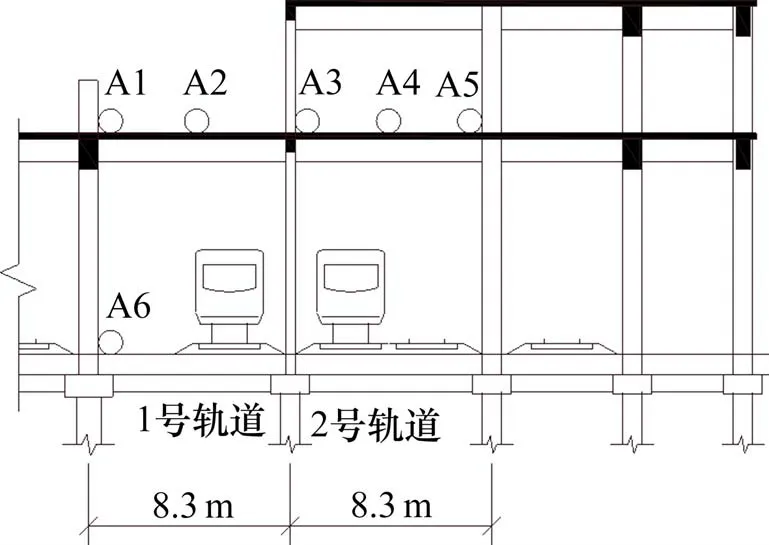
图2 断面A测点布置图Fig.2 Test points arrangement in cross-section A

断面B位于邻近咽喉区的后勤楼，测点布置如图3 所示，后勤楼共9 层，1，2 层为厨房及餐厅，3 层为停车库，4 至9 层主要是司机休息室。后勤楼为钢筋混凝土框架结构建筑，基础采用钻孔灌注桩和独立基础2种形式，桩端进入中风化或微风化花岗岩0.5～1 m，独立基础持力层为微风化花岗岩。场地特征周期为0.35 s。在后勤楼内每层布置一个测点，编号为B1～B9，测点B10 和B11 位于轨道和后勤楼之间的混凝土路面。

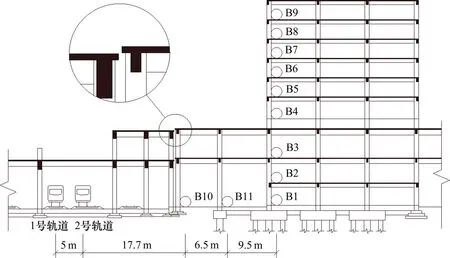
图3 断面B测点布置图Fig.3 Test points arrangement in cross-section B

断面C位于试车线一侧水泥混凝土路面，沿垂直轨道的方向布置6 个测点，编号为C1～C6，如图4 所示，其中C1 距轨道中心线7 m，用于研究L型车在试车线运行时的振动特性。

图4 断面C测点布置图Fig.4 Test points arrangement in cross-section C

L 型车通过试验断面时，记录上盖建筑和地面各测点的竖向和水平垂轨向振动加速度(下文水平向均指水平垂轨向)，采样频率为512 Hz。

1.3 舒适度评价指标

振动舒适度评价的常用指标是计权加速度级，该指标根据加速度时程数据计算。为了使离散数据的计算结果能真实反映连续振动过程，相邻2幅计算波形需要设置一定的重叠率，重叠率取3/4[13]。

根据《机械振动与冲击人体暴露于全身振动的评价 第1 部分：一般要求》(GB/T 13441.1 −2007)计算1～80 Hz对应的计权因子Wki，采用快速傅里叶变换处理每一秒的加速度时程数据，选取1～80 Hz 的频谱分量ai，按式(1)计算计权均方根加速度aw。振动计权加速度级VL按式(2)计算。

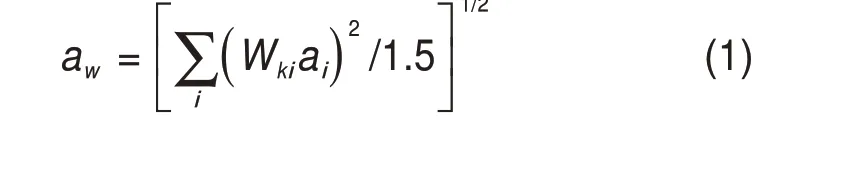
式中：aw为计权均方根加速度，m/s2；Wki为第i个频率对应的计权因子；ai为第i个频率对应的振动加速度均方根值，m/s2。

式中：VL为计权加速度级，dB；a0为基准加速度，10−6m/s2。

选取列车通过时计权加速度级最大值VLmax作为振动评价量。

2 试验结果与分析

2.1 断面A

共有15 列车通过断面A，其中有6 列车在1 号轨道运行，车速为11.6～13.8 km/h，另有8 列车在2号轨道运行，车速为10.9～13.5 km/h。测点A1～A5 的VLmax平均值如图5 所示。框架梁跨中的竖向振动大于柱边测点。对于水平向振动，框架梁跨中的振动小于柱边。盖板的竖向振动明显大于水平向振动。

图5 咽喉区盖板各测点振动加速度级Fig.5 Vibration acceleration level of each point on cover plate in throat area

分析临近轨道的地面测点A6 的振动实测数据，以了解L 型车的振动特性。图6 为列车以13.8 km/h 的速度通过1 号轨道时，测点A6 的竖向和水平向振动加速度时程，测点A6 竖向振动加速度峰值为0.462 m/s2，水平向振动加速度峰值为0.081 m/s2，该区域为直线轨道，L 型车引起的振动以竖向为主。根据振动加速度时程数据，计算振动计权加速度级，以确定L型车在咽喉区运行引起的振动量级。列车运行于1 号轨道时，测点A6 的竖向振动VLmax为85.8～87.4 dB，平均值为86.2 dB。

图6 测点A6振动加速度时程Fig.6 Vibration acceleration time signals of A6

采用快速傅里叶变换处理测点A6 的振动加速度时程数据，窗函数选用汉宁窗，按幅值相等的原则进行修正，图7为上述振动加速度时程对应的频谱。测点A6 的竖向振动响应频带为30～150 Hz，频谱峰值所在频率为70 Hz。其余5 列车通过1 号轨道时，测点A6 的竖向振动频谱峰值所在频率为63～70 Hz，次峰值所在频率为32～33.5 Hz。

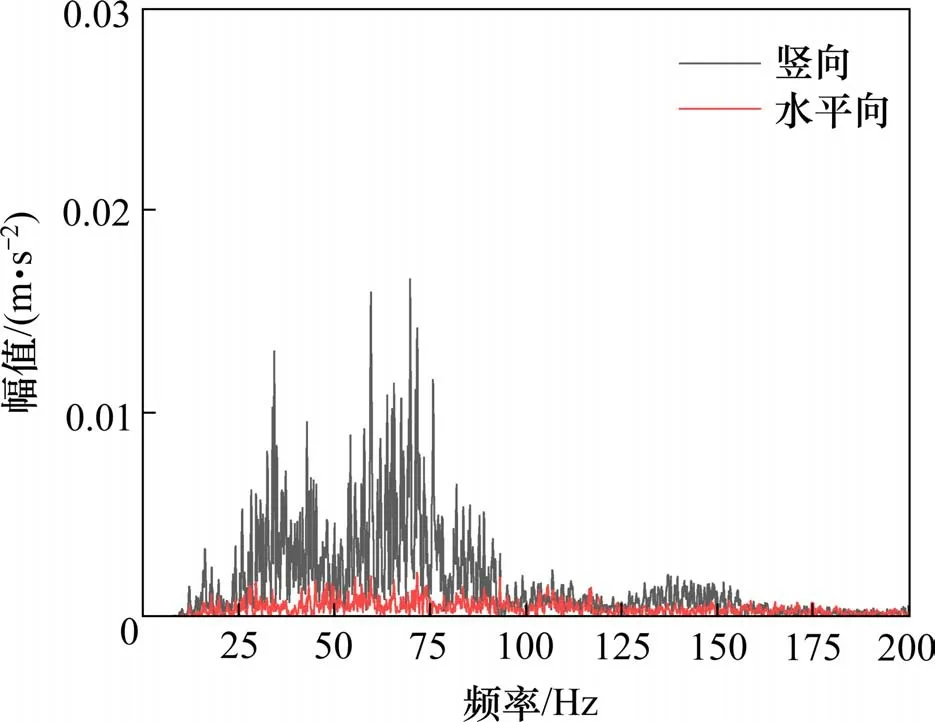
图7 测点A6振动加速度频谱Fig.7 Vibration acceleration frequency spectra of A6

2.2 断面B

测得的11 组有效数据中，有4列车在1 号轨道运行，车速为12.8～13.5 km/h，另有7 列车在2 号轨道运行，车速为11.1～12.2 km/h。测点B1～B9的VLmax平均值见图8。对于竖向振动，随楼层增高，楼板的振动强度呈波浪形变化[14]，竖向振动最大的位置为4 层楼面，若仅在建筑物1 楼室内布置测点，无法反映建筑内振动的最不利情况。水平向振动最大的位置是3层楼面。后勤楼内，各测点的VLmax均小于60 dB，满足舒适度要求，已有研究表明，桩基础对振动的削弱效果较好[15]。

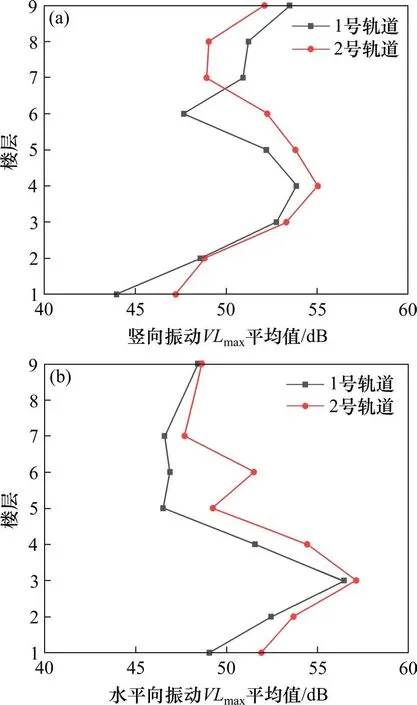
图8 后勤楼各测点振动加速度级Fig.8 Vibration acceleration level of each point in logistics building

结构的振动响应除了受列车运行影响，主要由结构的质量分布和刚度分布决定。对于竖向振动，取测点所在的柱及半跨楼板作为计算单元，各层柱截面尺寸均为800 mm×800 mm，按式(3)计算各层柱竖向刚度，结果见表1。

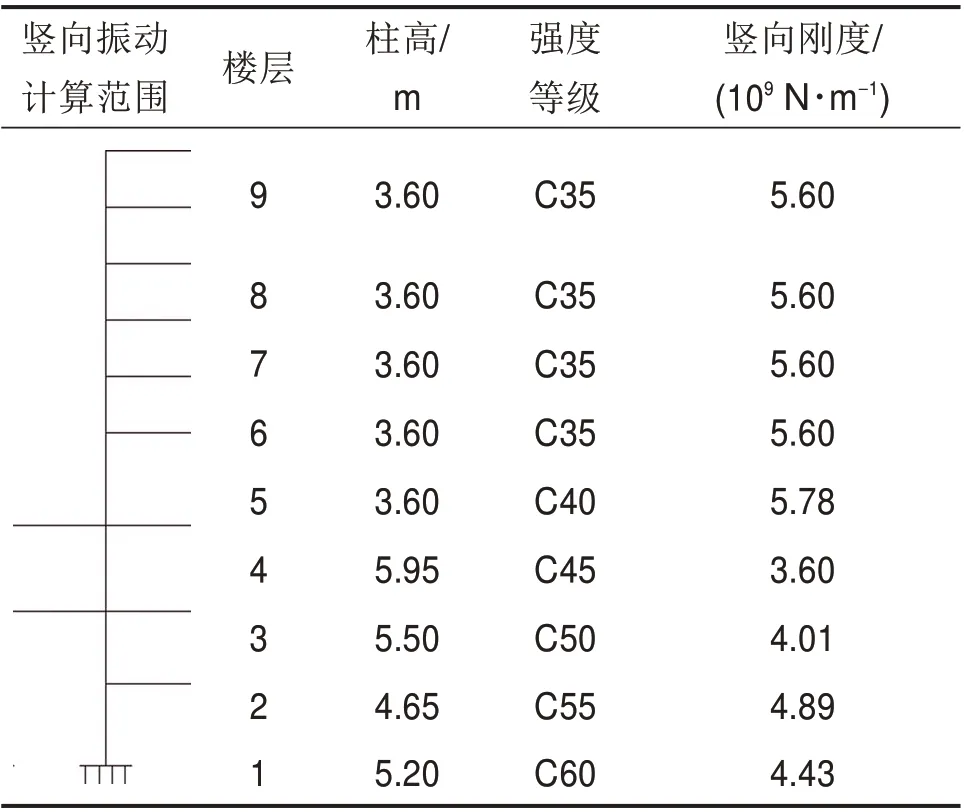
表1 后勤楼振动分析参数Table 1 Parameters of logistics building vibration analyses

式中：Kc为各层柱竖向刚度，N/m；Ec为混凝土弹性模量，N/m2；Ac为柱截面积，m2；h为柱高，m。

根据各层竖向刚度，得到刚度矩阵KZ。将质量集中在每一层楼面处，从2层楼面到屋顶依次编为质点1～9，忽略活载，各质点的质量mi依次为35.68， 58.85， 118.78， 38.63， 36.71， 36.71，36.71，36.71 和46 t，得到质量矩阵MZ。将列车运行引起的振动近似按地震考虑，采用振型分解反应谱法，计算各质点所受的竖向地震作用。忽略阻尼，下式为该体系的自由振动方程：

式中：ω为自振圆频率，rad/s；Z为各质点位移幅值，Z={Z1,Z2,…,Z9}T。

仅考虑第1振型，由|KZ-ω2MZ|= 0，得到ω1=53.24 rad/s，T1=0.12 s。将第1 自振圆频率ω1=53.24 rad/s代入式(4)，同时令Z9=1，得到体系自由振动第1 振型各质点的相对位移：Z1i={0.19, 0.36,0.55,0.71,0.80,0.88,0.94,0.98,1}T。第1 振型的振型参与系数按式(5)计算，得到γ1=1.30。

各质点所受竖向地震作用按式(6)计算，得到F1i={0.87, 2.71, 8.37, 3.52, 3.75, 4.10, 4.38, 4.57,5.87}T×105×αv,max。

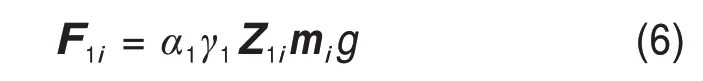
式中：α1为相应于第1 振型自振周期T1的地震影响系数，设为αv,max；g为重力加速度，9.8 m/s2。

假定每个质点所受竖向地震作用仅对本层柱的变形产生影响，对其他各层柱变形的影响可忽略不计。用各质点所受竖向地震作用除以各层柱竖向刚度，得到各质点的竖向位移：zi={1.97,5.54,20.86,9.77,6.49,7.33,7.82,8.17,10.47}T×10-5×αv,max。将所得结果除以1.97×10−5×αv,max，得到后勤楼振动相对位移，结果见图9。

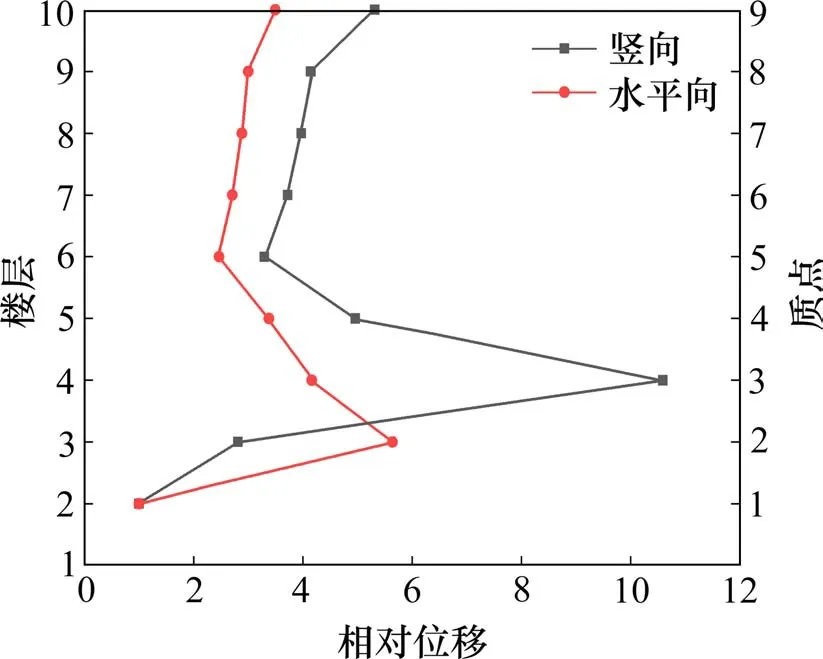
图9 后勤楼振动相对位移Fig.9 Relative displacement of vibration in logistics building

竖向位移最大的位置出现在4层楼面，该楼面回填有1.8 m 厚的泡沫混凝土(重度约4.5 kN/m3)，导致4层楼面的质量明显大于其他各层，对结构振动产生了不利影响。

对于水平向振动，同一楼层近似按整体振动考虑，取测点所在的平面框架进行分析，计算单元宽度取相邻跨中线之间的距离。根据梁柱线刚度计算框架各层的侧向刚度(D值)。同样采用振型分解反应谱法，计算各质点相对位移，结果见图9。

侧向位移最大的位置是3层楼面，由于部分柱从基础顶面到3层楼面未与框架梁连接，导致该层对应的侧向刚度较小。由上述分析可见，竖向和水平向振动均显著受刚度分布和质量分布影响，通过分析结构振动特性，可以大致确定振动最大的楼层。

2.3 断面C

试车线轨道结构不同于咽喉区，列车在试车线运行时速度较快，振动特性有所不同。根据测点C1 实测数据，分析L 型车在试车线运行时环境振动特性。

在该区域共测得11 组有效数据，车速为10.2～22.2 km/h。图10 为列车以20.5 km/h 的速度通过断面C 时，测点C1 的振动加速度时程，竖向振动加速度峰值为0.833 m/s2，水平向振动加速度峰值为0.131 m/s2，竖向振动明显大于水平向振动。根据测得的11 组振动加速度时程，计算竖向振动计权加速度级，得到测点C1 的竖向振动VLmax为87.9～93.3 dB，平均值为91.7 dB。

图10 测点C1振动加速度时程Fig.10 Vibration acceleration time signals of C1

图11 为上述振动加速度时程对应的振动频谱，竖向振动峰值频率为53 Hz。其余10组数据竖向振动频谱峰值所在频率为50～54 Hz，振动响应频带为30～100 Hz。

图11 测点C1振动加速度频谱Fig.11 Vibration acceleration frequency spectra of C1

3 讨论

马龙祥等[16-17]研究了A 型车和B 型车在隧道运行时环境振动的差异，认为A 型车的环境振动影响更大。林楚娟等[18]选择2 个带上盖的车辆段，实测了A型车和B型车在试车线运行时，轨道临近地面的振动，距轨道中心线3～30 m 的范围，A 型车引起的竖向振动约为60～75 dB；距轨道中心线2.5～30 m 的范围，B 型车引起的竖向振动约为55～79 dB。汪益敏等[12]在厦滘车辆段进行了现场实测，得出B 型车在试车线运行时，距轨道6～28 m 的范围，竖向振动为76.2～91.2 dB，距轨道6 m 的测点竖向振动响应频带为10～120 Hz，峰值频率约为40 Hz。本试验断面C 的结果表明，L 型车在试车线运行时，距轨道中心线7～30 m 范围内引起的竖向振动平均为65.1～91.7 dB，与B 型车引起的振动量级相当，振动的低频成分少于B型车。

对于列车在车辆段咽喉区运行时的振动特性，陈艳明等[9]测量了A 型车在下沉式车辆段咽喉区运行时，钢轨和道床的振动，得出道床的振动主频段为80～200 Hz。何卫等[19]测量了B型车在咽喉区运行时轨枕的铅垂向振动，得出轨枕振动主频段为60～150 Hz。相比较而言，L型车在咽喉区诱发的振动主频段在30～45 Hz 和60～75 Hz 2 个区间(图7)。

地铁车辆运行诱发的环境振动与轨道结构、车速以及场地条件有关，不同类型地铁车辆的环境振动特性比较和分析，还有待进一步研究。

4 结论

1) 根据咽喉区盖板的振动试验结果，同一楼层中，对于竖向振动，框架梁跨中的振动大于柱边，对于水平向振动，柱边的振动大于跨中。

2) 对于不同楼层的振动，振动计权加速度级的大小受结构质量分布和刚度分布的影响，竖向振动较大的位置出现在重量大的楼层和顶层，水平向振动最大的位置是侧向刚度较小，而重量较大的楼层。通过分析结构振动特性，可以大致确定振动最大的楼层，建议选择振动舒适度评价的测点时，根据结构的具体情况确定。

3)L型车在咽喉区直线轨道运行时，距轨道中心线5.8 m 的地面，振动加速度级可达87.4 dB，振动响应频带为30～150 Hz。

4)L 型车在试车线运行时，距轨道中心线7 m的地面，振动加速度级可达93.3 dB，振动响应频带为30～100 Hz。