考虑施工动态影响的施工期管片上浮分析

胡 勇

(中铁十八局集团有限公司 天津 300222)

1 引言

近年来盾构法应用越来越广泛，尤其是在过江隧道和城市地铁中。但是盾构隧道也出现了很多问题，施工阶段管片脱离盾尾后，容易出现上浮现象[1－3]，可能会引起管片错台与破损、环间螺栓剪断，渗漏水等安全事故的发生，严重影响隧道成型质量。因此为保证隧道施工与运营的安全，有必要对管片施工期的上浮规律进行研究，及时采取科学合理的应对性措施。

国内外很多学者对盾构隧道施工阶段产生的上浮现象进行了研究。舒瑶等[4]通过现场试验分析得到同步注浆是管片上浮的重要因素。数值模拟和现场实测在一定程度上可以对施工进行指导，但是不能深入揭示管片上浮的机理。因此对管片的上浮进行理论分析尤为重要。国内外很多学者对盾构隧道施工期的管片上浮机理进行了研究，且已经取得了一定的成果。朱令等[5]基于等效纵向上浮分析模型，考虑动静态上浮力、浆液特性等的影响下建立了盾构隧道纵向上浮分析模型。王道远等[6]基于温克尔无限长梁微分方程推导出盾构隧道纵向上浮的理论解。Talmon[7]、王道远等[8]对等效连续梁模型进行改进，建立了盾构隧道纵向上浮分析模型预测管片上浮量。目前的理论分析模型大多没有考虑施工动态的影响，将管片上浮视为静态过程进行分析。实际上随着盾构隧道不断向前掘进，由于管片之间通过螺栓进行连接，因此后面施工的管片通过螺栓力的传递会导致先前施工的管片继续上浮，管片的上浮实则为动态累加的过程。

针对上述不足，本文在前人[9－11]基础上，基于弹性地基上的温克尔半无限长梁理论和等效连续梁理论，建立纵向隧道上浮分析模型。该模型考虑施工动态的影响，可以模拟盾构隧道动态施工过程，进而得到纵向上浮量的分布。最后将得到的计算结果与实际工程监测数据进行对比，验证了模型的合理性。

2 隧道上浮分析

同步注浆是引起隧道上浮的重要因素，当管片脱离盾尾后，在同步注浆的作用下，盾构隧道会持续地产生上浮。在此过程中，隧道主要受到3种载荷的作用，自重、动态上浮力和静态上浮力。

自重根据定义可以表示为:

式中，ρ为管片的密度；V为管片的体积。

由同步注浆引起的上浮力也称动态上浮力，假设动态上浮力在环向为扇形分布，则上浮力的计算式为:

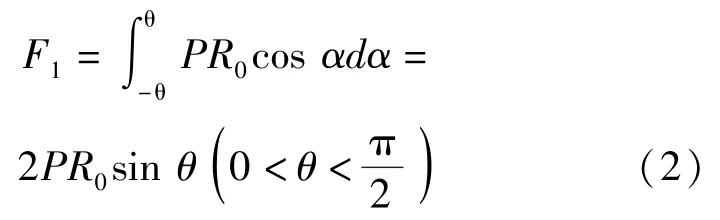
该公式一般适用于压密注浆，式中θ为扇形区域的边界和竖直方向的夹角，P为注浆压力。当θ＝45°为最不利的情况，此时得到的动态上浮力最大。动态上浮力其大小、分布形式与注浆工艺密切相关。

由地下水、注浆浆液、泥浆等包裹管片而引起的上浮力为静态上浮力，可表示为:

式中，R0为管片外径；γi为浆液容重。

3 弹性地基梁模型

本文基于弹性地基梁和等效连续梁建立施工期管片上浮分析模型，把隧道看作是弹性地基上的半无限长等效连续梁，以盾构机尾部作为半无限长梁的自由端。盾尾内一般预留有2～3环管片。当管片脱出盾尾时，除了受同步注浆产生的上浮力外，考虑到节间抗浮效应的影响，盾尾内管片还对上浮管片产生向下的抗浮力。分别求解上浮力、抗浮力单独作用于半无限长梁的解析解，然后再运用叠加原理即可求得。

目前无限长梁自由端受集中荷载已有很成熟的解析解，其任意截面处的挠度曲线可表示为:

式中，P为集中荷载；K为地基反力系数；λ为无限长梁特征系数，与等效梁刚度和地基反力系数有关。

半无限长梁受分布荷载作用时，不能直接求出其解析解。可以把分布荷载看成无数个集中荷载，同时把半无限长梁转化为无限长梁进行求解。如图1所示。

图1 无限长梁转化为半无限长梁

从图1可知，分布荷载在无限长梁的原点处会产生一个弯矩M(0)和剪力Q(0)，而事实上半无限长梁的自由端不存在弯矩和剪力。因而在自由端施加一个大小相等、方向相反的弯矩M′和剪力Q′，就可得到分布荷载作用下半无限长梁的挠度方程:

盾构施工为一个动态过程，盾构机每向前掘进一环，则相应的荷载向前移动一环，半无限长梁的自由端也向前移动一环，如此恰好模拟了盾构施工的动态过程。施工步示意如图2所示。

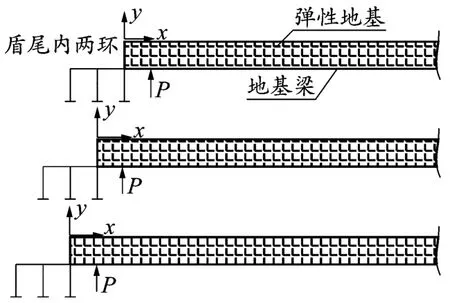
图2 施工动态简图

考虑施工步的影响时，管片的上浮是一个累加的过程。如1号管片脱离盾尾后，在上浮力的作用下产生上浮量w1。此时认为管片下面的浆液固结产生一定的强度支撑管片，使其不会下沉。随后2号管片脱出盾尾，在新的上浮力作用下1号管片产生新的上浮量w2。以此类推，当n号管片脱出盾尾时，1号管片的上浮量为wn。很显然当n足够大时，wn会趋向0，此后1号管片不会产生新的上浮量。因此1号管片最终的上浮量为:

4 工程实例分析

本文以祈福站～番祈中间风井盾构区间段典型断面作为工程算例，该截面对应的管片为2 079环。注浆口浆液压力控制在0.18 MPa左右，地层剖面图如图3所示。

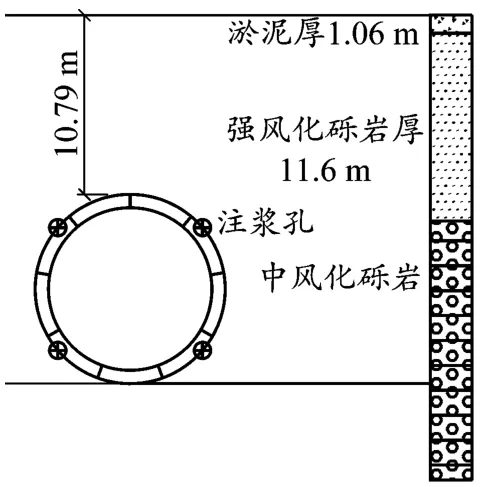
图3 典型断面地层剖面图

计算所需的参数如表1所示。

表1 浆液和地层参数

假设隧道截面完全均质，参考叶飞等[12]的刚度计算方法可得到纵向等效刚度为(EI)eq＝9.08×108 kN·m2。基于温克尔半无限长弹性地基梁模型，可以得出隧道上浮量预测如图4所示。

图4 管片上浮理论值

从图4可以看出，刚脱出盾尾的管片上浮量最大，约为2.2 mm。随着地基梁离盾尾的距离增大，上浮量逐渐变小，约45 m处变为0。随之约45～60 m出现负位移，数值很小，最大约为0.1 mm。当距离盾尾超出60 m，管片上浮量一直保持为0。

实际施工时盾构机不断向前掘进，还应该考虑施工步的影响，第1环管片刚脱出盾尾后上浮2.2 mm。而后盾构机往前掘进，新的管片脱出盾尾。由于该环管片还处于同步注浆的影响范围内，所以会继续产生上浮，如第5环管片脱出盾尾时第一环仍继续上浮1.6 mm，10号管片脱出盾尾时目标环管片仍继续上浮0.8 mm。当盾构机往前掘进约30环时，即第30环管片脱出盾尾时，目标环管片不再继续上浮。管片的上浮量随施工步的增加而增加，当超出一定施工步，上浮量不再发生变化。

为了和现场实测数据进行对比，把各个施工步下第1环管片的上浮量进行叠加，可以得出该环管片随施工步变化的动态过程，如图5所示。

图5 目标环管片上浮量理论值

从图5可以看出第1环管片的上浮量不断增加，但增加的速率变小，最终在管片离盾构机为约60 m时，上浮量不再增加，最终的上浮量在28.0 mm左右。图5还给出了现场的监测数据，原始的监测数据是按天数记录的，现在为了跟弹性地基梁的理论值进行对比，将其转化为第一环脱出盾尾后离盾尾的距离值。现场的施工数据表明每天盾构隧道掘进3～4环，取平均值3.5环(7 m)。因此，当第一环管片脱出盾尾后，选取15 d的监测数据进行绘图，发现第一天上浮量增加较快，上浮量达到15 mm。随后上浮量继续增加，但上浮速率减慢，10 d以后保持不变，最终上浮量稳定在28.7 mm。

5 结论

本文基于弹性地基梁模型和等效连续梁模型，建立了半无限长弹性地基梁模型，并且对施工期管片上浮量进行预测，与现场监测数据进行了对比，得出以下结论:

(1)刚脱出盾尾的管片上浮量最大，距离盾尾越远的管片上浮量越小，约45 m处变为0。随之出现一小段负位移。当管片距离盾尾超出60 m时，管片上浮量一直保持为0。

(2)考虑施工步影响时，目标环的上浮量逐渐增大，但上浮速率变小，之后目标环距离盾尾60 m处时，目标环的上浮量不再增加。模型理论值和现场实测数据较为吻合，说明本文方法在计算管片上浮方面具有独特的适用性和有效性。