互联网思维下的小学数学概念教学——以“分数”的教学为例
张 晶
随着互联网的兴起和广泛应用,互联网思维也渐渐走进人们的生活,越来越得到人们的重视。互联网思维是指人们立足于互联网去思考和解决问题的思维,其内核是用户思维、去中心化思维以及简约思维。小学生的数学学习过程,其实就是不断建立数学概念的过程。如何让数学概念教学更生动有效?笔者认为,教师可以立足用户思维,切实处理好“课堂教学中谁为中心”的问题,努力让数学课堂散发其特有的简约思维的魅力,促进学生深度理解与运用数学概念。
一、用户思维下的小学数学概念教学
借鉴互联网的“WHO—WHAT—HOW”模式,在数学概念教学中,教师需厘清三个问题:用户是谁?用户需要什么?应以怎样的方式来满足用户的需求?
1.定位对象:把握概念教学的起点。
学生是教育教学的对象,是发展需求的发出者,也是教育教学活动的主体,还完全可以成为创造者。如教学苏教版三上《分数的初步认识(一)》一课,磨课时,大家不约而同想到一个问题:学生对分数究竟了解多少?对学习影响最大的因素是学习者关于自己将要涉足的知识领域的先有认知。学生之前虽有一些关于分数的知识储备,但分数的概念对他们而言不仅抽象而且难理解。教师需要以关心用户的姿态,深入了解学生的学习起点,进而思考和设计相应的教学活动。
2.规划思路:聚焦概念认知的节点。
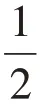
3.体验至上:创设深度参与的概念学习活动。
从产品体验来看,互联网是典型的体验经济。简言之,就是“让用户参与进来,建立一个可触碰、可拥有,和用户共同成长的品牌”。同样,概念教学很重要的一点就是要围绕“如何深化学生对概念的‘体验’”展开,教师需要结合教学目标组织学生开展高质量的学习活动。如教学《分数的初步认识(一)》一课,教师设计了以下学习活动。
【体验活动】
师(出示图1):篮子里有2杯饮料和1个比萨,每人选一样,折一折、分一分,自己尝试用这样的句子,说一说分的过程和结果。
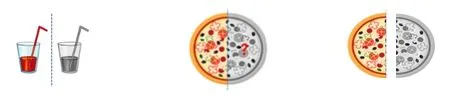
(图1)
课件出示:把2杯饮料平均分成2份,每人分得( )杯;把1个比萨平均分成2份,每人分得( )个。有困难的同学,可以向同伴求助。
【分享成果】
(1)分一分:分完了饮料,还有1个比萨,你要怎样把它平均分成2份呢?一边折一边说。
(2)说一说:怎么分?“对折”好在哪里?加一条虚线表示平均分成2份,哪部分是半块?
(3)想一想:你取了左边的一份,如果换成取右边的一份,可以吗?为什么?
(4)思一思:回顾刚才平均分饮料和比萨的过程,有什么不同点和相同点?还有什么疑问?
(5)悟一悟:不同点在于总数和结果;相同点在于分和取的过程。

二、去中心化思维下的小学数学概念教学
互联网思维的去中心化是指网状结构的互联网不是一个层级结构,没有中心节点,且不同的点有不同的权重。去中心化的课堂没有绝对的权威,谁都不是唯一的中心。基于此,就需要我们从教师主导的退隐、核心问题的贯穿以及对话场域的构建等方面着手开展数学概念教学。
1.教师主导的退隐:让出概念学习的时空。
众所周知,课堂中教师的主导作用难以替代。但在去中心化思维下的小学数学概念教学中,教师主导的退隐意在让出概念学习的时空,给予学生更多机会去探索,让学生真正成为概念学习的主体。从上述案例中可以看出,教师适时调整自己在课堂中的站位,看似退让的背后,是学生在认识分数过程中的主动进取,是在激发学生分、想、思、说、悟等的过程中让其思维清晰可见的一种教学智慧。
2.核心问题的贯穿:保持概念学习的动力。
美国数学家哈尔莫斯说:“问题是数学的心脏。”有价值的核心问题是一节课的灵魂。教师应努力让学生时刻关注核心问题,从而使他们持久保持学习的动力,逐步将其思维引向深处。如教学《分数的初步认识(一)》一课,在“自主创造,引出分数”环节,教师抛出核心问题:每人分到1杯饮料,可以用数字1表示,半个披萨该用怎样的数来表示呢?你能想办法自己“发明”一个数吗?这是教师提炼出的贯穿全课的核心问题。好问题能引发数学思考。学生自然联系前面的体验活动展开想象和思考。核心问题搅动了学生的思维,有些学生的思维表达(如图2)已经逼近分数的本质了。

(图2)
3.对话场域的构建:共享概念学习的成果。
互联网离散的、去中心化的结构模式决定了“网络面前人人平等”。将平等性的特点迁移到课堂教学中,即强调师生间平等对话和交流。平等对话场域的积极构建使得教学中心得以灵活转变,不同的学生被关注,进而被认可,推动个性化和差异化教学的实施,促进学生共享学习成果。如教学《分数的初步认识(一)》一课,教师投屏出示不同学生的学习成果(如上图2),并提问:这些图表示什么意思?学生解释后,教师问大家:他们的解释你听懂了吗?这里的“2”和“1”分别表示什么?学生发言之后,教师继续启发学生思考:他们的作品有什么相同之处?概念是抽象的,活动是开放的,思维是活跃的。在这个对话场域中,每个学生都有机会创造并表达自己对分数独特的见解与思考。
三、简约思维下的小学数学概念教学
简约思维运用到互联网时代的经济领域有两个原则:一是专注,少即是多;二是大道至简,简约即美。数学概念的学习过程本身就是用简约、抽象的科学方式来表达去伪存真、删繁就简的思考、创造与发现的过程。
1.板块简约:促发概念学习的整体性。
数学知识具有结构化和整体性的特点。课时教学可以从整体出发,精准设计情境、活动、练习等,让教学层次更清楚,让教学重点更突出。如一位教师执教苏教版三下《求一个数的几分之一是多少》一课时,设计了两个探究活动。
探究活动一:出示图3,让学生自主探索总数相同的几分之一(不同)是多少。可以分一分、涂一涂、算一算。
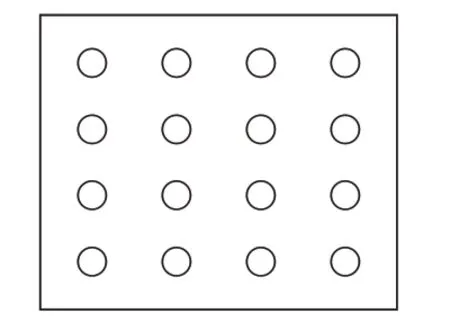
(图3)
探究活动二:出示图4,让学生感受总数不同的整体的几分之一(相同)是多少。
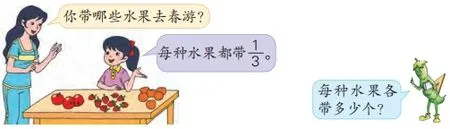
(图4)
教师优化知识内容的呈现方式,通过两个简约的板块深入浅出地展开“整体的几分之一是多少”的教学,既凸显了知识的结构化和整体性,也诠释了“少即是多”的内涵。
2.问题简约:凸显概念学习的本质。
抽象的概念需要简约的表达。教师教学概念时要把握“以问题为中心,凸显数学本质”的原则,推进简约教学的有效实施。如教学《求一个数的几分之一是多少》一课,教师设计了如上页图3所示的开放题。在分享交流环节,教师惊喜地看到学生的思维真实、清晰而深刻地呈现了出来。
生:就是把16个○平均分成2份,求每份是多少,所以用16÷2。
师:那16÷16=1(个),你能解释这个算式中的两个16分别表示什么吗?
生:我知道!第一个16表示总共有16个○,第二个16表示平均分成16份。
师:你的思维真清晰,太棒了!
问题精简更利于聚焦重点,有助于引导学生走近概念,用数学思维去思考问题,更快地触摸到概念的本质。
3.思维简约:通向概念学习的抽象性。
德国哲学家康德说:“人类的一切知识都是从直观开始,从那里进到概念,而以理念结束。”基于此,有必要在概念教学中通过思维的简约让学生习得数学的抽象性。如教学《求一个数的几分之一是多少》一课时,教师抛出如上页图3所示的问题,答案显然不唯一,学生逐渐发现不同的答案之间有着密切的联系。他们的思维渐渐触及分数的本质——平均分。在充满浓郁“数学味”的活动中,学生隐隐感悟到隐藏在其背后的神秘的“总数1”,再通过两次“变与不变”的对比,从不同的视角理解分数的意义,慢慢体悟并抽象出“求一个数的几分之一是多少”的方法。数学抽象是数学求简性的重要表现。教师要帮助学生清楚地认识超越直接经验的重要性,不断提高其思维的精确度与简约度。
综上所述,在互联网时代,小学数学概念教学模式的研究呈现出多元化和现代化的特点。教师需要学习和探索互联网思维的精髓,打破固化的教与学方式,不断优化教学,聚焦学生思维品质的培养,以有效的教学策略引领学生从形象思维向抽象思维不断进阶,引导学生爱上思考、爱上数学。

