发动机控制系统限时派遣运行的成本优化方法

韩冰，陆中，张子文，易阳，李超

南京航空航天大学 民航学院，南京 211106

限时派遣(Time-Limited Dispatch, TLD)分析指机载系统的冗余单元故障后，在满足安全性要求的条件下，不需要立即维修，允许系统带故障派遣一段规定长度的时间。飞机运营商可将维修计划安排在该时间间隔内的任意时刻，以避免由于故障立即维修而导致航班延误或取消，从而提高飞机的签派可靠度[1]。TLD分析是商用飞机及航空发动机系统安全性分析的重要组成部分，是针对25.1309“设备、系统及安装”、33.28“发动机控制系统”以及CS-E1030“限时派遣”等适航条款进行符合性验证的重要内容，已经成为安装FADEC系统的商用航空发动机以及安装此类发动机的商用飞机开展型号合格审定、获取型号合格证必须进行的一项符合性验证工作[2-4]。

目前开展的TLD分析普遍将安全性要求视为唯一的约束条件，即在满足平均完整性要求以及故障出现后的瞬时安全性要求的前提下，确定系统允许带故障派遣的时间间隔。文献[5-6]以系统平均完整性水平为要求，基于马尔可夫模型法，建立了系统带单故障派遣的时间间隔与平均完整性水平的函数模型。文献[7]对基于马尔可夫模型的带单故障派遣的平均完整性水平建模方法的精度误差来源及影响进行了分析与验证。文献[8-9]对文献[5-6]的方法进行了改进，利用马尔可夫模型法，建立了系统带双重故障派遣的时间间隔与平均完整性水平的函数模型。文献[10-13]应用蒙特卡罗仿真方法，建立了带故障派遣的时间间隔与平均完整性水平的函数模型。文献[14] 提出了冗余系统带多重故障运行的派遣类别决策方法，针对典型全权限数字式发动机电子控制(Full Authority Digital Electronic Control, FADEC)系统，提出了系统带多重故障派遣的时间间隔决策方法。文献[15]考虑了维修策略对TLD分析的影响，提出了基于蒙特卡罗仿真法的全修复策略下FADEC系统带多重故障派遣的时间间隔决策方法。

将平均完整性水平视为唯一的约束条件，只能满足安全性要求。实际上，飞机运营中不可派遣(Non-Dispatch, ND)状态会经常出现，由于该状态的发生概率与飞机延误、取消率密切相关，若只满足安全性要求，而不考虑签派可靠度的约束，将会使飞机的签派可靠度降低。文献[16-17]考虑了TLD分析中的ND状态，将系统平均完整性水平与签派可靠度均作为设计要求，提出了带故障派遣时间间隔决策方法，从而保证飞机能够满足安全性要求的同时也能将延误率和取消率降低到可接受的范围之内。

从上述文献可以看出，目前的TLD分析方法仅考虑了安全性与可靠性约束，未考虑带故障派遣时间对飞机运行成本的影响，不能实现安全性与经济性的综合优化。本文以飞机运行成本优化为目标，对航空发动机控制系统开展了限时派遣分析方法研究。面向TLD分析建立了包含ND状态的典型发动机控制系统马尔可夫模型，利用连续时间马尔可夫链(Continuous Time Markov Chain, CTMC)推导了状态稳态频率公式，构建了系统单位时间运行成本模型,以平均完整性要求及签派可靠度要求为约束条件，以带故障派遣时间为决策变量，以系统单位时间运行成本以及签派可靠度为优化目标，分别构建了TLD分析的单目标与多目标优化模型。应用本文方法进行带故障派遣时，能够保证飞机在满足安全性要求和签派可靠度要求的条件下降低运行成本。

1 TLD分析的基本概念

根据故障发生后的瞬时LOTC率，可将系统带故障运行状态分为3类，分别是ND状态、短时派遣(Short Time, ST)状态以及长时派遣(Long Time, LT)状态[1]：

1) ND状态：若瞬时LOTC率大于1×10-4时，则不允许带故障派遣，故障必须立即修复。

2) ST状态：若瞬时LOTC率在区间[7.5×10-5,1×10-4) h-1内，可带故障派遣较短的时间间隔TST，故障必须在时间区间[0,TST]内修复。

3) LT状态：当瞬时LOTC率在区间[1×10-5,7.5×10-5) h-1内时，可带故障派遣较长的时间间隔TLT(TLT>TST)，故障必须在时间区间[0,TLT]内修复。

TLD分析的目的是发动机控制系统在满足平均完整性水平小于或等于1×10-5h-1的条件下，确定短时派遣时间TST及长时派遣时间TLT。

2 单位时间运行成本建模

2.1 TLD分析的马尔可夫模型构建

在利用马尔可夫模型进行TLD分析时，模型中除了包含ND、ST与LT状态外，还包括无任何故障的完好(Full-up, FU)状态以及LOTC状态。

一般情况下导致系统发生LOTC事件的故障原因分为3类：双余度的电子电气部件均发生故障、液压机械组件(Hydro Mechanical Unit, HMU)故障以及未覆盖的电子电气部件(Uncovered, UC)故障。UC故障是指无法检测或容错的每一控制通道的电子电气故障，由于这些故障无法容错，因此其将导致LOTC事件[1]。LOTC事件一旦发生，系统推力控制丧失，需要立即修复。

ND状态的发生，将极大地降低系统的安全裕度，因此也必须立即修复。通常发动机控制系统构型中的所有电子电气部件均具有冗余，单个部件故障一般不会导致ND状态。导致ND状态的主要原因是电子电气部件故障后的继发故障(ST状态或LT状态下的继发故障)。ND状态发生时系统通常包含多个故障，因此也具有完全维修与不完全维修2种维修方案[18]。图1给出了采用完全维修策略时典型发动机控制系统TLD分析的马尔可夫状态转移图。

图1中，LT(j)(j=1,2,…,n)为第j个LT状态；ST(i)(i=1,2,…,m)为第i个ST状态；ND(w)(w=1,2,…,l)为LT状态继发故障导致的ND状态；ND(w)(w=l+1,…,q)为ST状态继发故障导致的ND状态；μLT、μST、μND与μFB分别为系统处于LT(j)、ST(i)、ND(w)与LOTC状态时的修复率，其中μLT=1/TLT,μST=1/TST，由于ND(w)状态与LOTC状态发生时需要立即修复，μND与μFB实际计算时取一个较大的数值；λLT(j)为从完好状态进入第j个LT状态的故障率；λST(i)为从完好状态进入第i个ST状态的故障率；λLT-ND(j)为第j个LT状态继发故障进入ND状态的故障率；λST-ND(i)为第i个ST状态继发故障进入ND状态的故障率；λLT-LOTC(j)为第j个LT状态进入LOTC状态的故障率；λST-LOTC(i)为第i个ST状态进入LOTC状态的故障率；λHMU-UC(j)为λHMU与λUC之和，其中λHMU为导致LOTC事件的所有液压机械组件的故障率之和，λUC为导致LOTC事件的所有电子电气部件的未覆盖故障的故障率之和。

图1 TLD分析的马尔可夫模型Fig.1 Markov model of TLD analysis

2.2 运行成本建模

发动机控制系统TLD运行的成本主要包括4个部分，分别是长时派遣时故障的维修费用CLT、短时派遣时故障的维修费用CST、ND状态导致的损失费用CND以及LOTC状态导致的损失费用CLOTC。

1) 通常LT故障采用周期检查维修策略，即使部件未发生故障，也会产生额外的检查费用。因此，LT状态下故障的单位时间维修费用不仅包括故障部件的单位时间维修费用还包括周期检查的单位时间损失费用。因此，CLT可表示为

(1)

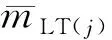
TLD运行中长时派遣时周期检查间隔时间TPIR的近似表达式为[1]

(2)

式中:TMTBF(LT)为长时派遣故障的平均间隔时间，可表示为

(3)

2) 由于ST故障通常采用最低设备清单(MEL)维修策略，此类故障的确切发生时间可以获知，因此不会产生除维修费用以外的损失费用。故CST可表示为

(4)

3) 由于一旦发生ND状态系统需要立即修复，这将导致航班延误。因此，ND状态的损失费用不仅包括故障部件的维修费用还包括飞机延误时的损失费用。故CND可以表示为

(5)

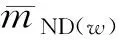
4) LOTC事件的发生会导致推力控制丧失，这不仅会产生航班延误费用，还会产生由于不安全事件导致的其他损失费用，如航空事故调查费用等。故CLOTC可以表示为

(6)

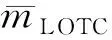
综上所述，TLD运行的单位时间运行总成本可以表示为

(7)

3 基于CTMC的状态稳态频率算法

3.1 系统各状态发生次数求解

令系统的状态空间为E={1,…,i,…,j,…,N}。Mij(t)表示初始时刻从状态i出发，t时间内系统到达状态j的次数。求解Mij(t)的过程如下：

将(0,t+Δt]分解为(0,Δt]和(Δt,t+Δt]这2段。由于充分小的时间Δt内马尔可夫过程中发生2次或2次以上状态转移的概率为无穷小ο(Δt)[19]，故由全概率公式可以得到

(8)

式中：Pik为状态i到k的转移概率。

在Δt内转移概率函数满足：

(9)

式中：qij为状态i到j的转移率。

将式(9)代入式(8)，等式两边同时减去Mij(t)并除以Δt后得到

(10)

当Δt趋近于0时式(10)的右端存在极限，故Mij可微。得到

(11)

式(11)的矩阵形式可以写成

(12)

式中：M′(t)为向量[M′1j(t),M′2j(t),…,M′Nj(t)]T;M(t)为向量[M1j(t),M2j(t),…,MNj(t)]T;A为向量[q1j(t),q2j(t),…,qij(t)]T,i≠j;Q为马尔可夫转移率矩阵，0为分量为0的列向量。

通过解式(12)的微分方程组，即可得到Mij(t)的值。

3.2 系统各状态发生频率求解

令系统初始分布为Pi(0)=[0,…,0,1,0,…,0]，mij(t)为初始时刻处于i状态，t时刻到达状态j的瞬时频率。即

mij(t)=M′ij(t)

(13)

式(13)进行拉普拉斯(L)变换，得到

(14)

结合式(12)可以得到方程组：

(15)

解出式(15)，得到

(16)

则

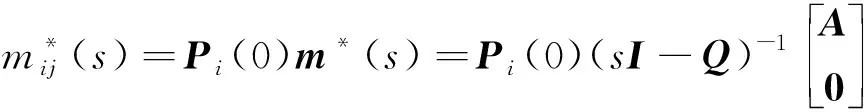
(17)

系统状态概率分布Pi(t)的L变换[20]为

(18)

比较式(17)与式(18)，可得

(19)

由全概率公式及式(19)可得

(20)

因此，得到系统稳态时到达状态j的频率为

(21)

式中：πk为Pk(t)的极限概率。

3.3 TLD分析中各状态的稳态频率

(22)

式中：qk-LT(j)为状态k到第j个LT状态的转移率。

(23)

式中：qk-ST(i)为状态k到第i个ST状态的转移率。

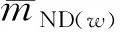
(24)

式中：qk-ND(w)为状态k到第w个ND状态的转移率。

(25)

式中：qk-LOTC为状态k到LOTC状态的转移率。

4 TLD运行的成本优化模型构建

本节以带故障派遣时间间隔TST和TLT为决策变量，以安全性要求以及签派可靠度要求为约束条件，分别建立了TLD运行的单目标与多目标成本优化模型。

4.1 目标函数建立

将式(22)～式(25)代入式(7)可得

(26)

式(26)中的运行成本函数是各状态极限概率与转移率的函数，在马尔可夫过程中，状态极限概率与转移率矩阵的关系[19]为

(27)

由式(27)求得的各状态极限概率是转移率Q的函数，而Q中表示故障修复的转移率是TST和TLT的函数。因此，单位时间运行成本也是TST和TLT的函数。

4.2 约束条件建立

在飞机运营过程中ND状态经常出现，ND状态的发生频率将直接影响飞机的签派可靠度，而签派可靠度是民用飞机重要的可靠性指标，因此，在进行TLD运行成本优化模型建立时，除了考虑安全性约束外，还应将签派可靠度作为约束条件。

1) 平均完整性水平约束条件建立

(28)

式中：Pinto-LOTC(t)为t时刻流入LOTC状态的概率；PLOTC(t)为t时刻处于LOTC状态的概率。

从图1可以看出系统处于稳态时流入LOTC状态的概率为

(29)

式中：πLT(j)、πST(i)及πFU分别为系统处于第j个LT状态、第i个ST状态及FU状态的极限概率。

式(29)也可表示为

(30)

式中：πk为除ND、LOTC状态外的第k个状态的极限概率；qk-LOTC为状态k到LOTC状态的转移率。

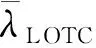
(31)

式中：πLOTC为LOTC状态的极限概率。

2) 签派可靠度约束条件建立

计算TLD分析的签派可靠度时，将FU、LT及ST状态视为工作状态(该状态集合用W表示)，ND状态和LOTC状态视为故障状态(非派遣状态，该状态集合用F表示)。假设马尔可夫模型中状态1～状态i属于W，即W={1,2,…,i}，状态i+1～状态n属于F，即F={i+1,i+2,…,n}。签派可靠度可以表示为[16]

(32)

式中：TFL为飞机的平均航段时间。

由于平均完整性水平和签派可靠度同样是极限概率和转移率的函数，因此平均完整性水平和签派可靠度也是TST和TLT的函数。

4.3 优化模型建立

为了保证系统的可靠性，带故障派遣时间需调整在一定范围之内。因此，TLD运行的单目标成本优化模型可表示为

minCLOSS

(33)

式中：R*为签派可靠度要求；λ*为安全性要求；Tmax为带故障派遣时间最大值。本模型利用遗传算法(Genetic Algorithm, GA)进行求解。

TLD运行的多目标成本优化模型可表示为

min {CLOSS,-RD}

(34)

本模型利用带精英策略的非支配排序遗传算法(Fast Non-dominated Sorting Genetic Algorithm, NSGA-II)，获得TST和TLT的非劣解。

5 实例分析

本部分根据各状态发生次数算法建立了单位时间运行成本函数，利用蒙特卡罗仿真法以简化的某型号发动机控制系统为例，验证了成本函数模型的有效性。并针对某型FADEC系统利用本文所提的运行成本优化方法开展了TLD分析。

5.1 模型验证

式(26)给出的单位时间运行成本是基于马尔可夫过程的状态频率提出的，称之为稳态频率法。为了验证其有效性，利用状态发生次数法和文献[13, 17]提出的蒙特卡罗仿真法分别建立了单位时间运行成本模型。

基于状态发生次数法建立的TLD运行成本模型为

(35)

式中：MLT(j)(t)、MST(i)(t)、MND(w)(t)、MLOTC(t)分别为t时间内第j个LT状态、第i个ST状态、第w个ND状态以及LOTC状态的发生次数，可通过式(12)求得，各状态单位时间的发生次数即为各个状态的频率。同样由于C′LOSS是转移率的函数，因此C′LOSS也是TST和TLT的函数。

在此蒙特卡罗仿真法中，每一次仿真，分别记录ST、LT与ND状态的发生次数并统计相应的维修费用，多次仿真后，当系统单位时间运行成本收敛时，可求得系统单位时间运行成本。

以某型号发动机控制系统为例，该系统简化后包括电子控制组件(Electronic Control Unit, ECU)、电源(PMA)以及HMU等部件，系统可靠性框图见图2。

图2 简化的发动机控制系统可靠性框图Fig.2 RBD of simplified engine control system

系统中，ECU、PMA、HMU的故障率分别为：8×10-5、2×10-5、6×10-6。该系统采用完全维修策略时TLD分析的马尔可夫模型如图3所示。图中，A表示任一ECU Channel故障，B表示任一PMA Winding故障，AB表示任一ECU Channel故障后任一PMA Winding发生故障，BA表示任一PMA Winding发生故障后任一ECU Channel故障，C表示HMU故障。

图3 图2所示系统马尔可夫模型Fig.3 Markov model of system in Fig. 2

该系统中，ECU、PMA、HMU的维修费用分别为10万元、9万元、2万元；CPIR、CDelay、COther分别为2万元、61万元、39万元；μFB、μND取值均为10/h，表示在0.1 h内修复；TFL取10 h。为了便于计算，取短时派遣时间TST为250 h[21]，式(35) 中t取系统首次故障前平均时间(MTTFF)，不同方法求得的单位时间运行成本变化趋势如图4所示。

从图4可以看出，3种方法计算的单位时间运行成本非常相近，蒙特卡罗仿真法与稳态频率法、状态发生次数法之间的误差都控制在1.33元之内，稳态频率法与状态发生次数法之间的最大误差为0.35元。误差产生的根本原因是状态频率的计算方法不同，图5给出了不同方法求得的各状态频率随TLT的变化趋势。图中，ND状态的频率为马尔可夫模型中2种ND状态频率之和。

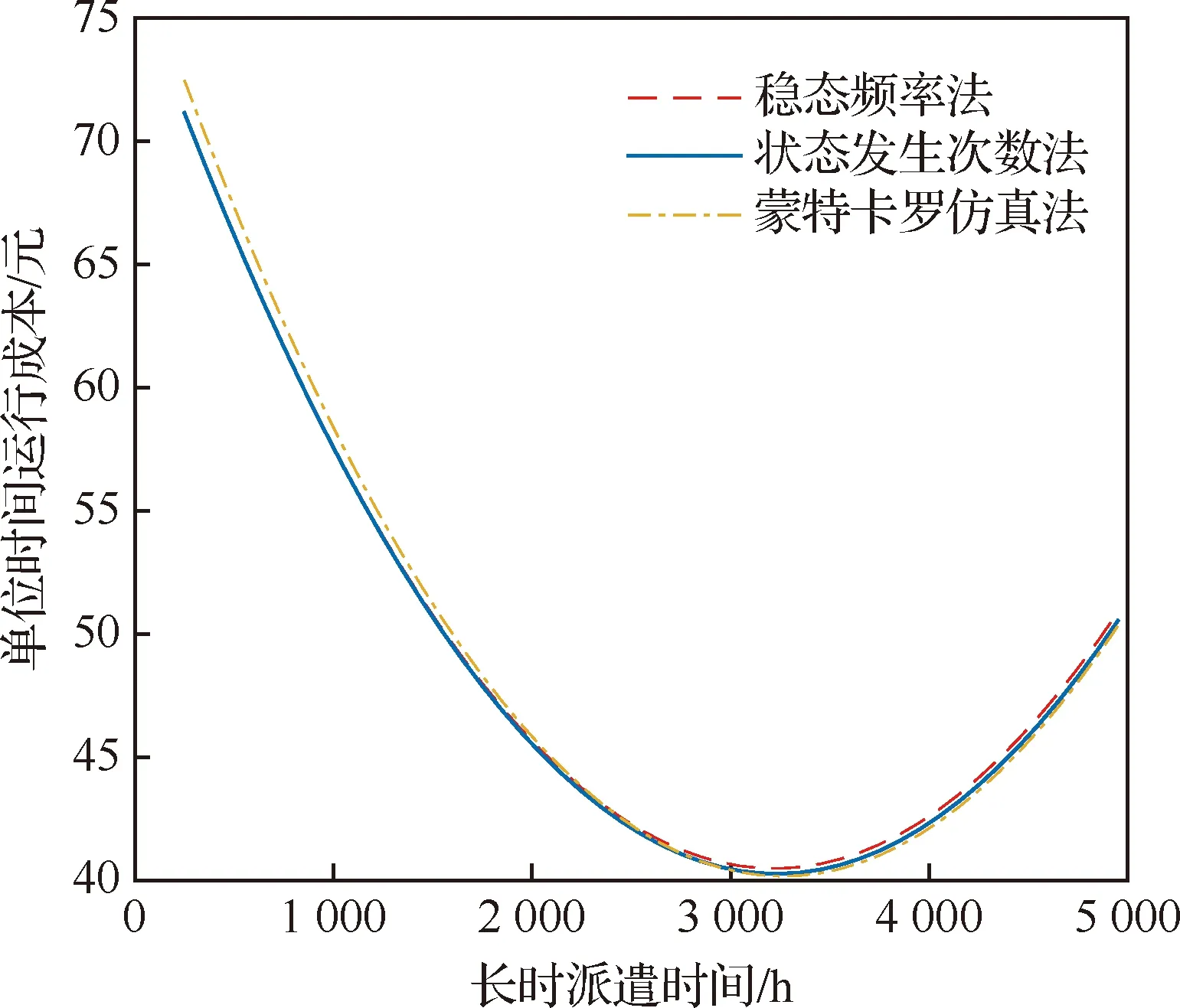
图4 单位时间运行成本对比Fig.4 Comparison of unit time operating cost

从图5中可以看出，稳态频率法与状态发生次数法计算的各个状态频率非常接近，蒙特卡罗仿真法计算的各个状态频率的误差相对较大，但是最大误差仍然在1×10-5以内。由于稳态频率法是系统处于稳定状态时的频率，计算过程中包含了LOTC状态及ND状态的故障修复时间，而这2种状态一旦发生需要立即修复，理论上修复时间为0，因此相较于稳态频率法，状态发生次数法计算的单位时间运行成本更为精确，但是由于此方法计算时需要求解微分方程组，计算过程较为繁琐，而稳态频度法只需要求解简单的代数方程，故稳态频率法计算上更加简便。而且只要在计算过程中将与μFB设置的足够大，那么修复时间就会越小，稳态频率法产生的误差也就足够小。

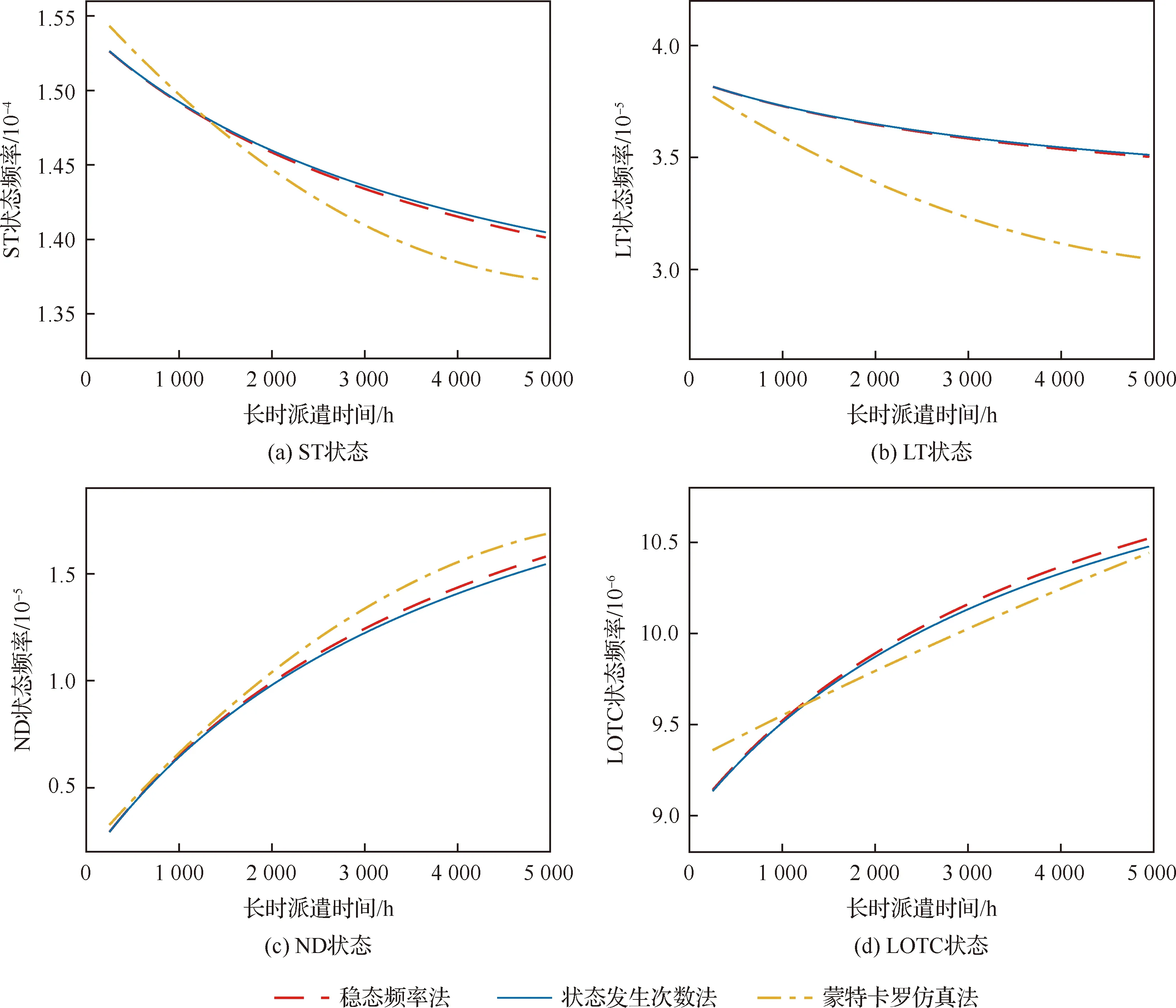
图5 不同方法求得的状态频率Fig.5 State frequencies obtained by different methods

综上所述，利用稳态频率法计算发动机控制系统TLD运行的单位时间成本，方法简便且可以保证计算结果的准确性。

5.2 工程实例

某型FADEC系统由ECU、PMA、HMU、传感器等部件组成，系统结构如图6所示。

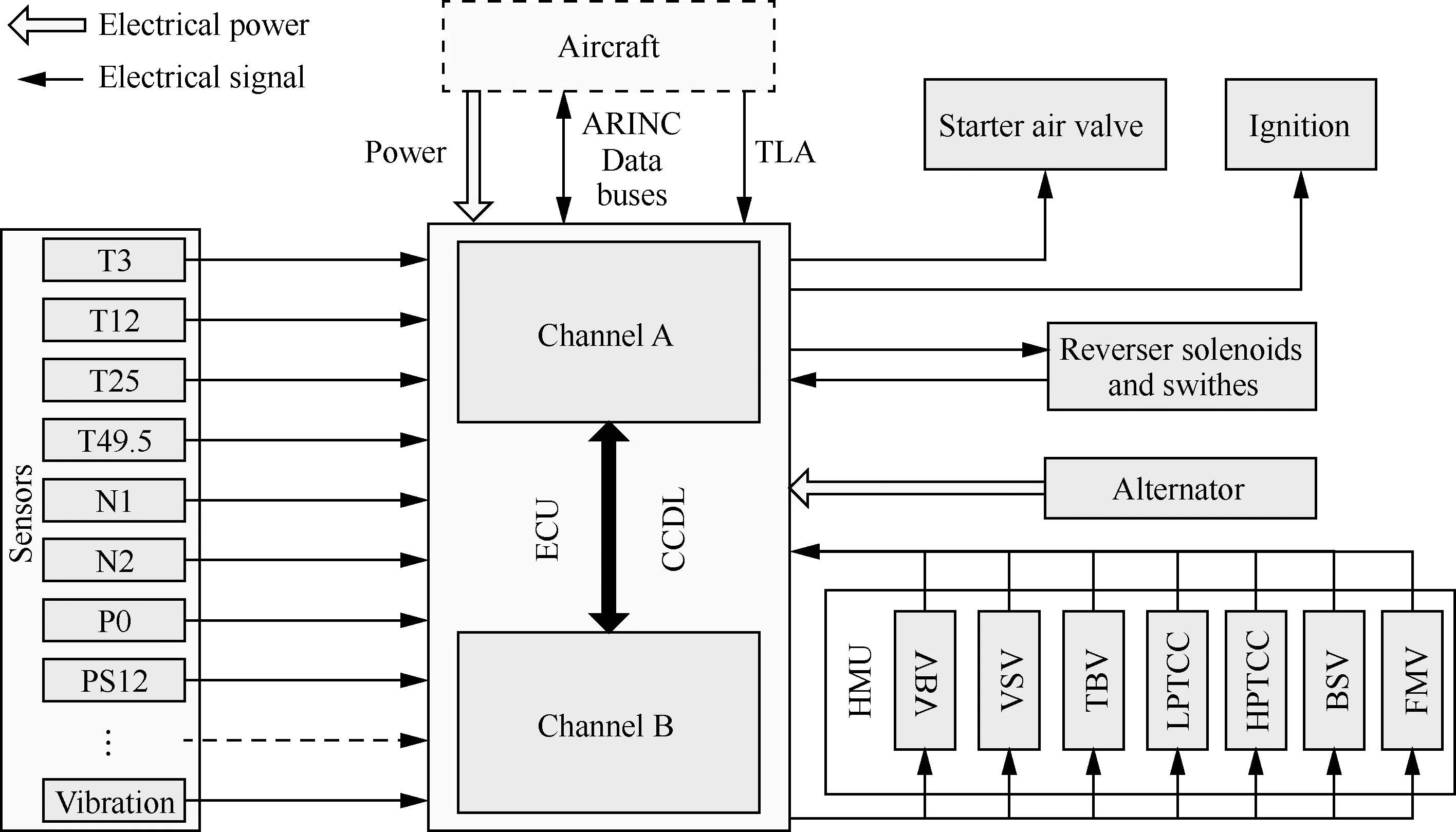
图6 某型FADEC系统结构Fig.6 Structure of FADEC system

ECU由2台名为通道(Channel)A与通道B的电子计算机组成，通道A与B通过交叉通道数据链(Cross Channel Data Link, CCDL)进行通讯，主要功能是实现发动机控制计算并且监控发动机状态。2个通道均接受来自专用PMA的交流电电源。其中通道A接受来自专用PMA电磁线圈(Winding)A中的交流电源，通道B接受来自专用PMA电磁线圈B中的交流电源，专用PMA的线圈A与B是独立的。HMU将源于ECU的控制指令转换为液压压力，驱动燃油计量活门(Fuel Metering Valve, FMV)实现燃油控制，驱动可变静子叶片(Variable Stator Vane, VSV)与可变放气活门(Variable Bleed Valve, VBV)实现压气机气流控制。ECU计算FMV、VSV以及VBV控制指令所需输入信号包括：高压转子转速(N2)、压气机排气温度(T3)、油门杆角度(Thrust Lever Angle, TLA)以及HMU中执行机构的位置反馈信号[14, 22]。

在TLD分析中只考虑与LOTC相关的功能，在FADEC系统的所有功能中，燃油控制功能丧失会直接导致发生LOTC事件，压气机气流控制功能丧失会影响压气机失速特性并引起不可接受的推力振荡，也会导致发生LOTC事件，其他功能均不会导致发生LOTC事件。因此开展TLD分析只需针对部件ECU、PMA、HMU、VBV、VSV、TLA、FMV、N2与T3建立可靠性模型，各部件的故障率及维修费用如表1所示，表中部件的故障率主要参考了文献[17]，并基于某航空公司的实际失效数据对故障率进行了修正。

表1 系统部件故障率及维修费用Table 1 Failure rates and repair costs of components

由于本系统单元众多，无法给出包含所有故障状态的马尔可夫模型，因此本文给出了一种与单故障马尔可夫类似的状态简约马尔可夫模型，如图7所示。由于任一ECU Channel或任一PMA Winding故障都会极大地影响飞机的安全裕度，所以将ECU Channel或PMA Winding故障视为ST状态；其他所有电子电气部件的冗余单元故障均为LT状态；当系统的CCDL故障后继发其他电子电气部件冗余单元全部故障(one route)时，系统瞬时LOTC率大于10-4，此时系统处于ND状态。

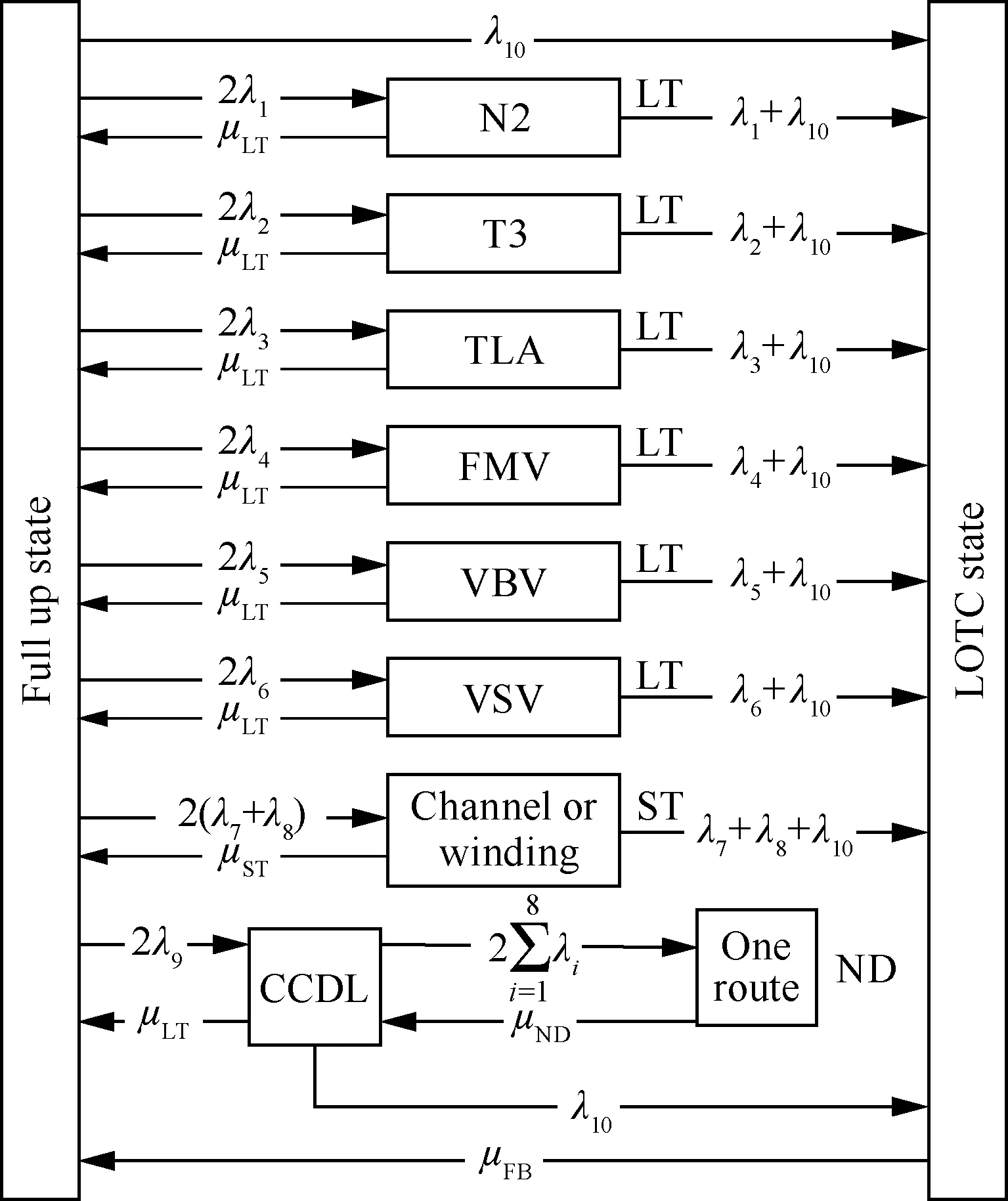
图7 FADEC系统马尔可夫模型Fig.7 Markov model of FADEC system

建立如式(33)的优化模型，其中，CPIR、CDelay、COther分别为5万元、11万元、19万元；μFB、μND取值均为10 h-1；TFL取值为10 h。在签派可靠度要求R*=99.95%、平均完整性水平要求λ*=10-5、带故障派遣时间最大值Tmax=6 000 h的条件下，单位时间运行成本随TST与TLT的变化趋势如图8所示。当TST为255 h，TLT为3 339 h，单位时间运行成本最小，为39.92元，此时签派可靠度为99.952%。

图8 FADEC系统单位时间运行成本Fig.8 Unit time operating cost of FADEC system

建立如式(34)的优化模型，运用NSGA-II算法解决此系统带故障运行时间间隔决策问题，设置算法参数如下：种群数量为200，交叉概率0.9，变异概率0.5，交叉分布指数20，变异分布指数20，经过500次迭代获得Pareto最优集如图9所示。

图9中的每一个蓝色的点代表一个Pareto最优解，各最优解之间没有优劣之分，飞机运营商可根据实际需要选取派遣方案。例如，当飞机运营商给出FADEC系统单位时间运行成本限制时，可根据Pareto最优集得到相应的签派可靠度水平，并确定短时和长时派遣间隔；而不需要重新构建单目标优化模型来进行求解。当给定单位时间运行成本为70 元，可根据Pareto最优集取TST为151 h，TLT为1 023 h，签派可靠度为99.975%。

图9 FADEC系统Pareto最优集Fig.9 Pareto optimal front of FADEC system

6 结 论

本文对发动机控制系统TLD运行下的成本优化方法开展了研究，建立了TLD分析的单目标与多目标成本优化模型，并通过实例验证了方法的有效性。本文完成了以下工作：

1) 建立了考虑ND状态的发动机控制系统TLD分析的马尔可夫模型，推导模型中各状态稳态频率计算方法，构建了系统单位时间运行成本模型。

2) 以带故障派遣时间为决策变量，以安全性要求和签派可靠度要求为约束条件，以系统单位时间运行成本以及签派可靠度为优化目标，分别构建了TLD分析的单目标和多目标优化模型。

3) 利用状态发生次数法和文献中提出的蒙特卡罗仿真法分别建立了单位时间运行成本模型，结合某型号航空发动机控制系统，验证了本文方法的有效性。