基于鲁棒模型的航空交流感应电机预测转矩控制

颜黎明，赵冬冬，焦宁飞

1. 长安大学 汽车学院，西安 710064

2. 西北工业大学 自动化学院，西安 710129

高性能电机驱动系统是航空领域的核心技术和关键装备。在电机控制策略方面，继矢量控制和直接转矩控制之后，契合了电力电子系统开关组合模式及预测控制思想的有限集模型预测控制(Finite Control Set-Model Predictive Control, FCS-MPC)，以其概念直观、动态性能好及易于处理非线性约束等诸多优点，成为电力驱动领域的国际研究前沿[1-6]。FCS-MPC由“预测”和“优化”两阶段组成。在“预测”阶段，基于感应电机离散数学模型及电压矢量计算下一时刻感应电机的系统状态[7-11]。失配的电机参数必然引起预测误差，致使在“优化”阶段无法获取最优的电压矢量，导致系统性能下降甚至失稳。针对上述问题，学者们一方面探究不匹配参数与预测误差之间耦合关系，另一方面则研究不同的补偿策略，以提高模型预测控制的鲁棒性能。

在不匹配参数导致预测误差的理论分析方面，学者们建立了不匹配参数与预测误差间的解析表达式。通过仿真法和实验法定量地研究了两者直接的耦合关系。文献[12]针对三相电压源逆变器，分析了不匹配电阻及电感参数在不同负载条件下对定子电流矢量预测误差的影响关系。文献[13]针对永磁同步电机驱动系统，建立了不匹配电阻及电感参数与电磁转矩预测误差的解析表达式，并提出了基于上一采样时刻电流预测误差的补偿策略，减小了电磁转矩脉动，提高了系统的鲁棒性。文献[14]提出了一种基于扰动观测器及电感参数在线辨识的增强型预测转矩控制。

在预测控制的鲁棒性能提升方面，一些学者提出将失配参数引起的预测误差当做系统扰动，基于自抗扰控制理论或扰动前馈补偿理论抑制预测误差[15-17]。文献[18]提出了一种基于扰动前馈补偿的感应电机预测转矩控制，详细地阐述了扰动观测器的设计方法及预测转矩控制的鲁棒性能。文献[19]提出了一种基于广义比例积分观测器的感应电机鲁棒预测电流控制，电流预测误差由观测器实时估计并采用前馈补偿的方式，提高了系统的鲁棒性。文献[20]融合了自抗扰控制技术和模型预测转矩控制，在转速环采用自抗扰控制抑制转矩环产生的电磁转矩预测误差，实验结果验证了该方法的有效性。

此外，另一些学者则将FCS-MPC与在线参数辨识技术融合起来，基于参数在线辨识技术实时更新预测模型，以提高定子电流或电磁转矩的预测精度。文献[21]提出了一种融合最小二乘法参数辨识技术的永磁同步电机预测转矩控制。文献[22]提出了一种融合模型参考自适应理论的永磁同步电机模型预测转矩控制。文献[23]提出了一种基于递推最小二乘算法的模型预测电流控制，实现了无刷同步起动/发电机在励磁突变情况下的起动控制，并通过调整遗忘因子以跟踪主电机参数的快速变化。文献[24]针对三相PWM整流器提出了一种在线电感参数辨识的直接预测功率控制法。上述方法多从被动方式抑制或消除不匹配参数引起的预测误差，尚未从模型自身的抗扰性出发，建立具有自抗扰性的鲁棒模型。

一些学者提出利用比例积分调节器校正预测模型误差。在文献[17]中，针对永磁同步电机模型预测转矩控制，提出了改进型转矩预测模型，此方法直接依据电磁转矩跟踪误差构建基于PI调节器的误差补偿器。在文献[25]中，针对储能逆变器，提出了一种基于输出误差积分量和状态预测值的全维状态反馈控制策略。文献[26]提出了一种基于预测误差校正的永磁同步电机预测电流控制，此方法将电流预测值与比例系数之积直接补偿到下一步的预测值上，提高了电流的预测精度。本文针对感应电机预测转矩控制，首先深入地研究了失配参数对电磁转矩预测精度的影响规律，建立了定子电流和磁链的闭环预测模型，探讨了闭环模型的参数设计方法，并通过实验验证了所提方法的有效性。

在传统预测转矩控制中，预测模型由感应电机微分方程经一阶向前欧拉法离散获得，此预测模型是一种开环的预测模式。为抑制失配参数引起的预测误差，提高预测转矩控制的鲁棒性，本文提出了基于鲁棒模型的感应电机预测转矩控制系统。其中，鲁棒模型是一种闭环的预测模式，其基本思想来源于反馈控制理论，利用反馈机制提高系统的抗扰性能。本文的安排如下：第1节介绍感应电机数学模型及传统预测转矩控制，第2节阐述鲁棒模型的构造方法及稳定性分析，第3节通过动态性能、稳态性能及参数鲁棒性能3方面对比传统预测转矩控制(Traditional Predictive Torque Control, TPTC)及基于鲁棒模型的预测转矩控制(Robust Model based-Predictive Torque Control, RMB-TPC)。

1 感应电机数学模型及传统预测转矩控制

基于空间矢量理论的感应电机数学模型为

(1)

(2)

(3)

式中:ψs和ψr为定子磁链和转子磁链，其中ψs=Lsis+Lmir、ψr=Lmis+Lrir;is和ir为定子电流和转子电流;Rs和Rr代表定子电阻和转子电阻;Ls、Lr及Lm分别为定、转子电感及励磁电感;ωr为转子转速;vs为两电平逆变器的电压矢量。

在感应电机预测转矩控制中，在“预测”阶段，基于一阶欧拉法离散化后的预测方程为

ψs(k+2)=ψs(k+1)+Tsvs(k+1)-

RsTsis(k+1)

(4)

(5)

(6)

在“优化”阶段，基于评价函数选择使其最小的电压作为最优电压，并在下一时刻施加此最优矢量。在传统的预测转矩控制中，评价函数包含电磁转矩跟踪及定子磁链幅值跟踪，具体为

λψ||ψs|*-|ψs(k+2)||

(7)

传统预测转矩控制框图及执行序列图如图1 所示。由图1及预测方程可知，此模型是一种开环模式，不能抑制失配参数引起的预测误差。

图1 传统预测转矩控制Fig.1 Traditional predictive torque control

图2 失配参数对定子磁链预测误差和电磁转矩预测误差的影响规律Fig.2 Influence of mismatch parameters on stator flux prediction error and prediction error of electromagnetic torque

2 RMB-TPC的构造原理及分析

RMB-TPC的框图和执行序列如图3所示。其中，“鲁棒模型”是由基于闭环模型的定子电流预测和基于离散混合模型的定子磁链预测组成。

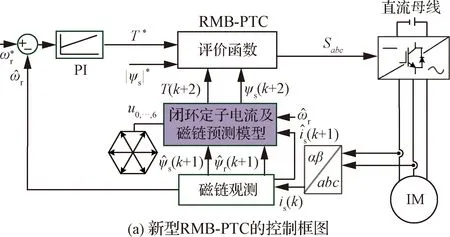
图3 基于鲁棒模型的预测转矩控制Fig.3 Robust model based-predictive torque control

2.1 基于闭环模型的定子电流预测

基于式(1)～式(3)可推导出以定子电流及转子磁链为状态变量的定子电流方程，如下：

(8)

为消除定子电流开环预测方程(5)无法抑制预测误差扰动的缺点，本文提出的闭环模式的定子电流预测方程为

(9)

在式(9)中，补偿项vsum的表达式为

vsum(k+1)=(k1+Tsk2)is_error(k+1)-

ψr(k+1)

(10)

其中:k1和k2为比例系数及积分系数,is_error(k+1)为定子电流预测误差，由方程

(11)

(12)

在本文中n=2。闭环模式的定子电流预测框图如图4所示。

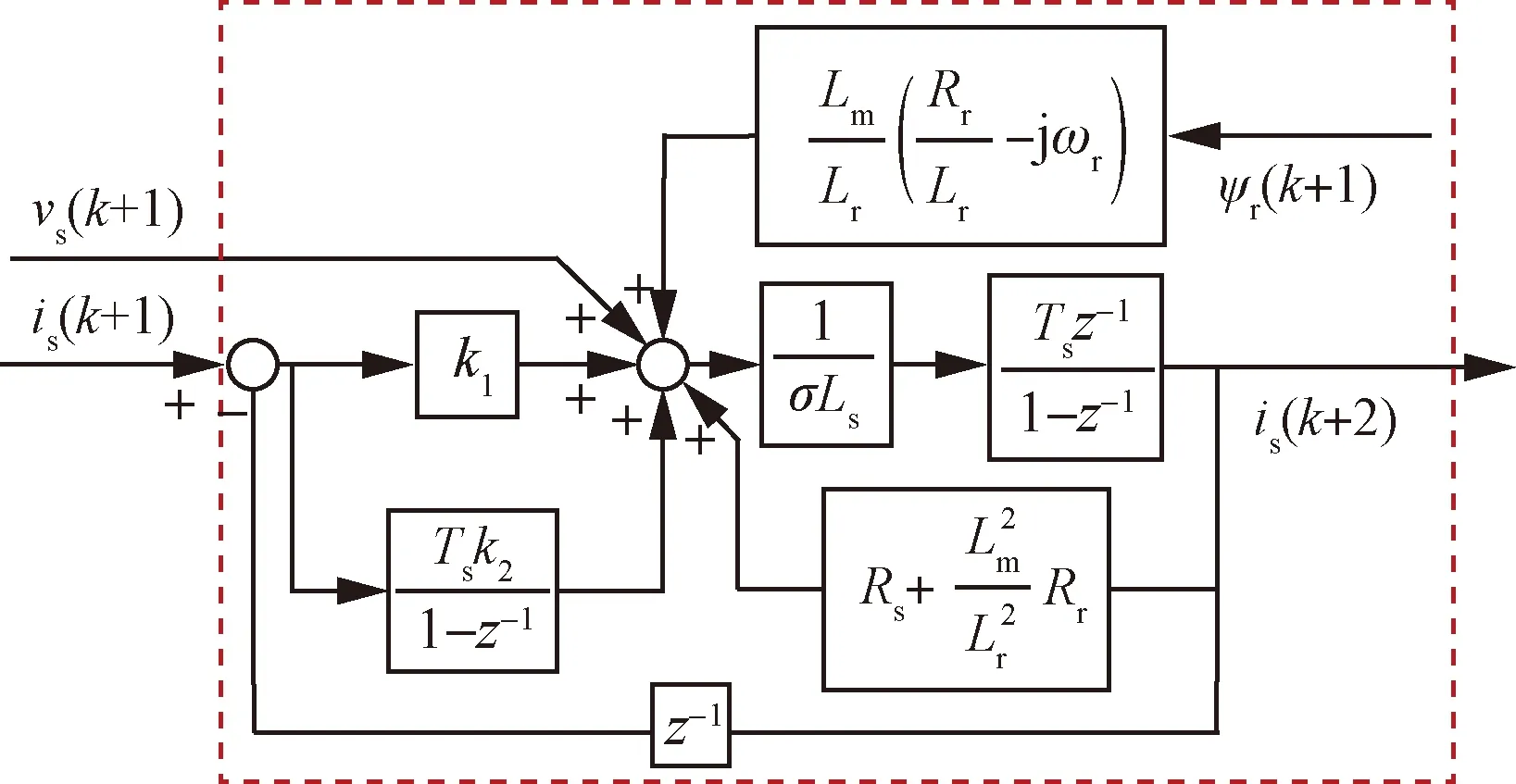
图4 基于闭环模型的定子电流预测框图Fig.4 Diagram of stator current prediction based on closed-loop model

2.2 定子磁链的两种预测模型

感应电机定子磁链矢量可由电流模型计算得到。在以任意速度ω旋转的坐标系，基于定子电流矢量的转子磁链方程为

(13)

式中:ωr为转子速度。为消除方程中转速ωr变量的影响，令ω=ωr，则可得到在转子旋转坐标系下的转子磁链方程。

(14)

基于一阶欧拉法(Tsz-1/1-z-1)可得到离散化的转子磁链方程，

(15)

式中:Ts为离散系统的采样周期。因此，通过旋转变换方程

(16)

依据定子磁链与转子磁链的关系，可获取定子坐标系下定子磁链的解析表达式为

(17)

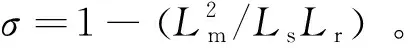
图5 基于电流模型的定子磁链预测Fig.5 Diagram of stator flux prediction based on current model

定子磁链矢量预测的另一种方法是电压模型，多应用于传统的感应电机模型预测转矩控制中，具体的离散化定子磁链预测方程为

RsTsis(k+1)

(18)

依据定转子磁链的关系，可获取转子磁链矢量的解析表达式为

(19)

图6为基于电压模型的定子磁链矢量预测框图，其中Tsz-1/1-z-1代表向前欧拉离散法。

图6 基于电压模型的定子磁链预测Fig.6 Diagram of stator flux prediction based on voltage model

2.3 基于离散混合模型的定子磁链预测

为提高定子磁链预测的鲁棒性，本文提出了融合电压模型和电流模型的定子磁链离散混合模型，电压模型到电流模型的切换由比例积分调节器控制。定子磁链离散混合模型和定子电流闭环模型共同组成鲁棒模型，具体框图如图7所示。虚线框内为定子磁链离散混合模型的调节器，k3和k4分别为比例系数及积分系数。在图7中，补偿项的差分方程为

图7 鲁棒预测模型的整体框图Fig.7 Diagram of robust prediction model

(20)

因此，带补偿的定子磁链矢量计算公式为

RsTsis(k+1)+Tsvψ_error(k+1)

(21)

2.4 RMB-TPC鲁棒模型的稳定性分析

依据离散系统控制理论，定子磁链离散混合模型的传递函数为

(22)

式中：N1、N2、D1、D2以及D3的表达式为

依据离散系数控制理论，传递函数(22)的特征方程为z2+(P1+P2)z+(P1P2)=0，其中P1P2=(D3/D1)、P1+P2=(D2/D1)。P1=e-2f1Ts和P2=e-2f2Ts为传递函数(22)的极点，f1和f2为离散混合模型的两个根，因此，调节器参数k3和k4可依据两个根的取值设定。

同样地，定子电流闭环模型的传递函数为

(23)

式中：M1、M2、E1、E2及E3的表达式为

同样地，定子电流闭环模型的参数k1和k2可由其特征方程根的取值设定。

在离散域，定子电流闭环模型和定子磁链离散混合模型在不同设计参数下的根轨迹分别如图8 所示。依据控制理论，闭环极点应位于z平面右半单位圆内并尽可能靠近原点。因此，设计参数取值如下：k1=6.0,k2=15.0,k3=7.0,k4=9.0。

图8 定子电流闭环模型和定子磁链离散混合模型的根轨迹图Fig.8 Root locus of stator current closed-loop model and stator flux discrete hybrid model

3 RMB-TPC与T-PTC的实验对比

感应电机驱动系统的实验平台如图9所示，由感应电机、永磁同步电机、驱动模块、控制模块及示波器等部分组成。感应电机参数如下：额定功率PN=2.2 kW、额定电压UN=380 V、额定转速ωN=2 772 r/min、极对数p=1、定子电阻Rs=2.68 Ω、转子电阻Rr=2.13 Ω、定转子电感Ls=Lr=0.283 H、定转子互感Lm=0.275 H。感应电机由数字信号处理器(型号为TMS320F28335)控制，新型RMB-TPC与传统T-PTC的执行算法由C语言编写并在数字信号处理器中运行。永磁同步电机为负载电机，由丹佛斯变频器控制，其主要作用是为感应电机提供负载转矩。感应电机的状态变量由驱动器的数模转换模块输出，并由示波器采集数据，在MATLAB中绘制图形。

图9 感应电机驱动系统实物Fig.9 Experimental platform of induction motor

传统T-PTC及新型RMB-TPC的动态响应如图10所示，电机转速指令在1.0 s由额定值2 772 r/min变为-2 772 r/min。从上至下依次为转速响应、电磁转矩动态响应、定子磁链幅值及定子电流波形。由图可知，与传统的T-PTC相比，新型RMB-TPC具有较快的动态性能及较小的定子电流总谐波含量及较小的定子磁链幅值脉动。

图10 传统T-PTC和新型RMB-PTC的动态性能Fig.10 Dynamic performance of traditional T-PTC and new RMB-PTC

传统T-PTC及新型RMB-TPC的电磁转矩瞬态响应如图11所示。感应电机运行于转矩模式，永磁同步电机运行于转速模式。感应电机的电磁转矩指令在4 ms由0 N·m变为额定值7.5 N·m。

在图11中，从上至下依次为转子转速响应、电磁转矩指令、电磁转矩瞬态响应及逆变器施加>的电压矢量。由图可知，传统T-PTC的电磁转矩瞬态响应时间为0.85 ms，而新型RMB-TPC的电磁转矩瞬态响应时间为0.65 ms。由于新型RMB-TPC精确的电磁转矩预测模型确保了最优电压的选择，因此其具有较快的电磁转矩瞬态响应。

图11 传统T-PTC和新型RMB-PTC的电磁转矩瞬态响应Fig.11 Electromagnetic torque transient response of traditional T-PTC and new RMB-PTC

传统T-PTC及新型RMB-TPC的稳态性能如图12所示。从图可看出，与传统T-PTC相比，

图12 传统T-PTC和新型RMB-PTC的稳态性能Fig.12 Steady state performance of traditional T-PTC and new RMB-PTC

新型RMB-TPC具有更小的定子电流总谐波含量以及更小的电磁转矩脉动。当感应电机转子速度为1 386 r/min，电磁转矩为7.5 N·m时，传统T-PTC的定子电流总谐波含量为12.29%，而新型RMB-TPC的定子电流总谐波含量为9.73%，降低了20.8%。传统T-PTC的电磁转矩脉动为1.6 N·m，而新型RMB-TPC的电磁转矩脉动为1.1 N·m，降低了31.25%。

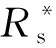
图13 传统T-PTC及新型RMB-TPC的鲁棒性能分析Fig.13 Robust performance analysis of traditional T-PTC and new RMB-TPC

4 结 论

为解决失配参数导致预测误差引起控制性能下降的问题，本文提出了一种基于鲁棒预测模型的感应电机预测转矩控制，得出如下结论：

1) 鲁棒模型由定子电流闭环模型及定子磁链离散混合模型组成，鲁棒模型的反馈机制抑制了失配参数引起的预测误差扰动。

2) 精确的模型预测确保了最优电压矢量的正确选择。实验结果表明，相比于传统的开环预测模型，基于鲁棒模型的预测转矩控制具有更好的动态性能、稳态性能及鲁棒性能。