面向集中力扩散的回转曲面加筋拓扑优化方法

李增聪，陈燕，李红庆，田阔,*，王刚，高峰，王博

1. 大连理工大学 工业装备结构分析国家重点实验室 工程力学系，大连 116024

2. 中国空间技术研究院 总体设计部，北京 100094

航天器中各舱段之间存在大量的回转曲面加筋型连接结构，其主要的功能是将一侧较大的集中力载荷均匀地扩散到另一侧。图1展示了东方红卫星平台[1]通过回转曲面加筋型的对接环结构，将主星结构的集中力载荷均匀地扩散到下面的推进舱结构。为了满足推进舱结构强度要求，需开展对接环结构设计，以实现集中力高效扩散。图2为运载火箭热分离式级间段结构，为了避免贮箱发生局部破坏，通过放射肋形式的短壳结构与贮箱连接进行集中力扩散。传统型放射肋结构形式可以一定程度上起到集中力扩散作用，但为了避免连接处局部强度不足往往采取过于保守的设计，易导致结构超重[2-3]。近年来，航天器结构向大型化、承载重型化的趋势发展。针对对接环、贮箱短壳这类典型的航天器回转曲面加筋结构，如何在大载荷、短距离条件下实现高效的集中力扩散设计，是一个亟待解决的难题。

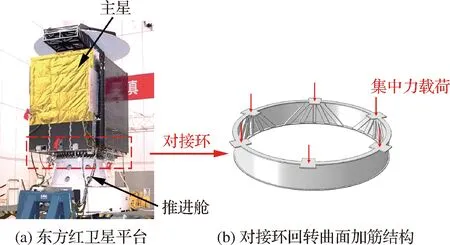
图1 卫星平台对接环结构示意图[1]Fig.1 Schematic diagram of joint ring of satellite platform[1]

图2 贮箱短壳结构示意图[3]Fig.2 Schematic diagram of short shell of tank[3]

拓扑优化方法突破了传统的经验设计和类比设计方法，可以根据载荷条件、约束条件和优化目标，在给定的区域内对材料分布进行优化设计[4-6]。针对集中力扩散问题，学者们开展了拓扑优化方法的相关研究。牛飞等[2,7]基于连续体拓扑优化方法，提出了集中力扩散优化模型，相比传统放射肋设计方法，优化方案的应力分布更加均匀；张家鑫等[3,8]基于拓扑优化、尺寸优化等方法，采用NSGA-Ⅱ(Non-Dominated Sorting Genetic Algorithm Ⅱ)算法建立了考虑集中力扩散的多目标优化模型，得到了分级型放射结构创新构型；西北工业大学张卫红团队[9-11]针对集中力扩散拓扑优化方法也开展了系列研究，将反力方差约束[9,11]、人工杆单元[10]引入拓扑优化方法中，并基于数值算例验证了所提出方法在集中力扩散与输出载荷控制的有效性，并获得创新构型；张晓颖等[12]针对薄壁贮箱结构千吨级集中力扩散问题，开展拓扑优化设计，通过理论分析、有限元计算和试验验证，获得了高效率集中力扩散的结构构型；梅勇等[13]针对运载火箭捆绑联接舱段集中力扩散和轻量化设计，以多工况下最小加权柔度为目标函数进行结构拓扑优化，得到了应力分布均匀且结构减重18.2%的优化结果。尽管上述研究针对简单的平面结构建立了有效的集中力扩散优化模型，但对于大载荷、短距离条件下的回转曲面加筋集中力扩散拓扑优化设计，还较少有学者开展相关工作，其主要面临拓扑优化结果难以满足回转曲面加筋制造工艺要求、拓扑优化结果难以自动化重构两方面挑战。

针对第1个挑战，为了满足机铣等回转曲面加筋制造工艺要求，回转曲面加筋拓扑优化结果需保证筋条与回转曲面蒙皮垂直、筋条沿加工方向保持厚度一致。在拓扑优化方法中，可通过增加约束条件的方式实现这一效果[14]。其中代表性的方法是变量映射方法[15-16]，已被广泛应用于制造工艺约束的实现[17-19]。其通过约束密度变量在加筋方向上的关系，可以得到满足拔模、冲压、机铣等制造工艺要求的拓扑优化结果。变量映射方法在拓扑优化开始之前需要定义映射背景网格区域，并通过邻域搜索来建立单元区域与设计变量之间的映射关系。但对于回转曲面结构，往往难以划分规则的有限元网格，导致变量映射难以实施。因此，研究一种对网格质量要求不高、操作简便的回转曲面加筋特征实现方法，对于建立满足回转曲面加筋制造工艺要求的集中力扩散拓扑优化方法具有重要的研究意义，也是本文的一个研究内容。

针对另一个挑战，根据回转曲面加筋拓扑优化结果进行模型重构是繁琐而耗时的，传统人工建模方式耗时长且精度低，无法实现参数化建模，一定程度上增加了设计周期。根据文献调研[20-21]，目前针对拓扑优化结果的模型重构方法研究尚不成熟，是一个有潜力的研究方向。近年来，网格变形[22-23]方法以其高效、可控和易于自动化等特点在复杂结构的快速建模分析与优化中得到了广泛应用[24-25]。学者们提出了参数映射方法[26-27]、Delaunay图映射方法[28]、NURBS方法[29]与代理模型映射方法等[30]。其中基于代理模型的网格变形方法在复杂问题的映射中展现出了较大的潜力[31]。因此，本文另一个主要研究内容是基于代理模型的网格变形和映射，建立适用于回转曲面加筋拓扑优化结果的模型智能重构方法。

本文内容主要分为4个部分：第1部分介绍了本文提出的面向集中力扩散的回转曲面加筋拓扑优化方法；第2部分针对对接环结构进行算例研究，验证所提出方法的有效性；第3部分讨论了网格类型和支反力约束上限对优化结果的影响，并将本文提出方法与传统设计方法进行对比总结，同时讨论了网格变形方法的应用范围及优势；第4部分为结论与展望。

1 面向集中力扩散的回转曲面加筋拓扑优化方法

1.1 基于各向异性过滤的集中力扩散拓扑优化方法

在拓扑优化中，过滤方法通常用于解决棋盘格和网格依赖性问题。代表性地，Sigmund等[32]提出了敏度过滤方法，Bourdin[33]提出了密度过滤方法。为了获得满足制造工艺要求的创新构型方案，受文献[34-35]启发，本文提出了一种基于各向异性过滤技术的回转曲面加筋拓扑优化方法，即通过定义Helmholtz方程[36]中的各向异性过滤半径，使沿加筋高度方向的过滤半径大于其他方向的过滤半径，并大于加筋高度的实际结构尺寸，使得回转曲面拓扑优化结果呈现出蒙皮加筋的效果。主要步骤如下：

步骤1建立回转曲面结构有限元模型，定义局部坐标系和各向异性过滤半径

如图3所示，定义结构的局部笛卡尔坐标系XYZ，其中加筋方向(机铣加工方向)设定为局部坐标系的Z向，垂直于加筋方向分别设置为X向和Y向。根据局部坐标系，定义各向异性过滤半径，使沿加筋高度方向的过滤半径rn大于面内方向的过滤半径rt1和rt2，并大于加筋高度的实际结构尺寸，rt1和rt2分别表示方向为沿X方向和沿Y方向的过滤半径。

图3 各向异性过滤半径示意图Fig.3 Schematic diagram of anisotropic filter radius

步骤2建立集中力扩散拓扑优化列式

根据平衡方程,f=Ku

(1)

式中：K表示整体刚度矩阵；f表示节点力向量；u表示节点位移向量。将矩阵分块，则式(1)可以写为

(2)

式中：fc表示外力载荷；fs表示节点的反力；下标s和c分别表示约束自由度和非约束自由度。

式(2)可写为

(3)

基于SIMP[37-38](Solid Isotropic Material with Penalization)材料惩罚模型，以最小化结构应变能作为优化目标，各支座支反力和体分比为约束，建立拓扑优化列式：

(4)

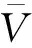
(5)

式中：δjk的维度与位移向量保持一致，在第k个分量取1，其余值为0。

步骤3建立并求解Helmholtz方程

首先，将各向异性过滤定义为一个隐式的Helmholtz方程：

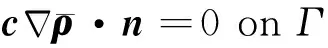
(6)

(7)

式中：V为局部坐标系3个方向的空间基底矢量的矩阵形式；vn为加筋方向；vt1和vt2为垂直于加筋方向。

将式(6)表达成弱形式：

(8)

由于单元密度值在单元上为常量，将Helmholtz方程的单元矩阵He表达为

(9)

式中：N为形函数；Ωe为单元e的空间域。本文方法中Helmholtz方程的单元与有限元计算的单元相同。

步骤4进行各向异性过滤与Heaviside函数过滤

基于过滤矩阵H进行各向异性过滤:

(10)

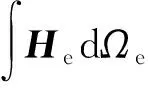
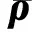
(11)

步骤5开展灵敏度分析，求解优化问题

目标函数对设计变量的灵敏度为

(12)

体积约束灵敏度为

(13)

式中：ve为常量，通常设为1。

各支座支反力约束灵敏度可表示为

(14)

引入伴随向量λ，由式(5)可得

(15)

(16)

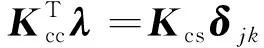
根据灵敏度分析结果，基于移动渐近线法[40](Method of Moving Asymptotes, MMA)对拓扑优化问题进行求解，优化迭代过程重复步骤4与步骤5，直至收敛。

1.2 基于网格变形的拓扑优化结果智能重构方法

对于回转曲面加筋拓扑优化结果的特征提取，传统方法通常是在Solidworks、Unigraphics(UG)等CAD建模软件中进行人工建模。当回转曲面加筋优化结果细节复杂时，其模型重构步骤繁琐、耗时长且准确度低。将CAD模型导入CAE有限元软件时，容易产生网格划分失败、网格单元畸形等问题。针对这一问题，本节提出了一种基于网格变形技术的回转曲面加筋拓扑优化结果智能重构方法，通过预先训练简单结构背景网格域和目标网格域，得到两者之间的映射关系，从而将回转曲面加筋优化结果的有限元模型映射成平面加筋壳，以便于拓扑优化结果的特征提取与重构。如图4所示，所提出方法主要包括以下步骤：

步骤1定义背景网格域和目标网格域，如图4(a)所示，建立回转曲面结构的有限元模型作为背景网格域；如图4(b)所示，建立平面结构的有限元模型作为目标网格域，且保证其包含待建加筋结构的设计空间。

步骤2基于径向基函数(Radial Basis Function，RBF)代理模型[41]，训练背景网格域和目标网格域这两个控制点集，获得二者之间的映射关系(正向与逆向)，以背景网格域网格节点的坐标值为输入，以目标网格域网格节点的坐标值为输出，每个节点包含x、y、z3个方向的坐标值，基于代理模型对坐标值数据进行拟合，获得映射关系。

步骤3基于正向映射关系，将拓扑优化结果展开为平面加筋壳有限元模型，针对回转曲面加筋壳拓扑优化结果的有限元模型(图4(c))，通过步骤2得到的正向映射关系进行网格变形，获得平面加筋壳的有限元模型，如图4(d)所示。

步骤4针对平面加筋壳进行加筋拓扑特征提取，相较于回转曲面加筋壳，平面加筋壳更易于建模，传统建模方式可以快速且准确地对步骤3获得的平面加筋壳有限元模型进行特征提取，且平面加筋壳建模可考虑制造工艺约束。对提取结果划分有限元网格，结果如图4(e)所示。

步骤5基于逆向映射关系，将提取的平面加筋壳有限元模型映射为回转曲面加筋壳有限元模型，将步骤4中的平面加筋壳模型进行网格划分获得有限元模型，通过步骤2得到的逆向映射关系进行网格变形，获得回转曲面加筋壳的有限元模型，结果如图4(f)所示。

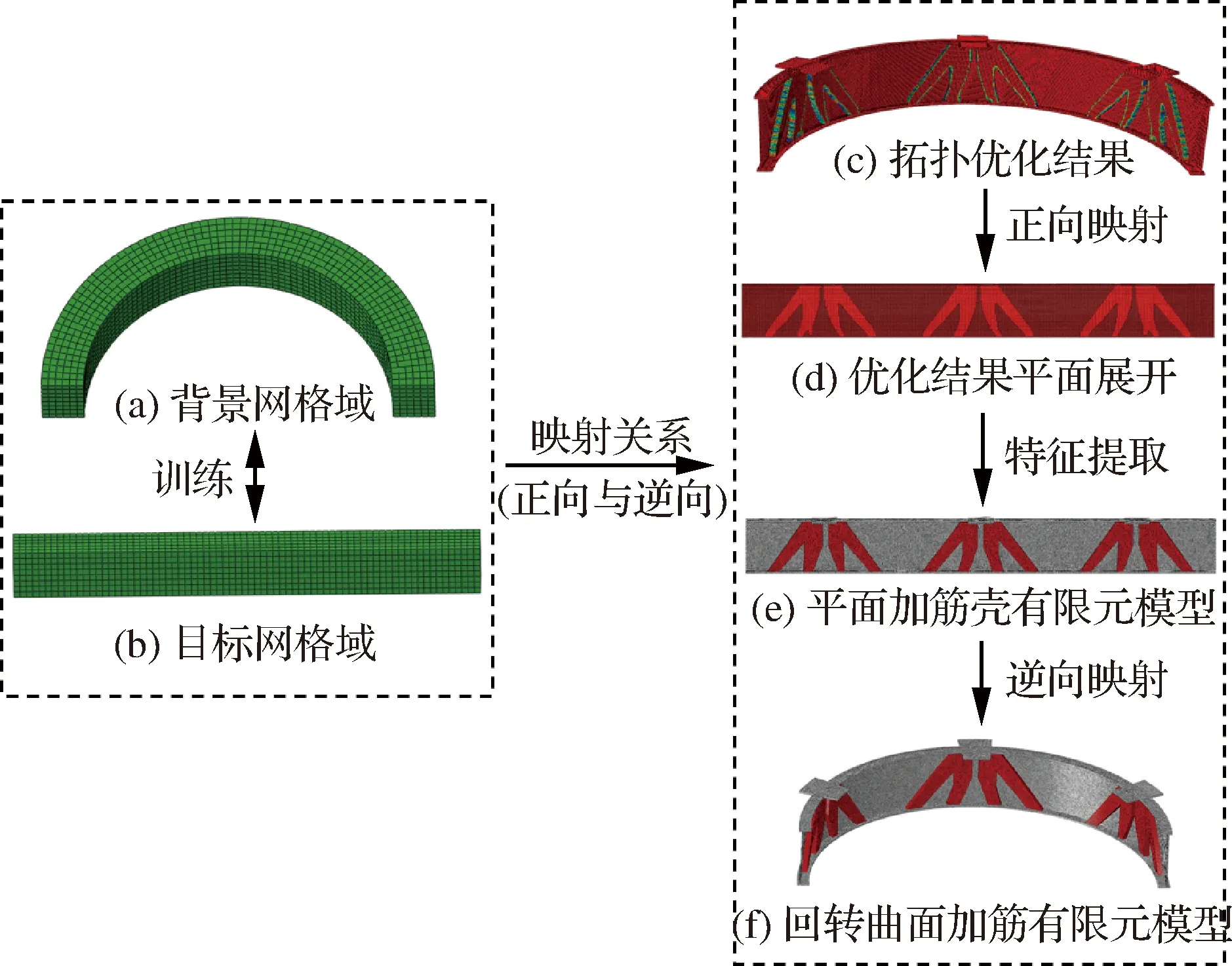
图4 基于网格变形的拓扑优化结果智能重构方法Fig.4 Intelligent reconstruction method for topology optimization result based on mesh deformation

上述方法的“智能”主要体现在加筋构型重构过程中平面与曲面的相互映射。人工手动操作只需在平面上进行加筋建模，这是相对简单且便捷的，对于重构后的平面模型，通过逆向映射关系可将平面加筋构型快速、高效地变为回转曲面加筋构型。

1.3 面向集中力扩散的回转曲面加筋拓扑优化方法

结合1.1节提出的基于各向异性过滤的集中力扩散拓扑优化方法和1.2节提出的基于网格变形技术的拓扑优化结果智能重构方法，本节给出了面向集中力扩散的回转曲面加筋拓扑优化方法，如图5所示，所提出方法的流程主要包括以下两个步骤：

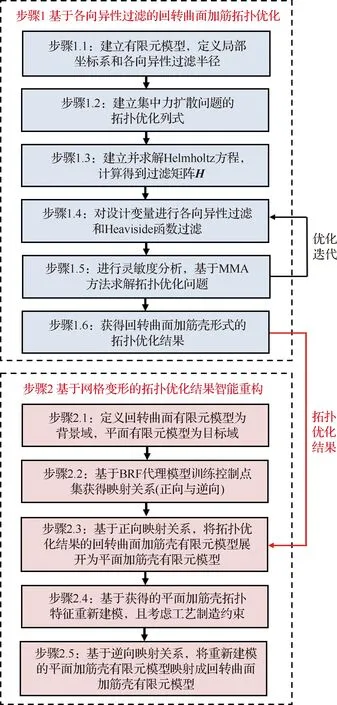
图5 面向集中力扩散的回转曲面加筋拓扑优化方法Fig.5 Topology optimization method for concentrated force diffusion on stiffened curved shell of revolution

步骤1基于各向异性过滤技术开展回转曲面加筋的集中力扩散拓扑优化。步骤1.1建立回转曲面结构有限元模型作为拓扑优化设计域，并设定局部坐标系，定义各向异性过滤半径，使沿加筋高度方向的过滤半径大于面内方向的过滤半径；步骤1.2，基于SIMP材料惩罚模型建立集中力扩散问题的拓扑优化列式；步骤1.3，建立并求解Helmholtz方程，计算得到过滤矩阵H；步骤1.4，对设计变量进行各向异性过滤和Heaviside函数过滤；步骤1.5，对目标函数和约束函数进行灵敏度分析，并基于MMA方法求解拓扑优化问题；步骤1.6，经过优化迭代，获得回转曲面加筋壳形式的拓扑优化结果。

步骤2基于网格变形方法对回转曲面加筋拓扑优化结果进行模型智能重构。步骤2.1，定义回转曲面结构有限元模型作为背景网格域，简单平面结构有限元模型作为目标网格域；步骤2.2，通过RBF代理模型训练两个域的控制点集，获得两者的映射关系(正向与逆向)；步骤2.3，基于正向映射关系对步骤1.6获得的回转曲面加筋壳的拓扑优化结果进行网格变形，获得平面加筋壳的有限元模型；步骤2.4，基于平面加筋壳的有限元模型进行特征提取，且考虑制造工艺要求，得到平面加筋壳的拓扑优化重构结果；步骤2.5，基于逆向映射关系，对重构后的平面加筋壳有限元模型进行网格变形，获得回转曲面加筋壳的有限元模型，即创新结构方案。

2 对接环算例研究

2.1 对接环结构回转曲面加筋拓扑优化设计

以图1中所示的对接环结构为例对本文提出方法进行验证。对接环模型细节如图6所示，主要包括上端框、蒙皮、设计域和下端框4个部分。其中，实际设计要求是在设计域内进行加筋设计，并通过机铣方式进行加工。根据结构的对称性，选择1/2模型作为研究对象。蒙皮厚度为2 mm，设计域厚度为18 mm，设计域高度为200 mm，下端框厚度为5 mm，上端框厚度为7 mm。加载和边界条件如图7所示。在上端框的3三个加载面中心点处分别施加F=70 000 N的集中力，并将中心点自由度与加载面上其余节点的自由度耦合。下端框底部的15个面作为结构支座进行固支约束，支座的位置分布和尺寸参数情况如图8所示。其中3个加载面分别位于3号支座、8号支座和13号支座正上方。由于考虑了对称性，在1/2模型的边界处施加对称边界条件。

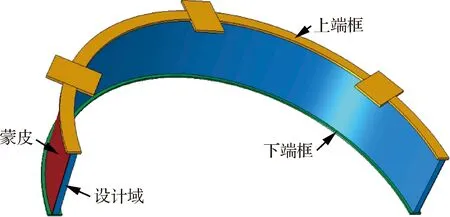
图6 对接环结构示意图Fig.6 Schematic diagram of docking ring structure

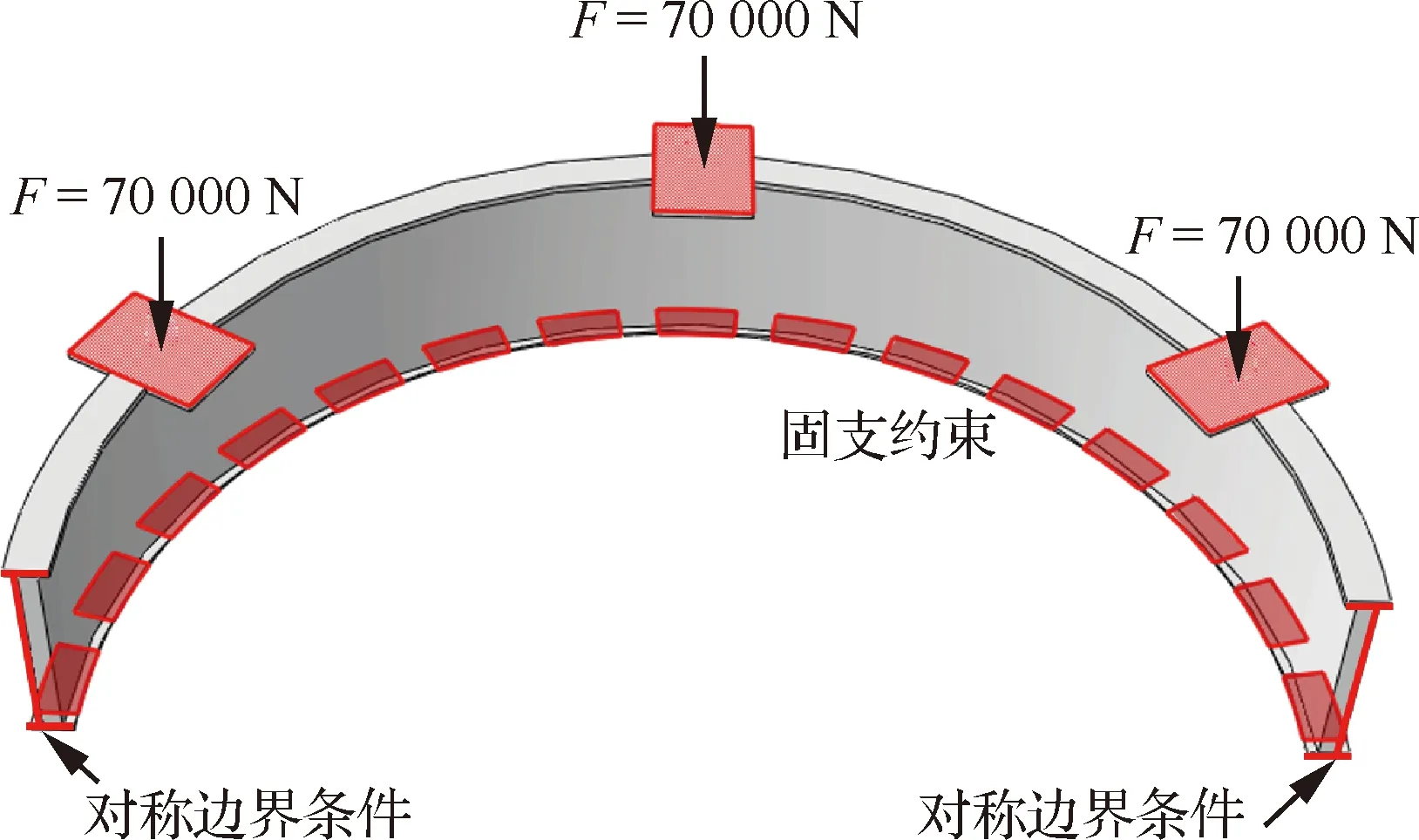
图7 对接环有限元模型示意图Fig.7 Schematic diagram of FE model of docking ring

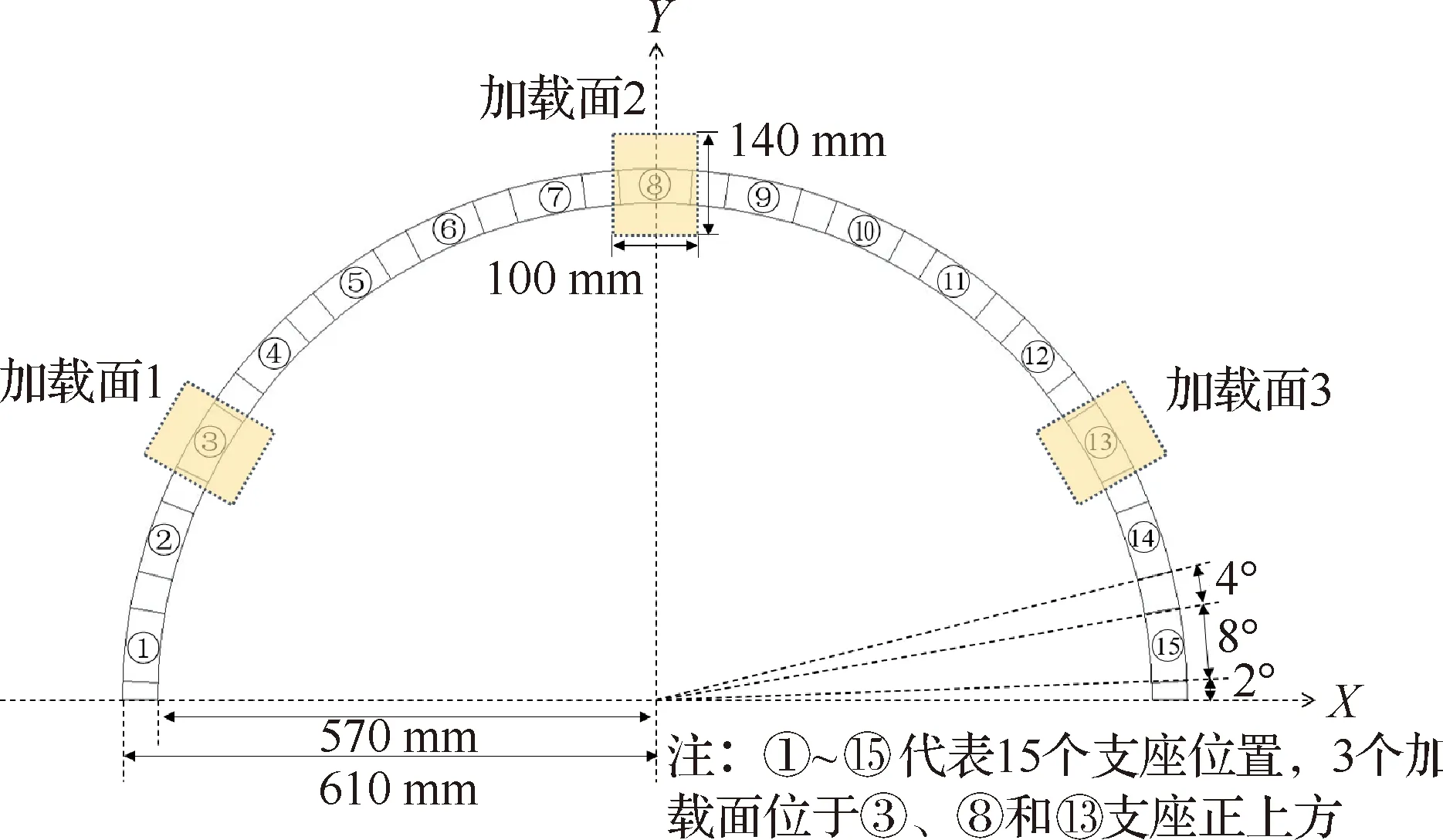
图8 底部支座分布示意图Fig.8 Schematic diagram of distribution of bottom supports

用六面体网格对对接环结构进行单元划分，网格数目为155 600，其中设计域网格数目为114 700。结构材料为铝合金，其杨氏模量和泊松比分别为70 GPa和0.3，屈服强度为325 MPa，材料密度为2 700 kg/m3，模型质量为10.8 kg。

首先，对结构开展基于各向异性过滤的回转曲面加筋拓扑优化，优化目标为最小化结构应变能，支反力约束为结构各支座的支反力均小于20 000 N，体分比上限约束设置为0.3。根据1.1节中的各向异性过滤方法，加筋高度方向的过滤半径rn设置为150 mm，非加筋方向的过滤半径rt1和rt2设置为20 mm，优化最大迭代步数为50步。优化迭代过程及优化目标的迭代曲线如图9所示，图中结构设计域内红色区域代表密度为1的单元，蓝色区域代表密度为0的单元，绿色区域为灰度单元。由图中可以看到，拓扑优化目标函数值随着迭代步数增加逐渐减小并最终收敛，拓扑结果中灰度单元逐渐减少，最终得到拓扑构型清晰、蒙皮加筋形式明显的优化结果。

图9 拓扑优化目标函数迭代过程Fig.9 Iterative process of objective function in topology optimization

2.2 对接环拓扑优化结果模型智能重构与验证

基于网格变形技术的智能重构方法对2.1节获得的拓扑优化结果进行模型重构。首先，以回转曲面结构有限元实体模型作为背景网格域(共包含4 725个有限元节点)，简单平面结构有限元实体模型作为目标网格域(同样包括4 725个有限元节点)，基于RBF代理模型训练两个域的控制点集，获得两者的映射关系。在此基础上，将图9 中的优化结果只保留红色的加筋构型和不可设计域，获得回转曲面加筋壳拓扑优化结果(图10(a))，并开展正向映射，获得平面加筋壳的有限元模型(图10(b))。然后，对平面加筋壳的拓扑特征进行建模，并考虑制造工艺约束，获得平面加筋壳的拓扑优化重构结果(图10(c))。接下来对重构模型划分网格，得到平面加筋壳的有限元模型(图10(d))。最后，再次通过网格变形方法，基于逆向映射获得回转曲面加筋壳的有限元模型(图10(e))。

图10 基于网格变形的拓扑优化结果智能重构示意图Fig.10 Schematic diagram of intelligent reconstruction of optimal result based on mesh deformation

进而，针对回转曲面加筋壳的有限元模型开展集中力载荷作用下的静力学分析，结构的应力云图如图11所示。由图可知结构的整体应力水平较低，最大应力为194.3 MPa，小于屈服强度325 MPa，未发生强度破坏，强度裕度充足。提取各支座约束面的所有节点支反力并分别求和，可以得到各支座的支反力分布情况，结果如表1所示。由表中可以看到，本文方法得到的优化结果各支座的支反力均小于20 000 N，满足集中力扩散的设计要求(20 000 N)。此外，重构模型获得了清晰的回转曲面加筋构型，满足回转曲面加筋机铣制造工艺要求，验证了所提出的拓扑优化方法对于此类回转曲面加筋集中力扩散问题的有效性。

图11 本文方法优化结果重构模型应力分布图Fig.11 Stress distribution diagram of reconstructed model for optimal result by proposed method

表1 本文方法与放射肋方法各支座反力计算结果Table 1 Reaction forces results of supports by proposed method and radial rib method

3 对比与讨论

为了验证本文方法在加筋构型清晰、满足回转曲面加筋制造工艺要求、集中力扩散效率高、网格质量依赖性低等方面的优势，本节首先讨论了网格类型与支反力约束对优化结果的影响，进而对比研究本文方法结果与传统放射肋结果。最后，对所提出网格变形方法的适用范围和优势进行了讨论。

3.1 网格类型与支反力约束对优化结果的影响

本节先讨论了不同网格类型对所提出拓扑优化方法结果的影响，验证了其易于满足回转曲面加筋制造工艺要求、网格质量依赖性低等优势。然后分析了不同支反力约束值对拓扑优化结果的影响，以验证方法的适用性。

模型划分为六面体和四面体两种网格类型的拓扑优化结果分别如图12和图13所示。由图中可以看到，本文方法由于采用了各向异性过滤技术开展拓扑优化设计，优化结果表现出较低的网格质量依赖性，对于不同类型的有限元网格均能得到清晰、相似的加筋构型，且灰度单元较少，同时优化结果保证了筋条与蒙皮相互垂直，优化结果的拓扑特征经简单处理即可直接应用于工程中，满足回转曲面加筋制造工艺要求。

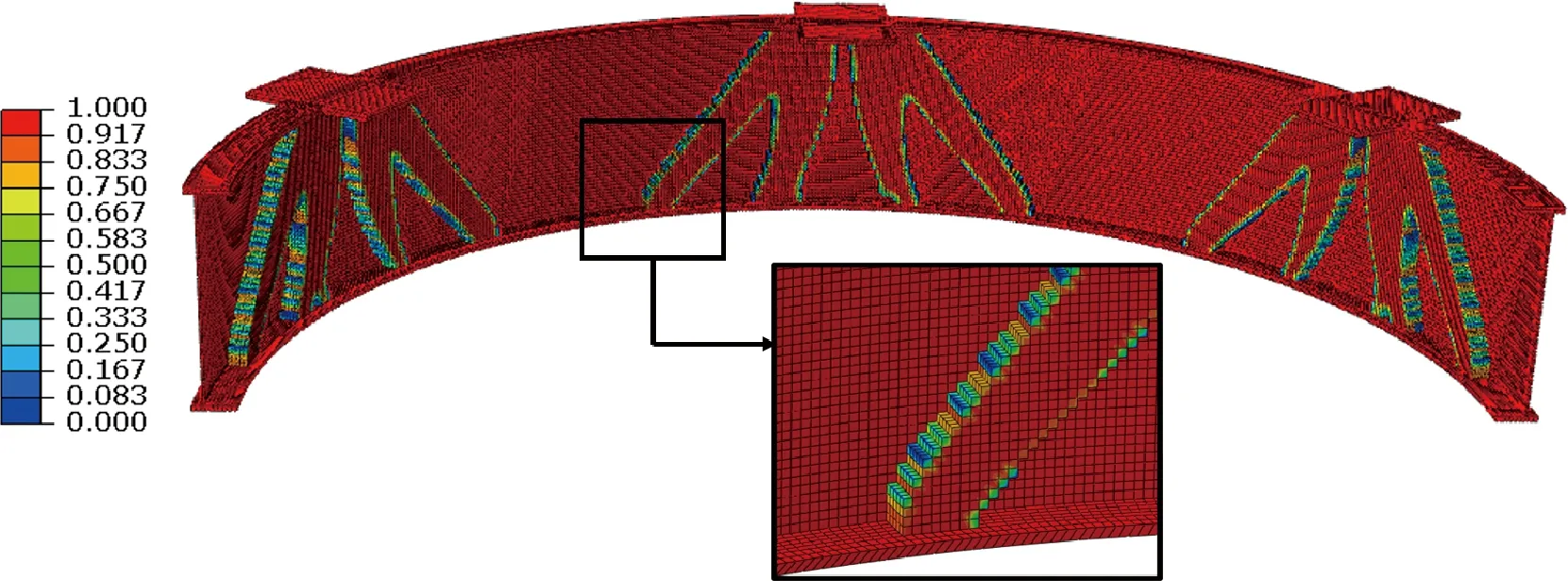
图12 拓扑优化结果(有限元模型划分为六面体网格，支反力约束为20 000 N)Fig.12 Topology optimization result (FE model is divided by hexahedral meshes, and constraint of reaction force is 20 000 N)

图13 拓扑优化结果(有限元模型划分为四面体网格，支反力约束为20 000 N)Fig.13 Topology optimization result (FE model is divided by tetrahedral meshes, and constraint of reaction force is 20 000 N)

图14为不同支反力约束下拓扑优化结果的构型图。由图可见，各优化结果的加筋构型基本相似，依然呈放射状。随着支反力约束值逐渐变小，约束条件愈发严格，导致中间的筋条逐渐变细，两边的筋条逐渐变粗，以使得集中力扩散地更加均匀。需要说明的是，论文中的对接环算例源于实际工程结构，其约束上限的选取是参考了实际设计需要的。本文提供的是通用设计方法，可以结合具体工程需求进行约束设置。

图14 不同支反力约束下的拓扑优化结果Fig.14 Topology optimization result with different constraints of reaction force

3.2 本文方法与传统放射肋结果对比分析

参考文献[2-3,9]中的放射肋结构形式，按照1.2节中图 4所示的建模过程，通过对平面形式的放射肋模型进行网格变形即可得到回转曲面形式的放射肋模型，结果如图 15所示。对模型进行集中力载荷下的静力学分析，参数设置与2.1节保持一致，放射肋结构的质量与2.3节中的优化结果保持一致，均为10.8 kg。得到应力结果如图 16所示，由图可知结构的最大应力为87.0 MPa，整体应力水平较低，结构的强度裕度较大。提取各支座支反力结果，列在表 1中。由表 1中可以看出，传统放射肋结构有5个支座的支反力大于20 000 N，尤其在集中力载荷附近的支座，即支座3、支座8和支座13附近的支座支反力较大，超出支座支反力约束，未能满足集中力扩散设计需求。传统放射肋设计方法与本文方法集中力扩散结果对比如图 17所示，为了进行扩散效果的定量对比，本文定义了集中力扩散率φ(0≤φ≤1)：

图15 传统放射肋结构有限元模型Fig.15 FE model of traditional radial rib structure

图17 本文方法与传统放射肋方法结果对比Fig.17 Comparison between results from proposed method and traditional radial rib method

(17)

式中：Fmax表示所有支座中的支反力最大值；F1和F2分别表示集中力完全没扩散(力都集中在一个支座)和完全均匀扩散(所有支座力相等)时所有支座支反力的最大值。可知对接环算例中F1=70 000 N,F2=14 000 N。基于式(17)可计算得到本文方法的集中力扩散效率φ1=89.6%，放射肋方法的扩散效率φ2=79.1%。本文方法的扩散效率比放射肋方法高10.5%，在集中力扩散能力方面具有明显的优势。

对比本文方法结果(图10(e))和传统放射肋结构(图15)的加筋构型可以发现，两种加筋构型均呈放射状，表明这类放射状的加筋构型具有较好的集中力扩散能力。传统放射肋结构传力路径较为单一，相比之下，采用本文方法可以得到更优的传力路径，能够高效地利用材料、避免质量冗余，因此具有更优集中力扩散效率。

3.3 网格变形方法应用范围及优势

上文对接环算例中的加筋回转曲面为柱面，形状较为规则，但实际工程中还存在大量变曲率回转曲面加筋的情况。如图18(a)所示，考虑回转体母线为曲率连续变化的任意曲线，其回转曲面模型如图18(b)所示。针对此类复杂结构，常规加筋建模方法繁琐、耗时且精度较低，同时也难以实现参数化。

基于1.2节中的网格变形方法可对图18中的变曲率回转曲面进行快速加筋特征提取及模型重构。如图19(a)和图19(b)所示，只需对背景网格域和目标网格域进行训练(算例中包含8280个有限元节点)，分别得到正向和逆向映射关系。如图19(c)和图19(d)所示，进行特征提取时，首先可基于正向映射关系将回转曲面展开为平面，在平面上可快速、便捷的人工建立加筋特征，进而基于逆向映射关系将平面加筋构型映射为回转曲面构型，且映射结果能保证筋条与蒙皮的垂直。

图18 变曲率回转曲面示意图Fig.18 Schematic diagram of variable-curvature shell of revolution

图19 变曲率回转曲面加筋壳网格变形示意图Fig.19 Schematic diagram of mesh deformation for variable-curvature stiffened shell of revolution

综上所述，本文提出的网格变形方法主要用于回转曲面加筋拓扑优化结果的特征重构，其主要有两方面的优势：首先，便于编程和软件制作，工程师每次只需向编译好的程序提供背景网格域和目标网格域，即可自动完成训练并得到映射关系；其次，代理模型可自动拟合回转曲面与平面的映射关系，无需过多关注曲面本身的特征，避免了繁琐的模型处理，将复杂的曲面问题转换为了简单的平面操作问题。

4 结 论

1) 提出了一种面向集中力扩散的回转曲面加筋拓扑优化方法。首先，建立了一种基于各向异性过滤的集中力扩散拓扑优化方法，可保证拓扑优化结果满足回转曲面加筋制造工艺要求。然后，提出了一种基于网格变形技术的拓扑优化结果模型智能重构方法，可以高效准确地重构回转曲面加筋拓扑优化结果。基于对接环算例开展研究，验证了所提出方法的适用性和有效性。

2) 讨论了不同网格类型与不同支反力约束对优化结果的影响，并与传统放射肋设计方法进行对比，验证了所提出方法具有集中力扩散效率高、满足回转曲面加筋制造工艺要求、网格质量依赖性低、拓扑特征重构高效等优点。同时给出了变曲率回转曲面加筋壳的算例，进一步说明了网格变形方法的适用性。

后续研究中，将面向更加复杂的工程结构形式和约束条件，进一步扩展所提出的拓扑优化和模型智能重构方法。