极小主义视域下的真谓词
高贝贝
紧缩真理论被看作是由具有相似观点的理论构成的集合,包含了一系列名称各异的真理论,主要有冗余论、代语句理论和极小主义理论,它们都认为真不是一个实质属性。对于“真的”是否是一个谓词这样一个问题,紧缩真理论内部是存有争议的。一般紧缩真理论认为“真的”在语句中不表达实质属性,无法充当语句的谓词。极小主义真理论作为紧缩真理论的一个特殊理论分支,主张真是归属于命题的弱属性([14],第153–159 页),“真的”相应地具有谓词的功能,只不过该谓词具有理论特殊性。
1 “真”与“真的”
“真”和“真的”是两个紧密联系的概念,“真”是“真的”的抽象名词化形式,“真的”则是对“真”的外在显式表达,“真”作为谓词是通过“真的”发挥作用的,有关“真”和“真的”意义理论的内容侧重点是不同的。按照极小主义真理论的主要代表人物霍维奇(P.Horwich)的观点,“极小主义真理论直接关注的是‘真的’这个谓词,而不是‘真’这个概念本身。它旨在明确对‘真的’意义起决定作用的非语义事实,并且此种非语义事实能够大致刻画出‘真的’在等值模式中所发挥的作用。”([6],第38 页)这也就是说,正是通过真谓词在等值模式中的具体使用,我们可以获得真谓词的意义,解释真概念所具有的性质。因为,“一般来说,除了等值模式所例示的以外,没有必要进一步探求一些关于真谓词更为深层次的事实,不需要任何其他的东西解释真谓词的具体使用。正是出于这种原因,我们能够得出结论:‘真的’的意义是由等值模式决定的。”([6],第38 页)在笔者看来,极小主义真理论侧重于“真的”意义的探究,这转变了一般真理论的研究范式,由原来直接研究“真”转向研究“真的”的意义,通过刻画“真的”的意义,间接地给出有关“真”的解释,运用真谓词(真的)在等值模式中的具体使用给出“真”所适用的外延(亦即那些为真的事实),真谓词所适用的外延在某种意义上体现了真概念的内涵,这就从外延的角度间接地定义了“真”,解释了“真”。
阿莫尔 伽布(B.Armour Garb)和贝尔(Jc Beall)指出:“有关概念K的理论旨在提供一个我们对Ck整体使用的最佳解释,其中Ck是表达概念K的语言表达式;相比之下,有关性质K的理论旨在提供一个关于K自身所有事实的最佳解释。一般来说,这两种说法之间会有很大的不同,前者目的在于解释相关语词的事实,而后者目的则在于解释这些语词所表达的东西或者语词所具有的意义。”([1],第85–96 页)依据阿莫尔 伽布和贝尔的观点,笔者认为,我们可以类推出如下结论:有关“真”的理论旨在提供一种能够解释真概念和真性质在具体语言表达式中表达的事实,即解释有关真的思想或陈述,而有关“真的”的理论则是旨在给出真所具有的意义,即“真的”在具体实例中的使用规则。前者在于解释“真”所表达的事实,而后者则在于解释“真”之意义。
具体来说,极小主义真理论有关真的公理源自于等值模式(〈P〉是真的当且仅当P,其中〈P〉是指命题P)的具体实例,对等值模式具体实例的接受构成了“真的”的意义。“真的”的意义不是通过提供其他具有相同意义的表达式确定的,也不是通过提供将每一个包含有真谓词的语句转换为等价于不包含真谓词语句的规则给出的,而是通过给定使用真谓词的基本规律或基本规则给出我们对所有使用“真的”具体实例的解释,从而获得“真的”的意义。
借鉴霍维奇区分外在性质和内在性质的理论,我们可以进一步明确“真”与“真的”。([14],第153–159 页)按照霍维奇的观点,外在性质是通过某种相应的具体非语义实体显现的,内在性质则是隐藏在具体非语义实体内部的,它是解释外在性质的基础。例如,“红色”作为外在性质,它能够通过苹果、玫瑰花等呈现出来,这样“红苹果”“红色玫瑰花”等就给出了“红色”的外延式解释,但是“红色”的内涵式解释则需要依赖内在的物理性质或化学性质。类似地,“真”属于内在深层次的东西,是对在特定意义下某人使用语词“真的”所需满足条件的刻画,属于语义层面的探讨。“真的”是对“真”这一语词现象所表达基本事实的描述,对真命题、真语句、真信念的分析。
真理论的主要论述是有关“真”的基本事实,这样一些基本事实能够用于解释其他与“真”相关的事实,例如指称和意义。而有关“真的”意义的理论是对语词“真的”基本使用情形的分析,“真的”的具体使用规则构成了其意义,“真的”的理论分析间接地解释了“真”。
2 作为语义谓词的“真的”
一般而言,谓词表达了对象的属性,诸如“白色的”“美丽的”等。然而,并非所有的谓词都是如此,“真的”就是一个特殊的谓词。在《思想:一种逻辑研究》中,弗雷格指出:“思想的性质,即真这种性质与事物的各种性质结合在一起。但是也要注意,‘我闻到紫罗兰香味’这个句子和‘我闻见紫罗兰香味,这是真的’这个句子确实有相同的内容。因此,我在这个思想上加上真这种性质,这似乎对这个思想没有添加任何东西。并非如此!研究者经过长期犹豫和辛勤的研究,最后可以说‘我过去猜测的是真的’,难道这不是巨大的成功吗?‘真’一词的意谓似乎是完全独特的。”([11],第133 页)
根据弗雷格的观点,“真的”是用于表达思想(或命题)的谓词,思想是语句的语义内容或者是所谓命题态度的对象。真能够作为一种性质与事物的各种其他性质结合在一起,但是真性质具有一定的特殊性,因为真谓词(真的)至少具有两种不同的使用类型([10],第230 页):
(I)〈P〉是真的。
(II) 我过去猜测的是真的。
在(I)中,〈P〉是指命题P,它表达了完整的语义内容。例如,命题“雪是白的是真的”和命题“雪是白的”表达了相同的内容,谓词“真的”作为一个逻辑谓词在此种形式中没有给命题增添任何新的内容,当断定雪是白的是真的时,我们只是把真作为一种特殊的性质归属于命题,事实上没有为命题表达的语义内容贡献任何新的东西。在(II)中,诸如“我过去猜测的”“亚里士多德所说的”等不同形式的语言表达式不是语义完整的命题,而是具有特定指称的名词短语。谓词“真的”作为一个谓词发挥着非常重要的作用,它确实给语句增添了相应的语义内容(作为命题表达语义内容的重要组成部分),是不能够简单地予以消除的。
实际上,无论是在(I)还是在(II)中,“真的”作为谓词都发挥着作用。从形式(I)来看,“真的”在其中主要起语法作用,利用该形式,“真的”在命题中所具有的逻辑推理作用得到极致的发挥。从形式(II)来看,“真的”是命题语义内容的重要组成部分,具有重要的语义作用。
从极小主义真理论的观点来看,“真的”作为谓词与一般谓词(例如“红的”“受重力作用的”等)具有极大的不同,真谓词具有理论特殊性:
第一,“真的”作为谓词是谓述命题的。“真的”谓述命题主要有如下两种形式:其一,“真的”是作为一个给定完整(语义完整的)命题的谓词,命题表达了一个完整的思想内容,“真的”对该命题没有增加任何其他的东西,此时允许把真看作是冗余的,这也就是弗雷格所主张的真谓词的使用类型(I)。其二,“真的”嵌入一个命题之中,此时的命题是不饱和的或者不完整的,“真的”是命题不可或缺的重要构成部分,这也就是真谓词使用类型(II)的形式表达。
第二,真谓词所表达的是一种特殊的逻辑性质。一般谓词将某种构成世界的实质属性归属于谓词所谓述的对象,然而真谓词却不具有此种功能。正如霍维奇所说,“‘真的’不能用于任何具体的对象,它不具有用于表达某种关系或实质属性的潜在本质。”([4],第2 页)当我们说“亚里士多德所说的是真的”时,我们并没有将任何实质性的属性,亦即那种作为世界组成部分的性质,归属于命题“亚里士多德所说的”。
这也就是说,“真的”没有将任何实质性的属性归属于一个命题或语句或信念。“真不是一种与某种特殊的感觉印象相符合的性质。它与我们以‘红的’‘苦的’‘散发丁香花味的’这些词指称的性质鲜明地区别开。”([11],第133 页)因为“命题与它的真之间的关系不同于雪和它的颜色(白色)之间的关系,而是类似于一个限定摹状词的涵义与其所描述的现实世界中的对象之间的关系。”([2],第141–162 页)这在一定程度上支持了极小主义的理论观点:真谓词所表达的性质不具有可感知性,不是通过感官感知的,而是一种特殊的逻辑性质。例如,当我们说出如下形式的语句:
(1)X是具有吸引力的。
我们将物理世界中“具有吸引力”这一性质归属于个体对象X。然而,当我们说
(2)X是真的。我们并没有把任何物理世界的属性归属于对象X(命题、语句、信念)。
从表面上来看,(1)和(2)共同具有形式
(3)X是F。
然而,“真的”这一性质完全不同于性质“具有吸引力的”,后者是一个物理性质,能够被具体的物理对象例示;前者则不然。真性质只是一个逻辑性质,是一个只具有逻辑推理作用的性质。正如在语句(2)中,通过“真的”的谓词作用,我们只能够推理得出X自身,除此之外没有任何其他的东西。通过如下的逻辑推理形式,我们能够明确真可以作为谓词且能够表达一种性质,发挥着不可忽视的逻辑推理作用。给定前提条件(2)和
(4)X=命题P。
可以得到
(5) 命题P是真的。所以
(6)P
从(2)到(6)的推理过程中,若真不表达任何性质,那么我们就不能够从前提(2)得到结论(6)。因此,当真作为谓词时,它必定表达了一种特殊的性质。
第三,真谓词具有特殊的逻辑推理功能。值得注意的是,虽然一般性谓词具有推理功能,但是其推理功能的发挥需要经验的验证,真谓词则不需要。([9],第59–61 页)真谓词不需要依赖于经验验证,而是凭借等值模式对其使用的限制而获得相应的意义,这是因为等值模式是先验的,不需要经过任何经验的验证。([12],第153–159 页)例如,我们从前提
(7)X是导电的。
可以推出结论
(8)X是金属。
从(7) 推出(8) 需要经验性的验证或实证性的观察,才能将导电和金属的特性联系起来。然而,“真的”作为谓词依赖于等值模式发挥推理作用,例如,给定前提(2)和
(9)X=雪是白的。
我们可以推出
(10) 雪是白的。
从前提(2) 和(9) 推出结论(10),我们依赖于等值模式具体实例的无穷合取,而不是具体的经验证实活动。
从极小主义真理论来看,“真的”作为谓词具有的特殊性源自于其是一个特殊的语义谓词。谓词“真的”不仅能够表达出某些表达式与相应表达对象之间的关系,而且能够表达出某些表达式的性质。塔斯基曾指出,真谓词具有理论特殊性,像“指称”“满足”等语义谓词,它们表达某种关系,即某些表达式和这些表达式所表达对象之间的关系,而真谓词却具有另外的一种逻辑特性,它表示某些表达式比如语句的一种性质。([13],第81–126 页)
何谓语义谓词?奎恩(W.Künne)明确给出了语义谓词的定义:“从广义的层面来说,一个谓词是语义谓词当且仅当它满足两个条件:一是该谓词要么表示一个表达式所拥有的性质,要么表示一个表达式与所表达的事物之间的关系,二是该谓词的意义依赖于表达式中构成部分的意义。比如,如果我们遵循斯特劳森对‘x谈论y’的使用,这里的谓词就不是一个语义谓词,因为它不符合条件一,它所表示的关系的左边是一个说话者,而不是一个表达式。再比如,‘x有5 个字母’不符合第二个条件,因为它不依赖于表达式中组成部分的意义。从狭义的层面来说,一个谓词是语义谓词当且仅当要么是它自身,要么是使用其他的一些谓词来定义它,这个用来定义它的谓词表示的是表达式与该表达式所描述的对象之间的一种关系。”([7],第179 页)
笔者认为,从广义语义谓词的角度来看,“真的”确实是一个语义谓词,首先,“真的”满足了条件一,其两种类型的使用分别对应了条件一中的要求,无论在(I)还是在(II)中,“真的”都表达了命题的一种特殊性质。其次,“真的”满足了条件二的要求,显然地,无论是在(I)还是在(II)中,“真的”在其中都发挥了重要的逻辑作用。当然,“真的”也有其特殊性,在(I)中,“真的”的意义依赖于整个命题在等值模式中的具体使用,在(II)中,“真的”作为命题的重要构成部分,整个命题意义的获得离不开“真的”,同样“真的”的意义也依赖于命题所具有的认知知识。
3 “真的”的意义
霍维奇曾明确指出,“真谓词的意义是由等值模式限定的,等值模式是先验的,具有解释性基础,有关它的解释不依赖于其他概念。”([5],第149–165 页)通过对霍维奇意义使用论([3],第105 页)的分析,我们以等值模式为理论基础分析“真的”的意义,有以下基本理论原则:
(i)“真的”的意义是一个概念或一种属性。从前文有关“真的”的理论分析,我们可知,“真的”作为一种特殊的谓词,它谓述了命题的某些东西,表达了一个属性概念,即“真的”的意义是一个谓述性的概念或是一种属性(用于表达命题的一种特殊属性)。
(ii)“真的”的所有使用源自它所具有的基础可接受性,这是“真的”具有解释作用的基础。“真的”的基础可接受性是由等值模式具体实例的可接受性构成的,等值模式的具体实例限定并解释了“真的”一词的具体使用。
(iii)“真的”的意义是由解释性的基础可接受性或使用属性决定的。我们通过“真的”的具体使用获得其意义,“真的”的意义是通过其在等值模式具体实例中的使用例示的,等值模式的具体实例是“真的”意义的外延性表达。
按照霍维奇的观点,“极小主义的主要理论是如下两个先验性论断的产物:第一,我们对等值模式具体实例的接受是真谓词所有使用的解释性基础;第二,任何一个语词的意义都是由解释该语词所有使用的基本事实产生的。”([5],第149–165页)霍维奇借鉴意义使用论的基本思想,简单地论证了“真的”的意义,并给出了一个概括性的理论解释。对霍维奇的这一观点,笔者表示赞同。为了更好地刻画“真的”的意义,笔者依据霍维奇的基本思想重新构造了如下论证过程,详细论证霍维奇意义使用论对于“真的”意义的理论构造:
(1) 任意一个语词的意义都是由其具有解释性的基础可接受性决定的。
(2)“真的”的意义是由其具有解释性的基础可接受性决定的。
(3)“真的”解释性的基础可接受性在于我们倾向于接受等值模式的具体实例。
(4) 等值模式在概念上是基础性的。
(5) 由(3)和(4)可知,“真的”的解释性基础可接受性具体体现在它在等值模式所有实例中的使用。
(6) 由(2)和(4)可知,“真的”的意义是由其在等值模式中的具体使用决定的。
可知,“真的”的意义是基于两个理论构建的并且这两个理论自身都是合理的:一是,“真的”所代表的事实是那些能够解释我们使用“真的”一词所表达的事实。二是,我们对于等值模式的接受解释了“真的”一词的使用。
为了更好地理解霍维奇有关“真的”意义的论证过程,我们接着详细分析整个论证过程所涉及的前提和结论。
(1)是对意义使用论基本理论原则的概括,意义使用论的基本思想是说,语词的意义是由其使用决定的,语词的使用规则是由其基础可接受性限定的,因此任意一个语词的意义都是由其具有解释性的基础可接受性决定的。(2) 则是将前提(1)表达的有关语词意义的普遍性理论推广运用于谓词“真的”。(3)是说我们倾向于接受等值模式的具体实例是解释“真的”所有使用情况的基础。正如霍维奇所说,“我们有关真谓词的所有使用是由等值模式的具体实例解释的。”([3],第105页)这就是说,我们对等值模式具体实例的接受是真谓词所有使用情况的理论基础,真谓词在等值模式中的使用发挥着重要的解释作用。例如,给定前提
(7) 柏拉图说雪是白的;
(8) 柏拉图说的是真的;
根据等值模式,我们可以推出
(9) 雪是白的。
在这样的推理过程中,我们不仅运用了莱布尼茨同一律,而且必须考虑相关的等值模式实例。更一般地说,我们可以得出这样的结论,除了我们对等值模式的倾向性接受以外,不需要其他关于真谓词深层次的事实,我们就能够解释真谓词的具体使用方式。
对于(4)来说,这里之所以强调等值模式的概念性基础,因为“真的”的基本使用规则决定其意义,而“真的”的意义则是我们倾向于接受等值模式的所有实例决定的。等值模式的概念性基础使我们解释“真的”的意义不需要依赖其他更深层次概念的理论基础,这样便能够避免还原解释产生的形而上学难题,亦即我们不需要依赖传统真理论解析真概念所遵循的形式规则:对于任意的x来说,若x是真的,那么就是说x具有某种特定的状态或特征。(5)则是(3)和(4)结合起来推理得到的理论结果,通过前提(3)和前提(4)的结合,“真的”的解释性基础可接受性转化为其在等值模式具体实例中的使用,将抽象性的概念转化为直观性的使用。
通过对霍维奇有关意义使用论基本思想的分析,笔者认为,“真的”的意义是由它的解释性基础可接受性或者它的使用属性决定的,其使用属性体现在我们倾向于接受等值模式的所有实例。霍维奇曾明确给出,“一个语词的意义属性是由该语词的某种特定的使用方式决定的。”([5],第141–162 页)语词的使用方式是语词的使用属性,语词的使用属性决定了与其相应的意义属性。实质上,语词的使用属性是一种内在属性,是一元的单一性的,它作为解释性的基础不需要依赖其他属性来解释。意义属性则具有关联性,它与其他非语义的概念具有密切联系,但是意义属性是由单一性的使用属性决定的。有关意义属性正确解释的逻辑形式不是

其中,X是指具体的语词,F指一个概念,f则是对F的具体表达形式,而R是一种非语义关系/cncomma 而是如下的逻辑形式
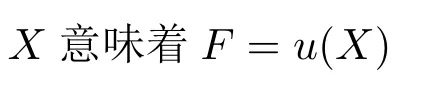
这里的使用属性u(X)被认为是非关联性的(non relational),它是基础性的,能够用于解释其他属性。([8],第85–87 页)
关于“真的”的意义理论在极小主义真理论的整个理论体系中居于重要的地位,它是真概念理论和真性质理论得以成立的理论基础,真概念以及真性质之所以具有某种特殊的逻辑功能得益于“真的”所具有的意义。“真的”的意义是其解释性的基础可接受性或使用属性决定的,亦即“真的”意义在于我们倾向于接受等值模式的所有可接受性实例,通过其在等值模式中的具体使用获得解释说明。“真的”的意义决定了我们对真的理解以及真在具体实例中所发挥的作用。我们理解“真”也就等同于我们知道谓词“真的”的意义。
总的来说,极小主义视域下的真谓词具有理论特殊性,作为谓词,“‘真的’没有把某种实质性的性质归属于某种实体,‘真的’所表达的性质不是现实世界的实体性质。事实上,真谓词的存在只是为了某种逻辑的需要,它能够满足我们忽略命题所表达的具体内容,而又期望接受某种命题态度的需要。”([4],第2 页)“真的”所具有的意义,使得真谓词虽然没有给语句增加任何的语义内容,但是它在具体的推理进程中发挥着不可忽视的逻辑作用。
——论胡好对逻辑谓词的误读

