弹弓论证与真之符合论

胡兰双

“弹弓论证”有很多种形式，不同的哲学家出于不同的目的使用它。该论证最早由丘奇（A.Church）提出（[4]，第29 页），用于反对卡尔纳普（R.Carnap）的意义实体。“弹弓”（slingshot）一词则是出自巴威斯（J.Barwise）和佩里（J.Perry），之所以叫它“弹弓论证”，是因为整个论证的篇幅很小，却是十分有力的武器，足以对很多重要的哲学观点进行攻击（[2]，第387 页）。

戴维森（D.Davidson）就曾用“弹弓论证”攻击过真理符合论，他的论证意在证明：并没有什么不同的事实供不同的真命题去与之符合，所有的真命题都符合同一个事实——那个唯一的“大事实”（the Great Fact）。这个结论不仅涉及到符合论中“事实”概念的合理性，还涉及到了符合论的一个重要的推论——关涉性原则。因此本文首先介绍真之符合论与“事实”以及“关涉性原则”之间的关系，并以此为背景，阐述并分析戴维森版本的“弹弓论证”，最后通过考量论证所使用的LP 规则和SP 规则，对它反符合论的有效性提出质疑。

1 真之符合论与“事实”

真之符合论的核心观点可总结为：一个真值承担者（truth bearer）为真，是因为它与“实在”（reality）相符合。从古典发展至今，符合论有很多版本，按照真值承担者所符合的“实在”类型的不同，库恩（W.Künne）将符合论分为“基于对象的符合论”（object based correspondence theory）和“基于事实的符合论”（fact based correspondence theory）。1可参见[8]，第三章。其中“基于事实的符合论”便是认为真值承担者所符合的“实在”是一种“事实”而非具体的“对象”。

这一观点在20 世纪初最具代表性，最初是由摩尔（G.E.Moore）将“事实”概念引入到符合论的定义当中。摩尔对于真、假的定义起初与亚里士多德的解释并无两样，他以“摩尔正在听管弦乐”这个信念2摩尔认为信念是真值承担者。为例，认为这个信念的“真”，是由“实际上摩尔正在听管弦乐来决定的”（[10]，第254 页）。而这个“实际上摩尔正在听管弦乐”被他称之为一个“事实”：“我们可以说，首先信念是假的，意味着宇宙中不存在信念为真时存在的那个东西。另一方面我们可以说，当信念为假时，宇宙中缺乏的那个东西和信念为真时呈现出来的那个东西是事实，它的本质是不会遭人误解的（unmistakable）。”（[10]，第256 页）

引入“事实”概念后，摩尔便用如下的方式定义了“真”：“说一个信念是真的，常常是说它所指称（refer to）的事实的确如此（is）或者已经存在着（has being）；说一个信念是假的，常常是说它所指称的事实并非（isn’t）这样或是不存在（has no being)。”（[10]，第256 页）

虽然摩尔对于“事实”概念进行了一定的解释，但更多的将其作为一种原初性的、基础性的概念，特别是摩尔将“命题”作为一类特殊的“事实”的做法让人不尽满意。

对比摩尔，罗素（B.Russell）对于“事实”与“命题”3罗素认为“命题”是真值承担者。之间的关系做了更为细致的说明，虽然他也认为“事实”是不能够被清晰定义的，但“事实”的确是使“命题”为真为假的东西（[13]，第6 页）。作为逻辑原子论者，罗素特别重视逻辑分析，认为分析的目的在于揭示出每一个命题与它所描绘的实在之间的关系。分析的途径包括：把复合命题分解为原子命题，把原子命题分解为名称和谓词等不可再分的终极单元。事实也是一样，原子事实是最简单的那类事实，可以分解为殊项和关系4这里将属性看作是一个一元关系。，一个原子事实仅包含一个关系。还有一般事实、存在事实以及否定事实这类特殊的事实。然后，专名对应殊项，谓词对应关系，原子命题对应原子事实，复合命题的真值可以化约为组成它的原子命题的真值，加上一些特殊的情况，罗素便将“真”刻画成了命题和事实之间的一种“同构”关系5以下对罗素真理论的总结大部分来自于[13]，也有一部分来源于[17]。：

一个命题X为真，当且仅当：

(I) 若X为原子命题，那么存在一个原子事实Y，使得X符合于Y;

一个原子命题X符合于原子事实Y当且仅当X与Y同构；

一个原子命题X与原子事实Y同构，当且仅当：

(i) 命题X中的n元谓词Rn意指6在罗素的原文中用的是“means”这个词，名词形式时用的是“meaning”这个词。按照常理，应该将“means”译为“意味着”，而不应该译为“意指”，但是由于罗素的意义理论是一个外在论，不同于我们一般理解的意义理论是一种内涵理论，考虑到这点，本文遵循《逻辑与知识》苑利均版本的译法，将其译为“意指”。但要提请读者注意的是，这一部分所使用的“意义”和“意指”二词，其实是同一个词的不同形态。事实Y中的n元关系Rn；

命题X中的n个名称a1,···,an意指事实Y中的n个殊相a1,···,an。

(ii) 命题X中的位置元素O 等同于事实Y中的位置元素O。

(II) 若X为否定命题、全称命题或存在命题，那么分别存在否定事实、一般事实、存在事实Y，使得X与Y相符合。

(III) 若X为分子命题，则：

(i) 若X为p ∧q的形式，则存在原子事实p′和q′使得，p与p′相符合，q与q′相符合；

(ii) 若X为p ∨q的形式，则至少存在一个原子事实p′或q′，使得p与p′相符合或q与q′相符合；

(iii) 若X为p →q的形式，则存在原子事实q′使得q与q′相符合，或存在否定事实¬p′使得p为假。

(IV) 若X为逻辑命题，则X的真是先验的。

罗素的符合论被认为是符合论的代表性理论，“真值承担者为真是因为其与事实相符合”便一度成为了符合论的代表性观点，在二十世纪初期与真理融贯论、实用主义真理论展开了激烈的论战。

这里要注意，有一类真理被认为是符合论鞭长莫及的，那就是逻辑数学真理。罗素认为这类命题的“真”是先验的，逻辑经验主义者更是主张对“真”进行分类，分为“分析的”和“综合的”，分析命题靠其形式先验为真，而综合命题则需要依靠经验事实为真为假。这也演变出了后来所有传统真理一元论所面临的困境——“领域问题”（the Scope Problem）7这种称谓可参见[15]和[9]。，即“真”在不同的话语领域下是否有不同的构成。本文无意讨论这个问题的解决方案，只是提醒读者注意，后文对于“弹弓论证”的分析中，会涉及到这个问题。

2 真之符合论与“关涉性原则”

符合论还必须遵循一个推论，这里称之为“符合论的关涉性原则”（Aboutness principle of correspondence）：若一个命题（或语句）为真，那么这个命题（或语句）与相符合的实在之间必须具有密切相关性。（[11]，第28 页）

这个直觉是可以从不同阶段符合论对于“符合关系”的刻画中得到。在摩尔的符合论中，一个信念为真，必须是它所“指称”的事实存在或的确如此，只有这样，真信念和事实之间才能构成“符合关系”。摩尔通过对信念的分析，确立了命题与事实之间的“指称关系”。他认为信念分为“信念的行为”（the act of belief）和“信念的对象”（the object of belief），“信念的行为”在每个信念中都相同，而“信念的对象”则各有不同，这个信念的对象就是“命题”（[10]，第258–259 页）。摩尔将命题视为一种事实，视为宇宙中一种真实存在的东西（[10]，第260 页）。因此，无论信念真、假，它们都对应着一个命题事实。但命题也有真值，是它所具有的、基础的、不可分析的属性。信念的“真”是由命题的“真”来决定的（[10]，第262 页）。他进一步用“命题之真”来解释信念与事实之间的指称关系：一个信念所“指称”的事实，便是信念的对象为“真”时的那个事实，是“与那个信念有关系的事实，而非其它事实”（[10]，第262 页）。虽然摩尔对于命题的定位、对于命题“真”的解释十分容易让人产生质疑，但是他却凭借信念的对象，确立了“信念”与相符合的“事实”之间的相关性：不同的真信念，信念的对象是不同的，因而不能符合相同的事实。罗素的理论更加体现了这一点，原子命题仅仅与其内部结构有一一对应关系的原子事实相符合：必须找到名称所指称的个体，谓词所指称的关系所组成的事实。因此，符号的“意指”关系，在确立真命题与所符合的事实之间的相干性上起到了关键的作用。可以看出，导致“相关性”的要素，都包含在“符合关系”的定义当中，因此，符合论中对于关涉性条件的需求其实可以看做是“符合关系”的一种推论。“弹弓论证”之所以被认为是一种反符合论的论证，正是因为它的结论违背了符合论所主张的“关涉性原则”。

这里要提请读者注意两点：第一，如果说“关涉性原则”是“符合关系”的推论，那么随着不同版本符合论对于“符合关系”定义的不同，其对于“关涉性原则”的要求程度是不同的。例如摩尔的符合论则是完全要求真信念与特定事实之间的“符合关系”是一种一一对应关系，因为信念不同，信念的对象也是不同的，这种符合关系对于相干性的要求最高。而罗素的同构符合论看似做了更为细致的要求，但是以符号的“意指”关系做为相干性的决定性因素，不禁会让人想到“共所指”“共外延”的情况，这使得两个不同的命题符合于同一个事实的情况成为可能，下文我们便可以看到，“弹弓论证”所使用的两个重要原则便是在这方面做了文章。若将阿姆斯特朗（D.M.Amstrong）的“使真者理论”看作是符合论的一种当代变种理论，那么“使真关系”便是一种弱化了的“符合关系”，允许多对多关系的成立，但这并不意味着“关涉性原则”所要求的，关系双方的“相干性”对于“使真关系”来讲是不必要的，相反正是由于“使真关系”对于“相关性”要求的弱化，才导致了“不相干的使真者”系列论证对使真者理论的质疑8“不相干的使真者”问题分为三个论证，第一个是必然真命题的广泛随附性问题，第二个是使真者不足道的问题，第三个是使真者一元主义。详细请参见[12]，第959–970 页。。所以，无论何种版本的“符合关系”，关涉性原则所要求的关系双方之间的“相关性”都是必要的，只是程度有所差别。第二，关涉性原则里的“密切相关”是一个相对模糊的概念，本文仅将其程度限定在否定可识别的基础之上，因为实际上我们总是能够就什么情况下这种相关性是丧失的达成一定的共识，目前将这个原则限定在这种程度之上便足够了。

3 戴维森的“弹弓论证”

戴维森在他的很多著作中都提及过“弹弓论证”。早在1967 年的文章中，他用弹弓论证来表明：所有的真句子指称（refer to）同一实体（same entity）（[6]，第314 页）。随着他反符合论的观点逐渐明确，在后期的著作中，他将这个结论的说法修改成：“所有的真句子符合（correspond to）相同的事实，并且是唯一的大事实（the Great Fact）”（[5]，第42 页）。这里要考察的便是他后期的版本，该版本的论证依赖于如下两个规则：

• 逻辑规则（LP）：

如果〈φ〉↔〈ψ〉，那么[φ]fact=[ψ]fact。

即任意两个逻辑等值的命题符合相同的事实。

• 语义规则（SP）：

如果〈φ〉 ⇐⇒〈ψ〉，那么[φ]fact=[ψ]fact。

即任意两个语义等值的命题符合相同的事实。

这里的语义等值的概念需要进一步说明：

• 语义等值：

〈φ〉 ⇐⇒〈ψ〉当且仅当：

(I)a和b是两个具有共指（co reference）的单称词项（singular term）；

(II)〈φ(a/b)〉=〈ψ〉。

即两个命题是语义等值的，当且仅当它们的不同之处仅在于一个命题中的单称词项被另一个命题中的具有相同所指的单称词项所代替。

我们可以用如下三个命题解释这两个规则：

(1)〈北京在石家庄的北方〉

(2)〈石家庄在北京的南方〉

(3)〈石家庄在中国首都的南方〉

首先看命题(1)和(2)，按照戴维森的观点，它们是两个逻辑等值的命题，根据LP 规则，它们符合相同的事实。再看(2)和(3)两个命题的不同之处仅在于(2)中的“北京”被(3)中的“中国首都”所替换，但两个词项是共外延的，因而根据SP 规则，它们符合相同的事实。若这两个规则是合理的，那么这三个命题符合相同的事实。单看这三个命题，它们似乎在说同一件事——两个城市的方位关系，并且它们都是真命题，因而它们应该符合相同的事实。

令〈φ〉和〈ψ〉是两个任意的真命题，o是任意的对象的名称，则“弹弓论证”便可表示如下：

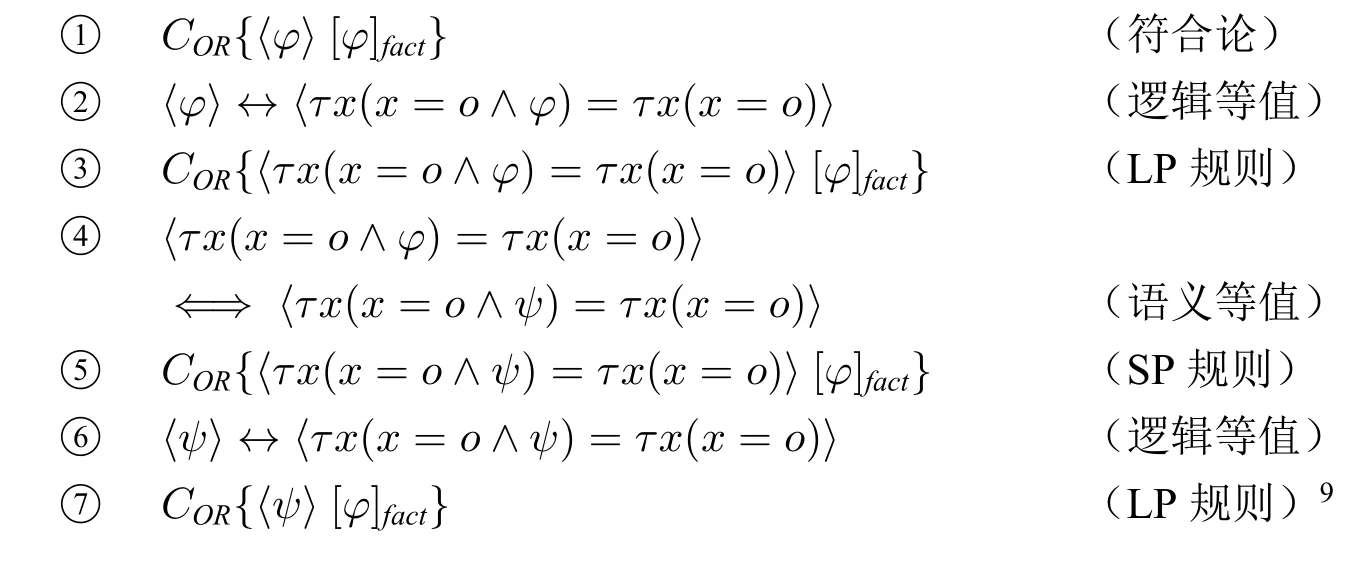
9文献[16]也列举了戴维森版本的“弹弓论证”，不过是将规则应用于“事实”一方，而不在“命题”一方，笔者认为，给出应用于“命题”一方的论证更为合理且更便于理解。

下面对这个论证进行解释：

根据SP 规则，〈τx(x=o ∧φ)=τx(x=o)〉和〈τx(x=o ∧ψ)=τx(x=o)〉符合相同的事实，由可知〈τx(x=o ∧φ)=τx(x=o)〉符合[φ]fact，因此〈τx(x=o ∧ψ)=τx(x=o)〉符合同样的事实，成立。

因此，戴维森用“弹弓论证”意在证明，任意两个真命题都符合相同的事实，进而推出所有的真命题都符合唯一的大事实，这无疑是违反符合论的“关涉性原则”的。进一步说，这样的结论如若成立，那么符合论的核心概念“符合关系”中的相干性刻画是缺失的，这会使得“符合关系”本身变得不足道，进而使得“符合论”做为真理论的合理性受到质疑。

我们可以看出戴维森的“弹弓论证”十分依赖逻辑规则和语义规则，这两个规则成立与否又涉及到指称理论、摹状词理论等诸多问题，因此，若想考察“弹弓论证”的有效性，就要从这两个规则的分析入手。

4 对LP 规则的考察

接受逻辑规则的直觉如下：命题是对世界的描述，如果两个命题的真值总是相同，说明它们所描述的东西也应该是相同的，进而它们所符合的事实也相同。因此，两个逻辑等值的命题符合相同的事实。但是，若要使得“弹弓论证”有反符合论的作用，那么它所使用的前提必须与符合论的观点不相冲突，若一开始，论证就建立在与符合论相悖的前提上，那么根本达不到反符合论的目的。这里就要探讨一下，能与符合论相适用的“逻辑等值”的标准到底是什么？看以下几组命题：

组1 的两个命题被看作是逻辑等值的，保障它们能构建双条件句的规则为：如果a在b的北方，那么b在a的南方，反之亦然。就其本身的表述而言，两个命题都涉及相同的对象——北京和石家庄两座城市，不同之处在于使用了“南”“北”两个不同的方位表达方式。虽然，无论从命题逻辑的角度将二者抽象化为p和q，还是从谓词逻辑的角度上将二者形式化为Nab和Sba，单从语形以及逻辑规律的方面考虑，二者都没有任何相互推演的能力，说其是逻辑等值略显牵强。但加上物理规律——Nxy ↔Syx的保障，说这两个命题符合相同的事实也不无道理。按照传统符合论的事实观来说，大多数符合论者会承认在这种类型的逻辑等值命题之间，LP 规则是有效的。

组2 的两个命题的逻辑等值依赖于逻辑中双重否定规则的保障：p ↔¬¬p，而这条规则的成立在语义上依赖于对逻辑常项“¬”的解释。命题p和¬¬p是逻辑等值的，但是它们是否符合相同的事实就不像组1 那么容易确认了。首先，无论在哪种符合论的观点之下，说〈北京在石家庄以北〉这个命题符合于[北京在石家庄以北]fact这个事实是没有问题的，但是〈并非并非北京在石家庄以北〉这个命题是否也符合于同一个事实是有争议的，要看如何分析这个命题，若将其看成是如下形式：〈¬q〉（其中q=¬p），那么应按照罗素的理论，该命题应该与一个否定事实相符合；按照使真者理论，该命题使真者应该包含一个二阶总事态11这所说的是阿姆斯特朗关于否定命题使真者的表述，详细可参见[1]。，因此它不可能与总是与原肯定命题符合相同的事实。其次，面对这种双重否定的模式，罗素也表明过，我们首先要处理的是句子的形式，而不是处理事实的形式，因此根据逻辑常项“¬”的解释，将〈¬¬p〉的真值问题归结到〈p〉这个命题上也符合逻辑原子论者的一贯作风。但要注意，这一切都要建立在对于“¬”这个常项的解释以及p ↔¬¬p成立之上。但这个规则总是成立吗？在直觉主义逻辑中，根本没有p ↔¬¬p这条规则，因而两个命题都不是逻辑等值的，二者真值并不总是相同的。最后，符合论的核心观点便是：不是我们语言中的东西，也不是我们思维中的东西，而是外部世界中的东西使得一个命题为真或为假。因此，既然对于“否定”的解释在某种程度上决定了该命题的真值，那么按照符合论的核心观点，它就应该对应着外部世界中的某样东西12吉拉·谢尔（G.Sher）的实质性真理论便是做了这方面的工作，详细请参见[14]。，这个观点适用于追问所有包含逻辑连结词的命题，若果真如此，后一命题比前一命题在世界中对应着更多的东西，即使它们的真值总是相同，它们所符合的事实也是不同的。总之，LP 规则在这类逻辑等值命题上是否有效是存在争议的。

再看组3，前两组等值的两个命题在表述内容上都有相关性，但这组逻辑等值命题不同，后一个命题比前一个描述了更多的内容。从真值上看，它们的确是等值的，等值式的构造基于两个背景条件：其一是罗素这个对象具有同一性使得命题〈罗素是罗素〉这个命题为永真式，其二是我们对于合取命题真值的解读方式。当然“合取”也是逻辑联结词的一种，这里不再讨论逻辑联结词对于真值的影响，只看在符合论的观点下，它们是否真的符合相同的事实。若二者符合相同的事实，那么〈罗素是罗素〉就不应该对应任何事物，这就涉及到符合论者对于〈罗素是罗素〉这个命题如何理解的问题。与〈北京在石家庄以北〉命题不同，它们凭借自身的形式为真，无需经验内容。若我们将这类分析命题的真值判定排斥在符合论能解释的范围之外，如维特根斯坦那样认为“重言式并不是世界的图式”，抑或是像逻辑经验主义者那样将“真”进行分类，符合论的应用范围就缩减了，并不涉及对分析命题成真方式的解释，那么LP 规则在这类等值命题中的运用是不合理的，原因在于：若命题包含了分析真命题作为组成部分，那么包含分析命题的那部分，我们就无法用符合论的方法验证它是否符合某一事实，因此这个包含分析真命题的命题本身包含两种成真方式，并不能简单地说它符合怎样的事实。也就是说〈罗素是罗素并且北京在石家庄以北〉这个命题不符合任何事实，那种将整个命题看作是符合事实的，又将命题的一部分看作不用符合事实的做法，本身就是一种秉持双重标准的做法。另一方面，如果符合论者不承认这种划分，坚持真理一元论，认为无论什么命题，它的“真”都是由世界决定的，那么，两个命题也并不符合相同的事实，LP 规则是不成立的。因此，在这类逻辑等值命题之间，LP 规则要么使用是不合理的，要么是不成立的。因而LP 规则最好避免对含有分析命题的逻辑等值命题的讨论，只讨论那些描述具体事物的偶然命题。

为此，拉斯穆森（J.L.Rasmussen）提出了一个“限制版弹弓论证”（[11]，第179页），认为只要将前提改为“任意两个描述具体事物的偶然真命题〈φ〉和〈ψ〉”即可，其余条件不变，得出的结论是“任意两个符合描述具体事物的偶然真命题符合相同的事实”，仍然对符合论造成威胁。但是，这种改造并没有解决实质问题，因为即使〈φ〉是描述具体事物的命题，与其逻辑等值的命题〈τx(x=o∧φ)=τx(x=o)〉是否与〈φ〉一样描述相同的内容也是不一定的，这一点我们可以通过组4 看出。

组4 的两个命题就是戴维森版本的“弹弓论证”逻辑规则的实例化。与组3 不同，组4 的两个命题的确都是关于具体事物的偶然命题，且从真值上看，两个命题的确逻辑等值。但它们真的符合同一个事实吗？很明显〈北京在石家庄以北〉这个命题是表达北京和石家庄这两个城市的方位关系，而〈那个特定唯一的x（x是罗素并且北京在石家庄以北）等同于那个特定唯一的x（x是罗素）〉这个命题主要表达的是两个被限定摹状词所指称的对象具有同一性。二者的表述并无直接关联，若它们都为真命题，那么根据符合论关涉性条件，它们所符合的事实必然不同。塞尔也表示过相同的观点，他认为在这两个命题中，罗素和他的同一性与〈北京在石家庄以北〉这个命题没有任何关系，它们并不应该符合相同的事实（[18]，第188–189页）。巴威斯和佩里也认为，命题所符合的事实应该是与命题的主题相关，因而前一个命题与罗素无关，后一个命题与罗素有关，二者不可能符合相同的事实（[3]，第24–25 页）。其实这一点也可归结为和组3 相同的解释中去，罗素这个对象的同一性在决定命题的真值上发挥了很大的作用，符合论不能忽略这个因素的存在，若强行认为LP 规则对于这样的等值式是成立的，本身就违背了符合论的“关涉性原则”，使得整个论证从根本上建立在一个违背符合论的前提之上，自然会得出与符合论相悖的结论。

总之，要使LP 规则能无争议地与符合论相适用，那么它最好是被应用于如组1 那样的——不包含逻辑词汇、分析命题、数学命题、抽象实体、描述具体事物的——偶然命题上，且两个逻辑等值命题之间必须十分相关。我们很难看出“弹弓论证”所使用的逻辑等值规则能符合如上要求。另一方面，面对四组逻辑等值命题与LP 规则之间的匹配所产生的矛盾，符合论者必须回答一个核心问题，那就是符合论是否承认领域问题？即是否承认在不同的话语领域下，句子的“真”的构成方式有所不同？若承认领域问题，那么，符合论仅仅只能应用于某个特定的话语领域，不能用于解释包含逻辑命题、数学命题等命题的真值。若不承认领域问题，那么符合论就要相继解释逻辑、数学、抽象命题到底在世界中扮演着怎样的角色，这又涉及到实在论的立场。对此，李主斌也在他的文章中表示过：“弹弓论证所基于的表面看来毫无问题的SS 原则（就是本文中的LP 规则）13括号内注释由笔者所加。实际上依赖一个非常有争议的论题。”（[16]，第42 页）要使符合论免受类似的攻击，就要使理论更加全面和完善。14其实，有很多版本的弹弓论证是不依赖于LP 规则的，但是都会依赖于其它前提，例如哥德尔（K.Gödel）版本的“弹弓论证”依赖于他所提出的（GI）原则，但是这些前提也是有问题的，详细可参见文献[16]第42–43 页。

5 对SP 规则的考察

语义规则是说，两个语义等值的命题符合相同的事实。“弹弓论证”的支持者认为这个前提是可接受的，原因在于命题所符合的事实就是关于命题所描述的对象的实际情况，那么既然替换部分所指称的对象没变，那么事实的构成也就没发生变化，两个命题符合相同的事实。

但很快有人会提出如下反对意见：

这两个命题的唯一区别就是后一命题中的“马冬梅”换成了“那个住在楼上302房间的人”。但是它们显然不符合同样的事实，因为夏洛知道马冬梅具有同一性并不意味着他知道马冬梅的家庭住址。因此语义规则的适用范围被限定在不包含非外延性词汇（如相信、知道、渴望等）的语境当中。

接下来看一组不含非外延性词汇的命题：

在这两个命题中，“柏拉图的学生”和“《形而上学》一书的作者”进行了替换，并且它们实际上是共所指的，其余的部分保持不变。那么它们是两个语义等值的命题，根据SP 规则，它们应该符合相同的事实。但很明显它们分别赋予了“亚里士多德”这个对象不同的属性，不可能符合相同的事实，因此SP 规则并不总是有效的。

其实这种替换问题也可以类比到罗素的摹状词理论中关于同一性问题的例子当中：“司各脱是司各脱”和“威弗利的作者是司各脱”这两个命题中，“司各脱”和“威弗利的作者”所指相同，因而二者语义等值。但是前者是重言式，无需经验内容，而后者必须依赖经验内容，替换后的两个命题并不符合相同的事实，仍然说明SP 规则并不总是有效的。

当然，对这类命题的分析方法与摹状词理论有很大的关系。按照罗素的摹状词理论，限定摹状词并不是单称词项，不具有指称意义，因此“弹弓论证”中的摹状词“τx(x=o ∧φ)”和“τx(x=o ∧ψ)”根本不是单称词项，SP 规则在“弹弓论证”中的使用是不恰当的。当然也有摹状词理论认为摹状词是具有指称意义的，例如唐奈兰（K.Donnella）的观点，他区分了摹状词的两种不同的使用方式：归属性使用（attributive use）和指称性使用（referential use）。15详细可参见[7]。当一个摹状词被归属性使用时，主要目的是将一些属性归属给适合该摹状词的对象；而指称性使用的目的则是在于指出所谈论的对象是哪一个。那么，按照SP 规则要求，只有在指称用法的时候，摹状词才能相互替换。接下来看“弹弓论证”中用于替换的摹状词，“τx(x=o ∧φ)”和“τx(x=o ∧ψ)”，它们都可以被认为是一种描述性用法，前两个摹状词把“使命题φ或ψ为‘真’”的属性赋予对象[o]fact，在使用这组摹状词的时候，重点不在于它所谈及的那个对象，而在于在什么样的条件下，它才是那个对象。因此，两组摹状词都是描述性使用，不符合SP 规则的替换要求。

有人可能反对上面将两个摹状词理解为描述性用法，而认为它们是指称性用法，理解为表述在特定条件下的那个对象。接下来要讨论的是，即便强行认为“弹弓论证”中的摹状词具有指称功能，它们也不必然共所指，看下面的例子：

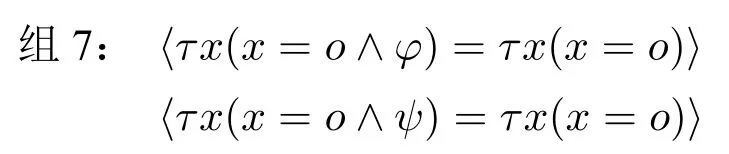
τx(x=o ∧φ)和τx(x=o ∧ψ)这两个摹状词指称相同，都指向[o]fact。我们知道，限定摹状词的指称取决于它的表意，两个限定摹状词是否指称同一个对象，取决于它们的表意是否总能让我们准确无误地找到那个对象。但是我们看τx(x=o∧φ)，〈φ〉并没有把什么东西归属给对象o，因为它是任意的真命题，这种表达方法令人疑惑。

为了解释〈φ〉和〈ψ〉在限定摹状词中所起的作用，有人将它解释为“那个特定唯一的x，假定（provided）φ时x是o”；或“那个特定唯一的x，仅当（only if）φ为真时x是o”，我们这里仅分析拉斯穆森所给出的一种解释，将其解释为“在这样的一个宇宙中”（is in a universe in which…）（[11]，第182–183 页）。那么组7 就变成了：

先不论两个句子是否依然语义等值，就连表达式本身所表达的同一关系都很难保障。一旦引入“宇宙”这个条件做约束，“那个在φ为真的宇宙中的o”和“o本身”是否同一不能确定。因此，这两个命题很难说与〈φ〉和〈ψ〉有逻辑等值关系，LP 规则在这里首先就是使用不当的。

其次，若我们将那个“x=o,andφis true”这样的“宇宙”记为U1，将“x=o,andψis true”这样的宇宙记为U2，那么，原来的两个摹状词就变为了“τxthatxis inU1”和“τxthatxis inU2”，除非能证明U1和U2总能是同一个宇宙，否则二者显然不能总是算作共指的。

因此，虽然“那个在〈φ〉为真的宇宙中的o”和“那个在〈ψ〉为真的宇宙中的o”都指向“o”，但是由于限定性条件的变化，个体的同一性不能被保障，二者并不必然共指，两个命题不能算作是语义等值的。同理，若引入“宇宙”这样的概念，“北京”和“中国的首都”也不必然共指。因此，即使SP 规则是正确的，“弹弓论证”也无法满足其共指的使用条件。

以上说法可能遭到如下质疑：

若规定〈φ〉和〈ψ〉存在于同一个宇宙中，那么U1和U2是同一个宇宙，这样就可以达到共指的要求了。

对此可以进行如下回应：既然引入了“宇宙”这样的概念，那么仅有两种情况能保障U1和U2总为同一个宇宙。首先，〈φ〉和〈ψ〉总是同一个命题，这一要求显然达不到，“弹弓论证”的主要前提就是〈φ〉和〈ψ〉是任意不同的真命题，若只是证明相同的命题总是符合相同的事实，并不会使得“弹弓论证”达到反符合论的目的。其次，只有〈φ〉和〈ψ〉都是必然真命题时，才能保证二者为真所在的宇宙可能是同一个宇宙。但我们前面对LP 规则的分析可知，两个命题都被限定在表达具体事物的偶然真命题上，因此它们也达不到这样的要求。

若放弃拉斯穆森的改写方法，摹状词中的命题仅仅是表达一种限定条件，两组摹状词只是对同一个对象的不同称呼,那么，这又回到了最初的那个问题，既然〈φ〉和〈ψ〉对对象[o]fact没有任何谓述作用，它们又不标记一个“宇宙”或“可能世界”，那么它们为什么能影响摹状词的指称，何以成为对同一个对象的不同称呼？有人仍可能质疑道，语言是有意向性的，我们可以有意将一个命题的真值同一个对象联结起来，或者就这样强行规定。若是这样，就要看所涉及的对象是否是人为可定义的了。一个纯客观对象[o]fact，我们又如何有意的将一个与其不相干命题的真值，强行加注到这个对象的身上呢？

退一步承认这种摹状词构成的合理性，能够达到共指替换的要求，那么替换后的两个命题的确符合相同的事实吗？仍然看组7，在前面讨论LP 规则时曾说过，影响这组命题的真值的不仅是〈φ〉和〈ψ〉两个命题的真假，还有对象[o]fact的同一性。有趣的是，“弹弓论证”中在强调逻辑等值命题符合相同的事实时，注重的是[φ]fact和[ψ]fact对逻辑等值的命题真值的作用，而强调语义等值命题符合相同的事实时，则是注重它们都表达了对象[o]fact的同一性，这里出现了对〈τx(x=o ∧φ)=τx(x=o)〉这个命题真值要素的不同侧重，其实两种说法都是不全面的。

6 总结

戴维森版本的“弹弓论证”试图证明所有的真命题都符合同一个“大事实”，这个结论虽然在一定程度上并没有偏离符合论的立场，认为真值承担者为“真”的原因在于外部世界，却违背了符合论的一个重要推论——关涉性原则，即一个真命题要与其符合的事实之间有密切的相关性。符合论对这种“相关性”的要求源于各个版本的符合论对于“符合关系”的刻画之中，例如摩尔的“指称”关系刻画下的“一一对应”关系，以及逻辑原子论者所主张的命题与事实之间的“同构”关系等。若任意的真命题都能与相同的“事实”构成“符合关系”，那么意味着“符合关系”中的相干性刻画是缺失的，这会使得“符合关系”本身缺乏存在意义，变得不足道，而无论哪个版本的符合论，“符合关系”的刻画都是核心任务，因此“符合关系”的不足道就会导致“符合论”本身的无意义，因此若“弹弓论证”是成立的，那么的确可以达到反符合论的目的。

戴维森版本的“弹弓论证”十分依赖于逻辑规则和语义规则的使用，即LP 规则和SP 规则。通过分别考察这两个规则在“弹弓论证”中的使用，我们发现要使LP 规则能无争议地与符合论相适用，那么它最好是被应用于不包含逻辑词汇、分析命题、数学命题、抽象实体、描述具体事物的偶然命题上，且两个逻辑等值命题之间必须十分相关。我们很难看出“弹弓论证”所使用的逻辑等值规则能符合如上要求。另外，“弹弓论证”中所构造的摹状词能否算得上单称词项是有争议的，即便是它们都有指称功能，由于它们的“奇特”构造也很难达到SP 规则的“共指”要求。综上所述，无论是SP 规则还是LP 规则，在“弹弓论证”中的使用，都是错用或无效的，因而“弹弓论证”不能达到反符合论的目的。但是通过对“弹弓论证”的分析，却可以引申出一系列符合论的背景理论的探讨，例如实在论立场、事实概念的同一性问题、领域问题、指称理论等，符合论要发展完善，仍需对这些问题加以回应。