基于PCA算法的人脸识别技术研究
郭磊 周文杰 高少伟


摘 要:身处信息时代,为了保护信息安全,如何准确鉴定某个人的身份,已经成为社会各界的难点。作为生物识别技术的一个重要分支,人脸识别技术在商业、安全、身份认证等领域有着广泛的应用。通过对传统PCA、分块PCA、MPCA以及二维PCA的人脸识别算法中的特征抽取方法以及对算法取不同参数情况下的性能和算法间性能对比,得出二维PCA性能更优的结论,并以此为基础,通过软件工具设计出了基于以上四种方法的人脸识别技术的仿真系统。
关键词:人脸识别;特征抽取;主成分分析
中图分类号:TP311.52 文献标识码:A 文章编号:2096-4706(2021)05-0108-06
Research of the Face Recognition Technology Based on PCA Algorithm
GUO Lei,ZHOU Wenjie,GAO Shaowei
(College of Electronic and Information Engineering,Guangdong Ocean University,Zhanjiang 524088,China)
Abstract:In the information age,in order to protect information security,how to accurately identify a persons identity,has become a difficult point for all walks of life. As an important branch of bioidentification technology,face recognition technology has a wide range of applications in business,security,identity authentication and other fields. Based on the traditional PCA,block of PCA and MPCA and two-dimensional PCA face recognition algorithm of feature extraction method and the algorithm performance under different parameters and performance comparison between algorithms,two-dimensional PCA performance better conclusions,and on this basis,through the software tools to design the face recognition technique based on the above four methods of simulation system.
Keywords:face recognition;feature extraction;PCA
0 引 言
生物特征技术是指利用人体固有的、具有稳定性和唯一性的生理特征,如指纹、面部、虹膜等来进行身份鉴定的技术。作为生物特征识别的一个重要方面,人脸识别技术在嫌疑人的身份识别、互联网的认证口令以及银行系统的身份验证等各领域有着广阔的应用前景[1]。同时,人脸识别技术还和其他领域存在交集,如神经网络、人工智能、心理学等。
目前,人脸识别研究的主流方向已经基本确定,有基于主成分分析方法(PCA),基于Fisher线性判别分析方法(LDA)以及局部特征分析方法(LFA)等。除了对静态的人脸图像进行识别,动态人脸识别以及三维图像研究也逐渐成为研究重点[2]。本文主要对PCA及其改进的算法进行研究,再通过软件工具实现人脸识别的仿真系统,并对算法性能进行比较。
1 基于传统PCA的人脸识别算法
基于传统PCA的人脸识别算法的主要思想就是在原始的人脸空间中求出一组正交向量,然后利用PCA方法保留其中包含重要人脸信息的向量,由其构成一个新的人脸特征空间,称其为特征脸。后续将待识别人脸与特征脸进行比较,从而完成人脸识别的过程,其识别流程如图1所示。
1.1 传统PCA的特征抽取
选择一定数量的人脸图像构成训练集,剩余的图像作为待测试的样本。假设人脸库中图像尺寸均为m×n,则其可以表示为一个列向量X=[x1,x2,…,xm×n]T。如果有M幅训练图像,构成的训练集如式(1)所示:
TrainSamples=[X1,X2,…,XM] (1)
將训练集中的每个向量减去训练集的均值向量mx,可得新训练集,如式(2)所示:
ctlSamples=[X1-Mx,…,XM-mX] (2)
根据式(2)可以得到其协方差矩阵的表达式,如式(3)所示:
(3)
其中,协方差矩阵C的大小为(m×n)×(m×n)。为了降低求解矩阵C的特征值和特征向量的计算量,引入奇异值分解(SVD)方法来解决计算过程中矩阵维数过高的问题[3,4]。
设矩阵C的特征值为λi,对应特征向量分别为ui和vi(i=0,1,…,M-1),则矩阵C的特征向量可表示为式(4):
(4)
对特征值进行降序排列,通过选择保留一定数量的特征值及其特征向量,以此构成特征脸空间。特征值的选择可以由累积贡献率(或阈值)决定,其计算公式如式(5)所示:
(5)
1.2 测试样本和训练样本的比较和分类
通过计算在N维空间中图像间的距离,可以测量图像之间的相似性。进行人脸识别时,有多样的分类器供人们选择,本文进行的人脸识别实验采用K近邻算法。其思想是计算待测样本和所有训练样本的向量距离,从中选取一定数量的最小距离,根据这些最小距离对应的训练样本中,大多数样本所属的类别,判断出待测样本属于哪个类别[5]。算法示例如图2所示。
1.3 实验结果分析
本节以ORL人脸库作为实验样本库,进行基于PCA算法的人脸识别测试。其中,ORL人脸库由40个人、每人10幅共400幅灰度图像组成,部分图像的背景为黑色,也有光照条件、脸部表情、细节等等外界条件的变化;K近邻分类器采用三阶近邻作为判别依据,实验结果如表1所示。
从表1可以看到,随着训练集的样本数增多,系统的识别精度也会越高。当样本数一定时,随着累积贡献率的增大,识别精度也会有提升,当高于85%时,系统的识别精度变化不大。因此在设置参数时,选择合适的累积贡献率值和样本数量,不仅可以降低训练过程的计算量,还可以使系统保持较高的识别精度。
2 基于分块PCA的人脸识别
PCA方法抽取的是图像的全局特征,而随着人脸像素的增多,其会丢失一些重要的局部信息,导致人脸识别的效率下降。为了解决这个问题,有学者针对特征抽取方面进行改进,提出了分块PCA算法[6]。其流程图如图3所示。
2.1 基于分块PCA的人脸识别算法
分块PCA的主要思想是先将一个m×n的图像矩阵X,分解为i×j块图像矩阵,从而通过式(3),使用PCA和奇异值分解方法,对这i×j个协方差矩阵进行特征提取操作,得到i×j个新的子特征脸。在子人脸图像经过新的特征脸投影到低维的线性空间后,将所有低维向量组合起来得到一个完整的训练集。后续的识别过程与传统PCA人脸识别算法一致。图像的分块方式如图4所示。
2.2 基于MPCA的人脸识别算法
为了进一步改善基于分块PCA的人脸识别系统的性能,在分块PCA方法的基础上,有学者提出一种针对分类过程的改进方法,称为MPCA。
在训练样本和测试样本经过子特征脸空间映射到低维空间后,均能得到i×j个子向量集。此时直接进入分类阶段:
(1)计算子训练集与测试样本子块之间的距离;
(2)将每组的所有子块的距离相加,得到数个测试样本与训练样本的距离;
(3)通过分类器进行分类并得出识别结果。其示意图如图5所示。
2.3 实验结果分析
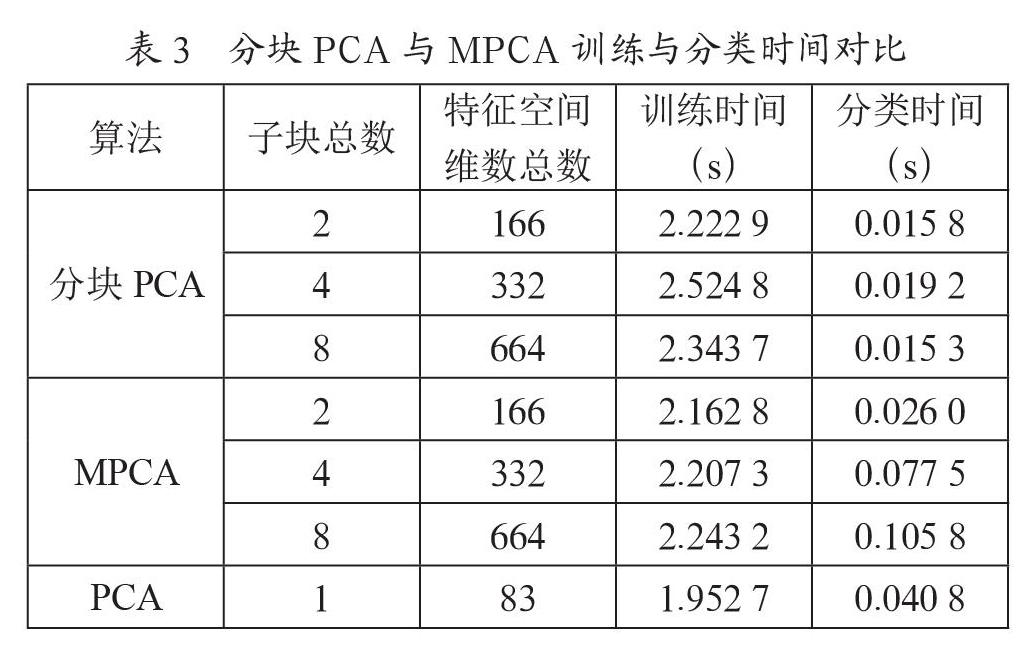
本节实验主要是与第一节中的基于分块PCA的人脸识别进行精度以及训练、识别分类时间的对比。选择每人的前5幅人脸图像构成训练集,剩余人脸图像作为测试样本进行分类识别测试。详细对比如表2和表3所示。
从表2中可以看出,在不同的分割方式情况下,基于MPCA的人脸识别的识别精度均高于基于分块PCA的人脸识别,大体上提升了2到3个百分点。
从表3中可以看出,基于MPCA的人脸识别在训练时所耗费的时间稍低于分块PCA,而分类识别中耗费时间高于分块PCA,但这种方法在统计上能够尽可能地减小或消除图像噪声等不必要的信息对识别分类过程所造成的影响,提高了人脸识别系统的识别性能和工作效率。
3 基于2DPCA的人脸识别
2DPCA(二维PCA)PCA和传统PCA的区别在于,2DPCA并不需要对图像进行一维转换的处理,直接将图像堆叠来获得协方差矩阵[7]。
3.1 2DPCA的特征抽取
向量X表示一个n维的列向量,通过一个线性关系,将一个m×n的图像矩阵A在向量X上进行投影,如式(6)所示:
Y=AX (6)
其中,X为投影轴;Y是图像矩阵A的投影特征向量。投影向量Y的分散程度越高,投影轴X越好,两者的关系式如式(7)所示:
J(X)=tr(SX) (7)
其中,SX是特征向量Y的协方差矩阵;tr(SX)是这个协方差矩阵SX的迹。当式(7)取得最大值的時候,可找出一个投影轴X,当所有的训练样本投影在它上面时,特征向量的总体散布矩阵最大。其中,协方差矩阵SX的迹如式(8)所示:
tr(SX)=XTE[(A-EA)T(A-EA)]X (8)
假设有M个大小为m×n的图像矩阵A,mx为这个样本集的均值向量,则协方差矩阵可由式(9)表示:
(9)
则式(7)变为式(10):
J(X)=XTGtX (10)
其中,X就是经过归一化处理的正交向量。这个准则也叫作广义总体散布准则。如果存在一个向量X,能够使这一个准则最大化,那么这个向量X就是最佳投影轴。这个向量X可以通过选取一定数量协方差矩阵Gt的最大特征值对应的特征向量组成投影矩阵获得[8]。
3.2 实验结果分析
实验主要对PCA、分块PCA、MPCA和2DPCA进行识别性能的对比,分别选择每人前1至5幅人脸图像构成训练集,其余人脸图像作为测试样本进行分类识别测试。识别精度和训练时间对比详细结果如表4和表5所示,PCA与2DPCA的重构图像对比如表6所示。
对比表6中两组重构的人脸图像,不难看出,2DPCA能够以更少的主成分来重构出效果比PCA更好的人脸图像。当选择80个主成分进行重构时,肉眼基本看不出重构图像和原始图像的区别。说明2DPCA的主成分保留了更多原始人脸图像的重要信息,因此在基于2DPCA进行人脸识别时,只需要选择更少的主成分就可以达到不错的效果。而抽取特征过程的计算量也会明显下降,这两点在表5中已经体现出来。当2DPCA选择20个主成分进行特征抽取时,中间过程耗费时间明显低于其他三种方法,而且识别精度与基于分块PCA的人脸识别的精度相当。
4 人脸识别仿真系统的设计和实现
4.1 仿真系统的开发环境
本文的人脸识别仿真系统是在Windows系统上实现,内存为8 GB,中央处理器为Intel(R) Core(TM) i5-3337U CPU @1.80 GHz 1.80 GHz。工具使用MATLAB R2014a中的GUI设计工具。运行流程图及仿真系统界面,如图6和图7所示。
4.2 实验结果分析
在本文设计的人脸识别仿真系统中,四种分析方法均选取每人前5幅人脸图像构成训练集,剩余图像可以用于进行分类识别测试,每种算法选取5组数据取平均值,结果对比如表7所示。
从表7中的数据可以看出,人脸识别的仿真系统在正常运作时,MPCA的识别精度最高,可达到约87.5%,2DPCA虽然识别精度不如其余两种分块PCA方法,但抽取特征的时间远低于其他两种方法。结论基本与前面的实验结果相符。因此在实际应用人脸识别时,可按照自己的需求来选择不同的抽取特征的方法。
5 结 论
本文主要完成了PCA其改进算法的分析并对它们进行了有效性评价,最终实现了人脸识别的仿真系统。尽管人脸识别技术现今有一定的成熟度,但不可否认这项技术仍然具有巨大的发展空间。追求系统的高识别精度和高效率无疑还是该项技术重要的研究课题。
参考文献:
[1] 李武军,王崇骏,张炜,等.人脸识别研究综述 [J].模式识别与人工智能,2006,19(1):58-66.
[2] 董琳,赵怀勋.人脸识别技术的研究现状与展望 [J].安防科技,2011(10):22-26.
[3] 李颖,张培珍,李灿苹.基于KL变换的人臉识别系统的设计与实现 [J].科技资讯,2009(20):218-219.
[4] 周又红.略谈矩阵奇异值分解定理 [J].工科数学,1996(3):125-126.
[5] 曾勇.广义近邻模式分类研究 [D].上海:上海交通大学,2009.
[6] 陈伏兵,杨静宇.分块PCA及其在人脸识别中的应用 [J].计算机工程与设计,2007(8):1889-1892+1913.
[7] 孙艳娜.基于2DPCA的人脸识别方法 [D].西安:西安电子科技大学,2013.
[8] YANG J,ZHANG D,FRANGI A F,et al. Two-dimensional PCA:a new approach to appearance-based face representation and recognition [J].IEEE transactions on pattern analysis and machine intelligence,2004,26(1):131-7.
作者简介:郭磊(1982—),男,汉族,黑龙江哈尔滨人,讲师,博士,研究方向:图像处理与机器视觉;通讯作者:周文杰(1996—),男,汉族,广东佛山人,助理工程师,本科,研究方向:图像处理。

