基于初始扰动的蜂窝夹芯板压缩屈曲载荷分析方法
奚 蔚,郑晓玲,汤家力,王春寿,林德志
(1.中国商飞上海飞机制造有限公司,上海 201324) (2.中国商飞上海飞机设计研究院,上海 201210)
先进碳纤维增强复合材料具有比强度高、比刚度大和可设计性强等优点,在航空结构中得到了广泛应用[1-3]。其中,蜂窝夹芯板作为一种特殊的复合材料,常用于飞机襟副翼、方向舵和升降舵等结构[4],其承受气动和操纵载荷,受载复杂,主要失效模式为屈曲失稳[5],因此有必要对其结构的稳定性进行研究。
唐劼尧等[6]基于连续介质损伤力学的损伤演化模型,采用试验和仿真方法对碳纤维复合材料蜂窝夹芯板的压缩稳定性进行了研究。Asprone等[7]通过设置不同的材料和厚度属性,研究了缺陷对蜂窝板稳定性的影响。Yang等[8]开发了一种简化的六边形单胞结构有限元模拟方法,对蜂窝板在轴向压缩载荷下的屈曲特性进行了预测。杜正兴等[9]进行了两种芯材厚度蜂窝板的轴压稳定性试验,采用多种工程方法和有限元方法计算了屈曲破坏载荷,通过计算结果与试验结果的对比给出了方法使用建议。张铁亮等[10]通过建立考虑芯层几何特征的有限元模型进行屈曲分析,并研究芯层几何参数对结构稳定性的影响。
本文提出了一种蜂窝夹芯板压缩屈曲载荷分析方法,该方法在有限元模型中引入初始扰动,以内外面板应变变化趋势发生背离时的载荷作为屈曲载荷,进行了不同长、宽和蜂窝高度板的压缩试验,通过将分析结果与试验结果对比,验证了方法的合理性。
1 屈曲载荷分析方法
首先介绍3种计算方法,即工程中常用的工程法、线性有限元法,以及本文提出的基于初始扰动的非线性有限元法。
1.1 工程法
矩形蜂窝夹芯板单轴压缩时,上下面板的屈曲临界应力为[11]:
(1)
式中:σcri为面板i(i=1代表上面板,i=2代表下面板)的屈曲临界应力;Eai为面板i在长度方向上的等效弹性模量;ti为面板i的厚度;h为上下面板形心间距离;b为受载边长度(即试验件宽度);λi=1-νabiνbai,νabi和νbai分别为面板i在长度方向和宽度方向上的等效泊松比;K为屈曲载荷系数。
K的计算公式为:
K=KF+KM
(2)
式中:KF为依赖于表板刚度和表板长宽比的理论系数;KM为依赖于夹层板弯曲刚度、剪切刚度及长宽比的理论系数。
KF的计算公式为:
(3)
式中:KM0为中间过程变量V=0时的KM值。
KM的计算公式为:
(4)
式中:Ψ1,Ψ2,Ψ3,Ki,Bi,Φi,R为中间过程变量,i=2;c4的值取决于板的长宽比a/b、板屈曲的纵向半波数n和板的边界条件。中间过程变量的计算公式如下:
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)

Q,BUL,αi,βi,γi,Ai计算公式为:
(13)
γ2K1)
(14)
(15)
βi=αiνabi+2γi
(16)
(17)
(18)
式中:Ebi为面板i在宽度方向上的等效弹性模量;Gbai为面板i面内剪切模量。
由此求得上、下面板屈曲临界应力后,分别乘以上、下面板面积再求和,就可得到压缩屈曲临界载荷Ncr。
1.2 线性有限元法
采用ABAQUS软件建立有限元模型,蜂窝芯材用各向异性材料模拟,采用C3D8六面体单元划分网格;内外面板各铺层用单向带模拟,采用S4四边形单元划分网格。利用子空间特征值求解法进行线性屈曲载荷分析,得到各阶特征值,最小特征值与加载载荷的乘积即是屈曲载荷。
1.3 基于初始扰动的非线性有限元法
由于实际结构不可避免存在构件初弯曲、载荷初偏心、截面形状不均匀或材料性质缺陷等不完美因素,所以受压后垂直于壁板方向的变形随载荷增加呈非线性变化,其失稳多属于几何非线性问题,计算比较复杂。本文在有限元模型中引入初始扰动,用初始扰动来反映上述各种不完美因素对结构屈曲载荷承载能力的影响。
首先,同线性有限元法一样,进行线性屈曲载荷分析,算出特征值,并将节点位移输出到指定格式文件中。然后,将特征值分析得到的正则化节点位移乘以一定的比例因子(本文取5%的壁板厚度),作为节点位置偏移量即初始扰动,利用IMPERFECTION关键字将初始扰动施加到各节点上。最后,对带扰动结构进行几何非线性静力分析,寻找垂直于壁板方向变形的最大点,以该点处内外面板应变变化趋势发生背离时的载荷作为屈曲载荷,如图1所示。

图1 屈曲载荷点示意图
2 蜂窝夹芯壁板压缩载荷试验
蜂窝夹芯壁板试验件如图2所示,试验件材料见表1,试验件铺层为[(±45)/0/(±45)/0/(0/90)/0/(±45)/0/(±45)]/蜂窝/[(0/90)/(±45)],包含4种试验件尺寸,见表2。试验采用端部加载方式,侧边采用滚针支撑以模拟简支条件,试验夹具及试验件安装示意图如图3所示,试验在200 t MTS静力试验机上进行,试验环境为室温大气环境。

图2 蜂窝夹芯壁板试验件示意图

图3 压缩试验夹具及试验件安装示意图

表1 试验件材料
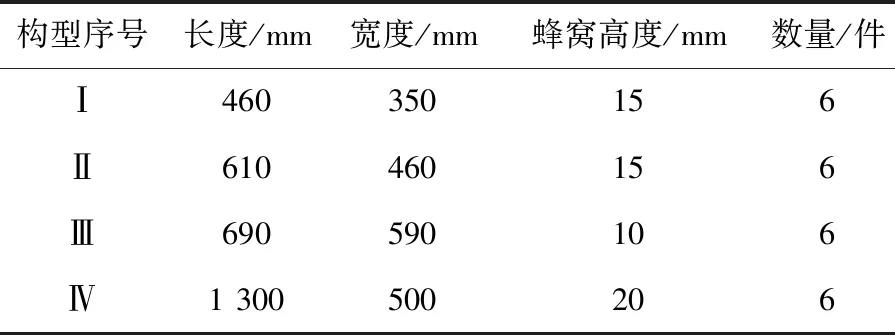
表2 试验件尺寸
各构型试验件均表现为整体屈曲破坏,典型破坏模式如图4所示,壁板在一侧凸起,在另一侧凹陷,各构型试验件屈曲载荷试验结果分别见表3~表6。

图4 试验件典型压缩失稳破坏图片

表3 构型Ⅰ试验件屈曲载荷试验结果

表4 构型Ⅱ试验件屈曲载荷试验结果

表5 构型Ⅲ试验件屈曲载荷试验结果

表6 构型Ⅳ试验件屈曲载荷试验结果
3 分析方法对比
采用第1节介绍的3种方法对屈曲载荷值分别进行分析,其中线性和非线性有限元法分析过程中需要建立有限元模型,模型中材料性能参数取值见表7。
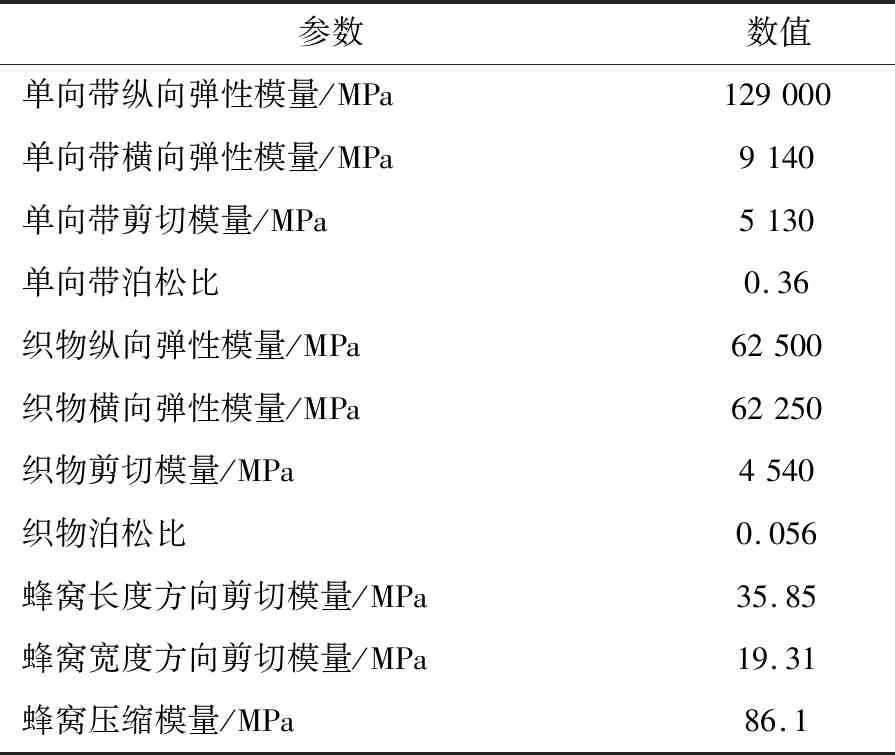
表7 材料属性
表2中构型Ⅰ试验件(尺寸460 mm×350 mm)的线性有限元分析正则化位移云图如图5所示,一阶特征值为2.182 5,有限元模型施加载荷为100 kN,所以线性屈曲载荷为218.25 kN。基于初始扰动的非线性有限元法分析结果如图1所示,屈曲载荷为140 kN。其他构型试验件的分析过程类似,在此不再赘述。

图5 构型Ⅰ试验件线性有限元分析位移云图
3种方法屈曲载荷分析值与试验值的对比见表8。由表可见,工程法分析值远远高于试验值,在蜂窝高度较小时的误差低于蜂窝高度较大时。线性有限元法分析值也高于试验值,但误差比工程法小。本文提出的基于初始扰动的非线性有限元法分析值与试验值吻合较好,且误差在13%~20%,预测精度较稳定。

表8 屈曲载荷分析值与试验值对比
4 结束语
本文提出了一种基于初始扰动的蜂窝夹芯壁板压缩屈曲载荷分析方法,通过引入初始扰动来考虑构件初弯曲等因素对屈曲载荷的影响,并对带扰动结构进行几何非线性有限元分析,以内外面板应变变化趋势发生背离时的载荷作为屈曲载荷,进行了不同长、宽和蜂窝高度的蜂窝夹芯板压缩试验,依据试验结果,对工程法、线性有限元法和基于初始扰动的非线性有限元法等3种方法的预测效果进行了对比,结果表明工程法和线性有限元法预测结果高于试验值,本文方法预测结果与试验结果吻合较好,且误差大小比较稳定。

