一种基于改进的动态规划思路的众核软件映射算法
覃志东, 冯 莹, 肖芳雄
(1.东华大学 计算机科学与技术学院,上海 201620;2.金陵科技学院 软件工程学院,江苏 南京 211169)
0 引 言
服务器多线程程序在操作系统调度下并发执行,其执行状态具有固有的不确定性,并在访问共享资源时,易导致竞争与死锁等问题.Lee等[1]认为,一些具有更细粒度并行性的嵌入式程序需用数据流图描述,并遵循任务间的结构和依赖关系,采取离线分配与调度方式向处理器映射,可有效提升系统的可预测性和可靠性.众核软件映射属于NP-hard问题,当前无法设计出多项式时间复杂度的确切解算法.对此,研究者往往结合问题实际,设计出近似算法或者启发式算法进行求解[2-3].此外,众核软件映射的具体方式有两种:一是处理器核心流水线执行方式[4];二是处理器核心并发执行方式[5].就如何最大化系统吞吐率的问题,文献[4]通过对任务图的多次均衡双划分来达到提升系统吞吐率的目的.但该方法一方面可能会导致任务分配不均衡性的累积效应;另一方面无法适用于处理器核心是奇数的场景.文献[6]提出了基于模拟退火思路和贪心法则的任务图划分算法(SAATSA),但该算法属于启发式近似算法,在求解过程中易陷入局部最优解.动态规划通过拆分问题,以递推的方式求解,易获得全局最优解,在诸如库存管理、资源分配等问题求解方面取得较好的效果.此外,在软硬件划分方面,文献[7]也基于动态规划思路提出了一种优化的算法.
本研究在剖析了众核软件基于流水线方式映射问题的基础上,提出了一种基于改进的动态规划思路的众核软件映射算法,该算法在获得最大吞吐率方面获得了较好的效果.
1 软件映射问题
1.1 基于处理器核心的流水线映射方式
众核软件内部结构与任务模块之间的依赖关系可以用有向无循环图G(V,E)表示.其中,V代表任务负载,E表示任务间的通信量与方向.对任务集的分配即是在满足任务之间的依赖关系的基础上对图G(V,E)进行划分.如图1所示,对边(ab,bd,ce)进行切割,可得任务子图G1(V1,E1)、G2(V2,E2)、G3(V3,E3)、G4(V4,E4).用C代表切割边集合,则该图的划分可表达为,

图1 任务图划分示意图
(1)
任务图划分后,得到的各任务子图向处理器平台上的对应核心映射,便实现了任务子集向核心的映射,如图2所示.而处理器核心按照任务子图间的依赖关系先后执行,便构成了核心的执行流水线[4-6],其流水周期由最长执行处理器核心2决定,如图3所示.显然,流水线填满后,每过一个流水周期T,系统就有一个输出,而各任务子图负载越均衡,周期T越短,系统吞吐率越大.
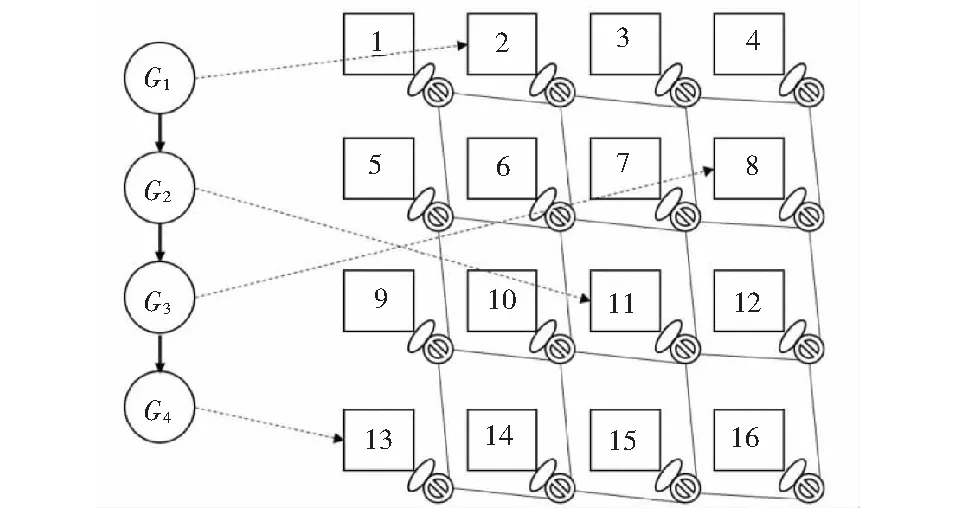
图2 任务子图向处理器核心映射示意图
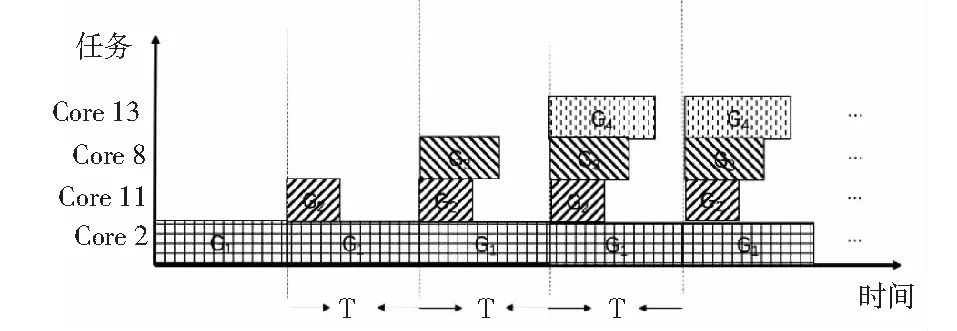
图3 处理器核心流水线执行方式示意图
1.2 众核软件映射问题的形式化描述
1.2.1 众核软件映射过程剖析
为便于映射算法的设计,本研究用一个问题实例来展示任务映射与绑定的流程,并分析相关的细节问题和影响吞吐率的因素.
(1)逻辑处理器抽象.图4中,(A)是一个具有四核心的物理处理器.根据各核心的个数、互联方式以及缓存的设置方式等,可以把物理处理器抽象为逻辑处理器,如图4(G)所示.其中,物理核心Core3被抽象为逻辑核心P2,而物理核心Core2被抽象为逻辑核心P3.真实的众核处理器上核心很多,有些核心甚至坏掉,在使用时,可以根据具体情况选择一些核心来使用,并把它抽象成逻辑处理器[8].
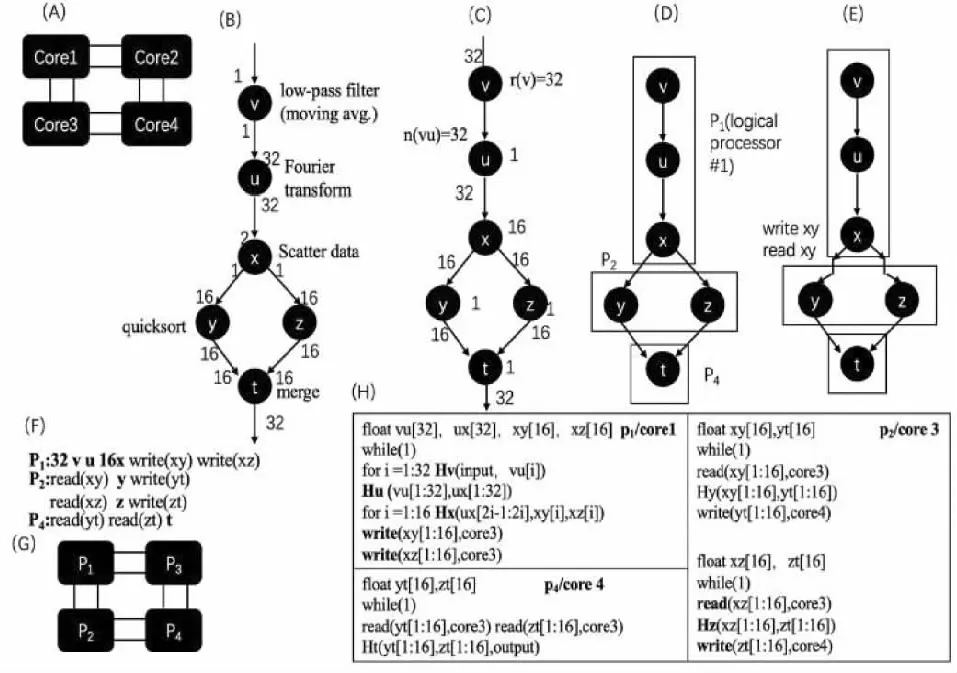
图4 众核软件映射过程示例图
(2)数据流图分析与转换.图4中,(B)是用同步数据流图(SDF)表示的一个众核软件例子.该软件由6个任务v、u、x、y、z和t组成,分别实现低通滤波、傅里叶变换、数据分发、数据快插和数据融合.其中,v运行1次要消耗1单元的数据并产生1单元数据.u运行1次要消耗32单元的数据并产生32单元数据.所以,为满足软件系统的正常运行,v需要连续运行32次,u才运行1次,而x需16次,y、z和t各需1次.此时,通信量为32.可把这种调度平衡后的负载与通信用有向无循环图4(C)表示.目前已有很多算法解决SDF图的平衡调度[9],平衡调度好的SDF图可以直接用有向无循环图表示,供划分映射.
(3)软件向逻辑处理器映射.此阶段由映射算法把图4(C)的有向无循环图向逻辑处理器映射,如图4(D)所示.假定,v、u、x映射到P1,y、z映射到P2,t映射到P4,便构成了一个3段流水线.最大化这个流水线吞吐率,是本研究要解决的问题.但问题的解决需要考虑任务绑定在核心上的具体情况.
(4)软件任务向处理器核心绑定.如图4(E)和(H)所示,划分好的任务集需要绑定到映射的逻辑核心所对应的物理核心.如y、z对应的是逻辑核心P2,要绑定到物理核心Core3.此时,需要根据任务间的相对位置建立通信.若2个任务在一个核心上,那么定义数组变量,完成数据通信,如vu[32]便是v对u的通信.若两者不在一个核心上,那么要定义数据发送/接收函数,如write(xy[1∶16],core3)便是x向y所在的Core3的缓存写数据,而read(xy[1∶6],core3)便是y把x写在本地缓存的数据读出来.显然,write函数是跨越处理器核心的,其通信时间是受具体通信链路决定的.为了让任务利用以及产生通信数据,还要对任务加上封装函数,如Hu(vu[1∶32],ux[1∶32]).
1.2.2 问题形式化描述
事实上,任务分配并绑定到核心后,虽然要对任务打包封装并建立核心内任务间通信变量,但是其额外的开销与任务本身的负载相比可以忽略[4].真正影响系统吞吐率的因素是任务的负载和核心间任务的通信代价.所以,为了最大化吞吐率,首先映射到核心上的负载需均衡.即分配到不同核心的任务子图的最大负载量和最小负载量之差应尽可能地小,如式(2)所示,
(2)
式中,N为划分的子图数;wi为各子图的负载量.
另外,核心间任务的通信代价与处理器的缓存的配置有关.当采用集中式缓存时,核心共享缓存,核心间通信的write和read函数都需要经过片上网络对该缓存进行操作;当采用分布式缓存时,read不需要使用片上网络,write则需要[10].
本研究针对分布式缓存建模,具体如图5所示.对于图1中边ab,若任务a和b在不同的核心执行,任务a需通过片上网络向任务b所在核心的私有缓存写入3单元的数据量,任务b再从自己的私有缓存读取数据.但这种通信方式对于任务a所在核心要产生额外的通信代价.因此,为最大化吞吐率,任务图划分时,需尽量减少通信代价,如式(3)所示,

图5 不同处理器上的任务通信方式示意图
mineεC{n(e)}
(3)
式中,C为所有切割边集合;n表示通信代价.
基于以上分析,则基于流水执行的众核软件映射问题可以形式化表达为下式,
minimizeQ
Q=F{‖wi‖,‖C‖}
s.t.V1∪V2∪…∪Vn=V
E1∪E2∪…∪EN∪C=E
(4)
式中,成本函数Q以系统的执行周期进行建模,是系统吞吐率的倒数.
2 基于吞吐率优化的软件映射算法设计
2.1 改进的动态规划优化算法思路
本研究以动态规划算法作为基本优化思路,并对其进行了2方面改进.
2.1.1 动态更新可选结点
区别于一般动态规划算法,可选结点虽然也只有2个状态:可选和不可选,但不可选是由2个原因造成:已经被选择了或存在依赖关系.所以,改进的动态规划算法每选择一个任务结点时,考虑依赖关系的变化,并实时更新可选结点(可选的值).
2.1.2 动态调整期望值exp
由于任务结点负载值具有颗粒性,利用动态规划思路对任务图进行划分时,子图结点的负载以及通信代价之和有时不会正好等于期望值.当出现加上该结点的子图的负载超过了期望值时,此时需要比较在没有加上这个结点和加上了这个结点时的负载之和跟期望值之间的距离大小,并选择距离较小的那种方案.因此,在对任务图进行划分时可以将问题简化为:对于一些结点(此时的可选结点是动态变化的),在限定总负载之和的情况下,如何划分使得负载之和跟期望值距离最近,用公式表示为,
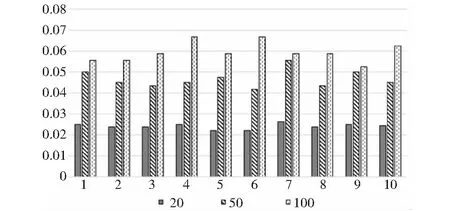
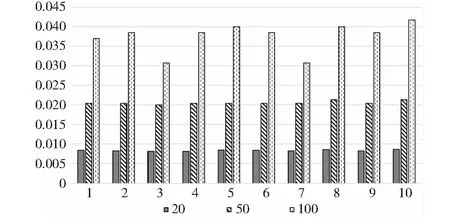
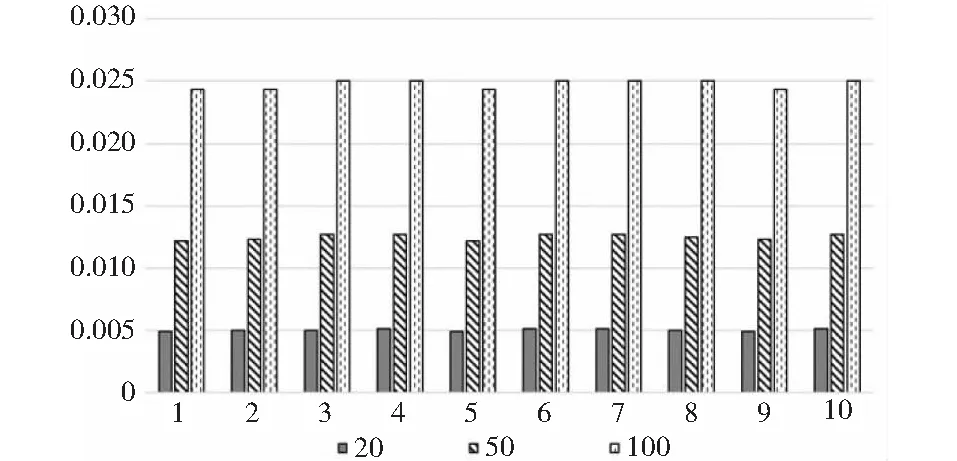
min1 (5) 式中,exp表示期望负载,绝对值表示实际负载和期望负载的差值,其目标就是尽可能地让差值最小. 如果按照上述方法,便会出现负载之和大于或者小于期望值的情况.为了减少子图间负载之和的差距过大对系统吞吐率的影响,本研究使用动态调整子图期望负载的机制.即除了第一个子图,其余的子图的结点的负载之和由其前面所有子图的负载决定,每产生一个新的子图,则需要动态改变允许负载的期望值.例如,在对任务图进行划分时,从第一个任务子图到倒数第二个任务子图的负载之和一直小于(大于)期望值,那么最后一个子图的期望值便可能会很大(很小).如表1所示,在对一个任务图进行划分时,最初设定的期望负载值为40. 表1 采用动态调整大小机制所对应的子图负载 表1中,第一行数据为未采用动态调整子图期望负载所对应的最终划分好的各个子图的负载值,该划分形成的流水线周期为59单位时间.而第二行数据为采用了该机制后所对应的各个子图的负载值,该划分形成的流水线周期为42单位时间.显然,采用动态调整子图期望负载进行图划分后,各个子图的负载更均衡,形成的流水线周期更小,流水线的吞吐率更大.在子图划分时,子图动态期望负载由式(6)决定, (6) 改进的动态规划算法伪代码如下: 算法1:改进的动态规划算法/∗options//可选结点w[]//任务结点的负载flag[]//结点的状态C//子图的期望负载m[]//状态转移方程对应的值n//任务图结点个数result[]//最优解的值,以及选择的结点 ∗/optionsupdateNode(G)for var i0 to c for var j0 to jfor var k0 to j for var l0 to options,length if(flag[l]==1) if(m[i-1][k]+w[l]≤j) if(result[i-1]) 基于动态规划思路的软件映射算法(dynamic programming mapping algorithm,DPMA)伪代码如下: 算法2:基于改进动态规划的软件映射算法/∗Dynamin()//改进的动态规划算法getCost()//计算通信代价之和G//任务图N//需要划分的子图个数options//可选结点Gi//被划分成的子图updateNode()//更新可选结点add()//将结点加入到子图中updateCost()//更新子图的期望值results//记录最优解所对应的结果Best//记录当前最优解∗/optionsundateNode(G)best0for var x 0 to N for var i0 to options,NodeNum Giadd(Dynamin(options,exp)) resultsGiif(getCost(results)>best)){ bestgetCost(resluts)optionsupdateNode(Gi)expupdateCost(i1 getWordload(Gi)) DPMA算法的基本步骤如下: (1)对任务图进行拓扑排序,更新可选结点,计算第一个子图的期望值. (2)利用改进的动态规划的思路在满足子图的负载以及通信代价之和小于期望值时,求出放入1个结点时到放入n个结点时所对应的最优解.其中,n是一个不确定的数.当子图的负载以及通信代价之和接近期望值时,该子图划分完毕,开始构建下一个子图. (3)更新该子图中的结点,更新可选结点. (4)重复步骤(2)、(3),直到最优解的值等于期望值或者一直是某个数值保持不变,此时一个子图构建完成. (5)根据已构建完的子图,更新子图负载的期望值. (6)重复步骤(2)、(3)、(4)构建下一个子图,直到已有的子图的个数等于既定的子图个数. 为了进一步分析改进后的基于动态规划思路的软件映射算法的性能,本研究从文献[11]中的网站下载了包含300个任务的任务图模型,每个模型中包含任务的负载、任务之间的依赖关系等信息.然后从中随机选取10个文件进行对比实验.在设计算法时,首先需要对任务图中的数据进行处理,筛选出有用的数据,接着再基于数据做进一步的实验分析.本实验采用java语言实现,程序的运行环境为Mac Os. 实验中,利用文献[4]的DPTAA算法、文献[6]的SAATSA算法以及本研究的DPMA算法将任务图划分成20、50、100个子图,分别映射到20、50、100核心的处理器上,结果如图6~图8所示.其中,横向代表随机抽取的10个任务图,纵向表示各任务图划分后子任务图负载以及通信代价之和的最大、最小值之差值与期望值之比. 图6 划分成20个任务子图3种算法对比情况 图7 划分成50个任务子图3种算法对比情况 图8 划分成100个任务子图3种算法对比情况 测试结果表明,经DPMA算法映射的系统在吞吐率方面优于其他2种算法的结果.其原因是DPMA算法相当于把一个映射问题划分成多个子问题,通过寻找每个子问题的最优解从而得到较好的最终解;而DPTAA算法属于近似算法,不断地切割图,可能导致结果变差;SAATSA算法通过不断进行邻域搜索,很可能陷入局部最优解. 利用本研究的DPMA算法将具有100、300、500个任务的任务图划分成20个、50个、100个子图并映射到处理器,结果如图9~图11所示.其中,横向代表选中的10个任务图,纵向表示系统的吞吐率.由图可见,将任务图划分为100个子图映射时,系统的吞吐率最大. 图9 100个结点任务图划分情况 图10 300个结点任务图划分情况 图11 500个结点任务图划分情况 吞吐率,按照定义来说,是单位时间内处理信息的量.若流水线周期T小,则流水线的吞吐率大.在对任务图划分时,随着子图个数的增多,每个子图的负载以及通信代价之和会降低,则所映射的处理器核心运行的时间就减小,导致流水线的周期T减小,系统的吞吐率变大. 本研究基于动态规划算法思路,设计出了一种高效的众核软件任务映射算法.利用该算法把众核软件任务映射到处理器核心上构成流水线执行,充分挖掘了众核平台和众核软件任务的并行性,能有效提高系统的吞吐率.特别地,由于系统的流水线执行状态相对简单,该映射算法较适合一些对系统状态可预计性和可靠性要求较高的领域.


2.2 软件映射算法设计

3 实验与分析



4 结 论

