基于相位幅值调制的聚苯乙烯小球非接触传输

张 鹏，董惠娟，初红霞，杜 娟，吴东艳

(1.黑龙江工程学院 电气与信息工程学院，哈尔滨 150050；2.哈尔滨工业大学 机电工程学院，哈尔滨 150001)

在生物学、分析化学、医药学等领域，非接触传输处理小颗粒和液滴得到了非常广泛的应用[1-4]。在众多的非接触处理技术中，声悬浮因其具有生物兼容性、被悬浮材料的独立性以及不需要对实验样品制备而得到广泛关注和研究[5]。用于非接触传输和处理物体的声悬浮器通常由1个或多个超声换能器和反射面组成[6]。当物体被稳定悬浮在悬浮器中时，可以通过改变超声换能器的电参数、悬浮器的声腔几何参数以及悬浮器本身或换能器的空间位置等方法来实现被悬浮物体的二维或三维可控移动[7]。FORESTI D等[8]使用一种由多个换能器组成的平面阵列，通过改变两个相邻换能器之间驱动电压的幅值，实现物体在空气中的水平传输。文章基于平面阵列式悬浮器，描述一种使用相位幅值调制(Phase and Amplitude Modulation，PAM)的驱动换能器阵元，实现被悬浮物体的水平平滑移动的方法。与单纯使用幅值调制的传输方法相比，通过同时改变换能器阵列中相邻阵元间驱动信号的相位差和幅值的方式，可使样本的传输过程更加平滑和稳定。文中对相位和幅值混合调制方法进行有限元仿真和实验研究，实现了聚苯乙烯小球在空气中的可控平滑移动。

1 数值模型

文中所使用的平面阵列式声悬浮器由5个谐振频率为f=20 kHz的郎之万压电超声换能器(Langevin Piezoelectric Transducer，LPT)和一个不锈钢反射面组成。超声换能器辐射面被设计成边长为D=15 mm的正方形，其辐射端材料为钛合金。5个超声换能器构成1×5水平线性阵列。该声悬浮器的二维简化ANSYS仿真模型如图1所示。

图1 1×5平面阵列式声悬浮器模型

图1中，坐标x表示水平方向，H为换能器阵辐射面与反射面之间的距离。W=90 mm为反射面的宽度。S为换能器阵元间距，被设定为0.5 mm。模型使用在x和z两个方向上具有位移自由度的结构单元构建辐射面和反射面，使用只具有声压自由度的声流单元来仿真辐射面和反射面之间的空气区域。对于空气区域与辐/反射面之间的相互作用问题，则使用具有位移和压力两个自由度的流固单元来解决。这些单元被应用在空气和辐/反射面之间，并通过在其接触面添加流固耦合标志(FSI)来仿真流固耦合问题。在阵元间隙处以及无结构覆盖的声场边界处使用无反射全吸收边界条件来仿真无限远空气区域。仿真中用到的换能器辐射面振幅由激光测振仪(OFV-505/500)测量获得，为12 μm。

在声悬浮器中，小尺寸物体会被捕获并悬浮在声场的势能极小值点处，而作用在小球上的声辐射力的时间平均声悬浮势能由式(1)给出[9]。

(1)

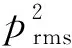
在ANSYS中，通过对有限元模型进行仿真计算，可以得到辐射面和反射面之间空气声场内的声压p分布。而式(1)中所需的空气质点振动速度v则可使用式(2)进行计算。

v=-▽p/(jωρ).

(2)

为了得到与被悬浮小球半径无关的悬浮势能，定义相对声辐射势能为

(3)

作用在被悬浮小球上的声辐射力F由式(4)计算得到，其相对声辐射力Fri则由式(5)计算得到。

Fi=-∂U/∂xi，

(4)

Fri=-∂Uri/∂xi.

(5)

式中：i表示第i个方向。

声辐射力在竖直方向的分量Fz用来克服使小球悬浮起来的重力，其水平方向的分量Fx则用来确定小球的水平悬浮位置。显然，在水平方向上，小球会悬浮在Fx=0的点上。同时，Fx还可以作为控制物体水平移动的推进力。当悬浮势能的节点位置发生水平移动时，悬浮的小球也会在这个水平分量Fx的作用下，跟随悬浮势能节点移动。

2 幅值调制传输过程分析

文中所述的1×5平面阵列式声悬浮器中，每个换能器均由一路幅值、相位、频率可编程设定的超声信号驱动[10]。依据FORESTI D等[8]的研究，当5个换能器的驱动信号电压幅值按照图2所示的规律变化且驱动信号的相位差Δφ始终为0°时，可以实现物体从LPT1传输到LPT5。整个传输过程可分为4个传输阶段。在每个传输阶段内，只有2个相邻换能器振动。

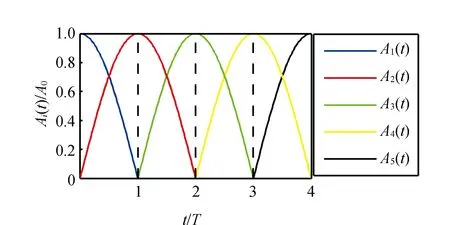
图2 5个超声换能器驱动信号的幅值变化

图2中，T为超声换能器驱动信号电压幅值的调制周期，指悬浮势能节点从1个换能器的轴线处移动到相邻换能器的轴线处所需的时间。Ai(t)表示第i个LPT的驱动信号电压幅值函数，其表达式为

(6)

图3给出使用上述驱动方法时，聚苯乙烯小球水平位置变化情况的仿真(蓝色圆圈)和实验(红色)曲线。其中，仿真曲线是通过对数值模型的仿真计算，获取相对声悬浮势能节点的坐标。在仿真和实验中，取换能器辐射面到反射面的距离为H=0.5λ，换能器辐射面振动频率为f=20 kHz。聚苯乙烯泡沫小球的直径为3 mm，调制周期T=4 s。

图3 聚苯乙烯泡沫小球水平传输的仿真和实验结果曲线(S=0.5 mm,f=20 kHz,A0=12 μm,H=0.5λ,T=4 s)

从图3可以看出，聚苯乙烯泡沫小球从LPT1传输到LPT5。小球的实验运动趋势与仿真结果基本吻合。小球在传输过程中有跳跃传输和振荡的现象发生，这种现象多发生在小球经过相邻LPT间隙的时刻。这是由于阵元间隙的存在和声场的不对称，改变了间隙下方的声场，使间隙下方无法形成稳定的悬浮势能节点，小球无法停留在间隙下方，而跳跃到相邻LPT下方。表1列出在使用幅值驱动方法条件下，不同传输阶段小球通过间隙时的跳跃传输距离Ds和振荡幅值Aosc。

从表1可以看出，在整个悬浮传输过程中，小球的最大跳跃传输距离为7.70 mm，最大振荡幅值为2.37 mm。跳跃传输距离越大，则对应的振荡幅值越大。显然，降低跳跃传输距离可以减少振荡幅值。值得注意的是，在传输阶段2T～3T，发生大幅跳跃传输和回跳振荡现象等不稳定传输现象，这是由装配误差以及LPT3和LPT4的谐振频差造成的声场分布不均匀而导致的。

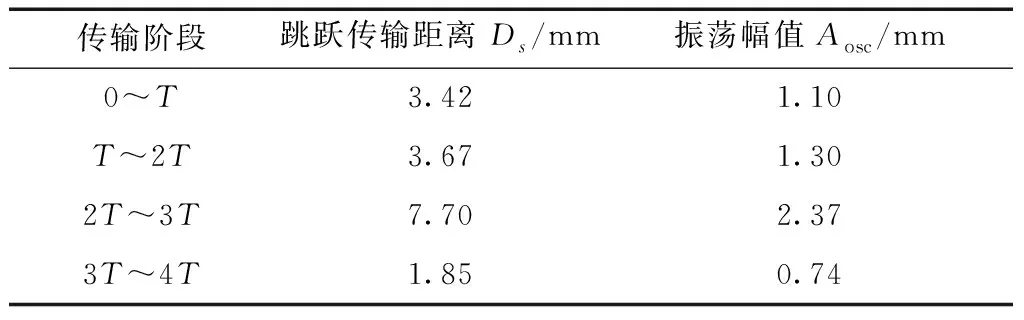
表1 使用幅值驱动方法时不同传输阶段小球通过间隙时的跳跃传输距离Ds和振荡幅值Aosc

3 相位对传输过程的影响

小球在传输过程中发生的跳跃和振荡现象会降低传输稳定性。实践表明，驱动信号的相位差可以改变声场中的悬浮势能分布，进而改变物体在声场中的悬浮位置。图4给出不同传输阶段相邻两个换能器驱动信号相位差为0°、±20°、±40°、±60°时，小球的水平悬浮位置仿真曲线。

从图4(a)、图4(d)可以看出，在传输阶段0～T和 3T～4T，水平悬浮位置变化规律相似。对于传输阶段0～T(见图4(a))，当Δφ12<0°时(LPT1的相位超前于LPT2)，水平悬浮位置曲线线性度较差，且偏离Δφ12=0°时的水平悬浮位置。相位差绝对值|Δφ12|越大，偏离现象越严重。当Δφ12>0°时，水平悬浮位置曲线线性度较好，跳跃传输改善情况明显。对于传输阶段3T～4T(见图4(d))，相位对水平悬浮位置的影响情况与阶段0～T相反。当Δφ45<0°时，水平悬浮位置曲线线性度较好。从图4(b)、图4(c)可以看出，传输阶段T～2T和2T～3T，水平悬浮位置变化规律相似。相位对传输跳跃现象改善不明显。当|Δφ23|和|Δφ34|大于等于20°时，水平悬浮位置偏离其0°时的曲线较严重。

表2列出相位差为0°、±20°、±40°、±60°时，不同传输阶段内，小球通过间隙时跳跃传输距离Ds的仿真数值。为了提高传输过程的稳定性，Ds应该越小越好。在4个传输阶段内，Ds的最小值分别为2.99 mm、5.47 mm、5.48 mm、2.99 mm，对应的相位差为40°、20°、-20°、-40°。

图4和表2可以确定，最优相位差Δφopt在4个传输阶段内的最佳取值范围分别是20°<Δφopt12<60°,0°<Δφopt23<20°，-20°<Δφopt34<0°，-60°<Δφopt45<-20°。同时，由于声悬浮器的结构对称，可得Δφopt12=-Δφopt45，Δφopt23=-Δφopt34。

表2 相位差为0°、±20°、±40°、±60°时，不同传输阶段内小球跳跃传输距离Ds仿真结果 mm

图4 小球的水平悬浮位置仿真曲线

为了得到不同传输阶段的最优相位差Δφopt，在相位差最佳取值范围内，对小球在传输过程0～T和T～2T中的跳跃传输距离Ds进行仿真，仿真结果见图5。

图5 0～T和T～2T传输阶段驱动信号相位差最佳取值范围内小球的跳跃传输距离仿真结果

由图5可知，0～T和T～2T阶段，相位差的最优值为Δφopt12=30°，Δφopt23=12°，此时物体的跳跃传输距离的仿真值最小，分别为Ds=2.5 mm、3.98 mm。比相位差为Δφ=0°时的跳跃传输距离分别减少了58.3%、27.5%。同时，可以确定2T～3T和3T～4T阶段的最优相位差分别为Δφopt34=-12°，Δφopt45=-30°。

4 聚苯乙烯小球的混合调制传输

依据上述仿真结果，设置传输过程中相邻换能器驱动信号相位差的变化情况如图6所示。

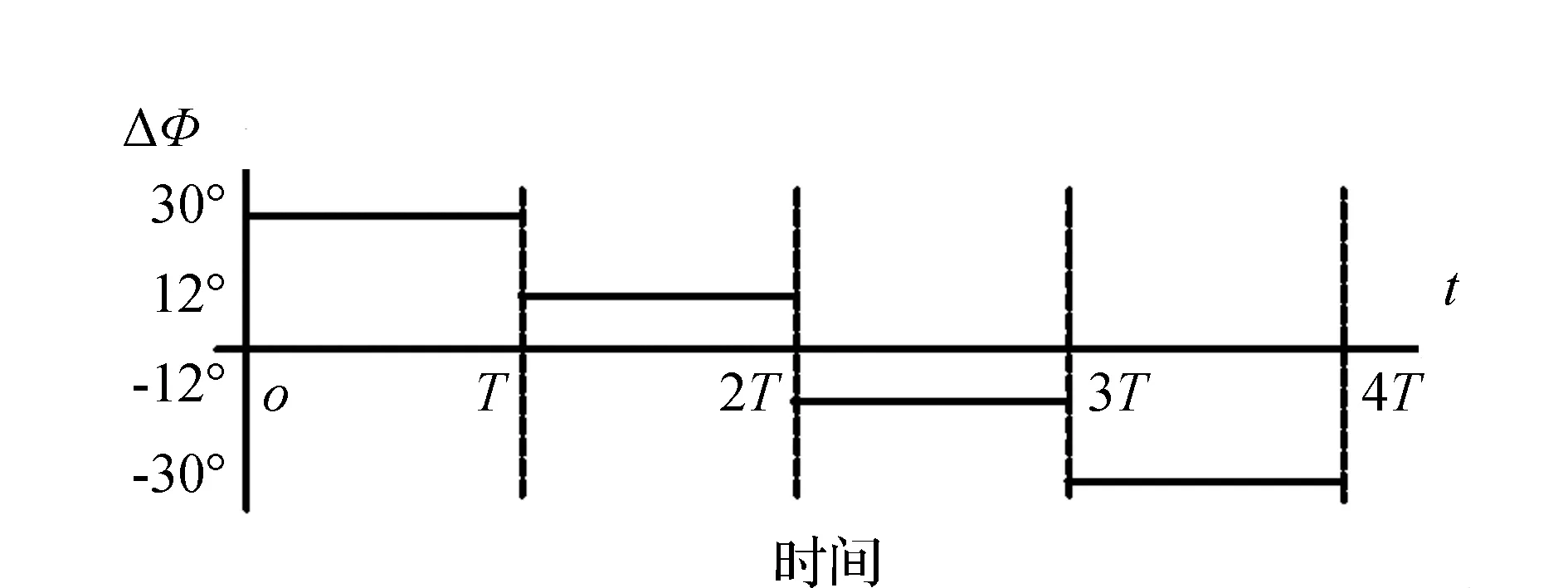
图6 传输过程中相邻换能器驱动信号相位差的变化情况

图7给出使用PAM驱动方法获得的聚苯乙烯泡沫小球水平悬浮位置的实验和仿真曲线。表3列出在使用PAM驱动方法条件下，不同传输阶段中，小球通过间隙时的跳跃传输距离Ds和振荡幅值Aosc以及相对于幅值驱动方法Ds和Aosc的减少比率。

图7 使用相位幅值调制驱动方法得到的聚苯乙烯泡沫小球水平传输的仿真和实验结果曲线

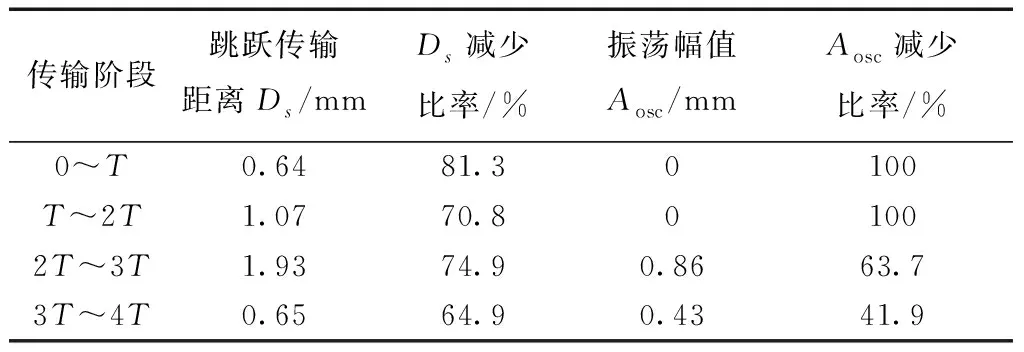
表3 使用PAM驱动方法条件下不同传输阶段小球的跳跃传输距离Ds和振荡幅值Aosc

由图7和表3可得，使用PAM方法可以有效改善传输过程中小球的跳跃和振荡现象。由于悬浮器的结构并没有改变，大幅跳跃传输和回跳振荡现象仍然发生在2T～3T传输阶段。在4个传输阶段中，Ds和Aosc的最大减少比率为81.3%和100%。在传输阶段0～T和T～2T,振荡现象消失。

5 结束语

在超声悬浮传输过程中，被悬浮物体在声辐射力的作用下，跟随悬浮势能节点移动。为了保证物体的传输稳定性，需要构建稳定连续的悬浮传输声场。对于文中所述的1×5平面阵列式超声悬浮器，阵元间隙、装配误差以及换能器阵元谐振频差等因素均会影响传输声场的连续和稳定，从而导致物体在传输过程中发生跳跃和振荡现象。为了提高小球在悬浮器中的传输稳定性，减弱甚至消除小球在传输过程中的跳跃和振荡现象，文中在传统的换能器阵元幅值调制驱动方法的基础上，提出一种相位和幅值混合调制的换能器阵元驱动方法。该方法引入相邻换能器驱动信号相位差作为辅助控制参量来补偿因换能器阵元间隙等因素导致的声场分布不均，显著减少了小球在传输过程中的跳跃传输距离和振荡幅值，提高了小球的传输稳定性。文中分析了幅值调制传输过程中小球的跳跃和振荡情况，并通过仿真确定不同传输阶段下，相邻换能器驱动信号的最优相位差。实验表明，悬浮传输过程中，物体的跳跃传输距离和振荡幅值分别减少了64.9%和41.9%。