半干旱环境下植被-沙模型的斑图动力学
曹佳会,李 莉
(山西大学 a.复杂系统研究所; b.计算机与信息技术学院, 太原 030000)
1 研究现状
近几十年来,我国干旱半干旱地区荒漠化现象越来越严重,保护植被系统刻不容缓。植被由于具有固沙、固碳、固水和释放氧气等多种生态功能而被誉为“生态系统工程师”[1]。植被的生长状况和覆盖率会受自然环境条件或人类活动的影响,如水、光照、降雨、风速、放牧等[2-4]。这些因素相互作用或单独作用将导致不同的现象。因此,关注这一主题将有助于更好地理解植被系统的发展演化规律。在空间或时间上具有某种规律性的非均匀宏观植被结构称为植被斑图[5]。特殊的植被斑图结构(如点状斑图)已经成为荒漠化预警的一个重要指标,因此明确植被斑图如何产生及其相变规律将为荒漠化的防治提供理论依据。
Klausmeier[6]于1999年首次提出了植被与土壤水相互作用的动力学模型,包括植被生物量和土壤水密度,并发现图灵失稳导致规则植被斑图结构产生,而微小的小尺度地形的变化可能会引起不规则植被斑图结构出现。Rietkerk等[1]在Klausmeier模型中引入地表水,建立了包含植被、地表水和土壤水的三变量植被模型,并指出半干旱地区植被斑图结构的形成主要取决于植被密度和地表水渗透之间存在的正反馈以及径流水在空间上的重新分配机制。
Meron等[7]建立了考虑水资源有限的植被模型,发现随着降雨量的增加,植被的空间分布结构经历了裸露的土地、点状、条状、间隙状等中间态,当降水量比较高时形成了均匀植被结构。随后,植被斑图形成的内在机制受到越来越多学者的关注[8-10],许多重要的数学模型被提出,用来解释自然界中广泛存在的各种植被斑图现象[11-14]。鉴于水资源在植被的生长和定植中起着重要作用,目前大部分的植被模型仅考虑水的影响。
事实上,其他因素也会影响植被斑图结构的形成机制,例如风、地形(坡度)、动物栖息等[12,15-18]。一些研究者发现,在干旱和半干旱的多风沙地区观察到垂直于主导风方向的带状植被斑图,如毛里塔尼亚、澳大利亚和马里等地区[16-18]。不同于无风条件下的植被,当风作为驱动力时,植被的生长会受到沙粒运动的剧烈影响。具体而言,即风沙的输移和沙丘会入侵植被区域,从而影响植被的生长。White等[19-20]认为风可能是带状斑图出现的驱动因素,而且孤立植被周围风吹物质的积累可能是植被带外扩的核心。Zhang等[21]基于反应扩散对流方程建立了一个植被-沙动力学模型,其中盛行风和非盛行风分别通过对流项和扩散项刻画,通过数值模拟发现在不考虑盛行风的情况下形成了迷宫状植被斑图,而在考虑盛行风的情况下最终形成的带状植被斑图垂直于盛行风的方向,这一结果揭示了澳大利亚西部皮尔巴拉中部地区迷宫和带状植被斑图的产生机制。Zhang等[22]的模型考虑了植被对沙的聚集效应会随着植被生物量的的增加而减少,直到植被生物量达到确定值,聚集效应将达到最低。事实上,在一些多风沙的地区,植被对沙的聚集效应会随着植被生物量的增加而增加,因此,在本文中主要考虑一种线性作用项的聚集效应机制,从多种形式的植被-沙模型方面更清楚地理解植被与沙的相互作用机制,进一步从理论的角度寻找植被斑图产生的内在机制。
2 数学模型
基于Zhang等[22]提出的包含植被生物量(V)和沙丘高度(S)的植被-沙模型:
(1)
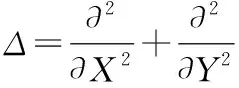
不同于Zhang等[22]考虑的植被对沙的聚集效应会随着植被生物量的增加而减少且植被生物量到达一定程度时会降到最低,这里考虑一种线性作用项的聚集效应机制,对应的模型(1)改进为:
(2)
为便于分析上述模型的动力学行为,通过对上述系统进行无量纲化处理,得到如下的系统:
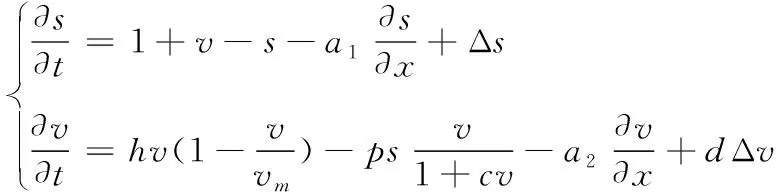
(3)
这里,
3 稳态的存在性和稳定性分析
首先,系统(3)对应的常微分系统为:

(4)
定义:
通过求解F(s,v)=0和G(s,v)=0,可以得到系统(3)存在如下平衡点:① 当v=0时,s=1时,系统(3)总是存在1个裸沙态平衡点E0=(1,0);② 当v≠0 时,可以推导出1个关于变量v的一元二次方程:
(5)
令
显然,系统(3)的平衡点个数取决于上述恒等式中各参数之间的关系。由参数的生物学意义可知b1=-ch/vm<0,进一步分为以下几种情形讨论:
1) 当参数满足条件
时,式(5)有2个正根:
因此,有s11=1+v11,s12=1+v12。可以得到系统(3)有2个均匀植被平衡点E11=(s11,v11),E12=(s12,v12)。
2) 当参数满足条件
时,式(5)具有唯一的正根:v2=-b2/2b1,同时s2=1+v2。因此,系统(3)具有平衡点E2=(s2,v2)。
3) 当参数满足条件
时,则式(5)不具有任何实根,表明系统(3)不存在平衡点。
为了讨论上述平衡点的稳定性,对系统(3)在平衡点E*=(s*,v*)附近进行线性化:
(6)
其中:
于是得雅可比矩阵:
综上所述,护理临床带教中实施分层次教学目标管理,应用价值较高,可有效提供带教效果,为实习生日后工作奠定良好基础,利于医疗事业良性发展。
特征方程为:
对于裸沙态平衡点E0=(1,0),可以得到:
λ2+(1-h+p)λ+p-h=0
当h 结合平衡点的生物学意义,应关注均匀植被平衡点E2。对于均匀植被平衡点E2,需讨论它的局部渐近稳定性。如果有以下条件 (7) 成立,对于系统(3),通过线性稳定性分析,可知平衡点E2是局部渐近稳定的。 c.c.+o(ε2) (8) 把式(8)代入线性化系统(6),得到如下特征方程: (9) 化简得到: λ2-trkλ+Δk=0 (10) 其中: trk=a11+a22-(a1+a2)ki-(1+d)k2= tr0-(a1+a2)ki-(1+d)k2 Δk=a11a22-a12a21- (a11d+a22+a1a2)k2+dk4+( a2k3+a1dk3-a22a1k-a11a2k) 通过分析,可得到特征值 (11) 这里, φ=(a11-a22-(1-d)k2)2- (a1-a2)2k2+4a12a21) ψ=-2(a11+a22)(a1+a2)k+ (1+d)(a1+a2)k3-4(a2k3- a1dk3-a22a1k) 通过将特征值的实部与虚部分离,得到λk的实部和虚部分别为: (12) (13) 其中j=±1。 因此得到图灵斑图存在的条件为:没有扩散时满足 (14) 可使得特征值都具有负实部,即常微分系统(4)的均匀植被平衡点E2是局部渐近稳定;当加入扩散后满足 (15) 则存在一些k使特征值实部大于0,即扩散系统(3)的均匀植被平衡点E2变得不稳定。因此,当同时满足条件(14)与(15)时,系统发生图灵不稳定性,进而产生图灵斑图。 根据式(12),图1展示了特征方程(10)的特征值实部与对流率a1的色散关系。显然,特征值的实部可以表示为波数k的函数。黑色曲线表示系统无对流项时特征值实部与波数之间的关系,并且随着波数的变化实部均小于零,表明平衡点E*=(s*,v*)是局部渐进稳定的。然而,当固定a2=0.01并使a1逐渐增大时,从3条不同的曲线(绿色、蓝色和红色)可以看出:随着沙的对流率a1增大,对应特征值实部由负变为正,表明了平衡点E*=(s*,v*)由稳定变得不稳定,进一步说明系统(3)出现了Turing失稳现象。 图1 特征方程(10)中特征值实部关于对流率a1的色散关系(h=2.6,vm=15,p=3.83,c=2.97) 对系统(3)展开数值模拟分析。取参数a1=0,a2=0(其他参数详见表1),也就是说,主要模拟系统(3)无对流项时的斑图现象。 表1 植被-沙(V-S)模型中的参数含义及取值 在模拟过程中,设置边界条件为Neumann型,选取200×200的空间格子,空间步长为dx=1,时间步长为dt=0.001,沙与植被的初始分布如下: 其中ξi(i=1,2)是微小的随机扰动项。采用向前差分格式对系统(3)进行数值模拟,直到斑图结构不再发生改变,模拟结束。 当选择参数h=2.56,vm=4,p=3.83,c=2.97,d=0.01时,沙和植被随时间在空间上的分布演化过程如图2、3所示。 图2 沙在不同时刻的斑图结构演化图(其中h=2.56,vm=4,p=3.83,c=2.97,d=0.01) 图3 植被在不同时刻的斑图结构演化图(选取h=2.56,vm=4,p=3.83,c=2.97,d=0.01) 图2展示了沙最终在空间上形成不规则斑纹,且由低体积和高体积沙构成。如图3所示,可观察到植被具有与沙类似的空间演变规律。在阶段性演化过程中,通过比较植被与沙的斑图结构,发现植被密度与沙密度呈正相关。也就是说,如果沙的密度大,植被生物量就会高,这是因为沙是植被生长所需要的基本物质,为植被生长提供所必需的营养和水分。因此,对于相同的沙,体积越大,植物吸收营养的机会越大,植被生物量也会相应增加。 进一步研究植被的内禀增长率h对于植被斑图的影响。接下来,给出不同参数h值对应的植被斑图结构。从图4中观察到:当h从2.56增加到2.8时,即从图4(a)~(c),蓝色区域变小,说明植被平均密度逐渐增大,植被趋于均匀分布。这表明在其他环境条件相同的情况下,植被的内禀增长率越大,植物生长速度越快,相应的植被密度越大。 图4 不同h值下植被斑图结构图(其他参数取值为:vm=4,p=3.83,c=2.97,d=0.01) 通过对比5.1节的模拟结果可以发现,当加入对流项后,植被和沙的斑图结构发生了明显变化,由原来的不规则斑纹(图2与图3)转变成规则的条状斑图(图5与图6)。也就是说,对流是诱导斑图相变的一个主要机制,这对于明确植被斑图产生机制以及斑图如何发生相变非常必要。植被斑图相变可能会导致荒漠化的出现[22],因此本文中发现的沙的对流率可能是植被斑图产生的另外一种机制。 图5 加入对流后,沙在不同时刻的斑图结构演化图(参数选择为:h=2.56,vm=4,p=3.83,c=2.97,d=0.01,a1=10和a2=0.01) 图6 加入对流后,植被在不同时刻斑图结构的演化图(参数选择为:h=2.56,vm=4,p=3.83,c=2.97,d=0.01,a1=10和a2=0.01) 1) 通过数值模拟展示了扩散诱导植被和沙最终形成不规则斑纹,然而沙的对流引起植被和沙最终形成条状斑图结构,表明在沙漠地区盛行风更利于植被形成规则的空间分布结构。 2) 增加植被的内禀增长率有助于植被最终形成空间均匀的分布结构,在现实世界中,如果可以采取一些措施来保护植被,例如,避免过度放牧、随意伐木,植被整体密度会更高。 3) 荒漠化正变得越来越严重,更好地保护环境将有利于植被多样性和沙化土壤稳定性的保持,研究植被-沙模型非常必要且具有现实意义。4 图灵不稳定性
4.1 线性稳定性分析
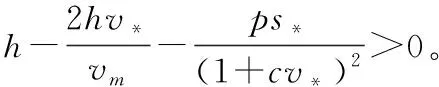
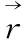
4.2 对流诱导图灵不稳定性
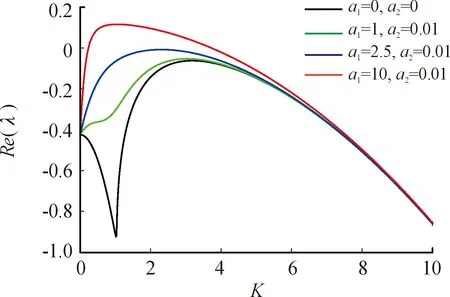
5 数值结果
5.1 扩散诱导的斑图


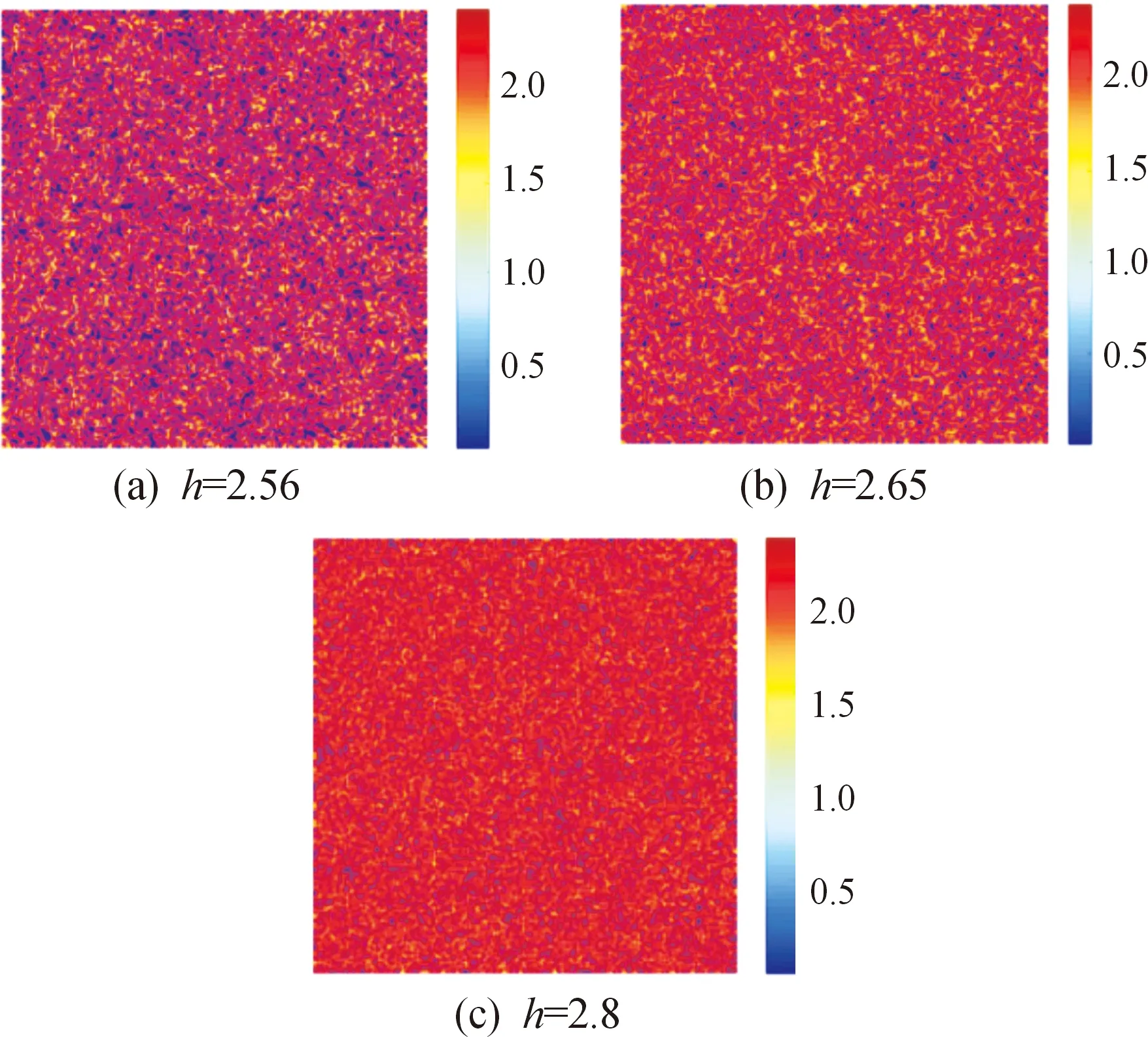
5.2 对流诱导的斑图

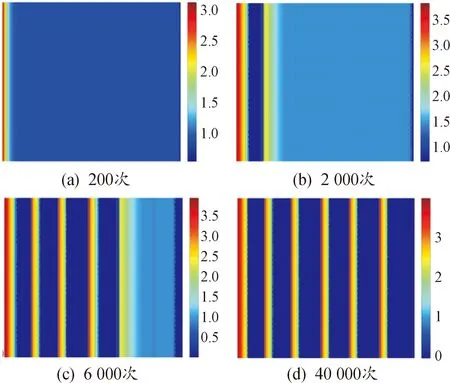
6 结论

