基于驱动因素分解的能源消费预测
——以上海市为例
高 迪,任庚坡,李琦芬,毛俊鹏,桂雄威
(1.上海电力大学, 上海 200090; 2.上海市节能监察中心, 上海 200083)
上海市作为长江流域经济带的骨干和“龙头”,近年来能源需求也不断提高。与日俱增的能源需求,不仅影响我市能源自身安全,而且会对全国能源生产与供给产生一定影响。响应绿色低碳号召,加强自身能源保障,是未来经济社会发展所遵循的规律[1]。因此,把握未来能源需求趋势,对上海市能源战略的制定实施及经济社会持续发展都具有重要意义。
为实现“十三五”时期上海工业绿色发展“双控”目标的完成,本文尝试从工业企业能源消费、工业固定资产投资项目能源消费及产调与技改能耗减少量3部分驱动因素入手调控上海市工业能源消费总量。采用ARIMA-BP神经网络组合模型、情景分析法等能耗预测方法,综合预测上海市工业能源消费总量的需求趋势。
1 样本数据说明
本文研究共涉及7个变量,分别为上海市工业能源消费、经济水平(上海市生产总值)、产业结构(三次产业结构能源消费)、能源强度(单位产值能源消费)、能源消费结构(一次能源消费)、四大高载能行业能源消费以及固定资产投资项目新增能源消费量。考虑数据获得性,本文选取的时间序列跨度为2000—2018年,数据主要来源于历年《上海能源统计年鉴》、《上海统计年鉴》、固定资产投资项目能评管理系统及统计局官网公布信息,数据资料真实可靠,有据可依[2-3]。
2 能源消费预测模型方法概述
目前在能源消费领域预测方法主要有回归分析法、灰色预测法及时间序列法等,常用的能源消费预测方法特点,见表1。

表1 能源消费预测模型特点

续表(表1)
能源消费变化本身会受到很多外部因素的影响,如经济水平(上海市生产总值)、产业结构(三次产业结构能源消费)、能源强度(单位产值能源消费)、能源消费结构(一次能源消费)及固定资产投资项目新增能源消费量等。根据各预测模型的优势比较分析,并结合上海能源消费数据的特点,本文主要采用预测精度较高的时间序列法、人工神经网络法、情景分析法等单一方法构建预测模型,并通过误差绝对值的对比分析,最终确定构建组合模型进行预测,组合预测模型有效提高了单一模型的预测精度,扩大了单一模型适用范围,且涉及参考的因素指标全面新颖、科学合理、方便快捷,适用于上海市工业能源消费预测。
3 分解驱动因素预测能源消费
通过对上海市相关能源消费监测统计部门的调研学习及历年数据整理分析得知:上海市工业能源消费总量主要由3部分构成,即工业企业能源消费量E1、工业固定资产投资项目新增能源消费E2以及通过产业结构调整及节能技改能源消费减少量E3。则可设上海市能源消费总量主要构成关系式:
E=E1+E2-E3
(1)
通过上式可知:将3部分能源消费量通过不同方法逐一进行预测分析,最终将各部分预测值通过式(1)联立即可得出上海市工业能源消费总量的预测结果。其中,预测上海市工业企业能源消费E1采用ARIMA-BP神经网络组合预测模型;预测上海市工业固定资产投资项目新增能源消费E2采用情景分析法;工业产业结构调整及节能技改减少量E3可根据近10年上海市重点用能企业能源审计报告数据统计预算,综合得出上海市工业能源消费总量的预测结果。
3.1 工业企业能源消费E1预测
通过实证分析构建多个单一预测模型进行初步预测,并利用模型组合法提高单一模型精确度,最终作出最优化组合模型对上海市工业企业能源消费E1进行预测。
3.1.1时间序列法——ARIMA预测模型
自回归移动平均模型(ARIMA) 由美国统计学家Box和Jenkins于20世纪70年代提出。ARIMA模型(autoregressive integrated moving average model)被广泛用于时间序列预测分析,其实质是利用差分运算将非平稳时间序列转化为平稳时间序列,再建立ARIMA模型并进行预测分析。在模型ARIMA(p,d,q) 中,p为自回归阶数,d为数据差分次数,q为移动平均阶数[15]。
ARIMA(p,d,q)模型的基本形式如下:
ΔdXt=Φ1ΔdXt-1+Φt-2ΔdXt-2+…+
ΦpΔdXt-p+εt+θ1εt-1+
θ2εt-2+…+θqεt-q
(2)

选取2000—2018年上海市工业能源消费量作为随机时间序列模型的样本数据,将该序列数据导入Eviews 9.0中进行处理,利用ARIMA(p,d,q)模型对上海市工业企业能源消费E1进行预测。
1) 序列平稳性检验
对时间序列进行观察,发现上海市工业能源消费量有明显的波动趋势,为非平稳序列。通过对能源消费量序列进行一阶差分处理,利用 ADF(augment dikey-fuller)方法进行序列的单位根检验,结果见表2。
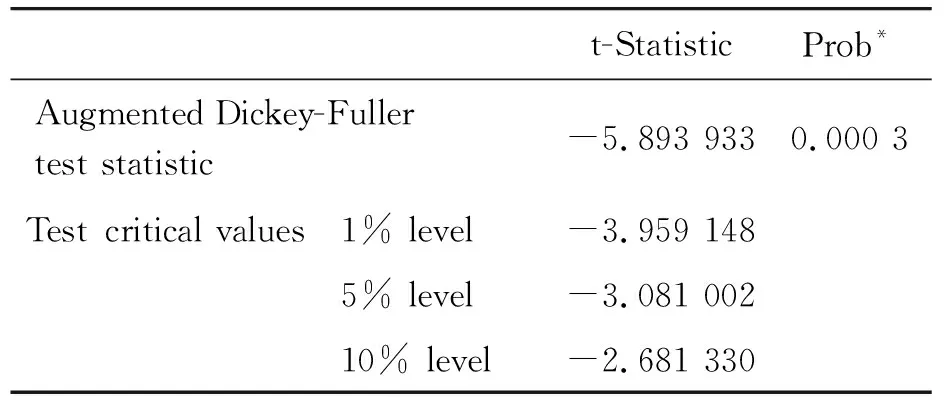
表2 一阶差分序列的ADF检验
单位根检验结果说明非平稳序列经过一阶差分后是平稳的,因此可以对模型定阶为d=1。即对一阶差分以后的平稳序列可以建立 ARMA(p,q)模型。
2) 模型识别与选择
选择AR(p)模型、MA(q)模型还是ARMA(p,q)模型,以及如何确定p、q值,通常利用自相关与偏自相关函数来识别。使用Eviews 9.0统计软件对序列进行自相关和偏自相关分析,结果见图1。
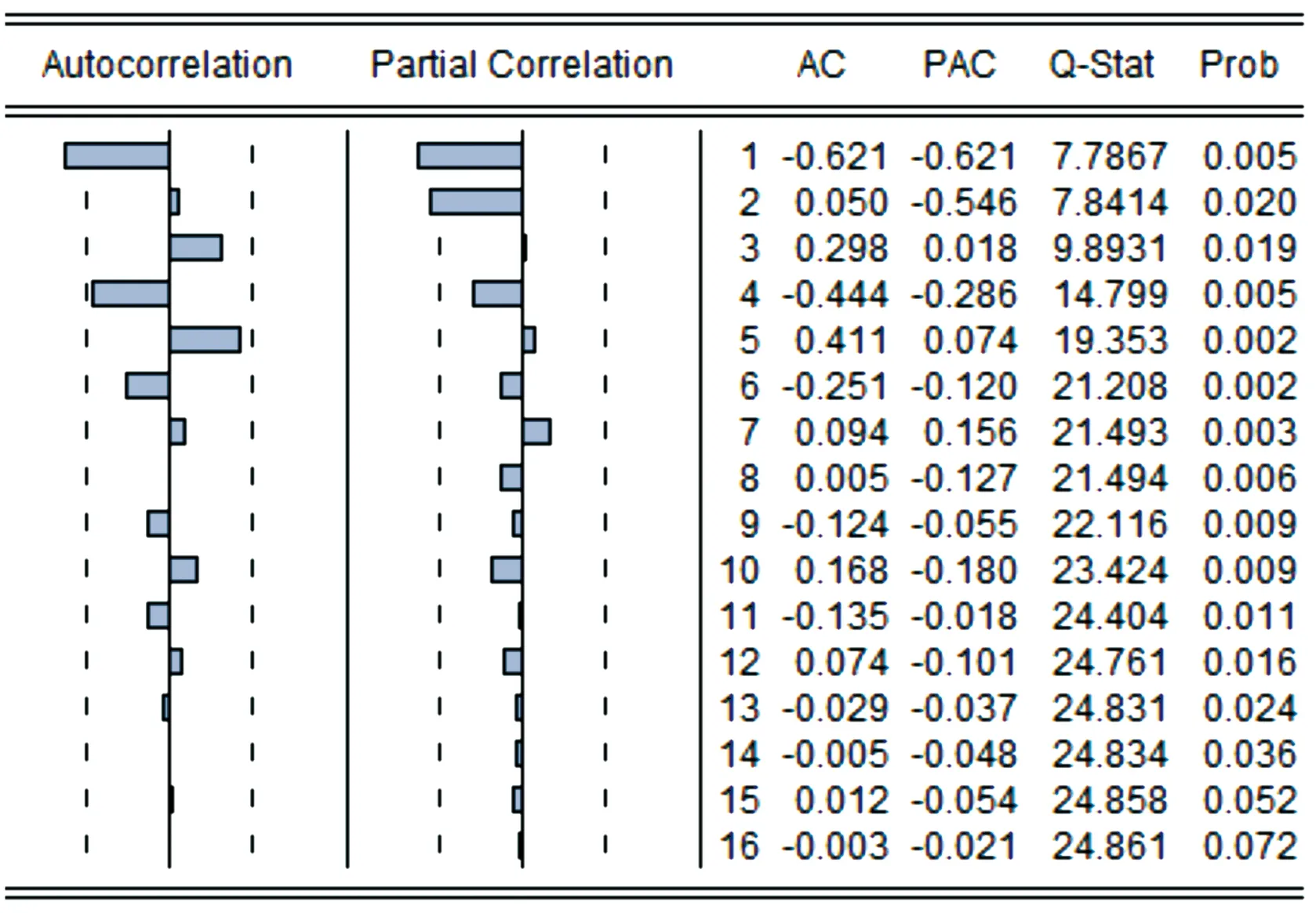
图1 一阶差分序列自相关与偏自相关
在自相关图中,系数显著不为零的阶数为1、4、5;偏自相关图中,系数显著不为零的阶数为1、2。即通过对多个 ARMA(p,q)模型的不断尝试比较,结果显示 ARMA(4,2)模型自回归及移动平均部分系数最为显著,AIC值相对较小,模型拟合效果良好。故可建立上海市工业能源消费的ARIMA(4,1,2)模型,其参数估计结果见表3。
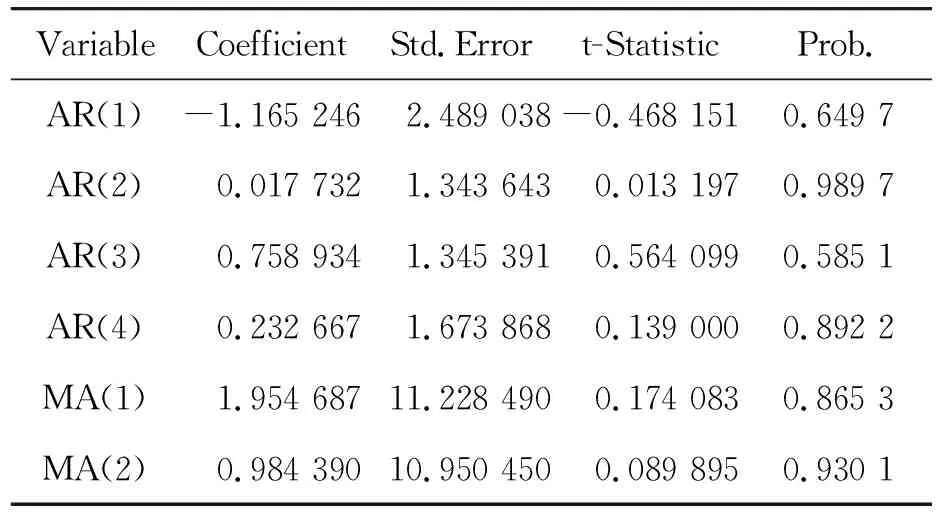
表3 差分序列模型的参数估计
3) 模型预测
运用Eviews9.0软件对ARIMA(4,1,2)模型进行预测,由图2可知模型不确定系数为0.4,即说明上海市工业能源消费ARIMA(4,1,2)预测模型拟合效果较好。

图2 ARIMA(4,1,2)模型估计及预测
根据参数估计结果可得模型的口径为
ΔXt=Φ1ΔXt-1+Φ2ΔXt-2+Φ3ΔXt-3+
Φ4ΔXt-4+εt+θ1εt-1+θ2εt-2
(3)
(1-B)Xt=-1.165 246(1-B)Xt-1+
0.017 732(1-B)Xt-2+
0.758 934(1-B)Xt-3+
0.232 667(1-B)Xt-4+
εt+1.954 687εt-1+
0.984 390εt-2
(4)
根据上式计算出上海市工业企业能源消费ARIMA(4,1,2)模型在2000—2018年中的预测值和相对误差绝对值,见表4。
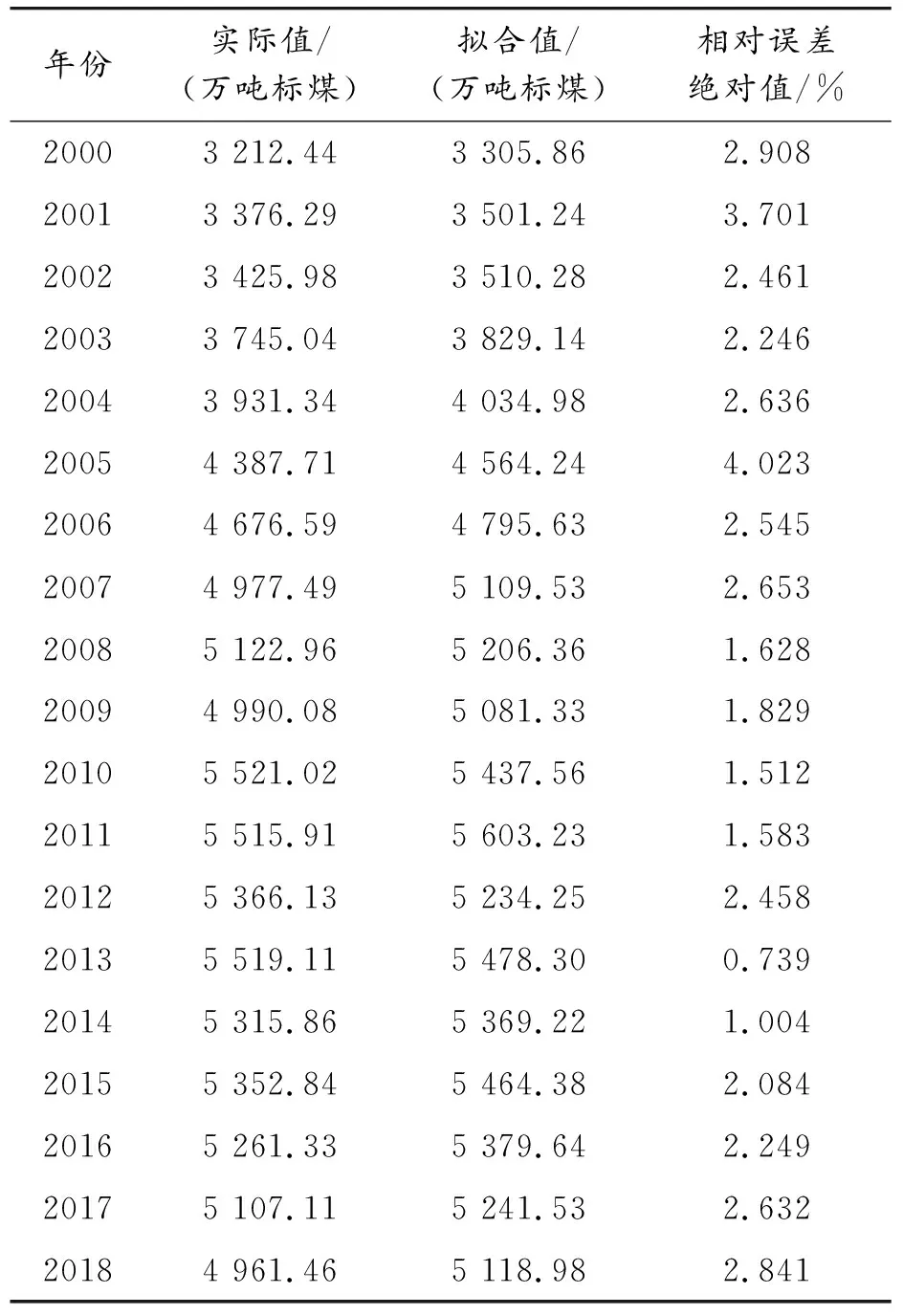
表4 ARIMA(4,1,2)模型能源消费预测
由ARIMA(4,1,2)模型预测结果可以发现:平均相对误差绝对值为2.302%,拟合效果较好,精度较高。
3.1.2BP神经网络预测模型
BP神经网络是指运用误差逆传播(error back propagation)算法训练的多层前馈神经网络,基于梯度下降(gradient descent)策略,以目标的负梯度方向对参数进行调整,是目前为止最成功且应用最广泛的神经网络算法[16]。神经网络由输入层、一个或者多个Sigmoid隐层隐含层和输出层3部分构成,见图3。隐藏层的存在使网络可以呈现和计算更加复杂的关联模式,人工神经网络的基本方法主要由网络训练和测试两部分组成。

图3 BP神经网络预测模型示意图
本文选取2000—2018年上海市工业企业能源消费量作为样本数据,将该序列数据导入Matlab中进行网络训练,利用BP人工神经网络模型对上海市工业企业能源消费进行预测。
建立 BP神经网络模型可分以下几步进行:
1) 归一化处理
归一化处理可避免由于出入向量的物理意义和单位不同对BP神经网络产生影响。将输入数据处理为区间[0,1]之间的数据,釆用公式:
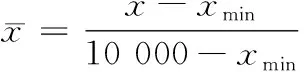
(5)
2) 确定网络层及输入、输出层神经元数
BP神经网络是通过输入层到输出层的计算完成的。网络层数越多需要的训练时间越多,而训练速度可通过增加隐含层节点个数来实现,因此选取含一个隐含层的3层神经网络即可。
输入、输出层神经元数与样本紧密相关,本文利用x(i-1),x(i-2),…,x(i-k)的信息预测i时刻的值,则输出层神经元数为1;通过确定其他参数值,获得输入层神经元数为5,分别为上海市经济水平、产业结构、能源强度、能源结构、四大高载能行业能源消费情况。
3) 确定隐含层神经元数
隐含层中神经元数的确定,关系到模型是否能够有效完成映射。在建模时,首先根据公式初步确定隐含层神经元个数,然后对不同神经元数的网络进行训练对比误差大小来确定隐含层的神经元数。通用的隐含层神经元数的确定经验公式为:
(6)
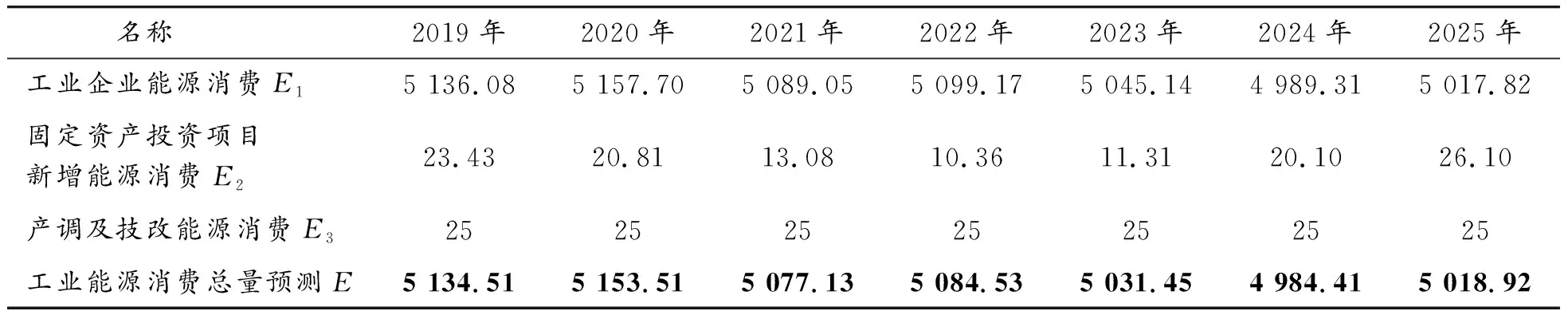
式中:i为隐含层神经元的个数,n为输入层神经元的个数,m为输出层神经元的个数,a为常数且1 表5为选取不同神经元个数时,对应MSE值的变化。从表中可知:最优隐含层神经元数为12个。 表5 不同隐含层赋值时的均方误差 4) 确定传递函数、训练函数 按照BP网络的一般设计准则,由于输入数据已经归一化到[0,1]区间,因此,中间层神经元的传递函数为S型对数函数logsig,而输出层神经元则釆用线性传递函数purelin。训练函数采用常用的Levenberg-Marquardt BP训练函数trainlm。 此时,构成的神经网络如下: net=newff(minmax(训练样本数据),{logsig,purelin},‘trainlm’) 根据构建的BP神经网络在Matlab软件中的循环迭代计算可得2000—2018年上海市工业能源消费的拟合值与相对误差绝对值,见表6。 表6 BP神经网络模型预测 由BP神经网络预测结果表明:平均相对误差绝对值为1.811%,拟合效果较好、精度较高。将2015—2018年上海工业能源消费作为检验数据,运用BP神经网络模型进行预测,其实际值与拟合值,见图4。 图4 Matlab拟合2015—2018年检验数据效果 3.1.3ARIMA-BP神经网络组合预测模型 ARIMA-BP神经网络组合预测模型是将ARIMA模型与BP神经网络模型预测值采用变权重组合法,并根据单一模型各自预测的优点进行互补组合,其精度优于单一预测模型。变权重组合预测法是对较精确的预测值赋予较大的权重,对精度较低的赋予较小的权重。标准差运算公式如下: (7) 其中,ωi为模型i的权重;σi为模型i的预测误差的标准差;n为组合模型的个数。 通过计算得到ARIMA(4,1,2)预测模型的标准差σ1为0.7957%,对应权重ω1=0.486 3;BP神经网络预测模型的标准差σ2为0.753 1%,对应权重ω2=0.513 7。 根据权重建立组合预测模型: Y=ω1y1+ω2y2=0.486 3y1+0.513 7y2 (8) 将ARIMA模型和BP神经网络模型所对应的预测值y1和y2分别代入公式,即可得到ARIMA-BP神经网络组合模型预测值,见表7。 比较表4、6、7可知:采用ARIMA-BP神经网络组合模型预测方法得到的2000—2018年上海工业企业能源消费预测结果的平均相对误差最小。因此,可认为采用ARIMA-BP神经网络组合模型预测结果具有较高的精度,是最为有效的预测方法。 表7 ARIMA-BP神经网络组合模型预测 为了对2019—2025年上海工业企业能源消费趋势进行综合预测,根据组合预测模型,首先采用前面两种单一的预测方法进行预测,再根据各个预测方法的权重值进行加权平均,最终得到综合预测值,见表8。 表8 上海工业企业能源消费综合预测 万吨标准煤 本节利用情景分析法预测固定资产投资项目新增能源消费量E2。采用情景分析方法,根据经验规律等定性分析;定量分析为定性分析提供判据,从定性与定量角度相结合进行预测。 3.2.1定性分析层面 固定资产投资项目能源消费数据具有延迟性特点。例如,2017年投产的“XXX固定资产投资项目”申报预计新增能源消费为10万吨标准煤,该10万吨标准煤能源消费不仅在2017年当年产生,应记为从投产时间起至项目稳定运行年内共产生的新增能源消费。因此,为精准预测未来固定资产投资项目每年的新增能源消费量,需综合考虑固定资产投资项目的投产起始时间、累计年等影响因素,找出内在关联关系规律,根据主观经验并结合定量关系式进行预测。 3.2.2定量分析层面 总结、归纳多年固定资产投资项目能源消费数据特点及规律,因此将固定资产投资项目自投产时间至达到稳定运行年限设置为3年,并结合近3年的扰动因素,设置权重系数分别为0.2、0.5、0.3。如图5所示,即将单一固定资产投资项目新增能源消费自投产年起按20%、50%、30%的比例进行分摊再作累加汇总,进而对未来上海市工业固定资产新增能源消费量进行预测。 图5 情景预测定量分析 由以上方法对2019—2025年上海市工业固定资产投资项目新增能源消费进行预测,结果见表9。 表9 固定资产投资项目新增能源消费预测 万吨标准煤 产调是指调整和优化产业结构,通过淘汰落后产能,增强产业层次和技术水平,进一步提高能源利用效率的过程。 节能技改即为节能技术改造,节能、节水、节材环保及资源综合利用等技术开发、应用及设备制造的鼓励项目,是优化能源结构,促进节能减排,加快建设资源节约型社会的需要。主要节能技术有电机系统节能、工业锅炉窑炉节能、生产工艺改进、能量系统优化、余热余压利用、绿色照明、新能源与可再生能源以及管理节能。 根据近10年上海市重点用能企业能源审计报告统计分析,预计上海市工业产业结构调整每年减少能源消费10万吨标准煤,节能技改项目每年减少能源消费15万吨标准煤,即产调及技改减少能源消费量E3每年约为25万吨标准煤。 综上所述,综合考虑工业企业能源消费、固定资产投资项目新增能源消费以及通过产调技改减少能源消费量的三方面能源消费驱动因素,根据公式 E=E1+E2-E3 (1) 最终确定“十三五”后期及“十四五”全市工业能源消费总量,见表10。 表10 上海市工业能源消费总量预测值 万吨标准煤 根据预测结果,结合历史工业能源消费作时序图。由图6显示,“十三五”后期上海市工业能源消费总量会稍有增长,预测至2020年达到5 153.51万吨标准煤;“十四五”时期将逐年呈下降趋势,但其增速保持稳定,预测至2025年上海市工业能源消费总量为5 018.92万吨标准煤。 图6 上海市工业能源消费总量趋势预测 为完成“十三五”后期及“十四五”时期上海工业绿色发展“双控”目标,有必要准确预测未来几年上海工业能源消费总量。本文综合考虑上海工业能源消费的各方面影响因素,首次以固定资产投资项目及产调技改能源消费角度为预测思路,并利用驱动因素分解的新思想主导全文的预测分析;涉及采用了情景分析预测方法、时间序列预测方法、BP神经网络预测及组合预测共4种预测模型构建上海市能源消费总量预测模型,模型应用多样化,进而得出了“十三五”及“十四五”时期的上海市工业能源消费总量的需求趋势走向。此外,通过对上海市相关能源消费监测统计部门的调研学习,使本文数据资料真实可靠、方法思路有据可依,将理论算法模型与实际应用结合分析,具有一定的实际适用性价值。 预测趋势表明:“十三五”后期上海市工业能源消费呈增长趋势,但增速较为平缓;进入“十四五”时期,由于上海能源形势的转变及产业结构不断优化等多方面因素,预测上海工业能源消费将进一步放缓。预测结果显示:利用驱动因素分解构建的组合模型影响因素考虑全面,相对误差小具有较高的精度,适用于上海市工业能源消费预测。因此,本文预测方法也为能源消费需求预测以及理论预测方法的改进提供了一种新的思路,具有相对的合理性及良好的可推广性。
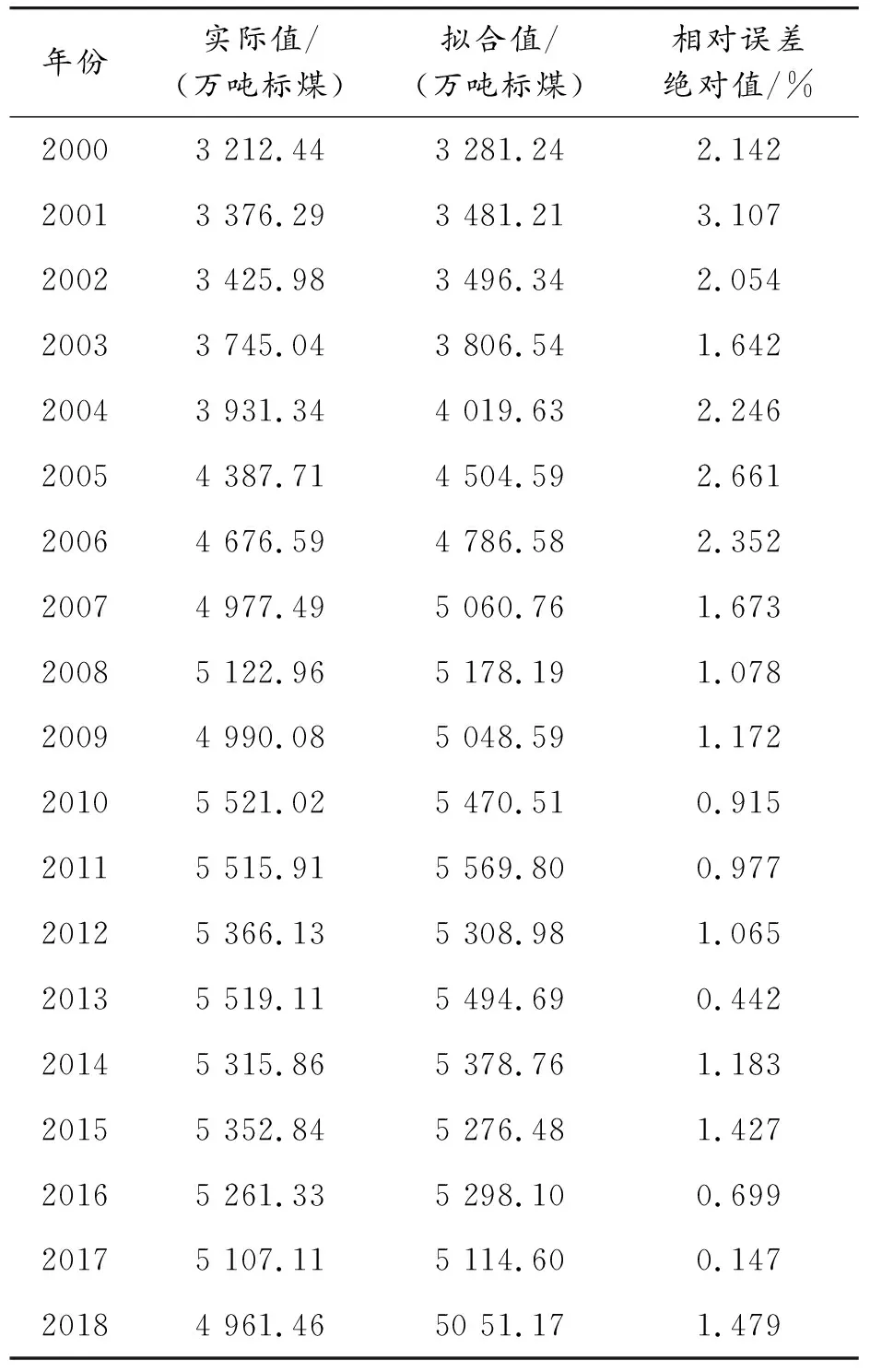


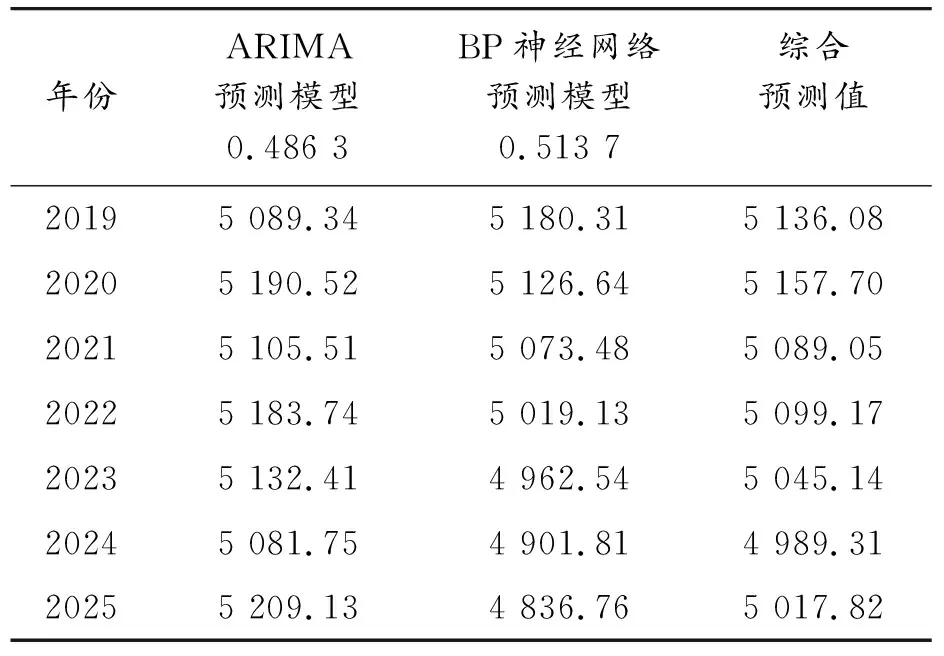
3.2 工业固定资产投资项目能源消费E2预测
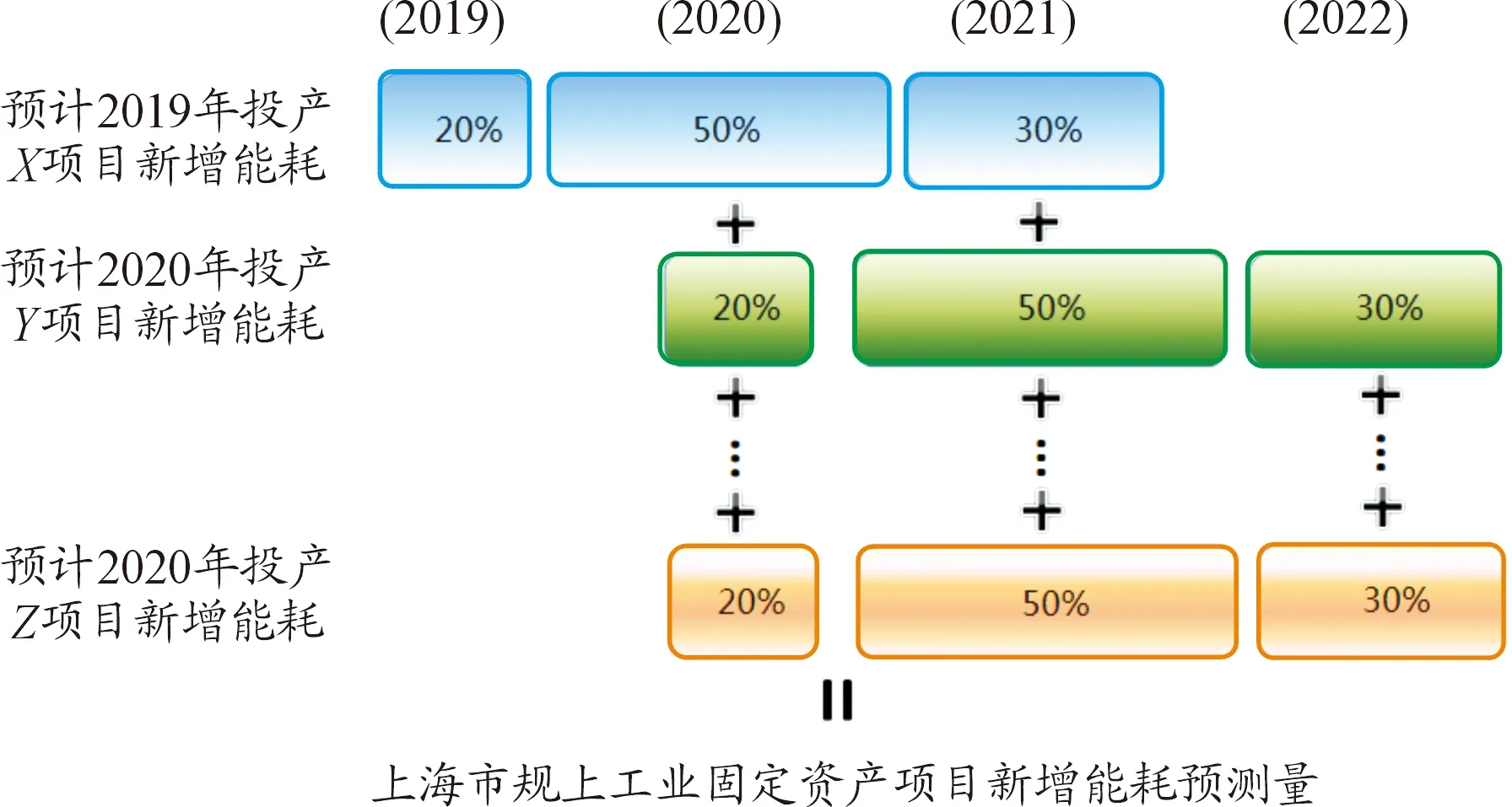

3.3 产调及节能技改能源消费E3预测

4 结论

