基于学习观支持的数学实验教学实践理路

孙朝仁 朱桂凤

摘   要

以“做数学活动”为载体，通过“实践中学、向实践学、再实践学”频道的确立，构建数学化要素关系分布图，展现“数学化学习观”支持的数学实验教学的实践理路。

关键词

学习观  数学实验  课堂变革

学习观是一种形而上思想，由来已久。其中，“学”涵盖学会、学好、学有所乐等本体论思想;“习”涵盖练习、习得、习有所值等实践论行为。从认知心理学看，学习观是人们在认知过程中对知识理解，知识的获得、保持与迁移以及知识变换等知识价值认同程度的一种客观反映。在数学实验教学论范畴，学习观包括在实践中学习“个体经验”、向实践学习“事实经验”和在实践中向实践学习“客观经验”并“理性调用”，涉及将“具体”上升为“抽象”，将“感性”上升为“理性”，将“特殊”上升为“一般”。

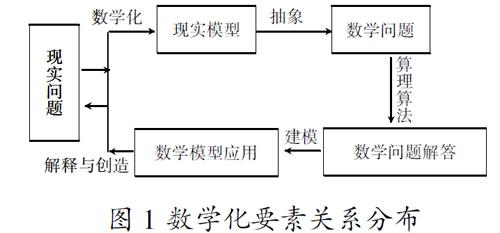
本文以“做数学活动”为载体，通过实践中学、向实践学、再实践学频道的确立，构建数学化要素及其关系的分布，展现“数学化学习观”支持的数学实验教学的实践理路（如图1）。突出抽象、推理、建模三大能力的提升，关注“学”“学好”“学得温情”“学得有滋有味”等课堂变革目标的进一步实现。

图1 数学化要素关系分布

一、确立“实践中学”频道，将具体上升为抽象

数学实验作为课堂变革的一种方式，为数学理解做出了不可替代的贡献。确立“实践中学”的频道，就是建立“生活与数学”同行频道，让学生在实践中经历横向数学化（生活→数学）和纵向数学化（数学→数学）过程。换句话说，就是让学生在做中和思考中，将实践具体转化为数学抽象，提高用数学的眼光观察现实世界的水平。《义务教育数学课程标准（2011年版）》开宗明义：“使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程。”这就要求学生像数学家那样，经历概念的发生、发展过程或经历再创造过程，即“了解一种理论的最好方法是找出研究那種理论原型的具体例子”。这里的“找出”意味着从具体活动中抽象出一类事物的规律（或数学关系），获得个体经验。因此，将具体上升为抽象，需要关注两个方面。

1.横向数学化实践

让学生在横向数学化实践中，将生活具体转化为数学具体，让人人可学成为现实。在数学实验教学论范畴，横向数学化就是将生活问题转化为数学问题。譬如，让学生经历“打印纸中的数学”做、思考的体验过程，可以将看不见的无理数概念显化为具体的、看得见的概念对象，这就是一种“生活→数学”的经典实践样例。具体操作过程涵盖三个思维层次：从认知需要层次看，让学生将A型纸的代表A4纸的短边有序叠合在长边上，构造正方形（生活具体）;从审美需要看，再将构造的正方形的对角线有序叠合在长边上（数学具体）;从自我实现的需要看，经过观察和过滤登记，发现正方形的对角线与A4纸的长边完全叠合，由此得知，A4纸的长边与短边的比值为■（生活具体→数学具体）。这种直观基础上的可视化认知过程符合初中学生“形象思维>抽象思维”的认知心理水平，是横向数学化常见的实践样例。当然，将生活问题转化为数学问题需要做与思考，更需要洞察与表征，方能将生活具体上升为数学具体，实现人人学好。有专家指出，“实验数学是这样的一个数学分支，它通过对猜想和非形式化的信念的实验探索，以及对此过程中所获信息的仔细分析，最终对数学界提出的各种洞察到的事物加以组织、分类和传播”[2]。其中，洞察→组织→传播的过程，就是一种“生活具体”到“数学具体”的过程，是一种“能学好”学习观，不止于知识、方法，还在于关注人的成长需要，反映实验育人的正确态度。

2.纵向数学化实践

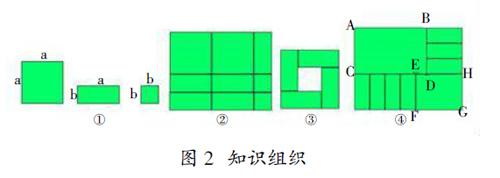
让学生在纵向数学化实践中，将数学具体转化为数学一般，让不同发展变得可能。就认知心理学看，纵向数学化就是让学生在问题解决中，将具体的一类问题（数学具体），转化为结构化的一般问题（数学一般），突出深度学习的特征（思维的高投入），落实不同人在数学上获得不同的数学发展目标。譬如，图2的设计与呈现，就突出数学具体到数学一般的认知心理倾向。在变量思维的参与下，将直观分析、综合比较、抽象概括融于一体，建立一种稳定的结构，可变的字母，这就是数学化。其中，问题（1）是将图形语言转换为符号语言，是数学具体上升为数学一般的实践清样;问题（2）是代数关系的内部建立，是纵向数学化的初级阶段;问题（3）是变量思维与定值关系的构建。具体实施过程，包括拼图算图，整体局部哲学视角，算法算理以及抽象表征等高投入思维。即在图2②中，局部思想的结果描述是2a2+5ab+2b2，整体思想的结果描述是（2a+b）（a+2b），由此不难获得一般化的结论2a2+5ab+2b2=（2a+b）（a+2b）;在图2③中，从整体看，阴影部分的面积可以描述为（a+b）2-（a-b）2，从局部看，阴影部分的面积为4ab，因此有（a+b）2-（a-b）2=4ab的关系产生，在图2④中，S四边形ABCD+AB·3b，S四边形EFGH=a（AB+a-4b），根据定值思想，不难确立a=3b。这就是纵向数学化全景展示的一个好例子，是不同学生获得不同发展的好载体。

二、构建“向实践学”频道，将感性上升为理性

“向实践学”是人类获得数学知识的一般方法。数学基本事实、数学公理体系、数学概念及其要素的恰当呈现，都是向实践学的思维产物。在做数学活动范畴，构建“向实践学”的频道，就是让学生在做数学中学习做数学。包括“数学过程和基于过程的数学基本能力、数学内容和数学情境”[3]等PISA描述的核心素养目标。其中，数学过程应当包括三个阶段：知识是怎么来的、知识是什么、知识是怎么去的。回答好数学过程及其相关问题，就是做好数学的最正确学习观，即知识来自于实践，是向实践学的产物;知识是将实践感性转化为实践理性;知识要将个体经验上升为事实经验。同时，基于数学过程的能力主要是抽象、推理和建模三大能力的针对性培养，数学内容和数学情境是“做数学”的两个方面，前者是将知识结构转化为认知结构，后者是构造向实践学的组块，让不同人学不同的知识，获得不同的发展。其理论依据是“个体发展过程是群体发展过程的重现”[4]。为此，在做中学，将实践感性上升为实践理性，需要做好两个方面的工作。

1.做数学

通过“做”，让学生经历具体到抽象的不同层次，即情境层次、指涉层次（提到、涉及、再生）、普遍层次、形式层次，掌握不同的知识体系，并将个体经验转化为事实经验。譬如，让学生用1号（a×a型）、2号（a×b型）、3号（b×b型）纸片拼图，在局部与整体哲学思想的指导下，研究因式分解发生过程的合情、合理、合目的性，就是通过做中学，让学生经历“具体”到“抽象”的不同层次，实现将“个体经验”及时上升到“事实经验”的理性水平。具体来说，可设置问题（1）让学生用1张1号纸片和2张2号纸片拼长方形，在两种算法的参与下，可以获得用“提公因式法”分解因式的一般方法，即a2+2ab=a（a+2b）;问题（2）让学生用1张1号纸片、2张2号纸片和1张3号纸片拼正方形，在两种算法的参与下，可以获得用“完全平方公式”分解因式的一般方法，即a2+2ab+b2=（a+b）2;问题（3）让学生用1张3号纸片，完全覆盖在1张1号纸片上（设定1号纸片规格远远大于3号纸片规格），在裁剪、拼接、算理、算法思维配合下，可以获得用“平方差公式”分解因式的一般方法，即a2-b2=（a+b）（a-b）。如果说，拼图、覆盖、裁剪、拼接、算圖（情境层次）是做中学的表现，那么概念关系、代数关系的建立则是具体到抽象的产物（指涉层次和普遍层次），而一提、二套、三分解（形式层次）基本方法的表征是将个体经验上升为事实经验的实践清样。这些做数学过程中的抽象层次，为“学”不同知识铺设了经验，促进了学的合情、合理、合目的性。

2.用数学

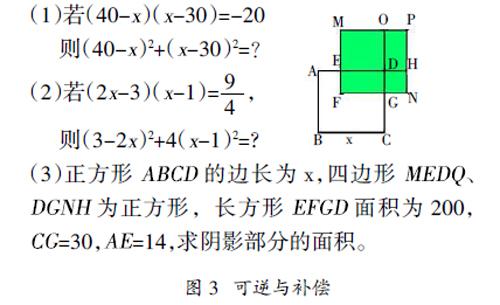
通过“用”，让学生经历感性到理性的不同阶段，即直观阶段、分析阶段、抽象阶段、演绎阶段（算理算法等非完全运演、直观运演）、严谨阶段，实现不同的发展目标，并将结构知识转化为认知结构。譬如，图3旨在让学生通过用数学，经历感性到理性的不同认知阶段，落实不同发展目标的可行性，并促进“结构知识”到“认知结构”的转换。具体操作过程如下：问题（1）旨在让学生用a2+b2=（a+b）2-2ab这一数学结论，在整体思维或换元思想的参与下，获得（40-x）2+（x-30）2的解决方案;问题（2）旨在让学生通过化归转化方法、整体思想、偶数形式服从奇数形式的思想指导，构造可求解的非完全演绎推理;问题（3）旨在让学生通过结构化问题（类问题）解决，实现将知识结构转化为认知结构。如果说问题（1）（2）是用概念，问题（3）则是将实践感性上升为实践理性的具体表现。其中，问题（1）是理性基础上的直观阶段，问题（2）是算理指导下的分析阶段，问题（3）是抽象、运演和严谨阶段，是用好数学的表现。图3有助于不同发展目标的实现，是人人学好结构数学的好载体，是培养学生用数学思维思考数学世界的好例子。

三、开辟“再实践学”频道，将特殊上升为一般

数学学习观是人们对数学本体价值的认识，是一个人的数学世界观和方法论体系的复合物，是对数学和数学任务采用何种方法解决的观念。那种只为得个答案的学习观是需要叫停的，因为去反思化的问题解决屏蔽了知识获得背后人的成长机制。“再实践学”是一种数学实践论和本体论的融合产物，是一种理论联系实际的学习观，是学生学好数学绕不开的路径，是数学地组织数学世界的过程。在做数学活动范畴，举一反三是再实践学的常见思维方式，元认知监控是再做数学的学科育人抓手，是有用组合建立的“导航仪”，是培养学生数学创造的有效途径。开辟“再实践学”的频道，就是对教育不是往行李箱里塞满物品过程的认同，是让学生像数学家那样经历知识的再发现过程、再表征过程和再描述过程，在反问监控和元认知体验的心理前提下，建立工具性理解到关系性理解的思维桥梁。用通俗易懂的话说，就是通过做中反思、反思中再做，将实践特殊上升为实践一般，并以此为基础将事实经验上升为客观经验。为此，通过开辟再实践学的频道，将实践特殊上升为实践一般需要突出关注两个方面，方能将知识转化为能力，将经验转化为方法，将素养转化为人的成长及学习力。

1.直觉的选择性

关注直觉的选择性，驱动有用组合的发生，将事实经验上升为客观经验，让学生获得能力的同时知其所以然。譬如，图4旨在让学生体验做图的过程，积累活动经验，经历直觉的选择与登记，引动有用组合的发生。具体做数学的过程如下：在图4①②中，依据两种算法，直观写出事实经验层面的结论，即（a+b）（a+2b）=a2+3ab+2b2或a2+3ab+2b2=（a+b）（a+2b）、（a+b+c）2=a2+b2+c2+2ab+2ac+2bc或a2+b2+c2+2ab+2ac+2bc=（a+b+c）2;问题（2）的解决突出有用组合的发生，在“用结论”条件下，可知a2+b2+c2=112-2×38=45;问题（3）旨在让学生体验“画”的过程（见图4④），并将画的直觉选择转化为符号意识，即2a2+5ab+2b2=（a+2b）（2a+b）数学结构产生式产生，突出建模“建”的过程和“建”的作用。乔治·波利亚将做的过程描述为三个阶段：探索阶段（接近于学生的行动和感受）、形式化阶段（引入了具体概念，并上升为概念化水平）和同化阶段（洞察事物内部属性）。问题（1）是探索阶段，应该反映直觉的选择性;问题（2）是形式化阶段，投射了有用组合的发生;问题（3）是同化阶段，是将事实经验上升为客观经验的好问题。如果说，做图是直觉洞察代数关系的客观经验，类结构思想是知其所以然，那么理解则是学生学好数学的表现。

2.建模的逻辑性

关注建模的逻辑性，驱动反问监控，将工具性理解（特殊）上升为关系性理解（一般），让学生学会表达的同时提升现实问题解决水平。譬如，在图1中数学化要素的分布与构建就在一定层面反映建模过程的逻辑性，带有抽象→建模→用模→解模的一般逻辑过程特征。其中，反问监控需承担这样的任务，即：这类问题属于哪个领域？（“数与代数、图形与几何、统计与概率”领域的，还是“综合与实践”领域的。）需要用怎样的类结构（模型）去研究？（方程模型、函数模型、不等式模型、综合模型、数据分析模型、非标准模型、超回归模型及各模型内部要素和要素关系等。）“你是怎么想到的？还有没有更好的方法？下一步该怎么思考？”等等。这些反问、问中之问、逐级逐层的“内问”，是数学特殊上升为数学一般必经思维之途，是数学地表达数学世界的产物。图4反映代数建模的逻辑过程、图3属于模型的应用与拓展、图2是代数倾向特征鲜明的综合模型的再现。需要指出的是，图1中的“现实问题→现实模型”[5]属于工具性理解的常见信息组合与加工方式，图1中的“数学模型→数学问题解答→数学模型应用”属于关系性理解的一般思维方式。这些逻辑思考方式的建立、研究与定位是提升学生解决现实问题的“法宝”，是做数学的理性价值和支持学习观的根基，是数学关键能力培养的思维通道。

参考文献

[1] 张玉峰，智红燕，付夕联.数学直觉的作用[J].数学教育学报，2017（01）：82-87.

[2] 王萍.“数学实验”活动是促进学生参与教学的一种有利形式[J].天津师范大学学报：基础教育版，2002（12）：29-31.

[3] 曹一鸣，朱忠明.变与不变：PISA2000—2021数学测评框架的沿革[J].数学教育学报，2019（04）：1-5.

[4] 岳欣云，董宏建.数学教育“生活化”还是“数学化”——基于数学教育哲学的思考[J].教育学报，2017，13（03）：41-47.

[5] 黄健，鲁小莉，王鸯雨，徐斌艳.20世纪以来中国数学课程标准中数学建模内涵的发展[J].数学教育学报，2019（03）：18-23.

【责任编辑  郭振玲】