无叶片风力机变固有频率系统的涡激摆动特性及捕能效率

龚曙光， 吴兴豪， 谢桂兰， 张建平

(湘潭大学 机械工程学院， 湖南 湘潭 411105)

无叶片风力机的物理模型，如图1所示。当风作用在其捕能柱时，涡激作用力使捕能柱在横向和流向产生强烈的周期性摆动，再通过其能量转换装置将摆动机械能转换成电能。特别是当捕能柱横向摆动的固有频率与涡激频率接近时即出现“锁频”，捕能柱将产生共振，即捕能柱能获得最大的振幅，从而就可捕获最大的风能[1]。

图1 无叶片风力机物理模型

同时在捕能柱的下端连接一个由永磁体构成的回复力装置，它既可控制捕能柱在共振时其振幅的无限增大，不至于给捕能柱结构带来破坏，也可给捕能柱一个回复力，将有利于捕能柱的摆动。

针对涡激振动的发电装置，国内外学者已开展了相关的试验和理论研究，如Bernitsas等[2]利用涡激振动水生洁净能源(vortex induced vibration aquatic clean energy，VIVACE)装置将水流动能转换为电能，实现了水力涡激平动能量的提取。Lee等[3]研究了雷诺数和系统阻尼等参数对VIVACE装置转换功率的影响，指出在涡激振动上部分支柱体振幅比随雷诺数的增大而增大，且随系统阻尼的增大而减小。罗竹梅等[4]通过对水流涡激振动的数值模拟，发现选取适当的折合速度和质量阻尼比可使捕能效率最大化，等等。然而目前大部分研究均是针对柱体在水流涡激平行振动下进行。

也有学者针对回复力矩开展了相关的研究，如Mackowski等[5]对涡激平动非线性回复力系统进行了研究，并指出非线性回复力系统对柱体高振幅、高功率的雷诺数范围产生了较大的影响；Barton等[6]研究了一种基于永磁体的非线性回复力能量收集装置，从而使得该装置在更宽的频率范围内具有高功率特性；Gammaitoni等[7]研究了非线性回复力系统对振动压电能收集装置性能的影响。同时，Yazdi[8]研究了无叶片风力机的一种固有频率控制器，其结果表明改变系统固有频率对无叶片风力机的输出功率影响很大等。

目前针对涡激振动发电装置主要以水作为流体介质，且基本以柱体涡激平行振动的研究为主，同时回复力矩对风致涡激摆动的影响研究也非常缺乏，因此本文基于计算流体动力学(computational fluid dynamics, CFD)-刚体动力学(rigid body dynamics, RBD)的耦合方法，建立无叶片风力机捕能柱的三维涡激摆动模型，对非线性回复力矩系统下的涡激摆动特性及能量捕获效率进行研究，所得结果将为无叶片风力机的设计提供指导。

1 模型简化与理论推导

1.1 横向摆动的简化模型

从图1可知，其捕能柱除要受到涡激作用产生的气动升力Fl和气动阻力Fd之外，还受到永磁体作用力、阻尼作用力以及自身重力的作用。其中永磁体为捕能柱涡激摆动提供回复力矩，但产生的回复力矩随捕能柱摆动角度的变化呈非线性关系[9]，但在摆动角度较少时，回复力矩与摆动角度之间近似为线性关系。因此本文首先对永磁体产生作用的力矩进行线性化分析，即将整个装置视为质量-弹簧-阻尼系统，然后再对回复力矩与摆动角度之间的非线性关系进行研究。

若将捕能柱底面中心视为摆动中心，则其在涡激作用力下的摆动模型可简化，如图2所示。

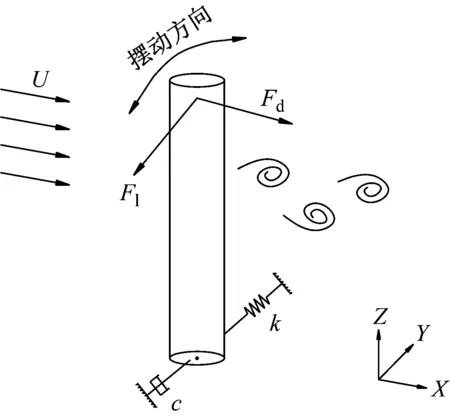
图2 捕能柱摆动模型

对于在线性回复力矩作用下的捕能系统，其捕能柱双自由度刚性涡激摆动的动力学响应方程可表示为

(1)

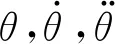
捕能柱在任意位置受到其自身重力矩与摆动角度有关，且重力作用力矩可表示为

(2)

式中：mg为捕能柱自身重力；L为捕能柱质心到摆动中心的高度。

当捕能柱不受风力作用时，由式(1)和式(2)可得柱体单方向摆动的控制方程为

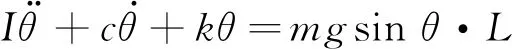
(3)

因式(3)无通解，须对该摆动系统的固有频率做进一步分析，但当柱体摆动幅度较小时即(θ≤0.087 5 rad)，有sinθ≈θ，则由式(3)可得

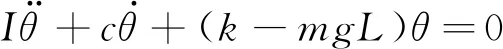
(4)

且式(4)的特征值为

(5)

式中，ω为该振动系统的固有圆频率。

则图2所示刚性振动系统固有频率fn的计算式可表示为

(6)

即图2所示简化模型的固有频率fn与捕能柱质量m、系统阻尼系数c、回复力矩系数k以及质心位置L相关，且在摆动过程中保持不变。

1.2 变固有频率系统分析

因永磁体构建的回复力装置，其产生的回复力矩随捕能柱摆动角度的变化呈非线性关系，且在一定摆动角度内可拟合成二次函数。而在Yazdi对回复力系统的研究指出，可通过改变永磁体结构的参数值来得到涡激平动所需要的线性或非线性回复力。因此本文将根据已有的永磁体结构参数，构建线性回复力函数和两种二次回复力函数，以探讨其对捕能柱涡激摆动特性及能量捕获效率的影响，从而为无叶片风力机永磁体结构的设计提供指导。

假定捕能柱采用ABS(Acrylonitrile Butadiene Styrene)塑料薄壁圆柱结构，其材料密度为1 020 kg/m3，选取柱体外直径D=0.1 m，长径比L/D=5，壁厚1 mm，系统质量阻尼比为0.33，设置永磁体回复力矩装置的线性刚度系数为k=25.63 N·m/rad，由此构建回复力矩与摆动角度之间的线性函数与两种二次函数表示为

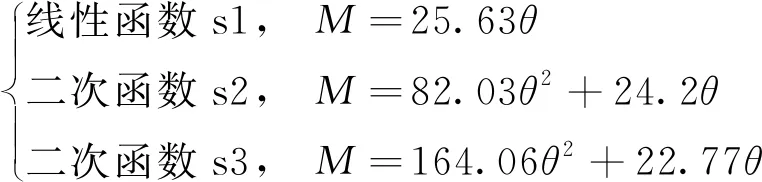
(7)

由式(7)可知，当3种函数关系在摆动角度为θ=0.017 5 rad(即1°)时具有相同的回复力矩，而当θ=0.034 9 rad(即2°)时函数关系s2与函数关系s3分别大于函数关系s1的回复力矩0.05 N·m和0.1 N·m。

3种函数关系在不同摆动角度时回复力矩的变化曲线，如图3所示。

从图3可知，对具有非线性回复力矩的捕能系统来说，当摆动角度在区间[θ，θ+Δθ]内变化时，可近似采用线性函数来表示，即有

(8)

这意味着此时回复力矩的刚度系数k与θ相关，由此可定义非线性回复力矩系统在某一摆动角度下的固有频率为

(9)

由式(9)可知，在涡激摆动过程中，对具有非线性回复力矩的捕能系统，其固有频率与摆动角度下回复力矩函数的斜率相关，即非线性回复力矩函数的斜率控制着捕能系统在某个角度下的固有频率。

结合式(9)和图3可知，对具有线性回复力矩的捕能系统来说，其固有频率在涡激摆动过程中保持不变。而对具有非线性回复力矩的捕能系统来说，其固有频率随摆动角度的增大而逐渐增大，且非线性化程度越高固有频率增长速率越快，即非线性回复力矩捕能系统的固有频率会随摆动角度的变化而发生改变，因此本文定义其为变固有频率系统。

在摆动角度小于0.017 5 rad时，3种函数的斜率发生了切换，即其系统的固有频率值也将发生切换(见图3(b))。

(a) 回复力矩与摆动角度的关系

1.3 能量捕获效率

在捕能柱涡激摆动过程中，风力对柱体所做的功可由升力矩M(t)与柱体摆动角速度的乘积得到，即

(10)

则捕能柱在T时间内通过涡激摆动捕获风能的功率可表示为

(11)

风力场中蕴含的功率用流体产生的动压与容积流量的乘积表示为

Pfluid=PTQ

(12)

式中：PT为流体动压；Q为流体容积流量，分别表示为

(13)

Q=AU

(14)

式中：ρ为风的密度；U为风速；A为迎风面积，且有A=DH，其中D为柱体外直径，H为柱体高度。

则风力对圆柱体所做的总功率可表示为

(15)

由式(11)和式(15)得到时间T内捕能柱产生的能量捕获效率为

(16)

采用数值积分得到式(16)的离散形式

(17)

式中，Δt为数值计算的时间步长。

2 数值计算方法及模型验证

2.1 数值计算方法

采用CFD软件Fluent进行数值计算，柱体在不同时刻所受到的磁性回复力矩、阻尼力矩和重力力矩通过UDF(user defined function)程序控制。柱体在任意时刻受到的总力矩为风力与重力对柱体产生的力矩矢量和再减去该时刻柱体受到的磁性回复力矩与阻尼力矩。

本文采用六自由度动网格模型求解，动网格的更新采用整体动网格法，即将流体域所有网格均设置为随柱体振动的随动网格，同时将风力入口面速度方向设置为固定不变的来流方向。在其流固耦合计算中，首先得到柱体结构的压力场，再通过UDF得到捕能柱所受的总力矩，通过求解柱体摆动的角速度及角加速度，进而得到柱体在每个时间步长内的摆动角度。在完成每个时间步长的计算后再进行网格更新，然后进行下一个时间步的计算，如此循环下去。边界条件及网络模型如图4所示。

按照前述捕能柱的结构参数，设置流体域宽度和长度大小为20D×30D；流体入口面设置为速度入口；流体出口面设置为压力出口，相对压力取为0；上、下、左、右面均设置为对称边界条件(见图4(a))。

基于雷诺平均Navier-Stokes方程，采用SSTk-ω湍流模型求解。柱体壁面第一层网格按照y+～1的要求进行划分，近壁面网格径向延伸率设置为1.08，径向10D内作为O型网格核心加密区，最大网格尺寸不超过0.1D；柱体高度方向网格尺寸参考文献[10]给出的公式N=10L/D进行划分，其中N为柱体高度方向节点数，计算网格模型见图4(b)。

(a) 边界条件

2.2 模型验证

本文计算雷诺数Re范围为Re=1×104～ 3×104。为验证本文所构建模型的可行性，在雷诺数分别为Re=2×104,Re=3×104时，将柱体静止绕流模型所得结果与文献结果进行了对比分析。其中，时均阻力系数定义为Cd=2Fd/ρU2D(Fd为捕能柱所受到的时均阻力)；斯特劳哈尔数定义为St=fD/U(f为旋涡脱落频率)，通过数值仿真计算，所得结果如图5所示。

从图5可知，在亚临界雷诺数区间内，本文数值模拟所得到的时均阻力系数Cd和与Achenbach[11]的和Wieselsberger[12]的试验结果符合程度较好，而斯特劳哈尔数St与Norberg[13]的试验结果较为接近，这说明本文所建立的数值模型是可行的。

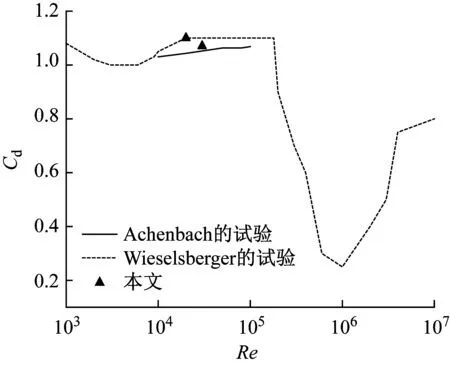
(a) 时均阻力系数Cd与Achenbach和Wieselsberger的试验对比

3 数值模拟结果及分析

下面将针对式(7)所示3种回复力矩函数所构建的变固有频率系统，探讨其对捕能柱涡激横向摆动特性的影响。

3.1 对横向摆动角度的影响

不同捕能系统横向摆动角度随风速的变化曲线，如图6所示。在涡激平动中，常用折合速度Ur=U/fnD取代实际流速，但由于变固有频率系统fn为非恒定值，本文未作风速的无量纲化。

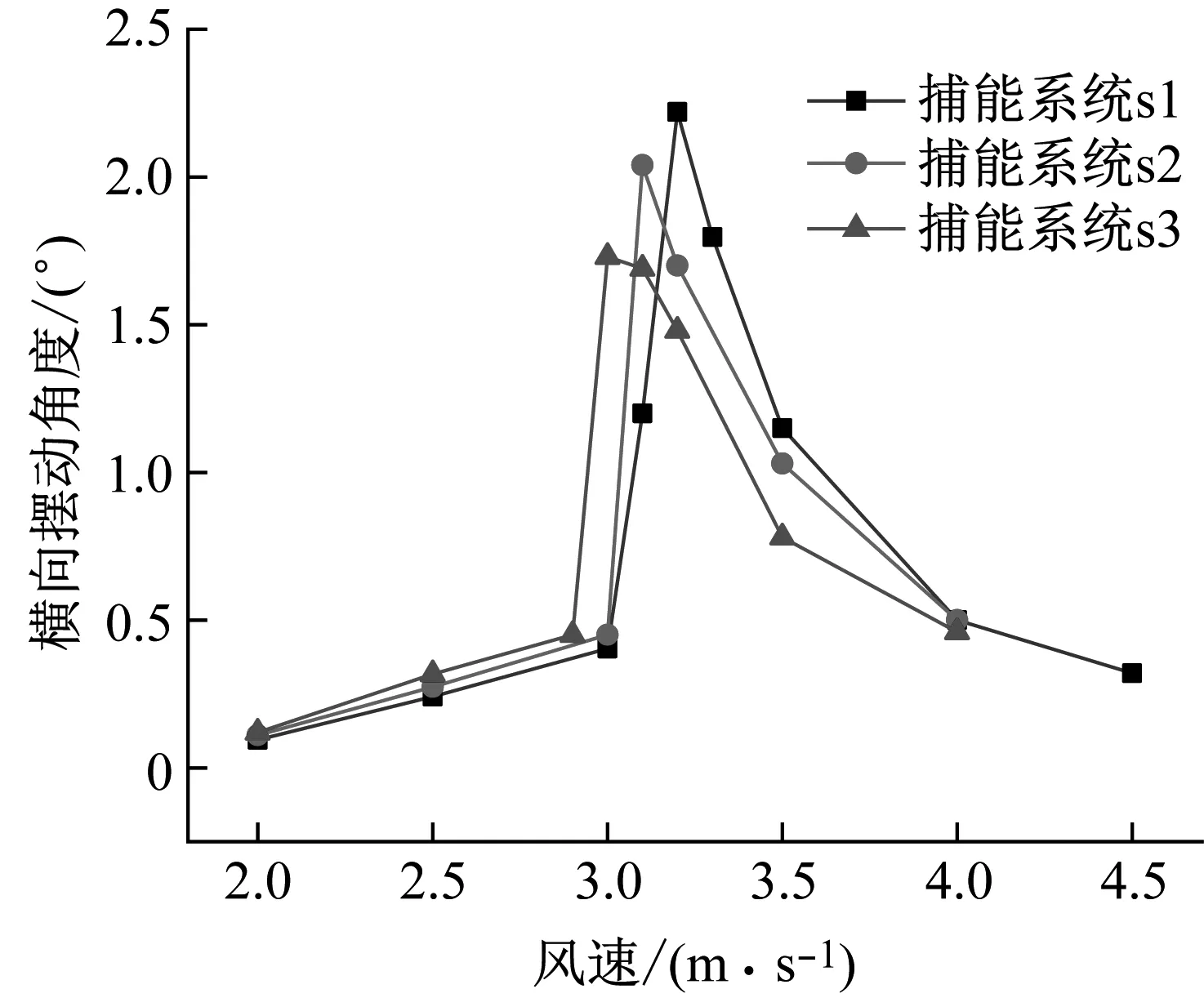
图6 捕能系统横向摆动角度随风速的变化

从图6可知，3种捕能系统在横向的摆动角度峰值随回复力矩非线性化程度的增加呈递减趋势，且横向摆动角度峰值对应的风速向前推移。这是由于具有函数s2和s3的捕能系统，其固有频率初值要小于具有函数s1的捕能系统，因此使得具有非线性程度高的捕能系统在较小风速下就进入了频率“锁定”状态，这与Mackowski等对涡激平动试验研究所得结论相似。同时当摆动角度大于1°后，二次函数s2和s3的回复力矩逐渐增大，从而也对捕能柱横向摆动角度的增大起到了抑制作用，这意味着非线性回复力矩越小越好。

从图6也可知，具有函数s1与s2的捕能系统，其“锁频”区间要低于具有函数s3的捕能系统，这意味着随着回复力非线性化程度的增加有助于提高“锁频”区间。同时在风速小于3 m/s或大于4 m/s时，3种捕能系统在摆动角度上差异性较小，这意味着回复力矩非线性化对柱体摆动响应两端风速的影响逐渐减小。

3.2 对横向摆动频率的影响

不同捕能系统随风速变化的横向摆动频谱分析图及变化趋势，如图7所示。其不同风速下的横向摆动频率值，如表1所示。

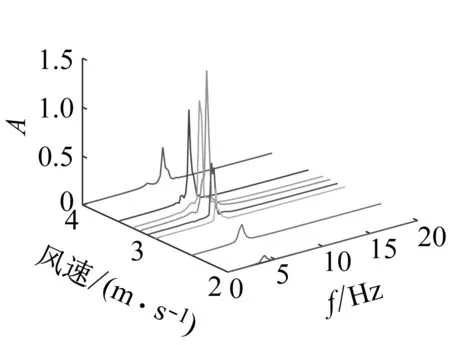
(a) 函数s1

从图7(a)和表1可知，对于具有函数s1的捕能系统，其捕能柱横向摆动频率首先随来流风速的增加而增加，且均表现为 “单峰”振动；随着风速增加旋涡脱落频率增大，捕能柱开始出现“双峰”振动，横向摆动产生次频分量并被“锁定”到固有频率附近，表现为“拍”的不稳定性振动；风速继续增加即达到了频率锁定状态，同时在更高风速下也产生了接近系统固有频率的次频分量。

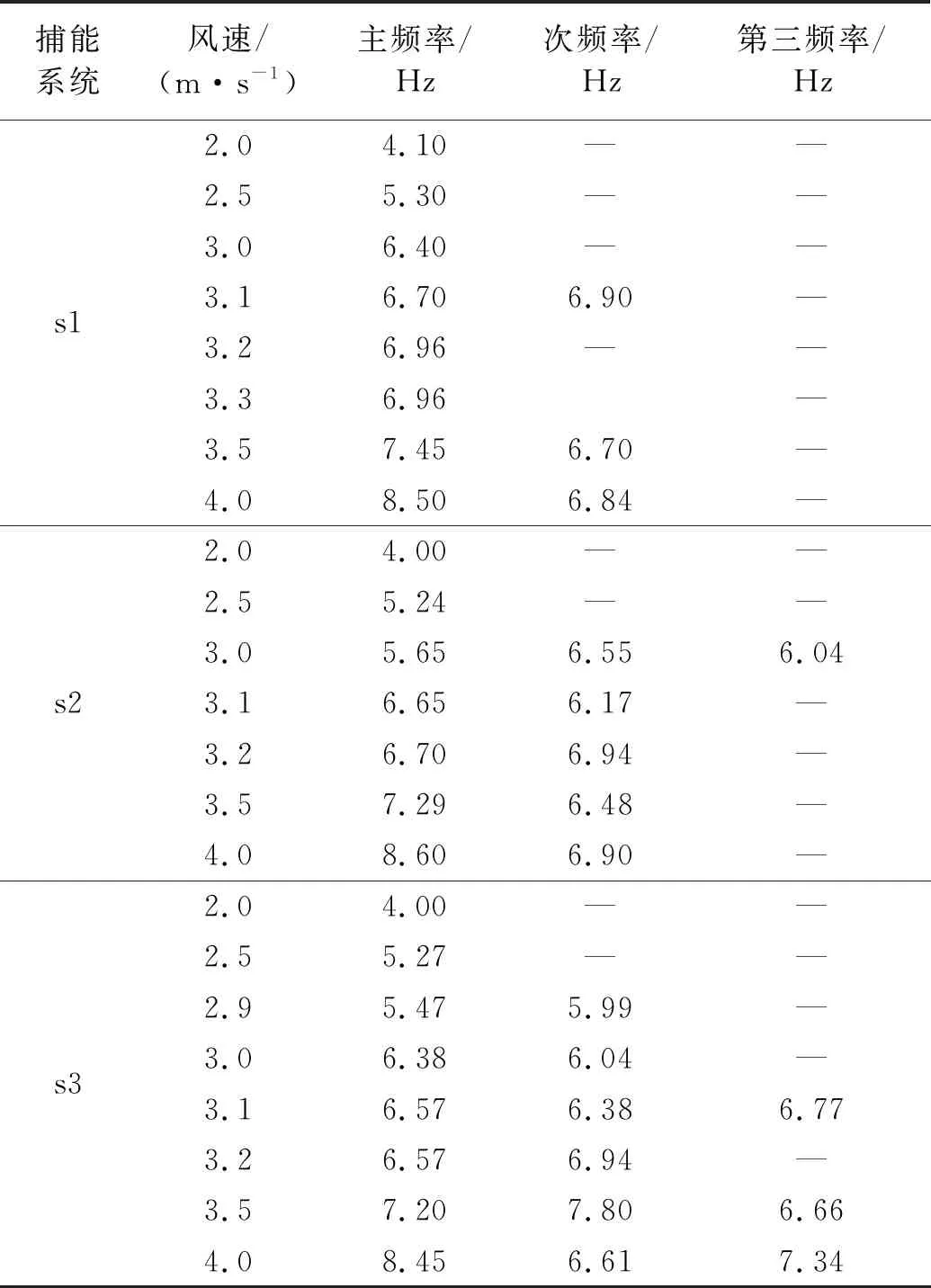
表1 不同捕能系统在不同风速下的横向摆动频率

从图7(b)～图7(c)和表1可知，对于具有非线性函数s2和s3的捕能系统，其捕能柱横向摆动频率出现了较明显的“三峰”现象，即摆动频率产生了3个峰值。这是由于具有非线性函数的捕能系统，其固有频率在摆动过程中发生了变化，所以产生了更多的次频分量，其相应固有频率波动带宽也就增加。当系统的固有频率可变时，结构体与流场将产生更自由的耦合，从而激发更宽泛的振动模态。当非线性捕能系统捕能柱摆动幅度增大时，其系统固有频率能在不同风速下随之增大到与旋涡脱落频率相匹配，这将有助于增大主频锁定的区间。

3.3 对气动力参数的影响

不同捕能系统其升力系数均方根Cl,rms和时均阻力系数Cd统计值随风速的变化曲线，如图8所示。

从图8可知，3种捕能系统在最大摆动角度所对应风速下的气动力参数均了产生波峰。此时旋涡脱落频率与系统固有频率相匹配，结构体与流场强烈耦合，从而增大了柱体的气动力参数。

图8 不同捕能系统气动力参数统计值随风速的变化

对具有非线性回复力的捕能系统，即使其固有频率随摆动角度发生了改变，但也同样能达到频率锁定的强耦合状态，但是其气动升力系数的波峰有所降低。在具有函数s3的捕能系统中，当风速为3.1 m/s时，其柱体的横向摆动表现为“拍”现象，气动升力均方根值相比最大摆动角度下降更为明显。

同时对于远离频率锁定风速区间的“初始分支始端”与“下部分支末端”，回复力矩的非线性化对捕能系统气动力参数的影响逐渐变小。

3.4 对能量捕获效率的影响

不同捕能系统能量捕获效率随风速的变化，如图9所示。

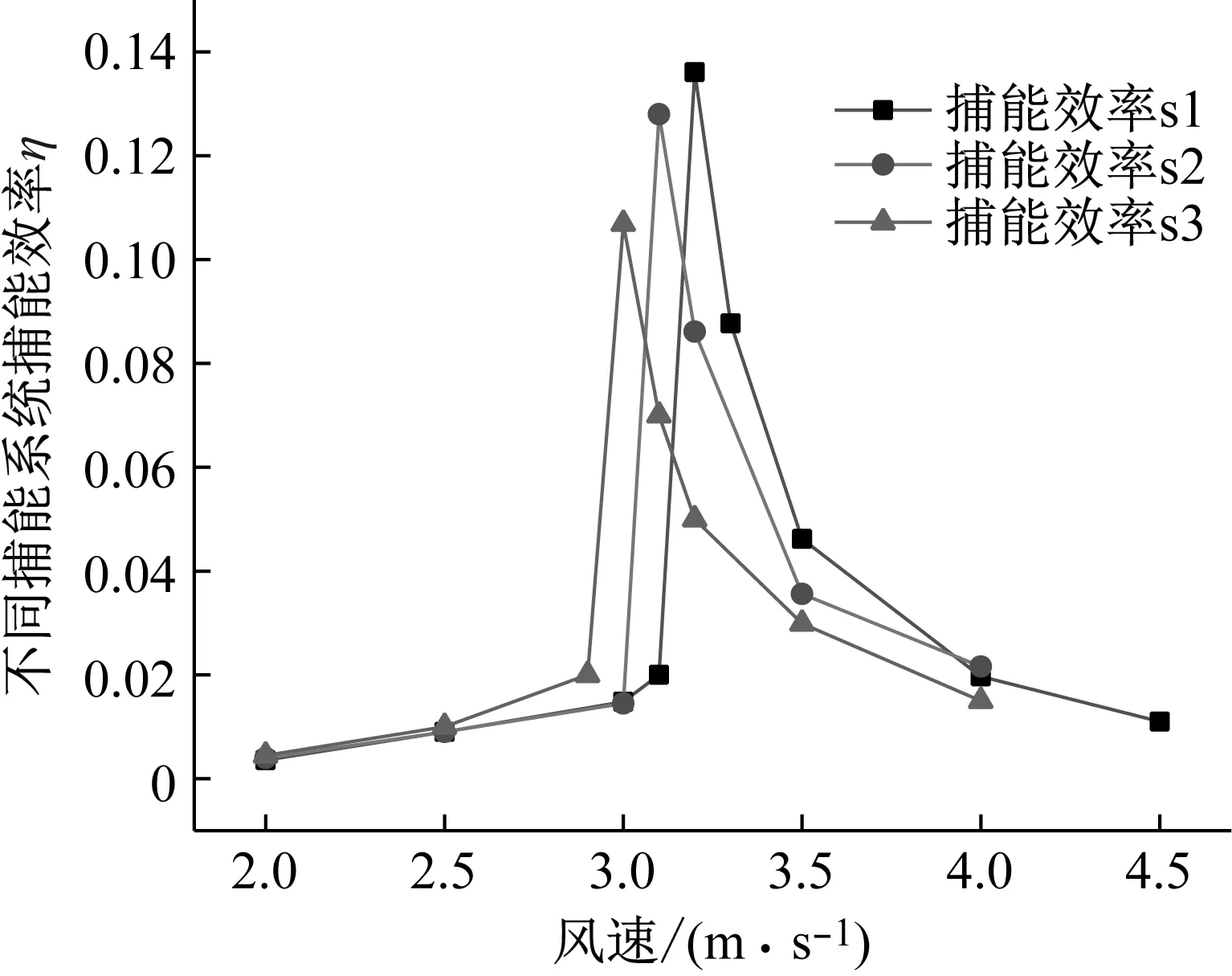
图9 捕能系统能量捕获效率随风速的变化

由图9可知，不同捕能系统能量捕获效率与气动升力系数呈现相应的趋势，峰值能量捕获效率随回复力矩非线性化程度的增加而减小，对应的风速向前推移。在气动升力产生“拍”现象时，能量捕获效率计算值同样表现出较大幅度的减小。

3.5 涡激摆动尾涡结构场

具有函数s1的捕能系统在摆幅峰值风速下一个摆动周期T的三维RANS湍流模型尾涡结构场，如图10所示。

从图10可知，捕能柱向两侧横向摆动时产生了较明显的斜涡脱落，柱体回复到平衡位置时表现为在流向方向交替涡脱落。

(a) t=T+0.25T

相比柱体涡激平行振动，在摆动运动过程中柱体尾涡脱落受到摆动角度的影响，尾涡结构在柱体高度方向发生了不同程度的脱落模态。而涡激平动尾涡脱落模式在柱体高度方向较保持一致，这也可能是导致涡激摆动频率“锁定”区间较窄的一个原因。

4 结 论

本文基于计算流体动力学-刚体动力学耦合的方法，结合SSTk-ω湍流模型和六自由度动网格技术，建立了无叶片风力机捕能柱的三维涡激摆动模型，对无叶片风力机变固有频率系统进行了理论分析，在对所建摆动模型进行验证的基础上，研究了变固有频率系统对捕能柱涡激摆动特性及能量捕获效率的影响，得到以下结论：

(1) 非线性回复力矩函数的斜率控制着捕能系统的固有频率，且回复力矩非线性化程度越大系统固有频率的变化速率越快。

(2) 回复力矩的非线性化程度越大，捕能柱峰值摆幅和能量捕获效率越小，且对应的风速向较小雷诺数方向推移。

(3) 在变固有频率捕能系统中，捕能柱横向涡激摆动次频分量带宽增加，选择恰当的变固有频率系统可增加柱体主频锁定区间和高摆幅区间。

(4) 捕能柱在涡激摆动过程中，随高度方向的变化产生不同程度的斜涡脱落，对涡激摆动频率锁定具有一定的影响。

本文仅对回复力矩的非线性程度进行了探讨，但影响变固有频率的因素还有系统阻尼系数、捕能柱的质量等因素，且针对本文内容的试验测试研究均将是本文作者后续的研究内容。