基于SKF-KF-Bayes的滚动轴承剩余使用寿命预测方法

许艳雷， 邱 明,2， 李军星,2， 刘 璐， 牛凯岑

(1.河南科技大学 机械工程学院,河南 洛阳 471003；2.河南科技大学 高端轴承先进制造与智能装备河南省工程技术研究中心,河南 洛阳 471003)

滚动轴承广泛应用于旋转机械中，是决定机械设备安全可靠运行的关键部件之一，一旦发生失效，设备无法正常工作，甚至会造成巨大的经济损失和人员伤亡。开展滚动轴承剩余使用寿命(remaining useful life，RUL)预测，对于保证机械设备安全可靠运行、提高设备的生产效率具有重要的意义[1-2]。

根据Vichare等[3]的研究，机械设备RUL预测方法可分为两类：基于失效物理模型的RUL预测和基于数据驱动的RUL预测方法。基于失效物理的RUL预测较准确，但随着科技的进步，设备的复杂性也在增加，其退化机理涉及多个学科的知识，建立物理退化模型十分困难；基于数据驱动的RUL预测不需要建立退化机理模型，只需要实时监测产品的退化数据，对于复杂的机械设备较为实用。基于数据驱动的RUL预测包括基于机器学习的RUL预测和基于统计数据驱动的RUL预测[4]。

滚动轴承的退化包括明显的平稳退化和加速退化。在平稳退化阶段，滚动轴承的各项性能指标不会有明显的变化，发生早期故障后，随着工作时间的持续，其性能退化逐渐加剧，直到退化量达到阈值失效。张继冬等[5]基于全层卷积神经网络进行轴承寿命预测，并采用加权平均法对结果进行降噪处理。Elforjani[6]提出了一个线性回归分类器和多层人工神经网络模型，通过联系声发射特征与轴承磨损来估算轴承的RUL。于震梁等[7]提出一种将支持向量机与非线性卡尔曼滤波相结合的RUL预测模型，计算各个时刻RUL的估计值及一定的置信区间。张龙龙[8]发现希尔伯特熵可以较好地分辨轴承的衰退处于哪个阶段，并且利用支持向量机(support vector machine, SVM)建立了预测模型。孙磊等[9]提出一种基于粒子滤波理论的设备RUL预测方法，解决非线性非高斯系统的RUL预测问题。文娟等[10]针对粒子滤波中粒子退化提出一种基于无迹粒子滤波算法的轴承RUL预测方法。Peng等[11]利用伽马过程处理产品的退化过程，采用Bayes方法进行参数估计和退化分析，预测产品的RUL。Pan等[12]采用具有随机效应的逆高斯过程来表征系统的退化过程。然后利用期望最大化算法对模型参数进行估计，并利用Bayes方法对退化模型中的随机参数进行更新，使得估计的RUL能够根据新的退化数据进行实时更新。Lu等[13]将Bayes理论应用于估计设备的RUL分布。Gebraeel等[14]在Lu等的基础上，利用包含布朗运动误差的指数模型拟合滚动轴承的退化轨迹，在Bayes定理的框架下更新模型参数，从而实现了RUL的预测。Wang等[15-16]改进Gebraee提出的模型预测机械设备的RUL。

然而上述RUL预测方法存在各自的不足，机器学习不仅透明度低，还需要大量高质量的训练数据，而这些数据在生产实际中很难获取，与神经网络相比，SVM在处理小样本量问题上更有优势，但目前SVM的参数和核函数的确定有很大的困难；粒子滤波算法同样需要大量的数据才能进行准确预测；逆高斯过程模型与伽马过程模型局限于马尔可夫性质和单调过程；由于滚动轴承退化具有明显的阶段性，如果直接利用指数函数对全寿命试验数据模拟可能会造成较大的偏差，为了提高预测精度，准确区分滚动轴承退化状态是十分必要的。

针对上述①如何准确有效区分滚动轴承退化阶段；②如何在有限数据集中有效结合同类轴承退化数据与待预测轴承实时监测数据。本文提出一种SKF(switching Kalman filters)-KF(Kalman filters)-Bayes相结合的滚动轴承RUL预测方法。SKF不需要设置轴承进入加速退化阶段的阈值根据轴承实时监测振动信号自适应判断轴承退化状态；KF状态方程的确定需要同类滚动轴承全寿命周期的监测数据，Bayes预测时考虑待预测轴承的实时监测数据，有效结合了现有的数据和实时监测数据。

本文主要包括滚动轴承退化状态判断和RUL预测。在退化阶段的判断部分，根据滚动轴承均方根利用SKF判断各个时刻所处的退化阶段，处于平稳阶段的滚动轴承健康状态良好不进行RUL预测。当退化处于加速阶段时，利用包含布朗运动误差的指数模型描述滚动轴承的退化，根据KF单步预测对实时监测数据进行修正继而利用Bayes更新模型参数，确定RUL概率密度函数估计滚动轴承的RUL。SKF不需要设置轴承进入加速退化阶段的阈值根据轴承实时监测信号自适应判断轴承退化状态；随机效应指数模型的使用减少了对高质量数据的依赖；KF单步预测减少实时监测数据的随机性，有效提高了滚动轴承RUL预测的精度；Bayes方法更新模型参数，减少长期预测的不确定性。本文不依赖大量高质量数据和精确的物理模型实现了滚动轴承RUL的准确预测。

1 问题描述

滚动轴承的退化是非平稳的，如图1所示。即滚动轴承各个退化阶段的退化模型是不同的；退化的变点是随机的，即滚动轴承进入加速退化阶段的时刻也是不同的。准确识别滚动轴承进入加速退化阶段的变点，可以提高性能退化建模和RUL预测的精度。

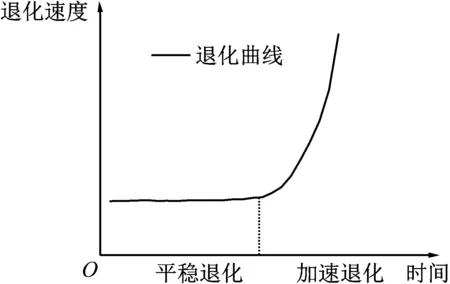
图1 滚动轴承性能退化图

2 滚动轴承性能退化建模

2.1 变点识别方法

本文将滚动轴承的退化分为平稳退化和加速退化两个阶段。由于滚动轴承的差异性，其振动信号不尽相同，当进入加速退化阶段时，均方根的变化也存在差异，SKF可以跟踪滚动轴承退化过程的动态变化，不需要大量的数据训练模型，自适应获得各时刻最可能的退化模型。SKF由多个线性状态空间模型组成，也被称为线性动态模型[17]或交互多模型[18]。

SKF可以被表示为一个动态Bayes网络，如图2所示。每个动态模型St都可以表示为一个基本KF。为确定各个时刻所处的退化阶段，从均方根观测值yt中推断出模型概率St和模型状态xt。

图2 SKF的动态Bayes表示

卡尔曼滤波的预测及更新过程如下。

预测：

(1)

(2)

更新：

(3)

(4)

(5)

(6)

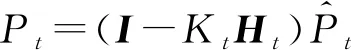
(7)

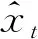
本文将滚动轴承的退化过程分为平稳退化和加速退化，即SKF中包括两个基本KF。模型转移概率Zij为权重，并在加权概率之和上进行归一化。

从测量残差考虑每个滤波器的可能性

(8)

各模型的概率

(9)

状态加权

(10)

协方差加权

(11)

利用状态和协方差加权估计，通过式(1)～式(7)对两个基本的KF进行预测，每个滤波器都产生一个预测状态x和协方差p估计值，然后利用式(8)确定每个滤波器的可能性，得到各模型在当前时刻的概率式(9)，从而确定各个时刻滚动轴承的退化状态。在Lim等的研究中有关于SKF的详细介绍。

2.2 退化建模

从图1可知，当滚动轴承进入加速退化阶段后，其退化趋势接近指数模型，令Y(t)为滚动轴承均方根退化过程。本文假设Y(t)的函数表达式为

(12)

为计算方便，将式(12)取对数变形为

LY(t)=ln[Y(t)-α]=

θ′+β′t+ε(t)

(13)

由已经监测到的滚动轴承均方根LY(1),LY(2),…，LY(ti)，本文中定义

2.3 模型参数估计

2.3.1 初始参数估计

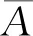
2.3.2 后验参数估计

根据监测数据LY(1),LY(2)，…,LY(tk)，由Bayes定理得θ′和β′的后验分布参数为

μθ′=

(14)

μβ′=

(15)

(16)

(17)

3 滚动轴承RUL预测

3.1 修正实时监测数据

在滚动轴承振动信号测量的过程中不可避免会受到外界的影响，进而导致Bayes更新结果的不准确。利用KF单步预测对滚动轴承实时监测数据进行修正，减少数据的随机性提高寿命预测的精度。

对数据进行对数线性化处理，根据式(1)～式(7)对滚动轴承实时监测数据进行KF单步预测，KF单步预测的状态方程为

L=a+b·t+ε(t)

(18)

式中:a为同类轴承退化数据平稳退化阶段特征值的均值;b为同类轴承退化数据加速退化阶段特征值增量的均值，误差项的计算见2.3.1节。

3.2 RUL分布模型

根据监测数据LY1,LY2,…,LYk，LY(t+tk)为一个正态随机变量，当LY(T+tk)=D时判断滚动轴承失效，T为滚动轴承的RUL，D为失效阈值。T的累积分布函数为

(19)

根据监测数据，LY1,LY2,…,LYk，LY(t+tk)为一个正态随机变量且

(20)

(21)

由式(19)可以得到滚动轴承RUL的概率密度函数

fT|LY1,LY2,…,LYk,T>0(t)=φ[h(t)]h′(t)

(22)

4 工程实例

利用实际试验中获得的滚动轴承全寿命周期振动信号验证本文所提方法的有效性。本文所采用的数据集XJTU-SY[19]是由西安交通大学设计科学与基础构件研究所和浙江长兴昇阳科技股份有限公司提供。试验机结构，如图3所示。试验轴承的型号为LDK UER204；选取载荷p和速度v为加速应力，在3种工况条件下对滚动轴承进行试验，每个工况下试验5个轴承，工况条件如表1所示。试验中水平和垂直方向的PCB 352C33单向加速度传感器同时采集信号，采样频率为25.6 kHz，每1 min采集1.28 s的振动信号[20]。

(a) 试验机整体图 (b) 局部放大图

表1 滚动轴承试验工况表

计算各个试验滚动轴承水平方向振动信号的均方根值，对均方根数据进行滑移平均处理，利用SKF判断工况2轴承各时刻退化状态，如图4所示。图4中:退化状态1表示轴承处于平稳退化;退化状态2表示轴承处于加速退化。由于振动信号的随机性和测量误差的影响，均方根的退化过程不是单调递增的，此时SKF模型识别轴承退化状态的能力减弱，本文中定义滚动轴承连续5个或5个以上时刻的退化状态处于加速退化时，该滚动轴承进入加速退化阶段。对均方根数据进行滑移平均处理后，利用SKF判断工况2条件下各个滚动轴承进入加速退化阶段的时刻，如表2所示。

图4 工况2轴承退化轨迹及各时刻最可能的退化状态

表2 各轴承进入加速退化阶段时刻表

本文利用工况2下2号、3号、4号、5号轴承的均方根退化数据预测工况2下1号轴承的RUL。根据表2获得各轴承进入加速退化阶段的时刻，利用包含布朗运动误差的指数模型式(13)拟合滚动轴承进入加速退化阶段后的均方根退化轨迹，各轴承退化轨迹参数，如表3所示。

表3 轴承退化模型参数表

表4 先验分布参数表

利用KF对实时监测到的振动信号进行单步预测，根据KF单步预测结果和先验分布参数利用式(14)～式(17)得工况2下1号轴承的后验分布参数，继而根据式(20)～式(22)得到工况2下1号轴承RUL的概率密度函数。本文中确定滚动轴承的失效阈值为其他4个轴承失效阈值的平均值，概率密度函数的最高点为RUL的估计值。为了说明本文提出方法的有效性，将本文所提方法与Bayes，相关向量机(relevance vector machine，RVM)预测滚动轴承RUL的方法进行了对比，得到对比结果，如图5所示。

从图5可知，在同样的数据样本下，本文所提预测滚动轴承RUL方法的准确度要远远高于RVM方法，这是因为RVM同SVM一样对参数和核函数有很大的依赖性，但目前比较成熟的核函数及其参数的选择都是根据经验来选取的，带有一定的随意性；本文所提方法有效地减少了实时监测数据的随机性，降低了外界环境对Bayes更新的影响，并且随着预测时间的增加预测精度也在逐渐增大。

(a) 本文方法与RVM对比

5 结 论

针对滚动轴承寿命预测中存在的两个问题：准确区分滚动轴承退化阶段和有效地利用历史退化数据与实时监测数据，本文提出一种基于SKF-KF-Bayes理论的滚动轴承性能退化建模与RUL预测方法。其特点在于① SKF根据轴承实时监测振动信号自适应判断轴承退化状态且不需要设置进入加速退化阶段的阈值；② KF单步预测有效减少了实时振动监测数据的随机性；③ Bayes方法更新模型参数，减少了滚动轴承RUL长期预测的不确定性。通过滚动轴承实例分析，验证本文提出方法不依赖大量高质量数据实现了滚动轴承RUL的准确预测。