长宁页岩气宁纳线大落差管段清管冲击应力与位移分析

彭 阳 安建川 罗 敏 余 进 马学峰 杨 红 别 沁 刘 颖 梁 力

1.中国石油西南油气田公司输气管理处 2.中国石油西南油气田公司

0 引言

长宁—威远国家级页岩气示范区长宁页岩气外输干线宁纳线（宁209井区中心站—纳溪西站）管道外径为813 mm，设计压力为6.3 MPa，设计输气量为1 200×104m3/d，线路总长为110.4 km，为中国石油天然气股份有限公司目前距离最长、管径最大的页岩气外输管道，于2017年12月投运。该管线沿途翻越多处高陡坡地段，其中垂直落差距离超过200 m的大落差管段共有6处。受起伏地形影响，清管器运行速度会不断发生改变，尤其是在大落差管段，会加速冲击管道底部弯头，使得管道所受最大冲击应力可能超过许用值而增加失效风险。因此，为了确保后期清管作业的安全，并为清管方案制订、清管器选型以及清管过程监控等提供依据，有必要对宁纳线大落差管段清管冲击过程进行研究。

现行的标准、规范等侧重于清管作业方案制订、清管器选型、清管安全措施及应急预案实施等[1-3]，对天然气管道的具体清管技术要求较为简略。目前针对大落差天然气管段清管冲击过程的相关研究工作亦开展得不够，主要有：喻军等[4]考虑了管道内压、清管器速度、土壤类型，利用有限元法研究了中缅天然气管道某大落差管段受清管器冲击作用时产生的应力集中及变形问题。李长俊等[5]以云南中缅某大落差管道为研究对象，分析了清管作业时管道内压、积液量、清管器速度和持液率对冲击应力的影响。陈利琼等[6]研究了天然气管道穿越滑坡地段的应力变化规律。贾彦杰等[7]通过分析获得了大落差管道清管器的运行规律。刘啸奔等[8]采用非线性有限元方法，建立了载荷作用下埋地管道弯头的受力模型，研究了弯头曲率半径、弯头夹角、管土摩擦因数与土壤弹性模量等对管道应力变化的影响。曾鸣等[9]以“川气东送”大落差天然气管道为研究对象，分析了橡胶清管球运行速度、内压对清管冲击过程管道应力的影响。陈福林等[10]研究了山区输气管道清管时，高程差引起的重力位能变化对水力计算以及积水对清管速度的影响。刘浠尧[11]针对中缅天然气两段典型大落差管道，研究了不同工况下清管冲击应力与应变。Zhu等[12-13]对清管过程中双向直板清管器与管壁的接触应力参数进行了仿真计算，并比较了线性方法与非线性方法在接触应力计算中的差异性。Zhang等[14]分析了清管器通过环形焊缝时三个阶段的皮碗受力情况。李伟等[15]利用ANSYS/LS-DYNA软件建立了海底悬空管道受坠物撞击的三维非线性有限元模型，研究了接触、摩擦和管—土耦合作用对撞击动态响应过程的影响。邓涛等[16]研究了大落差输气管道水试压后清管的压力脉冲。王文明等[17]采用有限元法研究了清管器对隧道管段的冲击作用，分析了清管器速度、管道内压对管道应力与加速度的影响。丁俊刚等[18]从清管方式、清管器速度和清管安全措施等角度，对比了中国和俄罗斯管道清管技术标准的差异。

综上所述，现阶段对大落差天然气管段清管冲击过程主要影响因素的考虑不够全面，因而不能够充分地了解不同因素对清管器冲击过程的作用规律，并且没有对大落差地段天然气管道敷设时的安全清管极限高度进行研究。为此，以长宁页岩气宁纳线某大落差管段为研究对象，首先分析了不同因素对清管冲击过程的影响；其次基于SPT OLGA软件与ANSYS/LS-DYNA软件，建立了清管仿真模型，计算出清管速度、管道底部弯头所受最大冲击应力及位移；最后，分析得出了大落差管段安全清管条件的计算方法。

1 大落差管道清管过程有限元模型建立与计算

1.1 清管过程仿真几何模型建立

在实际埋地管道清管过程中，管道、清管器与周围土壤三者之间相互耦合，因此，对整个体系进行计算较为复杂。为了便于仿真几何模型建立及提高运算效率，使用了以下假设与简化：

1）大落差管道所处坡面形状为若干折线组成的坡面，管道为直管段不存在弯曲。

2）忽略管道外部防腐层影响。

3）不考虑管内气体对清管器的阻力及升力，清管器只受重力和前后压差。

4）高差主要影响清管器到达底部弯头的速度，故取弯头前端较短长度的管段进行有限元计算。

5）将实际清管器结构进行等质量简化，并将皮碗的密封盘进行等接触面积的集中布置。

以表1中的清管器、管道与土壤的相关参数取值为例，建立起大落差管段有限元模型，如图1所示。

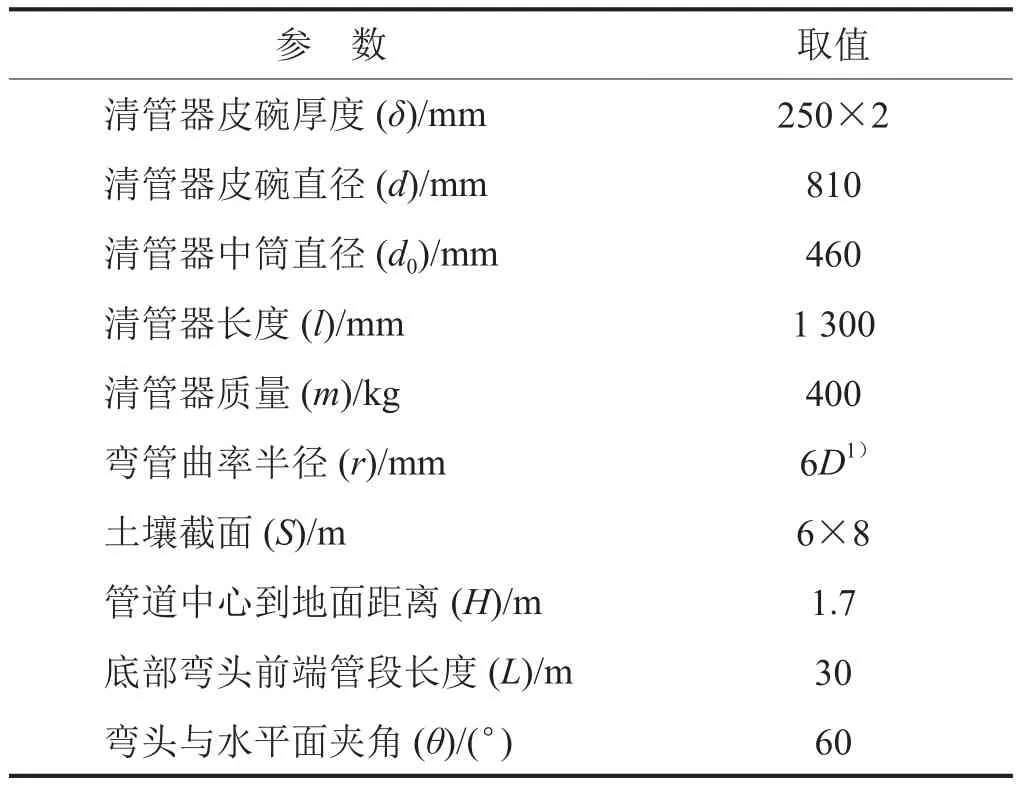
表1 有限元模型建立相关参数取值表

1.2 仿真计算关键参数设置与确定

受清管载荷作用，清管器与管道相互接触。ANSYS软件在计算清管过程时，两个模型的接触力相互传递，同时，也在不断判断两个表面是否发生接触，并不断修正相应约束条件。目标面和接触面的选择依据是将刚度较大的面作为目标面，相应的参数设置见如表2所示。

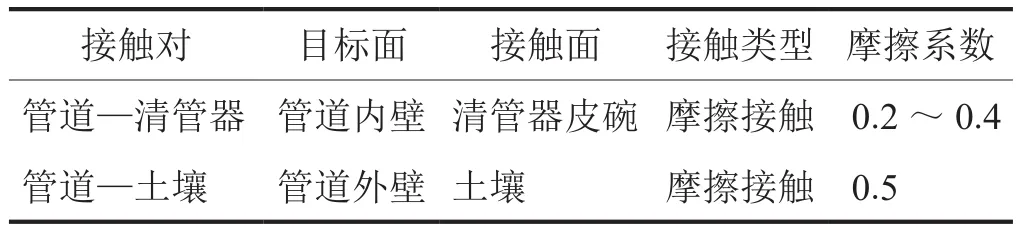
表2 ANSYS软件仿真过程接触条件参数设置表

在进行有限元计算时，需要对所设置的单元赋予材料属性，即选择本构关系。各部分的材料属性选择如下：

1）管道本构关系采用了经典的Ramberg-Osgood模型，ANSYS软件中管道模型参数设置如表3所示。

表3 ANSYS软件中管道模型参数设置表

2）清管器本构模型采用Mooney-Rivlin准则。清管器的中部轴承由结构钢构成，其参数与管材一致。

3）外圈皮碗由可以承受大应变和大变形，但体积改变极微（不可压缩）的聚氨酯构成，因此，选用能够准确描述变形范围为150%以内橡胶材料力学行为的Mooney-Rivlin准则。ANSYS软件中清管器模型材料参数设置如表4所示。

表4 ANSYS软件中清管器模型聚氨酯材料参数设置表

4）土壤本构模型采用的是D-P模型。由于研究的大落差管段所处土壤介质主要为黏土，因此，采用了能够模拟埋地管道周围土壤在清管器冲击作用下力学行为的D-P模型来定义土体介质属性。ANSYS软件中土壤模型参数设置如表5所示。

表5 ANSYS软件中黏土土壤模型参数设置表

在有限元计算中，尽量选择网格质量较高、迭代速度较快的六面体网格，并进行网格无关性验证。以输送压力为4.0 MPa、清管器运行初速度为15 m/s的清管工况为例，通过调整网格尺寸大小对总网格进行控制，选取了 23×104、28×104、33×104、37×104、42×104共5种网格数进行清管冲击过程仿真计算，管道最大应力变化趋势如图2所示。

从图2可以看出，当网格数量超过33×104个时，最大应力保持在203 MPa左右，由此可确定出模型最优网格数为33×104个左右（实际为339 017）。后续对所有清管工况中应力与位移的有限元计算，均采用上述同样的方式进行网格无关性验证，但因计算的工况数量较多，故不再一一赘述。

2 大落差管道清管冲击应力与位移影响因素分析

为了研究清管速度、管道内压、摩擦系数、敷设坡度、清管质量和土壤类型对清管冲击过程的影响规律，在仿真计算时采取了单因素改变的方法，参数设置情况如表6所示。

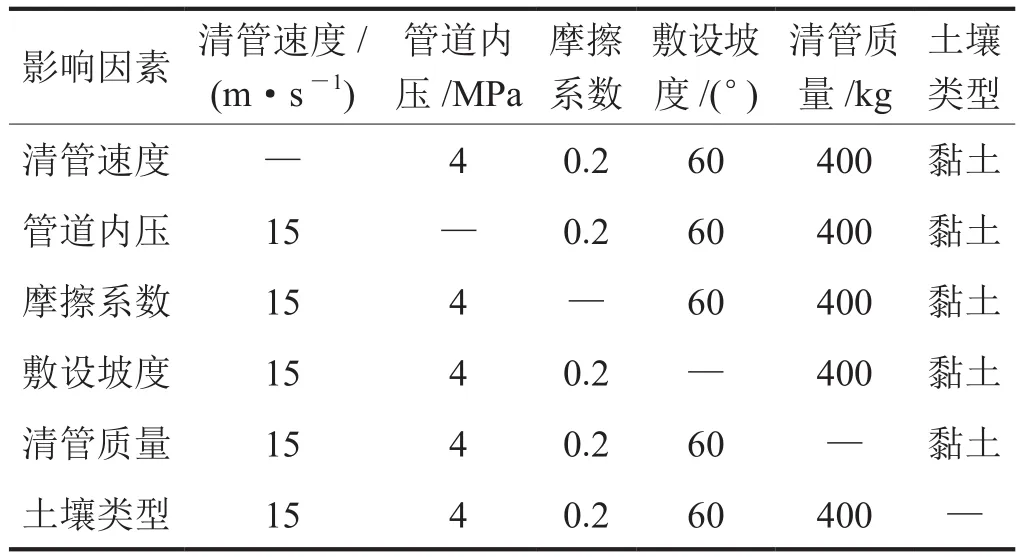
表6 大落差管道清管冲击应力与位移影响因素参数设置表

2.1 清管速度

为了研究清管速度对大落差管段清管冲击过程的影响，设置了较宽的速度范围（3～21 m/s）。不同清管速度条件下，管道所受最大冲击应力与位移变化曲线如图3所示。

从图3可知，随着清管速度增加，最大冲击应力增大，并逐渐接近于许用应力值339.5 MPa；最大位移整体上也呈现上升趋势，尤其是在速度超过12 m/s后，位移值加速上升。其中，应力变化量为88.41 MPa，位移变化量为8.52 mm。这表明清管速度能够显著影响清管冲击过程应力与位移。通过对计算结果进行曲线拟合，得到大落差管道受清管冲击作用时的最大应力、最大位移与清管速度的关系式。其中，最大应力、最大位移的拟合确定系数（R2）分别为0.989 9、0.968 7。可以看出，最大冲击应力是随着清管速度增加而呈现快速上升的趋势，此时，管道的失效风险也迅速增加，但最大位移在清管速度小于12 m/s时的增加幅度很小。综上，清管速度会对冲击过程产生很大影响。

2.2 管道内压

根据宁纳线的实际运行压力和设计压力，将压力研究范围设置为3.0～6.0 MPa。不同内压下管道最大冲击应力与位移变化曲线如图4所示。

由图4可知，随着管道内压增加，最大冲击应力快速上升，且最大位移整体上也呈现快速增加的趋势。其中，当内压为6.0 MPa时，管道所受最大应力为324.1 MPa，接近管道许用应力339.5 MPa。通过数据拟合可得大落差管道受清管冲击作用时的最大应力、最大位移与管道内压的函数关系式。其中，最大应力、最大位移的拟合确定系数（R2）分别为0.995 3、0.986 2。可以看出，拟合曲线呈现平滑上升的趋势，这表明管道内压对大落差管段底部弯头所受的冲击应力、位移影响显著。

2.3 摩擦系数

根据《机械清管器技术条件：Q/SY 1262—2010》中关于清管器皮碗材料的规定[19]，将清管器与管壁间摩擦系数研究范围设置为0.20～0.40。不同摩擦系数下管道最大冲击应力与最大位移变化曲线如图5所示。

由图5可知：①当清管器—管壁摩擦系数由0.20增加至0.30时，最大应力计算值随着摩擦系数的增加而减小，其变化量为31.48 MPa；最大位移计算值随着摩擦系数的增加，呈现先增加后减小的趋势，位移变化范围为14.8～15.9 mm，但变化量很小，仅为1.1 mm，可以忽略。②当清管器—管壁摩擦系数由0.30增加至0.40时，最大应力、最大位移的计算值均随着摩擦系数的增加而增加，其中，应力的变化量为31.38 MPa，位移的变化量为2.29 mm。这表明摩擦系数对清管冲击过程的应力影响较大，而对位移的影响很小。分析最大冲击应力呈现先减小后增加的趋势原因为：由摩擦系数变小（或变大）引起的切向冲击应力减小（或增加）的幅度与由速度增大（或减小）引起的离心力（即施加于管道内表面的正压力）增加（或减小）的幅度不一致。通过数据拟合可得大落差管道受清管冲击作用时的最大应力、最大位移与清管器—管壁的函数关系式。其中，最大应力、最大位移的拟合确定系数（R2）均为1.000 0。从拟合曲线可以看出，摩擦系数对清管冲击过程的应力与位移变化影响存在特殊性。

2.4 敷设坡度

根据天然气管道敷设时的地形地势条件，将坡度研究范围设置为40°～70°。不同坡度下管道最大冲击应力与位移变化曲线如图6所示。

由图6可知，随着管道敷设坡度增加，即坡度越陡，清管器到达大落差管段底部的速度也会随之不断升高，相应的最大冲击应力、最大位移均快速增大。其中，应力的变化量为91.89 MPa，位移的变化量为4.03 mm。这表明敷设坡度能够显著影响清管冲击过程的应力大小。通过拟合数据可得大落差管道受清管器冲击作用时，管道最大应力、最大位移与敷设坡度的函数关系式。其中，最大应力、最大位移的拟合确定系数（R2）均为1.000 0，拟合曲线与计算曲线基本重合。从拟合曲线可以看出，管道敷设坡度对清管冲击应力与最大位移的影响很大。

2.5 清管质量

根据现场清管作业常用清管器类型，包括：直板清管器、测径清管器、磁力清管器、漏磁检测清管器的重量变化范围，将清管质量范围设置为400～1 600 kg。不同清管质量下管道最大冲击应力与最大位移变化曲线如图7所示。

由图7可知，随着清管质量的增加，大落差管道受冲击应力增加或降低幅度并不十分显著，其中，最大应力的变化范围为172.43～178.04 MPa，最大位移的变化范围为15.57～16.80 mm，即应力与位移的改变量均很小。这是因为清管器前后压差始终设置为0.2 MPa保持不变，随着清管质量的增加，清管器运行加速度变小，当到达底部弯头部位时的速度也会减小，从而导致冲击应力减小，但同时质量的增加会引起冲击作用力的增加，由此，最终导致管道所受冲击应力、位移在清管质量改变时未发生较大的且有规律性的变化。为验证这一结论，通过提取仿真模型中清管器到达底部弯头时的速度后得出，清管速度确实为随清管质量的增加而减小。通过拟合数据得出了大落差管道受清管器冲击作用时，管道最大应力、最大位移与清管质量的函数关系式。其中，最大应力、最大位移的拟合确定系数（R2）分别为0.843 2、0.895 4。从拟合结果可以看出，清管冲击过程中的应力与位移变化规律不明显。

2.6 土壤类型

土体性质改变必然导致作用在大落差埋地管道上的载荷发生变化，从而影响清管过程的应力、位移大小。其中，影响土壤弹性模量的黏聚力、内摩擦角是反映土壤性质的重要指标。根据宁纳线《线路工程勘察报告》，其土壤主要为粉质黏土和黏土，弹性模量分别为38.54 MPa和28.59 MPa，清管冲击应力与位移云图如图8、9所示。

从图8、9中可以看出，当管道埋于黏土时，清管过程所受最大冲击应力与最大位移计算值分别为202.81 MPa、15.24 mm，均大于粉质黏土的应力与位移计算值。这表明粉质黏土嵌固能力强于黏土，管道在受到冲击载荷作用时，黏土环境下的管道变形更大，因而应力也更大；而粉质黏土环境下的管道被嵌固得更紧，故其位移变化更小。同时，计算结果也表明弹性模量越大的土壤，嵌固能力越强，清管时管道受到的冲击应力与位移也就越小。

3 大落差天然气管道清管冲击过程实例分析

通过综合考虑不同影响因素，针对宁纳线某大落差管段进行清管过程动力学计算。

3.1 清管过程工艺仿真计算

3.1.1 基础数据输入

为了建立清管工艺计算仿真模型，获取清管过程中清管器运行速度随着位置变化的曲线，需要用到的参数包括：天然气组分、管道沿线高程、管线长度、管径、壁厚、粗糙度、输气量、首站温度、末站压力和环境温度。以宁纳线为例，采用表7中的数据，基于SPT OLGA软件进行清管工艺计算。

表7 宁纳线管道设计及运行参数表

3.1.2 仿真模型建立与校核

选取OLGA Empty File，首末站分别设置为流量节点与压力节点，并结合管段沿线高程数据，加入FA-models中的清管模块（Pigging Model），从而起建立管道清管模型。在网格划分过程中，取每条管段的小节数为4，每节长度取100 m。

通过对宁纳线6次清管作业工况进行仿真计算，并将结果与实际清管采集数据进行对比，以验证所建模型的准确性。首站压力、末站压力及平均速度结果对比如图10所示。

由图10可以看出，在不同清管工况下，首站压力、末站压力及平均速度仿真计算结果与实测之间偏差很小。其中，首站压力计算结果误差范围为0.1%～1.1%；末站压力计算结果与实测值符合得很好；清管器平均速度计算结果误差范围为0.3%～6.4%。因此，采用OLGA软件所建仿真模型计算准确性高，能够用于宁纳线清管过程的模拟。由此，计算出了输气量最大工况（工况3）下清管器通过大落差段的速度为4.3 m/s。

3.2 大落差段清管冲击过程有限元分析

根据现场某大落差管段的实际路由，针对工况3建立有限元分析模型，参数设置如表8所示。清管冲击过程仿真计算网格无关性验证如图11所示，分别 选 取 了 30×104、35×104、45×104、50×104和55×104共5种不同网格数进行最大应力计算，可以看出当网格数量保持超过45×104个时，应力保持在169 MPa左右，由此确定出模型所用的网格总数为45×104个（实际为451 450）。而清管冲击过程应力与位移计算结果如图12、13所示。

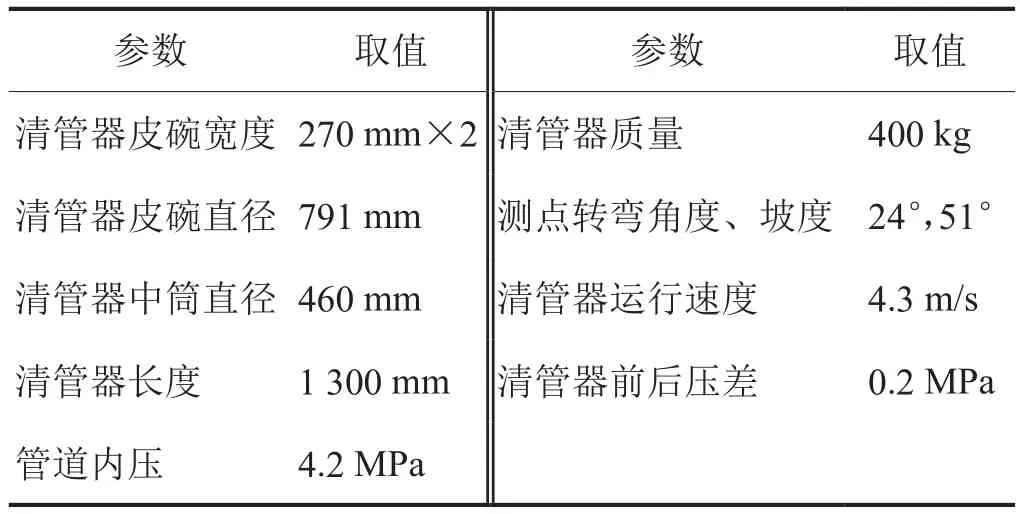
表8 大落差管段清管有限元模型参数设置表

由图12和图13可以看出，管道最大应力为168.72 MPa，最大位移为9.29 mm，应力和位移主要集中在弯头部位。清管过程中清管器的冲击应力并没有超过管道的许用应力值349.2 MPa。因此，上述清管作业工况下清管器的冲击过程是安全的。

3.3 大落差天然气管道安全清管条件研究

3.3.1 已建大落差天然气管道

对于已建大落差天然气管道的某次清管作业而言，可以确定的参数包括：管线敷设路由、管径、壁厚、大落差段高差与坡度、清管器类型、清管器质量以及清管器—管壁间的摩擦系数。管道输气量和运行压力属于变量。这两者均影响清管器运行速度大小，进而影响冲击过程的应力与位移。

为此，首先通过在仿真模型中逐步增加清管器运行速度，以获得管道最大应力刚好大于许用应力时对应的清管器速度，即为极限清管速度；然后，通过清管工艺仿真计算得到对应的输气量大小，从而获得以输量为表征的安全清管工况。以宁纳线为例来进行安全清管工况计算：

1）基础数据输入。管道内压取设计压力6.3 MPa，清管器与管壁摩擦系数取0.2。

2）极限清管速度计算。通过试算不同速度直至管道应力刚好超过管道许用应力349.2 MPa，即为极限清管速度（νmax）。由此可得，当清管器速度为16 m/s时，管道最大应力值为351.1 MPa。

3）最大允许输量换算。通过改变清管工艺仿真模型起点输气量，计算极限清管速度为16 m/s时对应的输气量值。由此可以得出，当输气量增加至设计输气量时，清管器冲击速度为5.5 m/s，低于极限清管速度，即在清管过程中不会出现管道应力超限的情况。

3.3.2 处于设计阶段的大落差天然气管道

对处于设计阶段的起伏地形天然气管线而言，设计输气量和设计压力均已确定。为此，在管线运行最大输气量和压力条件下，先进行极限清管速度计算，然后基于能量守恒方程式推导出由高程差所表征的安全清管条件计算式。计算公式为：

式中m表示清管器质量，kg；H表示管段的垂直落差，m；F推力表示内压产生的推力，N；F摩擦表示清管器与管内壁之间的摩擦阻力，N；L表示斜坡内管道长度，m；νmax表示极限清管速度，m/s；ν0表示清管器到达坡顶的速度，m/s；Δp表示清管器前后压差，MPa；A1表示管道内截面积，m2；f表示摩擦系数；θ表示管道与水平面的夹角，（°）；pr表示清管器与管壁间的接触应力，MPa；A2表示清管器与管壁的接触面积，m2。

同样，以宁纳线为例说明如何确定出以高程差为表征的安全清管条件：

1）清管工艺计算。在设计输量条件下，清管器运行至坡顶时的速度为5.3 m/s。而在计算极限清管速度时，管道内压取设计压力6.3 MPa，清管器与管壁摩擦系数（f）取0.2。

2）极限清管速度确定。由3.3.1可知，清管器极限速度为16 m/s。

3）利用式（1）计算得出安全清管高差为852 m。因此，当管道实际敷设的高度小于852 m时，清管过程是安全的；反之，管道则会产生失效的风险。

4 结论

1）随着清管器运行速度、管道内压和敷设坡度的增加，清管器对大落差管段底部的冲击应力值增大趋势明显，但位移值涨幅不大。

2）当清管器—管壁的摩擦系数由0.2增加至0.4时，清管冲击过程的应力与位移变化存在特殊性，且摩擦系数对清管冲击过程的应力影响较大，而对位移的影响很小。最大冲击应力呈现先减小后增加的趋势原因为：由摩擦系数变小（或变大）引起的切向冲击应力减小（或增加）的幅度与由速度增大（或减小）引起的离心力变化的幅度不一致。

3）对于不同类型的土壤，弹性模量越大，对管道的嵌固能力越强，因而管道所受的冲击应力与位移也就越小。

4）通过对宁纳线某大落差管段进行清管动力学计算，验证了基于OLGA软件的清管工艺仿真模型准确性，得出了在目前清管作业工况下，清管器冲击过程是安全的。

5）通过对已建大落差天然气管段清管极限速度计算，得到了以输量为表征的安全清管条件；对于处于设计阶段的大落差天然气管道而言，确定出了以高程差为表征的安全清管条件。