基于卷积自编码网络的瓷砖表面缺陷检测

李泽辉，陈新度，练洋奇

（1.广东工业大学，广东省计算机集成制造重点实验室，广州510006；2.广东工业大学，省部共建精密电子制造技术与装备国家重点实验室，广州510006）

0 引言

我国是瓷砖生产大国，国内的墙地砖生产企业在原料加工方面已实现了机械化和自动化，但在分色分级方面仍停留在人工检测的水平，在瓷砖的生产流程中，从原料、配方、球磨、制粉、成形、烧制到磨边倒角等，各个环节均会产生不同的缺陷，其中主要包括孔洞、划痕、杂斑等类型表面缺陷。近年来许多学者提出了基于传统机器视觉的瓷砖表面缺陷检测方法，其中Sameer Ahamad等[1]对瓷砖进行亮度增强和中值滤波的预处理后，分割瓷砖图像并进行特征提取，然后利用图像直方图测量瓷砖缺陷，实现了对陶瓷缺陷分级。S.H.Hanzaei等[2]提出用旋转不变测量局部方差算子特征提取缺陷特征，经过形态学增强后利用支持向量机进行缺陷分类，取得了较好的效果。但这类方法往往采用常规图像处理算法或人工设计特征加分类器方式，在实际应用中存在算法参数调试困难，鲁棒性不强，容易被复杂工业环境影响等缺点。近年来，开始有学者将卷积神经网络用于工业缺陷检测，许志鹏等[3]提出了基于轻量YOLOv3的拉链缺陷检测系统，模型达到80%的mAP。一些研究者利用分割网络如FCN、U-Net进行缺陷检测，可以获得缺陷的准确位置及类型。但这类网络都需要一定数量的标注样本进行训练，而人工标注样本非常耗时。针对这一问题，有学者提出无监督学习网络，其中Goodfel⁃low提出的生成式对抗网络（generative adversarial net⁃works，GAN）被广泛运用于数据生成、图像恢复等领域，Zhao等[4]提出一种基于GAN的织物表面缺陷检测方法，该法通过修复缺陷区域后和原图对比来检测缺陷，但只适用于均匀纹理的表面。Masci[5]提出另一种无监督学习网络卷积自编码器（convolutional auto⁃encoder，CAE），Ke提出一种基于CAE的异常值检测网络来检测缺陷区域，还有许多基于CAE的表面缺陷检测研究，但多是针对规则纹理样本[6]。

基于以上研究，本文提出一种基于轻量卷积自编码网络的瓷砖表面缺陷检测方法LR-CAE，该法通过对无标注的正常瓷砖样本进行弱缺陷图像重构训练，使网络获得对正常纹理而非缺陷特征的重构能力。当缺陷样本输入时，网络会因为对缺陷区域不敏感而导致重构图像的原缺陷区域相对原图表现出差异，最后通过残差处理加阈值化操作就可以获得潜在的缺陷区域。

1 数据集制作

瓷砖幅面为600 mm×600 mm，采集得到共80张完整瓷砖图像。采集得到的图像受到成像系统等环境因素影响，经过分析存在较多噪点，故利用中值滤波先进行一次滤波操作。本文的目的是通过易于获得的无标注正常样本来训练网络，首先利用仿射变换校正瓷砖位姿以方便后续的区域划分操作。然后提取仅包含瓷砖的区域图像，为了适应较大图像输入，将原图划分若干小区域，再经过旋转、添加随机高斯噪声共得到2328张无缺陷瓷砖图像，60张缺陷图像。

图1瓷砖分块图像

2 基于卷积自编码的表面缺陷检测方法

2.1 卷积自编码器

2.1.1 卷积自编码器原理

自编码器最初由Rumelhart等提出，并将其应用于复杂高维数据处理。自编码器结构如图2所示，但自编码器只采取了全连接网络，原理是依靠sigmod、tanh和relu函数对数据进行非线性映射来获取特征编码[7]，但这种结构忽略了图像的局部空间结构信息，同时全连接层的使用使得模型整体参数量过大难以优化。

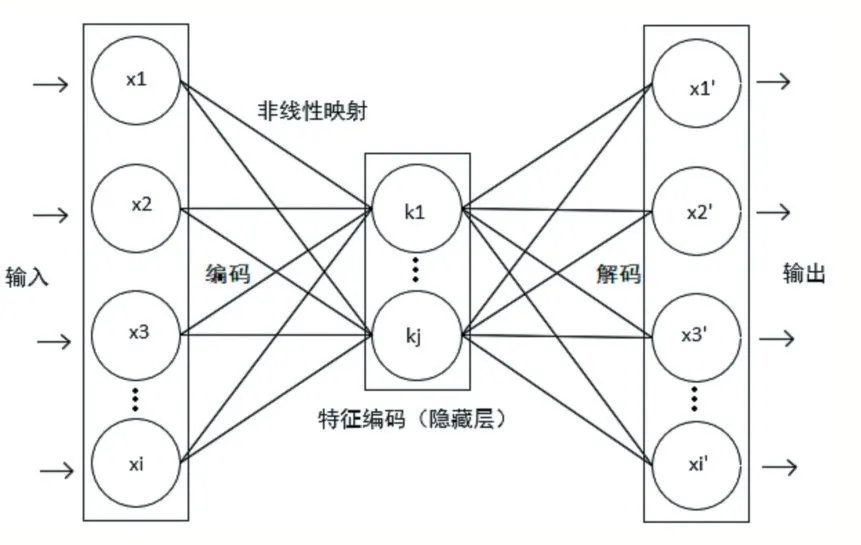
图2自编码器结构

卷积神经网络（Convolutional Neural Networks，CNN）的提出使得特征提取变得更加合理并且大大减少了参数量，得益于CNN的思想，CAE在特征编码前加入了卷积层进行特征提取，并在特征解码加入反卷积层进行重构操作。

CAE的网络结构如图3所示，相比传统的AE，CAE的优点是利用了卷积操作来进行特征提取以及特征降维，同时网络的权值由所有神经元共享，这使得网络能够学习到数据的空间表示，保持了图像空间的局部性，并且使得模型易于训练，重构效果更好。

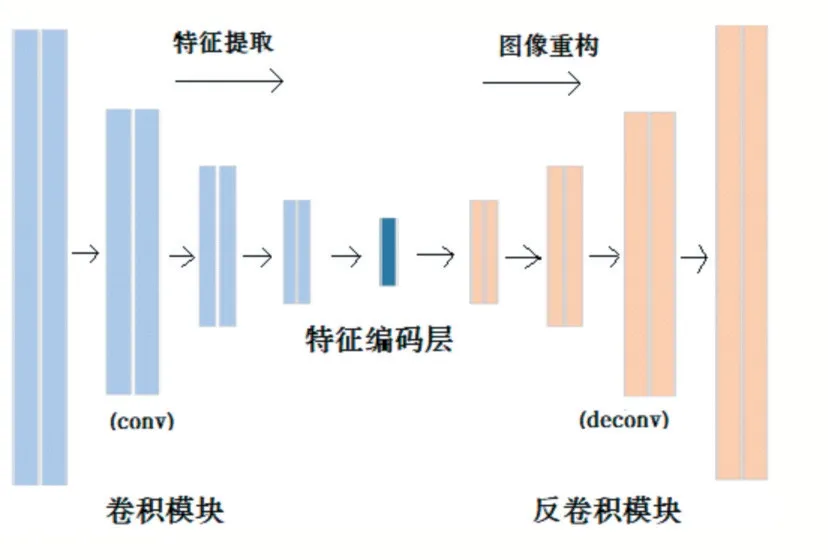
图3卷积自编码器结构

CAE的编码过程如下，对于输入的原图Isrc的每个通道图X，利用k个权值为Wi，偏置为bi，i=1,…,k的卷积核对通道图做卷积，则可以得到k个特征编码图，编码原理如式（1）所示。

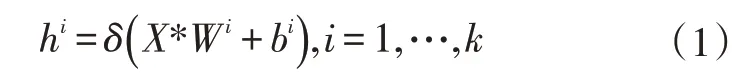
图像重构也就是解码的过程，则是由反卷积操作完成，通过反卷积操作可以实现从编码特征到重构图像的转换。解码原理如式（2）所示，其中H表示上一层操作后得到的特征映射图，W͂i是反卷积操作时卷积核的权值，c为偏置，Y是解码后得到的对应通道图。

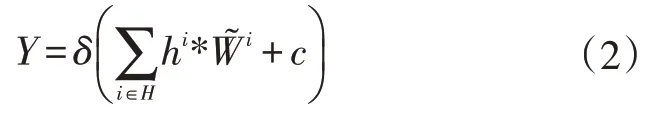
为了提高模型提取特征的能力，Vicent等[8]提出了CDAE（卷积去噪自编码器），该网络通过在训练时人为添加随机噪声来提高模型对特征的提取能力。Mei等提出了多尺度重构网络MS-CADE[9]，通过融合多尺度特征来获得质量更好的重构图像。

2.1.2损失函数

在卷积自编码网络中，多采用均方误差（Mean-Square Error，MSE）作为损失函数。MSE也称为L2 loss，一般用来评估两幅图像之间的像素级差异，在图像重构网络中被用作衡量重构图像与输入图像之间的像素级差异程度。该函数侧重于图像的全局差异，定义如下：

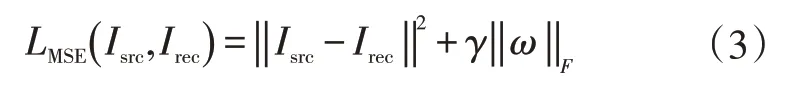
由解码后得到的各通道图Y合并得到，ω表示重构网络中的权重矩阵集，γ表示正则化项的惩罚因子，0<γ<1。从公式可以看出，该损失函数没有考虑局部纹理特征，故以MSE为损失函数的修复模型在规则纹理样本如纺织品等上表现较好，而在样本为不规则纹理的情况下会导致模型难以训练[10]。

2.2 重构网络框架搭建

2.2.1 基本框架选择与改进

基于缺陷样本较少，正样本较多的情况，采取仅需要正样本进行训练的卷积自编码网络作为基本架构，在保持网络形状的前提下针对检测对象对网络进行了修改。本文的网络架构如图4所示，网络呈现对称结构，左侧是由卷积与池化层组成的特征提取网络模块，中间由全连接编码层组成，右侧由上采样与卷积层组成的反卷积重构模块，结构上与特征提取模块基本对称。

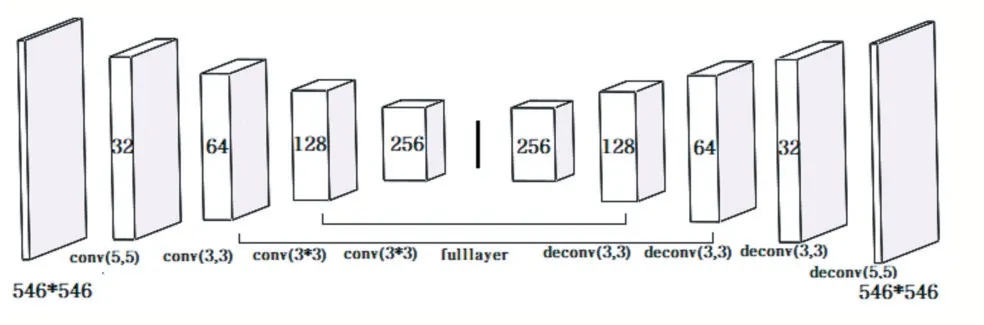
图4 设计的自编码网络模型

经过实验尝试，发现直接从特征编码层经过反卷积操作难以恢复高分辨率图像信息，故参考了U-Net[11]的结构，将对应的卷积层特征图与反卷积层特征图融合，通过将高层的语义信息与底层的纹理信息进行融合，提高了传统CAE结构对高分辨率内容的重构能力。每个网络层均采用ReLU激活函数，并且采用了BN（Batch Normalization）与Dropout加快模型收敛以及防止过拟合。

2.2.2 训练策略与损失函数选择

目前卷积自编码网络中较多使用MS E损失进行训练，根据式（3）MSE损失的定义，其不足以表达人眼对图像的直观感受，人眼衡量两幅图像的距离时，更偏重于考虑两图的结构相似性而不是逐像素计算两图差异。对于不规则纹理样本，采取MSE损失会出现模型训练开始阶段难以收敛的问题。针对这一问题，参考Wang[12]提出的图像结构相似性准则（struc⁃tural-similarity-based image quality，SSIM），SSIM综合考虑了图像在亮度、对比度，以及结构3个方面的相似性，定义如下：

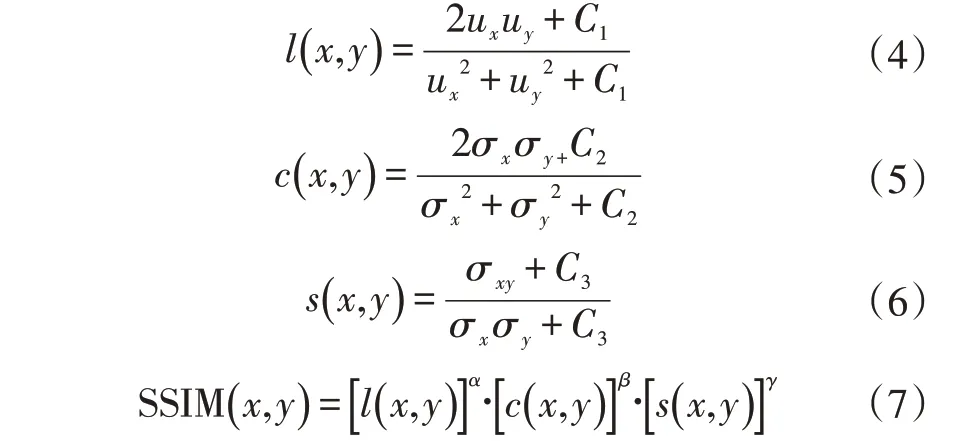
其中l、c、s分别衡量两幅图像x、y在亮度、对比度及结构上的相似程度，μ、σ分别表示图像均值和标准差。SSIM则由式（7）给出，其中α>0，β>0，γ>0，C1，C2，C3是非零常数，通常取α=β=γ=1，C3=C2/2。根据SSIM定义，SSIM损失可以定义为：

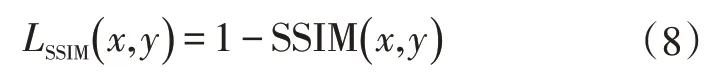
本文提出先使用SSIM损失来进行初始训练，后使用MSE损失训练网络的训练方法。前期使用SSIM损失进行训练可以让网络获得重建底层的纹理结构的能力，然后采取MSE损失函数进行进一步训练以获得更丰富的图像信息重构能力，为了避免模型过拟合出缺陷区域，在后面的训练中以SSIM作为迭代终止条件，但不参与反向传播，目的是防止模型过拟合获得重建缺陷区域的能力。

2.3 缺陷定位

对于训练好的网络，输入待检测的缺陷图像可以得到一副缺陷弱化的重构图像，两幅图像作残差处理可以得到潜在缺陷位置的缺陷图。残差图存在一定的随机噪点，采取3×3的中值滤波作去噪处理，最后通过自适应阈值方法即可得到缺陷的二值图像。从5图中可以看出，网络重建时只能够重构出非缺陷区域，而缺陷区域由于缺乏重构信息而呈现出信息丢失的情况，原图与重构图作残差处理后即可得到缺陷图像。

图5实验结果

3 实验结果与分析

本次实验配置环境为64位Windows 10系统，16G内存，采用NVIDIA GTX 1060 GPU进行训练，采用的深度学习框架为PyTorch。训练的无缺陷瓷砖数据集600张，验证集60张，包含孔洞、溶洞、划痕等缺陷。采取上文所提出的训练策略，经过实验尝试，在SSIM loss达到0.85时终止迭代，继续训练会导致模型最后的验证精度下降。

3.1 方法评价指标

实验的评价指标为最后能否检出正确缺陷区域，采用精确率（Precision）与召回率（Recall）来衡量。两者定义如下：

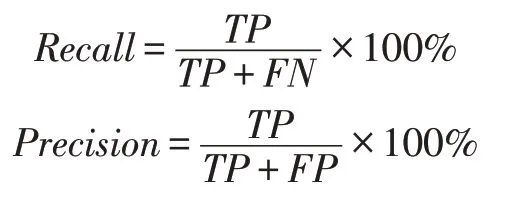
其中TP表示正确被检出缺陷且区域正确的缺陷样本，F N表示没被检出缺陷的缺陷样本，FP表示被错误检出缺陷的无缺陷样本。F1-Measure是同时考虑了精确度与召回率的综合评估指标[13]。

3.2 对比分析

通过实验，对比了近来较为优秀的重构网络CA⁃DE，结果表明网络过深以及单独使用MSE损失训练会让网络重建包括缺陷在内的原图区域，此时经过残差处理的图像无法凸显缺陷区域，也无法通过直接阈值来获得缺陷位置。图6显示了本文网络与CADE网络的残差图结果对比。

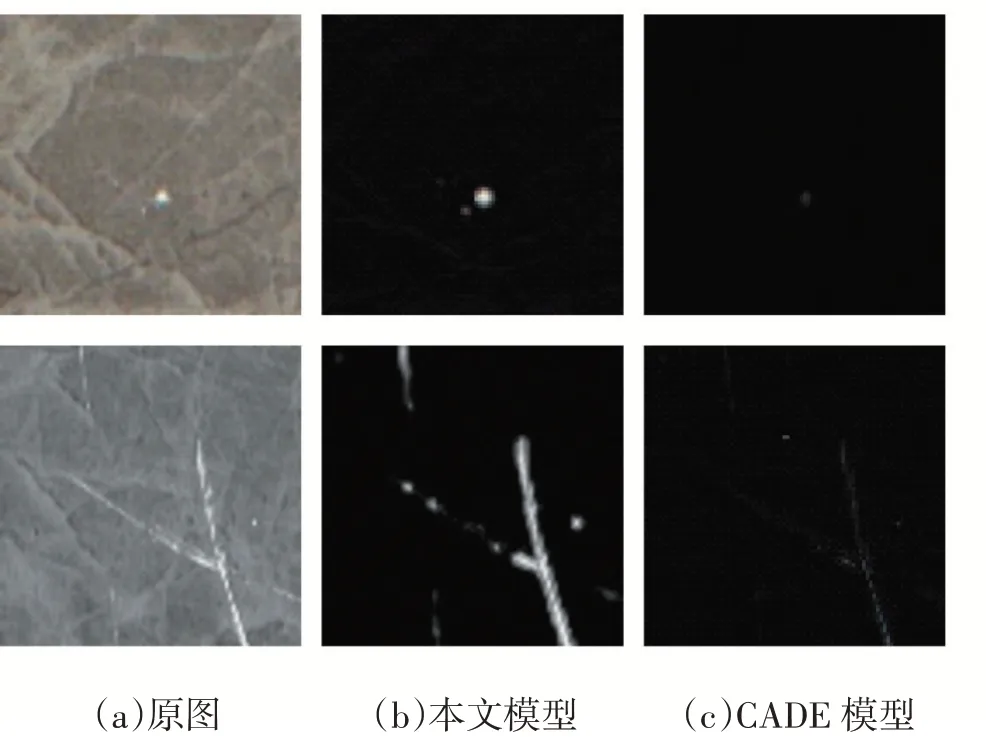
图6残差结果对比

3.3 实验结果

为了验证本文提出方法的有效性，从瓷砖的切片图像中选取60张带有缺陷的图像，其中缺陷包含深划痕、浅划痕，以及孔洞类型。待测图输入到训练好的LR-CAE网络得到弱缺陷重构图，残差操作后结合中值滤波[14]与自适应阈值方法[15]得到最后检测结果。表1展示了实验最终结果。

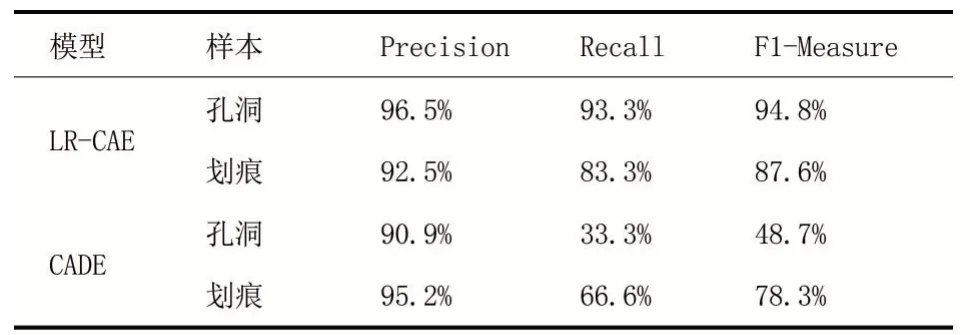
表1实验结果

从表1中可以看到，虽然两个模型的检测精确度都在90%以上，但CADE模型的召回率相对较低，这是因为CADE模型虽然具有较好复现特征能力，但也同时提高了对缺陷区域的复现能力，导致最后重构出来的图像缺陷区域弱化不明显，残差操作无法获得明显的缺陷图像，例如针孔这类本身尺寸就比较小的缺陷就容易出现漏检。从表1中也能看出，本文的方法则对两种类型的缺陷都具有较好的检测效果，两类缺陷的F1-Measure评价指标分别达到94.8%和87.6%，相比CADE有较大提升。

4 结语

本文针对部分类型瓷砖的纹理不规则性、背景纹理的干扰性，提出一种基于轻量卷积自编码的瓷砖表面缺陷检测方法，在训练模型时仅需要输入无标注的正常样本，避免了对人工标注样本的依赖。并且轻量化的结构使得网络参数较少，易于训练，检测阶段通过将待测图输入该网络可得到弱缺陷重构图，再通过残差和自适应阈值处理即可实现缺陷定位。此外采取了先用SSIM损失训练得到一个较优的网络初始权重后再使用MSE损失训练的策略，解决了单独采用MSE损失函数在样本纹理不规则情况下网络无法收敛的问题。最后实验表明，本文提出的方法在瓷砖孔洞和划痕的检测上取得91.2%的平均F1-Measure，具有较强的鲁棒性，同时网络训练时不需要缺陷数据样本，对其他类型的瓷砖或者工业产品的表面缺陷检测具有参考价值。