基于K-means聚类算法的物流配送方案设计

罗平娟，张胜礼

（兴义民族师范学院，信息技术学院，兴义562400）

0 引言

在数据挖掘的众多算法中，聚类算法是机器学习的入门基础算法，同时也是作为数据挖掘算法中其他分析算法的一个预处理步骤。K-means是迭代动态聚类算法中的一种，也被称为K-平均或者K-均值算法，是一种无监督学习的方法，是许多领域中常用的统计数据分析技术。在物流迅速发展的现代社会，设计一个合理、优化、高效率的配送方案可以大幅度提高工作效率，基于K-means算法设计的思想，使用Python语言强大的matplotlib、numpy库等作为基础编程语言[1]，通过迭代过程把配送点的数据集划分为不同的区域类别，以就近原则分配各区域的配送车辆和人员，能有效节约人力物力资源。

1 K-means算法的基本思想

K-means算法是一种使用较为广泛的聚类算法，其中K表示类簇个数，means表示类簇内数据对象的均值，它是将各个聚类子集内的所有数据样本的均值作为该聚类的代表点，通过迭代过程把数据划分为不同的类别，使得评价聚类性能的准则函数达到最优[2]。

1.1 K-means算法的步骤[3]

（1）首先，我们随机选取K个对象作为初始的聚类中心，要想知道使用的类的数量，需要快速地查看一下数据，并尝试识别各种不同的分组。

（2）然后计算每个对象与各个聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。距离的度量手段有很多种，常用的欧氏距离、曼哈顿距离等。例如假设数据集X包含n个数据点，需要划分到K个类。类中心为用集合U表示。聚类后所有数据点到各自聚类中心的差的平方和为聚类平方和用J表示，J值为：

聚类目标是使得J值最小化。

（3）聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了，每个聚类的聚类中心会根据聚类中现有的对象被重新计算。对一组迭代重复这些步骤，然后选择看起来对它提供了最好结果的来运行。

1.2 K-means算法的流程[4]

输入是样本集D={x1,x2,…,xm}，聚类的簇树K，最大迭代次数N；输出是簇划分C={C1,C2,…,Ck}

（1）从数据集D中随机选择K个样本作为初始的K个质心向量：{u1,u2,…,um}

（2）对于n=1,2,…N

1.3 3种K-means的优化算法简介[5]

（1）K-means初始化优化K-means++。在K-means算法中K个初始化的质心的位置完全是随机选择的，有可能导致算法收敛很慢，K-means++算法就是对K-means随机初始化质心的方法的优化。

（2）K-means距离计算优化Elkan K-means。此算法就是从距离简化计算入手，减少一些不必要的距离的计算。

（3）K-means大样本优化Mini Batch K-means。在K-means算法中要计算所有的样本点到所有的质心的距离，如果遇到样本量非常大，例如达到10万、100万以上是非常耗时的，Mini Batch就是用样本集中的一部分的样本来做传统的K-means，这样可以避免样本量太大时的计算难题，算法收敛速度大大加快。

这3种优化算法在后期数据挖掘的算法中再进行应用，本文中选取K-means的基本算法来介绍物流配送方案的设计。

2 基于K-means算法物流配送方案

2.1 问题的提出和分析

贵州省兴义市某物流公司要给兴义市黄草街道的100个客户配送货物。在“双十一”期间由于公司车辆有限，现分别设计两套备用方案进行配送，一是假设公司只有5辆货车进行配送；二是假设公司只有2辆货车进行配送，客户的地理坐标在testSet.txt文件中，如何配送效率最高？

问题分析：可以使用K-means算法，将文件内的地址数据聚成5类或者2类，从聚类结果把每类的客户相近地址进行划分后，可以分配给同一辆货车，以保证在最短距离类进行合理的配送。

2.2 用Python语言实现K-means算法[6]

首先，导入Python语言中的numpy和matplotlib库，进行数据的统计分析和图形的分析，再进行这100个配送点之间精准距离的计算，其代码如下：

其次，实现K-means算法，因为种子的数量不确定拟定为K（K=5或者2），这时取K个数据点作为聚类的中心，确定每个簇的数据点和中心点。在初步确定簇的数据点和中心点后，把每个数据点依据最短距离分配到最近的簇，用while循环如此反复进行中心点和数据点的确定直至达到最佳效果，其关键代码如下：

最后，使用函数 def show（dataSet, k, classCenter，clusterPoints）（详细代码部分略）进行聚类结果的显示，这里将在city.png图片中根据每个对象的坐标绘制点，把不同划分区域的位置点用不同颜色进行代表，并在相同的簇类找到其中心点，以便配送时进行参考。程序结束部分设置K的值，对源代码部分进行调用和图片的显示，其代码如下：

这样，在通过计算分析后，客户的地理坐标位置就可以清晰地在地图上进行显示，而且根据货车数量的不同，将显示不同的配送方案。如图1所示，是5辆货车的分配图，图中每个区域根据聚类的位置在循环多次后确定各个中心点，再根据中心点的邻近数据确定区域的族，中心位置用红色三角形标注，围绕中心位置的各数据点用不同颜色的圆形、矩形、三角形等进行区分。这样，从图中可以很方便快捷合理对车辆进行分配，节省了人力物力资源。

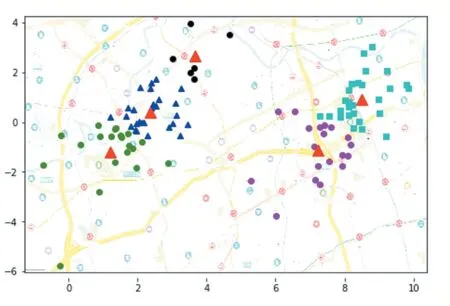
图1 5辆货车配送

但是，在实际分配中，我们还需要为用户考虑更周全的方案，也就是当5辆物流车遇到特殊情况，不能同时出发完成任务时的备选方案。例如，做出一个比较不理想的假设，当只能有2辆货车工作时，这时如图2所示是仅仅只有2辆货车的分配图。这时，初始代码没有发生较大的改变，在设置的参数中把种子的数量K的值由5变成2，重新运行程序后即可得到新的分配方案。同理，当用户调整不同数量的货车，我们都可以进行较小改动即可完成用户的需求。

图2 2辆货车配送

从上例方案的设计中可以看出，配送方案的代码确定后，当K=5和K=2的取值不同时可以生成不同的配送图，这样通过简单的计算即可为客户选择最优的方案既节省了劳力物力又提升了工作效率，很大程度上减轻了“双十一”期间的配送压力。所以，Kmeans算法结合Python语言中的numpy和matplotlib库进行数据的统计分析和图形的分析，是一种较为实用、省时省力的优化设计，能利用Python强大的第三方库面向对象进行有针对性的算法设计，这也是我们在进行机器学习道路上比较有效的方法和途径。

3 结语

通过实践的应用可以看出K-means算法是机器学习中的一种简单实用的算法，利于初学者进行实战分析应用，其优点有：

（1）计算复杂度低，为O（Nmq），其中N是数据总量，m是类别（即k），q是迭代次数。

（2）原理简单，实现容易，收敛速度快，算法的可解释度比较强。

（3）聚类效果较好，可以发现新知识、新规律。

（4）聚类也是了解未知世界的一种重要手段，可以单独实现，也可以作为其他学习任务的前驱过程。

但是K-means算法也存在一些弊端和不足：①需要提前确定K值（类别），分类的结果依赖于分类中心的初始化，每个样本只能有一个类别（属于“硬聚类”），对于带状（环绕）等非凸形状没有团状的数据点集区分度好；②初始聚类中心的选择如果出现偏差对聚类结果有较大影响，使用迭代方法有时会得到局部最优的结果；③K-means算法的时间开销比较大、功能具有局限性等问题[7]。所以在初始聚类中心的选择时会考虑使用K-means++或者Elkan K-means算法，在进行大样本分析时会考虑使用Mini Batch K-means。

通过此方案的设计与实现，让我们感受到数据挖掘算法改变传统思路的优越性，但是仅一种算法的设计应用还存在诸多的问题和不足，需要我们再深入学习把更多的数据挖掘算法进行多方位多角度的结合，才能更好地进行数据的分析汇总，才能适应如今飞速进步发展的大数据时代。