提炼关键问题 发展核心素养

魏远金

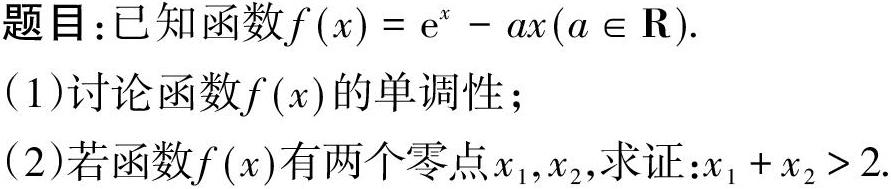
[摘 要]在教学中如何将新课程理念与教学实践进行深度融合，如何从知识传授、机械训练、死记硬背向数学学科核心素养、数学能力的培养转变是我们一线教师思考的关键问题.

[关键词]核心素养;问题;关键;提炼

[中图分类号]    G633.6        [文獻标识码]    A        [文章编号]    1674-6058（2021）29-0005-03

在平时教学中，学生总喜欢问教师：这道题有没有固定的解法能够快速求解？教师通过知识点归纳、典型例题讲解、相似题目训练使学生对一些固定的类型题形成套路的解法.但是，数学题目千变万化，往往改动其中一个条件就能使题目的难度大幅度增加，甚至对题目的思考、解决方式与原题相比发生根本性变化.很多时候，学生感觉题目非常熟悉，但就是不能顺利解决或没有头绪，原来的解法“套路”已经不灵了.

出现这种问题的原因是学生在学习中注重“刷题”，教师对关键问题的挖掘、提炼不够重视，对学生学科核心素养、关键能力的培养较少.教育部《关于全面深化课程改革落实立德树人根本任务的意见》明确指出：应研究提出各学段学生发展核心素养体系，明确学生应具备的适应终身发展和社会发展需要的必备品格和关键能力.在教学中如何将新课程理念与教学实践进行深度融合，如何从知识传授、机械训练、死记硬背向数学学科核心素养、数学能力的培养转变是我们一线教师思考的关键问题.下面结合一道题目谈谈体会.

能这样思考的学生说明已经懂得变通，数学的基本功也很扎实，能灵活调动函数与导数的知识处理问题，但是还需提高思维的层次.这就要求教师在平时教学中有意识地从数学学科核心素养、数学能力的角度去组织教学，引导学生形成学科核心思想方法、核心能力及重要价值观，学会更深入、更创新地去解决问题.

【分析1】这道题跟以前解决过的问题相比，相同点和不同点在哪里？相同点：两个变量，且这两个变量是函数的零点，应该可以化为单变量问题解决;不同点：函数里面有参数a，所证不等式右边是常量，该常数并不是函数的极值点.能否把参数消掉，等价转化为不含参数的问题？

以上四种方法均是为了实现将双变量的不等式转化为单变元不等式，解法1、解法2构造新的函数来达到消元的目的，解法3、解法4则是构造新的变量，将两个旧的变量都换成新变量来表示，从而达到消元的目的.

数学的问题千变万化，教师应立足于课堂，从优化课堂教学入手来破解问题，把数学学科素养的培育与发展作为抓手，在探索中实践，在实践中探索，找到符合教育规律、体现新课标理念要求的学科教育教学方法，从而引导学生在掌握基本知识方法和解题策略的情况下，对新的问题、难题的突破，达到思想方法的领悟、关键能力的提升的目的.

（责任编辑 黄桂坚）