一种基于“移去-恢复”理论的重力数据格网化方法

冯进凯，王庆宾，赵东明，杨 洋，黄子炎，黄 炎

（1. 信息工程大学，郑州 450001；2. 郑州大学，郑州 450001）

重力数据是研究重力场理论和应用的基础。为使用的方便，重力数据一般需要以等经纬度格网的数字形式存储，以格网中点重力值表征网格区域内重力场特征。但在实际测量过程中，实测点通常按照测线方式推进、闭合。而且测量过程中容易受到地形等外界因素的干扰，实际测量数据不一定是格网中点的重力值，这就需要对实测重力点进行格网化，使其按照一定的分辨率等经纬度排列，以利于重力数据的建模和应用[1]。

传统的重力数据格网化的本质是数学拟合，其原理是对已知的离散重力实测数据进行数学内插或外推，从而求得未知点（格网点中点）的重力值。常用的方法有曲面拟合法、反距离加权法[2]、Shepard 拟合方法[3]、Kriging 方法[4,5]以及最近兴起的BP-神经网络和深度学习拟合算法[6]，这些方法从二维数值拟合的角度出发处理重力实测数据，达到了一定的精度，但是这类方法忽略了重力场数据本身具有的物理特性。文献[7]研究表明，由于地球重力场信号的中高频部分和地形之间存在较强的函数关系，在一定范围内，地形数据和重力数据展现出极强的相似性。而且，现阶段全球地形数据已经能达到相当的精度和分辨率，这为利用结合地形数据进行重力数据的格网化奠定了基础。基于此，本文利用重力场数据频谱叠加原理，在顾及重力数据物理特性的基础上结合实验区地形数据，提出一种基于“移去-恢复”理论的重力数据格网化方法，设计出“计算-移去-推估-恢复”的四步重力数据格网化方法（简称“移去-恢复”法），实验结果表明，相比于传统的Kriging 格网化方法，本文提出的方法在精度上有一定的提升，算法稳定性更高，自洽性更好，而且格网化结果能够反映目标区域更多的局部特征。

1 原理和方法

1.1 均衡理论

根据均衡理论[8]，均衡异常应满足浮平衡理论，即均衡重力异常ΔgI理论上应满足如下条件：

其中， Δ g空为空间重力异常，δ gB和 δIC分别为布格改正和地形均衡改正。布格改正δ gB可表示为：

其中，h 为高程， - 0 .1116h 为层间改正，δgTC为局部地形改正。在局部平面坐标系下，局部地形改正计算时，为了兼顾计算精度和效率，通常将积分区域σ 划分为中央区 σ0和远区σ -σ0，中央区采用棱柱积分法，远区采用线性卷积方式逼近真实积分[9]：

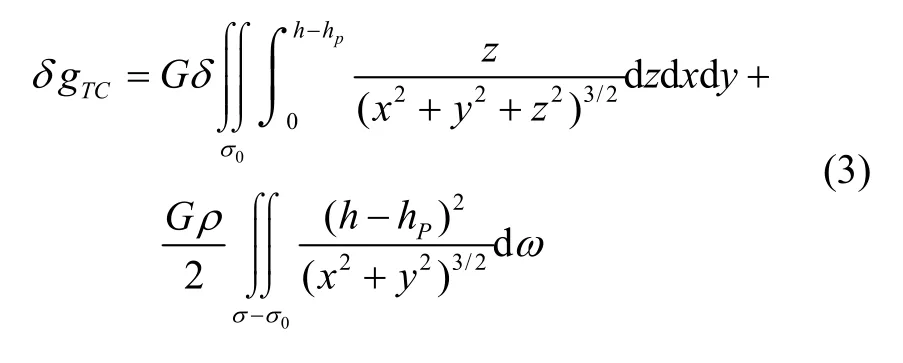
其中，( x , y , z )为流动点平面坐标，G 为万有引力常量，δ 为地球密度常数，h 和 hp分别为流动点和计算点高程。

均衡改正采用较为符合地球实际均衡状态的Airy—Heiskanen 模型[10,11]，该理论认为常密度的地壳漂浮在密度为 ρm的地幔上并保持平衡，超出海平面的部分或低于海平面的部分分别在均衡面以下的部分以“山根”或“反山根”的形式进行补偿。在局部平面直角坐标系下，直接给出均衡改正的计算表达式：

其中，z2=- T，z1=-（ T+t） ，T 为均衡面深度，t 为补偿深度， Δδ 为地壳和地幔部分的密度差，均衡改正计算方法参照局部地形改正。一般来说，空间重力异常变化较为剧烈，在构造高分辨的格网数据时对测点的密度要求较高，而均衡重力异常变化较为平缓，对测点的密度要求较低，比较适合重力点的格网化。

1.2 Kriging 法

Kriging 方法是一种常用的拟合方法，广泛的应用于数据处理以及工程应用等领域，从本质上讲，该方法是利用区域原始数据对估计点进行的最优无偏估计[4,5]。其满足以下条件：

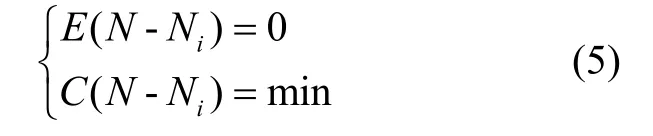
其中，E 与C 代表数学期望与方差，N 与 Ni分别表示计算点与拟合点的大地水准面高。插值模型如下：

其中， λi为每个拟合点的权值。通常利用变异函数代替方差元素：

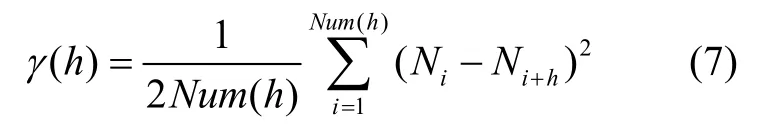
其中，h 表示滞后距，Num(h) 表示滞后距个数，详细推导见文献[5]。

1.3 “移去-恢复”方法

“移去-恢复”理论在局部重力场建模中有着广泛应用[12,13]，基本思想为：根据重力场频谱叠加性原理将重力场信号分为低频、中频、高频三部分，重力场元看作不同频段重力场信号的组合。随着重力卫星技术的发展，低频信号已能达到相当精度，高频和超高频部分主要来自地形起伏影响，可以通过高分辨率的地形数据计算得到。在计算时，移去输入数据的低频、高频信号，对残余值进行建模计算，最后在计算结果中恢复相应频段的重力场信号，即可得到计算点完整频段的重力场元数据[4,14]，其计算步骤可简单概括如下：

（1）首先在重力场元中移除低频和高频频段信息，获得残差重力场元；

其中，L表示扰动位T 的泛函，TRes为残余扰动位，TM和TT分别为低频信号和高频信号。

（2）利用步骤（1）中产生的残差重力场信息结合适当的建模方法进行模型构建；

（3）最后，在计算点中恢复步骤（1）中移去的低频和超高频信息。

需要注意的是，“移去-恢复”过程中，移去和恢复的部分必须是可以在一定的精度条件下精确计算得到的，否则“移去-恢复”过程将无法完成。

同理，公式(1)可改写为如下形式：

空间重力异常可以看作是布格改正、均衡改正和均衡异常三种信号的叠加，从1.1 中可以看出，布格改正和均衡改正均与地形数据相关，可通过地形数据和地壳、地幔密度信息计算得到，符合“移去-恢复”理论的基本前提。现将“移去-恢复”理论应用到重力数据格网化中，基本思路可概括为“计算-移去-推估-恢复”四步，具体计算步骤如下：

（1）计算：根据Airy 均衡理论，利用式(2)-(4)并结合高精度、高分辨率的地形数据和密度信息计算目标区域内布格改正和均衡改正的改正项；

（2）移去：利用式(1)在建模点的空间重力异常中移去地形数据产生的影响（布格改正、均衡改正），得到在建模点较为平滑的均衡重力异常；

（3）推估：利用1.2 中介绍的Kriging 格网化方法对均衡重力异常进行格网化，获取目标点的均衡重力异常数据；

（4）恢复：利用步骤（1）计算的数据，在目标点均衡重力异常的基础上恢复地形数据的影响，即可得到目标点的空间重力异常，公式如下：

2 数值实验

实验区位于南非共和国境内的马塔贝莱高原，范围如图1 所示，实验区内地形变化剧烈，重力场信号复杂，地形数据采用美国国家地球物理数据中心(NGDC)开发的Etopo1 的1′分辨率格网化地形数据[15]，实验区内最大高程落差 2334 m，平均高程1052.2284 m，选用离散点所在地形格网为离散点高程，顾及地形改正和均衡改正边界效应，选取图1 红框部分为中心计算区域。从“GRAVCD-africa”数据集中搜集到计算区1789 个实测空间重力异常数据（图1 中三角点和圆点），地形数据和实测点空间重力异常数据统计信息见表1。

图1 实验区域高程及点位分布示意图Fig.1 Elevation and points distribution of the experimental area

表1 高程和实测点空间重力异常统计表Tab.1 Statistics table of free-air gravity anomaly and elevation

为验证本文所提方法的正确性，随机选择计算区内894 点为建模点（圆点），其余895 个点为检核点（三角点），设计如下对比实验：

方案一：直接格网化方法，利用传统的格网化方法直接对实验区内的建模点进行数据格网化，格网化时采用物理大地测量学中常用的 Kriging 插值方法[17,18]，其为区域原始数据对估计点进行的最优无偏估计。利用离散建模点位置信息和空间重力异常得到检核点空间重力异常数据，最后和检核点实测数据进行对比，从而得到本方案的格网化精度；

方案二：利用本文提出的“计算-移去-拟合-恢复”格网化方法，并结合实验区高精度、高分辨率的地形数据和密度信息构造计算区域的均衡改正、地形改正和层间改正项，在建模点移去各项改正，得到建模点均衡重力异常，利用Kriging 格网化方法将实验区格网化均衡异常格网化；最后根据点所在网格恢复移去项（均衡改正和布格改正），得到检核点空间重力异常，并和检核点实测数据进行对比，分析格网化精度。

2.1 方案二各类改正项分析

方案二“计算”步骤中，均衡面深度选为40 km，地壳密度为2670 kg/m3，岩浆密度为3270 kg/m3，地形改正积分半径选取30′，利用以上数据分别计算出中心区域地形改正、均衡改正和层间改正，计算结果见图2、表2。

图2 计算区各项改正示意图Fig.2 Diagram of various corrections

表2 各项改正统计表/mGalTab.2 Statistical table of all types of corrections/mGal

分析图2 可以发现，在计算区内地形改正、均衡改正和层间改正的分布和地形趋势基本一致，相似度极高，而且计算区内任何位置的改正项均可以通过严密公式和高分辨率的地形数据以及地壳密度项计算出来，符合“移去-恢复”理论的基本条件。

方案二“移去”过程中，依次移除建模点空间重力异常中的布格改正、均衡改正，分别得到布格重力异常和均衡重力异常，统计信息见表3，绘制如下，见趋势图3（为方便对比，图中数据消除均值）。

图3 “移去”过程趋势图Fig.3 Diagram of “Remove” process

表3 建模点各项重力异常统计表/mGalTab.3 Statistics table of all types of gravity anomaly/mGal

从图3 中可以看出，在空间重力异常中依次加入布格改正和均衡改正后，建模点的重力异常信号变化由原来的23.93 mGal 衰减为12.8662 mGal，差值阈由原来的140.3415 mGal 减小为78.8301 mGal，毛刺点明显减少，变化趋势更加平滑，所以空间重力异常在经过布格改正和均衡改正后更适合目标点的格网化，数据处理过程中的误差将会减小。

2.2 不同格网化方法精度分析

按照方案一和方案二组织对比实验，统计两个实验方案的结果于表4，差值见图4。

图4 两种方法各点差值示意图Fig.4 Diagram of the differences between the two methods

表4 两种方法差值统计表/mGalTab.4 Statistical table of differences between two methods/mGal

实验结果证明，无论哪种方案均能以一定的精度推估未知点的空间重力异常，其中方案一从数学角度建立已知点和未知点的联系，进而根据建模点的空间重力异常推估出检核点空间重力异常，检核精度为5.5168 mGal；方案二在数学格网化的基础上顾及了地球自身的物理信息，拟合精度为3.9996 mGal，相比于方案一，精度提升了27.5%，从精度上来看，本文提出的方法更优。“移去-恢复”法计算结果差值最大值和最小值相比传统方法均有了一定的收敛，阈值缩小近一倍。从图4 中看，方案二各检核点差值分布更加集中，误差分布更加均匀，粗差点更少。这是由于“移去-恢复”中在纯数学拟合中加入了地球的物理信息，整体拟合趋势和重力数据分布趋势更加符合，拟合精度更好，差值分布更收敛，残差值波动也更小。

根据以上两种实验方案，利用计算区内全部的1789 个重力实测数据作为建模数据，构造出计算区内1′分辨率的空间重力异常，得到实验结果如图5 所示，再将1789 个建模数据作为检核数据验证算法的自洽性，统计结果见表5 和图6。

图5 两种方法构造的区域重力异常图Fig.5 Regional Free-air gravity anomaly constructed by two methods

图6 和表5 表明，本文提出的“计算-移去-推估-恢复”方法自洽性检核的各项数学统计指标均优于直接推估方法，精度更高，系统差更小。而且在图5 中可以看出，“移去-恢复”法所构造的局部空间重力异常包含更多的细节特征，细部信息刻画更为详细。这是 因为传统的数学推估方法在计算时，会损失数据中原有的高频信号，推估结果较为平滑；本文所提方法在“移去-恢复”的过程中，充分考虑了地形数据的影响，补齐了实验区内空间重力异常的高频项，使得重力场元的频段更加完整。

图6 两种方法自洽性差值示意图Fig.6 Diagram of self-consistent error by two methods

表5 两种方法自洽性误差值统计表/mGalTab.5 Statistics table of self-consistent error by two methods/mGal

3 结 论

本文将“移去-恢复”理论应用到局部重力数据格网化中，在格网化过程中加入地形数据和密度信息，将传统的纯数学拟合转化为顾及地球物理场信息的格网化，通过实验区实测数据对比实验，得到如下结论：

（1）实测空间重力异常较为“毛糙”，直接对其进行数学拟合时，过程性误差较大；在消除掉布格改正和均衡改正后数据变得平滑，有利于重力数据的格网化；

（2）实验区内，“移去-恢复”方法构造的目标区域空间重力异常精度相比于Kriging 格网化的精度更高，差值波动范围更小，而且能够描述实验区内重力场的细节特征，重力场元的频段更加完整；

（3）“移去-恢复”方法利用地形数据将变化剧烈的空间重力异常转化为较为平滑的均衡重力异常，然后再进行数据处理。可以预测，当目标区域内实测重力数据较少时，“移去-恢复”结合高分辨率地形数据方法的优势将更加显著。