浅谈数形结合思想在小学数学课堂教学中的应用

陈国菊

中图分类号：A 文献标识码：A 文章编号：（2021）-35-474

数学是一门高度抽象、逻辑性很强的学科，而小学阶段的学生思维发展水平还不够成熟，对于有些抽象的学习内容要通过直观的画图学生才容易理解。在小学数学课堂中应用数形结合就可以帮助学生把抽象的、难理解的问题变得简明、形象，使学生易于接受和理解，来提高学生的学习兴趣和激发他们对数学学科的热爱，为今后学习数学奠定基础。

一、应用数形结合有助于提高学生的学习兴趣。

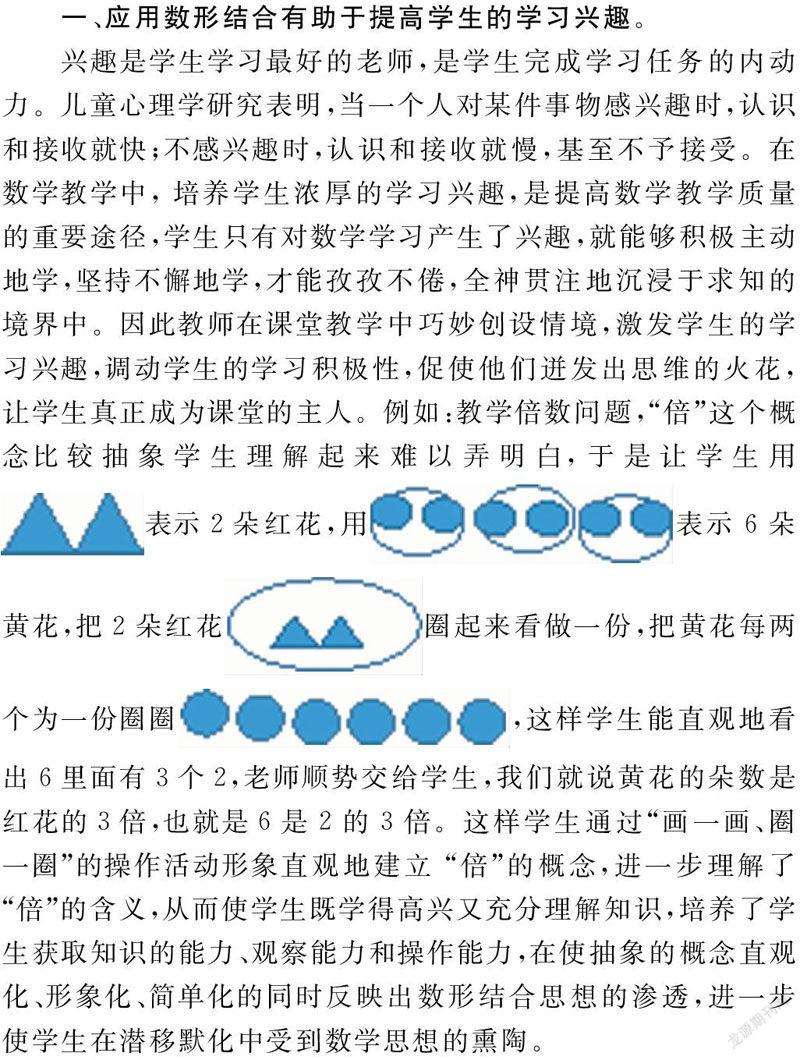
兴趣是学生学习最好的老师，是学生完成学习任务的内动力。儿童心理学研究表明，当一个人对某件事物感兴趣时，认识和接收就快;不感兴趣时，认识和接收就慢，基至不予接受。在数学教学中，培养学生浓厚的学习兴趣，是提高数学教学质量的重要途径，学生只有对数学学习产生了兴趣，就能够积极主动地学，坚持不懈地学，才能孜孜不倦，全神贯注地沉浸于求知的境界中。因此教师在课堂教学中巧妙创设情境，激发学生的学习兴趣，调动学生的学习积极性，促使他们迸发出思维的火花，让学生真正成为课堂的主人。例如：教学倍数问题，“倍”这个概念比较抽象学生理解起来难以弄明白，于是让学生用表示2朵红花，用表示6朵黄花，把2朵红花圈起来看做一份，把黄花每两个为一份圈圈，这样学生能直观地看出6里面有3个2，老师顺势交给学生，我们就说黄花的朵数是红花的3倍，也就是6是2的3倍。这样学生通过“画一画、圈一圈”的操作活动形象直观地建立 “倍”的概念，进一步理解了“倍”的含义，从而使学生既学得高兴又充分理解知识，培养了学生获取知识的能力、观察能力和操作能力，在使抽象的概念直观化、形象化、简单化的同时反映出数形结合思想的渗透，进一步使学生在潜移默化中受到数学思想的熏陶。

二、应用数形结合有助于激活学生的思维

苏霍姆林斯基说过“孩子的智慧在手指上”。学生在解决数学问题的过程中利用画图这个中介辅助理解题意，在画图的过程中来展示其数学思维过程和思维火花。把一些稍难的数学题目“翻译”成图形，即把文字转成图形，并将图形转成思维，是一个从“外化”到“内化”来发展学生逻辑思维的过程。若在教学过程中巧用“画图”，能将教学内容化静为动，引导学生在感性认识中发展智力，从而培养学生的思维能力。例如：在教学用假设法解决问题时，出示题目：小汽车和摩托车共24辆，86个轮子，问小汽车、摩托车各有多少辆？让学生用算术方法解决这类问题不能完全理解，用方程解决有的学生不会解方程，用表格和一一列举又太麻烦，于是借助画图，一步一步总结方法和规律，先画24个长方形表示24辆车，假设全是摩托车，给每个长方形画上2个轮子，共画了48个轮子，还剩86-48=38（个）没有画上，问为什么有剩下的轮子？学生很直观的看出把汽车看成摩托车，这样每辆汽车少画4-2=2个轮子，所以轮子有剩余。再把剩下的轮子添上，每个长方形还可以添2个，38个轮子可以添38÷2=19（辆）。从画好的图中可以看出，有4个轮子的19辆是小汽车;只有2个轮子的5辆是摩托车。学生借助画一画，从图形中直观地看出问题的答案，并能够从中建立解决这类题目的模型思想。借助数形结合将文字信息与学习基础结合，做到以画促思，化抽象为直观，有效地帮助学生解决问题，提高学生解题能力，同时感悟数形结合的价值。使得学习得以继续，思维发展有了凭借，数学学习的思想方法真正得以渗透。

三、应用数形结合有助于帮助学生理清数量关系答疑解难。

对许多学生来说，学好数学最大的阻碍是应用题。数学解决问题的教学核心是是理清数量关系，问题的求解在于通过对情境的理解，掌握数量关系，从而建立解题模型。有不少应用题文字叙述较为抽象，数量关系复杂。如果老师总是从字面去理解题意，用言語来表述数量关系，即便老师讲得声嘶力竭，学生仍很难理解掌握;即便学生理解了，也只限于会做某个题。而数形结合能够让学生用图示来表述抽象的数学问题，把抽象的数学问题具体化，帮助学生理解题意分析数量关系，使学生容易理解与掌握，提高解决问题的能力。让学生体会到在数学学结合的作用，为解决应用题指明了方向，时时吸引学生爱上数学，让学生在画图中愉悦的寻找办法解决问题。

如，在教学“稍复杂的分数应用题”时，首先让学生结合情境找出数学信息并提出数学问题：西藏的布达拉宫规模宏大，它东西长360米，比南北长1/5。南北长多少米？让学生自主探究画出线段图，结合线段图分析数量关系，

引导学生根据线段图，结合题中的分率句，容易找出数量关系式：

南北长+东西比南北长的长度=东西长;南北长Χ（1+1/5）=东西长。这样学生借助直观的图示，将题目中隐含的数量关系以形象直观的形式体现出来，达到解决问题的目的，看来画图法的确是教学中行之有效的办法，在教学中有意识的培养学生画图的意识和能力，它既促进了学生思维的发展，又培养了学生解决问题的能力，收到事半功倍的效果。学生在解决完问题后，要引导他们意识到画图法在分析题意中的作用，启发学生在以后的解题中自然然而的使用。

可见数形结合，不但是数学解题策略中最基本的、也是一个很重要的策略。数形结合，其实质是将抽象的数学语言与直观的图形联系。总之，数形结合策略贯穿于整个小学数学解决问题的教学中。教师在教学的过程中要善于利用、多加引导、适时渗透，使学生掌握“数形结合”策略的数学技能，逐渐具有应用有效策略的自觉性，形成良好的思维习惯，促使学生做到心中有图见数、有数见图，正如数学家华罗庚说的：“数缺形时少直观，形少数时难入微;数形结合百般好，隔离分家万事休。”提高学生灵活运用策略解决实际问题的能力，拓展学生的思维力，提升数学思想方法。