一类两正幂指数大小比较问题的多种解法
张 辉,方晓峰
(火箭军工程大学 基础部,陕西 西安 710025)
0 引言
导数的应用[1]125-180是一元函数微分学的重要内容和难点知识,而利用函数导数的正负判定函数的单调性进而判定两个数的大小关系是一个常见的问题。在我校2020年秋季学期高等数学(上册)的期终考试中,就出现了一道判定两个正幂指数的大小问题,具体为:若0 一般情形下,判定两个正数的大小关系的方法有两种,一种是研究这两个正数之差与0之间的大小关系,一种是研究这两个正数之比与1之间的大小关系。在此过程中常常需要构造辅助函数利用函数的单调性来判定两个函数值的大小关系。对于此问题,可以首先构造辅助函数f(x)=xa-ax,a≤x≤b,则有f(a)=0,f(x)在闭区间[a,b]上连续,且当a 解法1当a=1时,显然有ab=1=a 通过上述分析可以发现,即使是同一个解题思路和方法,构造不同的辅助函数也导致求解过程和计算工作量大大不同。因此,需要同学们在求解问题中,一般构造便捷有效的辅助函数来求解问题,达到事半功倍的效果。 事实上,此类问题是判定两个正幂指数的大小关系,对于幂指数往往可以通过取对数进行变形简化研究,因此也可以采用解法2来求解。 解法2因为对数函数lnx为严格单调递增函数,所以比较ab和ba的大小关系就等价于比较lnab和lnba的大小关系,即比较blna和alnb的大小关系。现考虑alnb-blna与0的大小关系。 从上述求解过程可以看出,此种方法不需要证明函数a-xlna在开区间(a,b)内取值大于0这个重要结论,也就是说比第一种方法简单一些,因此推荐此解法的第二种方法。 在解法2和解法3中,我们是利用对数函数的单调性通过取对数进行恒等变形进行分析研究的,而幂函数也同样具有一致的单调性,这也为我们提供了一种求解思路和方法,于是可得解法4。 在解法2、3和4中,我们是利用对数函数和幂函数的单调性通过恒等变形进行分析研究的。而指数函数也同样具有一致的单调性,这同样也为我们提供了一种新的求解思路和方法,于是可得解法5。 解法5当a=1时,则有ab=1=a 下面分两种情形讨论分析,当0 需注意的是,上面构造的辅助函数只含有a并不含有b,求解过程较为复杂。若构造另一个辅助函数只含有b并不含有a,其求解计算量是否会减少呢?以下给出详细的求解过程。 当b=1时,则有ba=1=b>a=ab。 当b≠1时,因为ab=bblogb a和指数函数bx为严格单调函数,所以比较ab和ba的大小关系就等价于转化为比较blogba和a的大小关系。 从上述求解过程可以看出,此种方法不需要证明函数a-xlna在开区间(a,b)内取值大于0这个重要结论,也就是说比第一种方法简单一些,因此推荐解法5的第二种方法求解。 以上我们利用5种方法分析判定两正幂指数的大小关系,通过比较可以发现,解法3是较为简单的方法,但这种方法需要进行一些恒等变形并不容易会想到。值得注意的是,我们所给出的研究问题是可以进行简化的。事实上,当a=1时,则有ab=1=a 事实上,对于两个正幂指数ab和ba的大小关系,有一般性的结论: 1)当0 2)当e≤a 3)当a 图1 函数的图形Fig.1 Curve of the function 本文研究了两正幂指数ab和ba的大小关系的判定问题,利用5种方法进行了分析讨论,旨在为大一学生对如何利用函数的导数判定两个数的大小关系的解法有更深的理解和掌握,进而对导数的应用[2-6]有更深入的理解。对于大一学生而言,关键是如何针对具体问题寻找便捷有效的方法解决问题,这也是大一学生在学习过程中需要着重提高的环节,进而达到事半功倍、举一反三的效果。1 5种解法

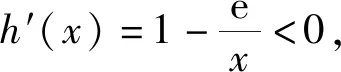



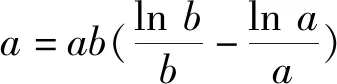
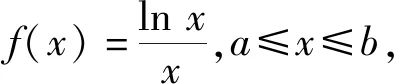

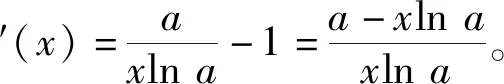


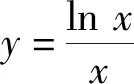
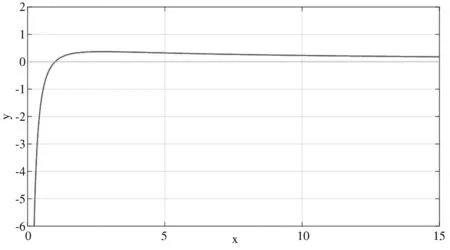
2 小结

