基于前馈神经网络的预测分类器

黄丽婷

（泉州信息工程学院软件学院，福建 泉州 326000）

0 引言

深度学习经历长时间的发展而孕育出各种各样的人工神经网络技术[1]。就像人类要想成为一个好的决策者可以通过经验进行学习，人工神经网络也可以通过对数据的学习而成为一个好的分类器。

在深度学习中，虽然人工神经网络看起来很复杂，其节点、层数和参数的数量繁多，但神经网络的核心组件只有层、模型、损失函数和优化器这四个部分。此外，在深度学习实际项目中，为了让人工神经网络模拟人类的学习行为，需要提供大量数据样本。在此之前，还需要对数据样本进行预处理工作，这一系列的前置工作必不可缺[2]。

深度学习领域的技术框架主要为Keras和PyTorch，其中Keras是Python中的高级深度神经网络API，它基于Tensorflow、CNTK或Theano框架运行[3]。而另一种主流的深度学习框架Pytorch虽然晚于Keras出现，但其发展十分迅速。PyTorch 1.0版本不但优化了原有内容，并且整合了Caffe2而成为十分热门的深度学习框架[4]。

近年来，深度学习中的各类人工神经网络模型已被大规模应用于人脸检测、物体检测、语音识别、机器翻译、自动驾驶等各种各样复杂的任务[1]，而深度学习在医疗领域的应用也是日新月异。随着可用于机器学习的医疗领域数据（如WHO全球卫生观察站数据）被大量公开于网络，大量医疗数据都可以通过网络下载而获取，这为医疗领域的深度学习模型研究开发提供了必要的大数据基础。

在对医学数据分析和疾病的识别与预测上，深度学习的计算模型也具有十分重要的应用意义，例如：对于骨质增生、椎间盘突出、脊椎滑脱等具有大量患者的骨科疾病，深度学习的计算模型可以为这些疾病的分类、识别和预测提供高效的参考信息。

1 前馈神经网络

机器学习中的人工神经网络（ANN）是模仿人脑的生物神经网络结构来进行构建，它具有节点且节点间具有内部连接的计算网络。其中的节点被编程为具有相似于真实神经元的表现，因而被称为人工神经元。[1]

深度学习则是在机器学习的基础上建立一套更为复杂的人工神经网络模型，其中的一种经典模型叫作前馈神经网络（feedforward neural network）[5]，它可以让计算机通过较为简单的概念来构建复杂的模型。前馈神经网络的本质是一种数学函数，它能将一组输入数据映射成输出数据，这样复杂的函数是由许多较简单的函数复合而成[4]。

例如，有三个函数 ，他们复合在一起形成如下函数。

式中，f(1)代表深度前馈网络的输入层；f(2)代表深度前馈网络的隐藏层；f(3)代表深度前馈网络的输出层。这个例子描述了一个最简单的前馈神经网络模型，而更为复杂的前馈神经网络往往具有多个隐藏层，这些隐藏层的维度决定了神经网络的宽度。

一个多维的前馈神经网络往往由输入层xi、隐藏层hnj和输出层yk构成（其中hnj的下标n为隐藏层数量，而下标j为第n隐藏层的神经元数量）。在前馈神经网络中，其隐藏层和输出层的输入张量都需要通过线性函数来进行计算。对于第n隐藏层的第j个神经元来说，假设其输入张量的数量为i，那么其相应的输入线性函数f(nj)（x）如下所示。

该函数f(nj)（x）是典型的线性回归函数[6]，其中xi为输入层张量，而wij则代表不同层神经元之间的连接权，wij也是模型需要通过训练来学习的参数。然而，在计算该神经元的输出值时，前馈神经网络则采用非线性函数来进行计算。在隐藏层和输出层中，所有的神经元都必须采用非线性的激活函数来计算其输出值。例如，对于第n层隐藏层上的第j个神经元，其激活函数可以表示为以下公式。

如该公式所示，隐藏层上的任何一个神经元的输入值为：f(nj)(x)与阈值θnj之间的差值，该差值将作为变量被代入激活函数中来计算其输出值，例如，第n层隐藏层上的第j个神经元的输出值也正是其激活函数的计算结果。

而输出层yk上的神经元，采用与隐藏层神经元类似的算法来对其输入值和输出值进行计算。就前馈神经网络的分类器而言，输出层神经元的输出值y=f（*）（x）代表着输入层的张量通过前馈神经网络模型而被映射成某一个类别y。

而在模型训练中，作为分类器的前馈神经网络一般采用监督学习的方式，即使用有标签的数据集来训练模型。在监督学习的过程中，首先要设计深度学习的静态结构，如构建前馈神经网络模型、选择训练需要的损失函数和优化器等。在此基础上，模型的训练还包括一系列动态的实现过程，如预处理数据集、前向传播、反向传播和优化模型等。

1.1 静态结构

运用前馈神经网络构建分类器时，必须设计好以下静态结构。

（1）层（Layer）：设计输入层、隐藏层和输出层的神经元结构。

（2）模型（Model）：设计由层构成的运算模型，先设计好每一层的输入线性函数，也即预设连接权wij等的初始值；然后，选择隐藏层hnj和输出层的激活函数；对于分类器模型，softmax函数或是ReLU函数都可以作为激活函数。

（3）损失函数（Loss Function）：用于计算模型的预测值与真实数据之间的误差，如均方差函数和分类交叉熵函数；分类器往往采用交叉熵函数计算损失；如基于N个样本数量和M种输出类别，其交叉熵损失函数L如下所示。

（4）优化器（Optimizer）：使损失函数误差值最小化的算法，好的优化器能迅速通过损失函数学习到适合的连接权w 和阈值θ ；常用的优化器有随机梯度下降算法（SGD）和自适应优化算法等[8]。

1.2 实现过程

在实现前馈神经网络模型的过程中，还必须包括以下执行步骤。

（1）预处理数据（Preprocess Data）：载入相关数据集，根据评估方法对数据集进行划分，例如根据留出法（Holdout）将数据集分为训练数据和测试数据。

（2）定义模型（Define Model）：根据前馈神经网络的静态结构来逐层定义神经元数量、激活函数，以及输出层神经元对应的预测分类标签。

（3）构建/编译模型（Compile Model）：根据所定义的模型，初始化连接权值，并指定损失函数、优化器和评估度量。

（4）前向传播（Forward Propagation）：在将输入值xi运算成输出值y 的过程中，数据在网络上向前传送；输入值 xi提供初始数据，并通过模型层层传递，经过每一层隐藏层的运算，最终在输出层上输出为预测类型y。

（5）反向传播（Back Propagation）[9]：也被称为误差逆传播，是指将输出值的误差反向传递给隐藏层的神经元，这些误差数据可以通过优化器来帮助优化隐藏层神经元的相关参数，优化的内容包括模型的连接权w和阈值θ。

（6）模型评估（Model Evaluation）：对于已经完成训练的分类器模型，可以使用预先设置的测试数据集来对其进行测评，以测试分类器的准确率。

（7）可视化结果（Visualization）：对于神经网络的模型结构、训练过程和评估结果，使用可视化工具以图像的形式进行展示。

2 实验及其结果

2.1 实验环境

本实验的开发环境如下所述。

（1）操作系统为macOS Catalina 10.15.6系统。

（2）集成开发环境为Anaconda Navigator 1.9.12中的Spyder 4.1.5。

（3）开发框架为基于Tensorflow 2.0的Keras深度神经网络框架。

2.2 实验数据集

本实验所采用的骨科患者生物力学特征数据集的原始数据集来自UCI ML存储库（http：//archive.ics.uci.edu/ml），其后经Kesci数据平台整理而形成CSV格式文件。

在该数据集中，每个患者的疾病特征由如下的骨盆和腰椎的形状和方向（每个为一列）所派生出的6个生物力学属性表示。

（1）pelvic incidence：骨盆入射角

（2）pelvic tilt：骨盆倾斜

（3）lumbar lordosis angle：腰椎前凸角度

（4）sacral slope：骶骨倾斜角

（5）pelvic radius：盆腔半径

（6）grade of spondylolisthesis：脊椎前移的等级

在该数据集中，每个患者的疾病数据分类则有以下三种情况。

（1）Hernia：椎间盘突出

（2）Spondylolisthesis：脊椎前移

（3）Normal：正常

2.3 实验模型设计

基于以上前馈神经网络的理论，本文为具有6个输入特征数据和3个输出分类数据的预测分类器设计了如图1所示的前馈神经网络模型。

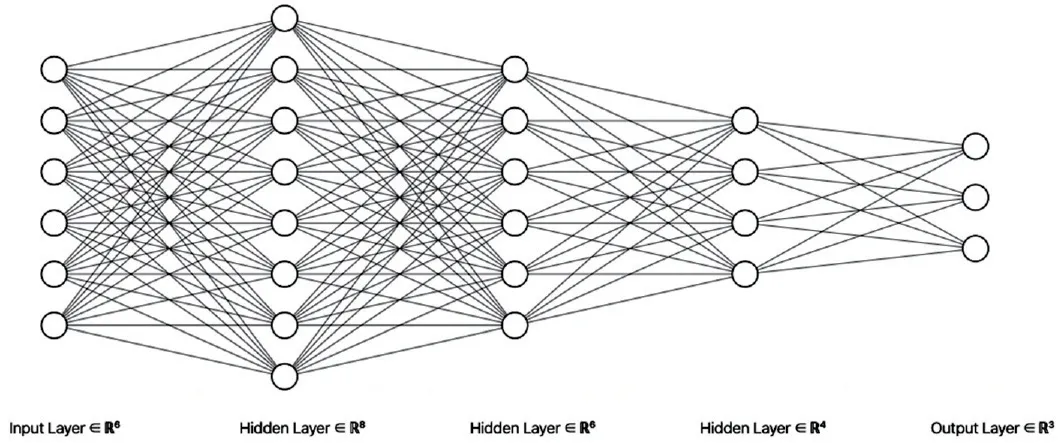
图1 分类器模型

在该模型中，输入层（xi）有6个输入神经元，对应骨科疾病数据集中的6个生物力学属性；而输出层（yk）有3个输出神经元，对应骨科疾病分类。它们之间存在3层隐藏层（hnj），这3层隐藏层分别具有8个神经元（h11～h18）、6个神经元（h21～h26）和4个神经元（h31～h34）。

在该模型中，所有的初始连接权在[-1，1]的范围内通过正态分布初始化获取。其隐藏层的激活函数是ReLU函数（线性整流函数），而输出层则采用softmax函数作为激活函数，它们的具体公式和输出值范围如表1激活函数所示。

表1 激活函数

本文将通过实验来对该分类器模型进行训练，在实验中，将采用不同的优化器来比较其反向传播的收敛速度，并通过最终模型的准确率来确定最高效的优化器。

2.4 实验实现方案

本实验具体实现方案如表2所示。

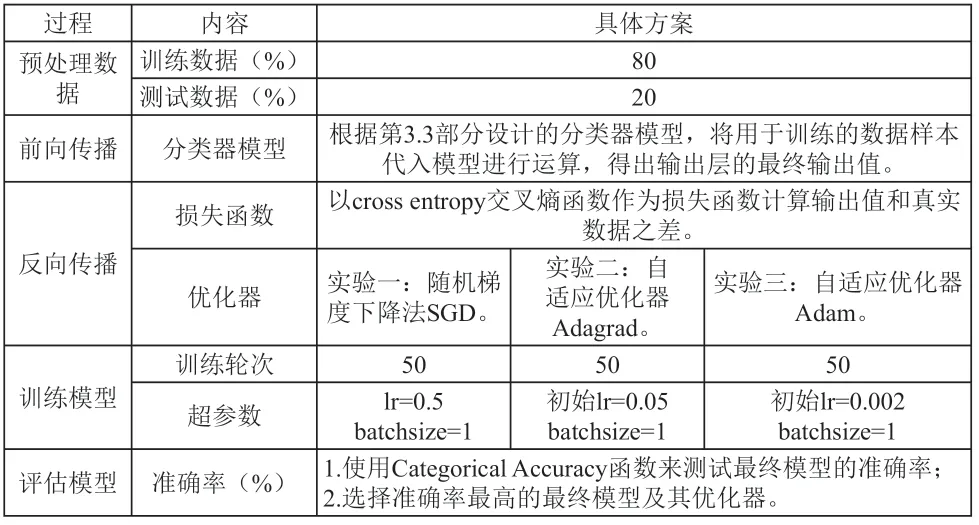
表2 实验方案设计

2.5 实验结果分析

图2、图3和图4分别展示了实验一、实验二和实验三的模型训练过程和评估模型时的准确率。

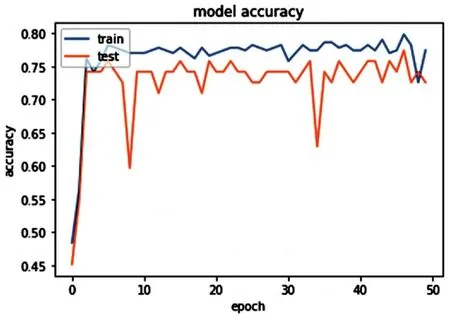
图2 SGD优化器

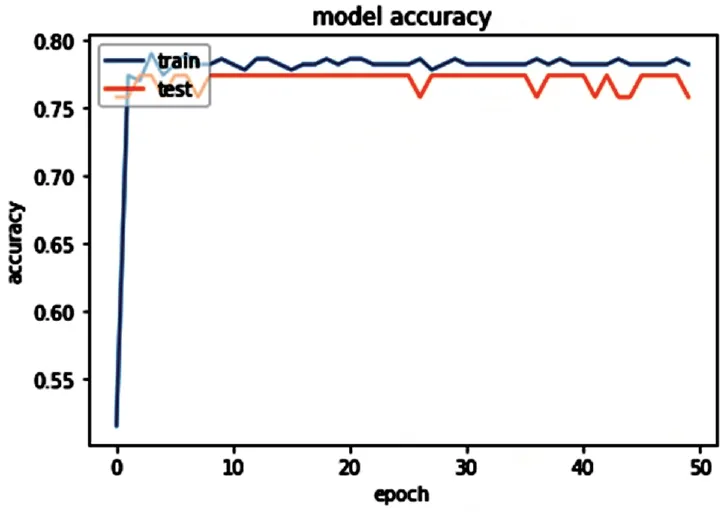
图3 Adagrad优化器

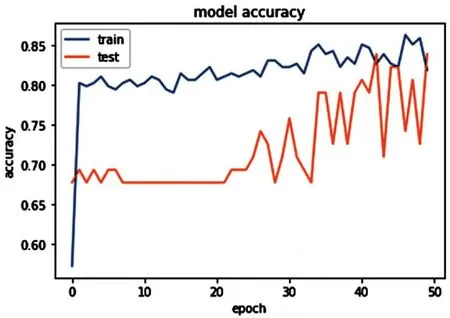
图4 Adam优化器

从以上三张图所示的实验数据可以看出，虽然收敛最快、最稳定的优化器是Adagrad，但是其评估（test）准确率比训练（train）准确率更低，而其中训练结果准确率最高的优化器是Adam。这两种自适应优化器的效率都比没有经过参数精调的SGD优化器更好。

使用这三种不同优化器进行模型训练后，在评估时的损失值和准确率如表3所示。

表3 实验损失值和准确率

从以上结果可以看出，在优化该分类器模型时，Adam相比其他两种优化器的训练结果，其评估准确率更高，达到83.87%，对于疾病分类具有较鲜明的参考作用。

3 结束语

本文基于深度学习中的前馈神经网络理论，选取了骨科患者特征数据集来进行分类预测的实验。在实验中，本文设计出一种基于6个输入神经元和3个输出神经元的分类器模型，该模型包含3层隐藏层。本文使用骨科患者特征数据集来对模型进行训练，并对模型的分类预测结果作出了评估。根据实验结果，最终确定使用Adam优化器来进行模型优化，这为创建更高效的疾病分类器提供了参考。

本文只针对骨科疾病数据进行了预测分类实验，今后在此基础上将根据不同领域的数据分类需求而对分类器模型提出多种设计并进行对比实验，将尝试对比分析不同维数的前馈神经网络对于各领域数据分类预测的准确率。