基于残高控制的深槽插铣工艺参数多目标优化*

徐卫宏， 宋伟伟， 陈伦旺， 黄 涛， 张小明

（1.中国航发南京轻型航空动力有限公司，南京 210000；2. 陆军装备部航空军事代表局驻上海地区航空军事代表室，上海 200233；3. 华中科技大学，武汉 430074）

槽铣加工广泛应用于汽车、航空航天、医疗等行业，其一般流程为先粗加工，再半精加工，最后精加工，直到工件表面质量满足粗糙度要求。常规铣槽粗加工方式是利用平底铣刀，以槽中心线直接下刀一定深度并侧铣一定长度，再重复该过程直到加工到规定的深度。但当槽的深度较大时，刀具悬伸量大，刚性变差，受到的径向力会使其径向振动，影响刀具寿命和加工质量[1]。插铣法采用底刃切削、轴向进给，如图1[2]所示。相比于常规铣槽方式，插铣刀受到较大的轴向力和较小的径向力，减小了刀具的径向振动，适用于薄壁和非薄壁零件的加工，且有更高的加工效率。

在槽铣加工方面，Sheikh–ahmad等[3]基于机械力学模型，提出了槽铣出口毛刺尺寸的预测算法。Danis等[4]研究了不同前角的切削力行为，并估计了基于切削力分解的摩擦系数。Niknam 等[2]研究了切削参数和刀刃边缘半径对插铣刀受到切削力的影响，并指出粗加工时的残余高度会影响精加工过程，而精加工时的残余高度影响工件的加工质量。Monies等[5]建立了深槽插铣的机械力学模型，并探讨了刀具不同几何形状对切削力的影响。

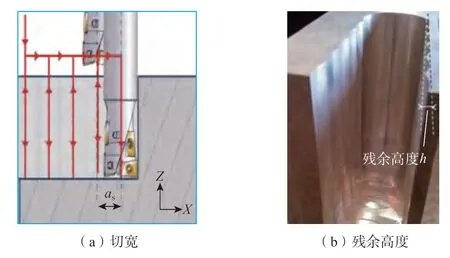
图1 深槽插铣加工示意图Fig.1 Schematic diagram of deep groove plunge milling

在残余高度控制方面，朱虎等[6]指出步距越大，残余高度越大，表面加工质量越差，但材料去除率越高。丁东旭等[7]提出了动态刀具补偿技术的残余高度算法，保证了工件表面加工质量。刘一波[8]基于一次残余高度进行二次铣削轨迹优化，明显降低了表面粗糙度。Kukreja 等[9]提出了从仿真软件获取的CAD 模型和CNC 刀具路径中生成残高点两种方法，估算了自由曲面加工中的残余高度，解决了实践中残高评估较难的问题。现有的残余高度控制研究，主要集中在球头铣刀的精加工中，从而提高表面加工质量。

为了解决实际生产中工艺参数选取困难的问题，众多学者针对插铣工艺参数优化做了很多研究。程耀楠等[10]采用经验公式建立切削力模型，以材料去除率和切削力为优化目标，采用加权法建立目标函数，优化了工艺参数。Zhuang 等[11]提出了小切宽插铣切削力的机械力学模型，并在稳定性约束条件下，以最大材料去除率为优化目标，对切削宽度、侧向步距、每齿进给量和主轴转速4 个切削参数进行了优化。冯新敏等[12]以材料去除率和切削力为优化目标，运用模糊分析法对切削参数进行优化。翁剑等[13]引入机器学习方法建立切削力模型并与传统经验方式比较，最后以材料去除率和切削力为优化目标，优化了工艺参数。

目前有关工艺参数优化的研究，主要集中于以切削力和材料去除率为优化目标，对小切宽插铣工艺参数进行优化。而在深槽插铣加工中，除了切削力和材料去除率等性能指标，残余高度对后续精加工次数以及表面加工质量都有着重要的影响。因此，本研究针对深槽插铣过程，以最大材料去除率和最小残余高度为优化目标，采用比值加权法建立目标函数，提出了一种切削力约束和稳定性约束下的工艺参数优化模型。

槽铣切削力模型

切削力对切削过程有着重要的影响，不仅是机床、刀具设计的重要依据，也是工艺系统变形和振动研究的重要基础。切削力仿真的经典方法是通过大量切削力数据代入经验公式进行回归分析求解系数，进而预测平均切削力。但经验公式法无法预测瞬时切削力及其变化规律，因此本研究采用Zhuang 等[14]提出的机械力学模型来预测插铣切削力，不仅可以预测每个刀具周期内瞬时切削力的变化规律，也可以计算最大切削力。

可转位插铣刀由于刚度高、刀杆长，常用于槽铣加工中。图2 为可转位插铣刀几何示意图，D为刀具直径；L为切削刃长度；Ψr为刀齿前角；Ft为与瞬时切削速度相反的切向力；Fr为指向刀具轴心的径向力；Fa为与刀具进给方向相反的轴向力。图3 为插铣刀槽铣加工的切削几何示意图，O1为前一个切削位置的刀具中心；O2为当前切削位置的刀具中心；A为前一刀具位置的切入点；B为当前刀具位置的切出点；阴影部分为当前位置的切削面积；h为两个切削位置之间的残余高度。

根据图3 中刀具当前位置和前一刀位置的几何关系，以X轴负半轴为基准，第j个刀齿在t时刻的瞬时切削宽度为：

其中，φmin为当前位置刀具切入角度；φmax为当前位置刀具切出角度，如下：

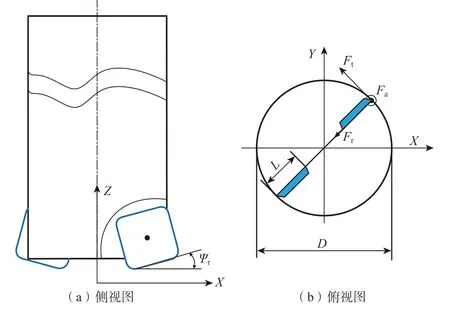
图2 可转位插铣刀几何示意图Fig.2 Geometry diagram of indexable plunge milling cutter

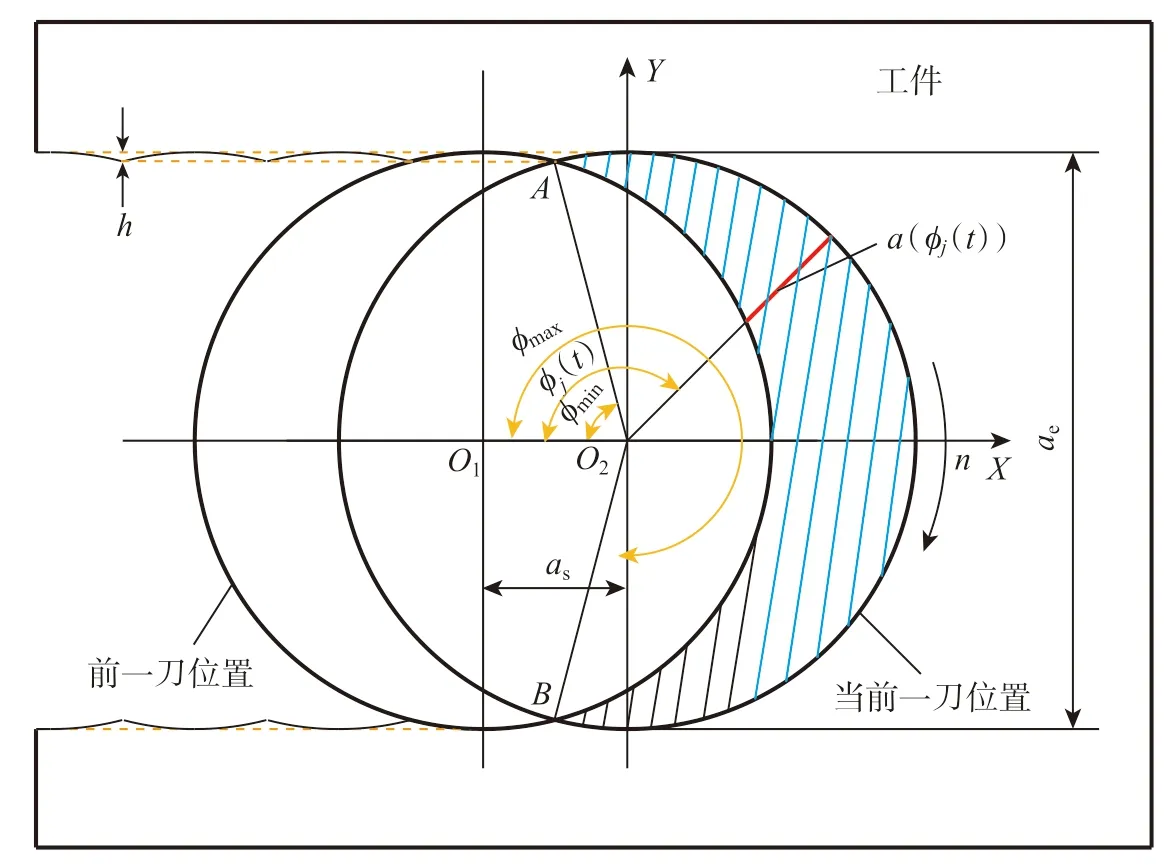
图3 槽铣切削几何示意图Fig.3 Schematic diagram of slot milling cutting geometry

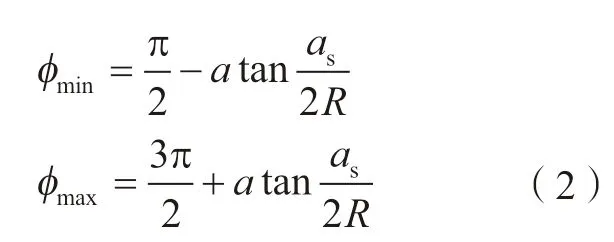
假设切削力的大小与瞬时未变形切屑的横截面积呈正相关性，则切向切削力、径向切削力、轴向切削力可分别表示为动态变化切削面积的函数：

其中，Kt、Kr、Ka分别为插铣加工的切向力系数、径向力系数和轴向力系数；φj（t）表示以X轴负轴为基准，刀具第j个刀齿在t时刻的位置角可表示为：

其中，n表示主轴转速；φp=2π/N表示齿间角，N为刀齿个数。

将动态切向力、径向力、轴向力通过坐标变换，得到直角坐标系下的三向切削力为：

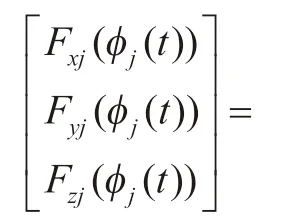
求出单个刀齿的三向切削力之后，再对某一时刻的角度下所有刀齿的切削力进行求和，可以得到刀具瞬时动态切削力。

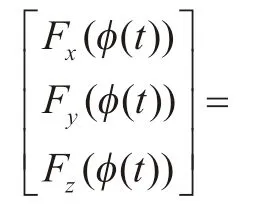
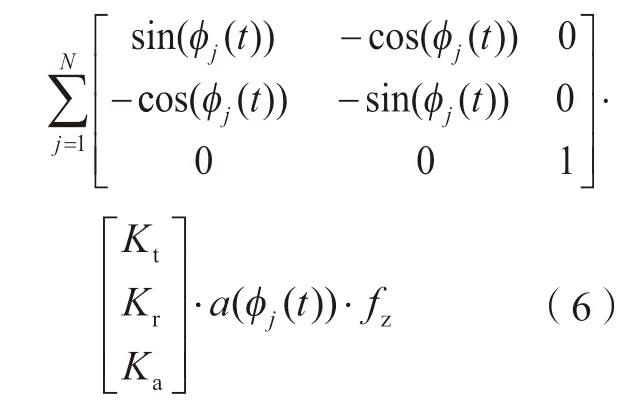
其中，Kt、Kr、Ka通过变进给切削试验进行系数标定。

频域法颤振稳定性模型

所谓再生颤振，即机床由于切削噪声等因素的影响出现微量振动，并在前后两个刀齿切入同一位置时留下不同的波纹，从而产生的相位差，如图4 所示。两个波纹之间的相位差，在接近但不等于加工系统主结构模态的颤振频率处，加工系统的最大切屑厚度将呈指数增长，进而切削力也会呈指数增长，这可能会损坏刀具并产生带波纹的低质量表面。Altintas 等[15–16]提出并验证的铣削和插铣过程中颤振稳定性模型，探究了极限切削宽度与主轴转速的关系，被国内外学者广泛采用，具有较高的可靠性和可重复性。

机床再生颤振可分解为直角坐标轴方向X、Y、Z和扭矩方向θ的再生振动，均影响着瞬时切屑厚度。插铣刀的第j个刀齿在t时刻的瞬时切屑厚度可表示为：

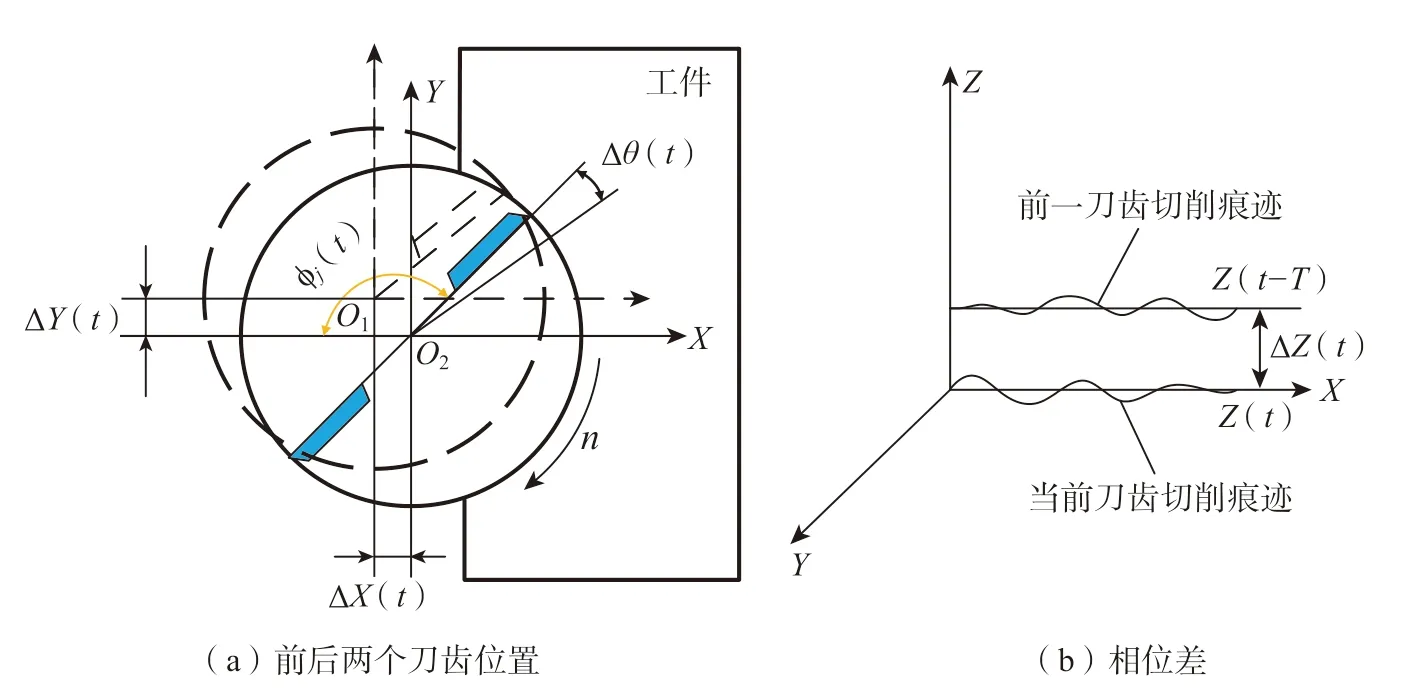
图4 再生颤振示意图Fig.4 Schematic diagram of regenerative chatter

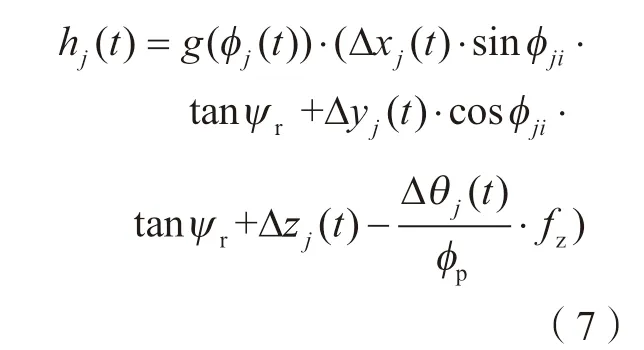
其中，函数g（φj（t））是单位阶跃函数，φst≤φj（t）≤φex时，g（φj（t）） =1；φ（jt）<φst或φ（jt）>φex时，g（fj（t）） =0。此时，瞬时切削力（Ft、Fr、Fa）和扭矩Tθ可表示为：

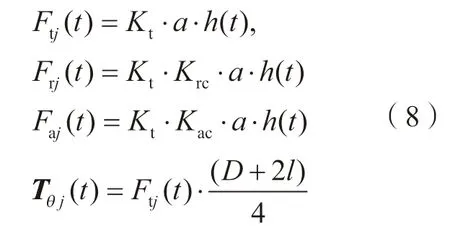
其中，Kr=KtKrc，Ka=KtKac，Krc为径向切向切削力比例，Kac为轴向切向切削力比例，将瞬时切削力和扭矩在笛卡尔直角坐标系下进行坐标变换，并对所有的刀齿进行求和，可得到刀具瞬时总切削力和扭矩为：

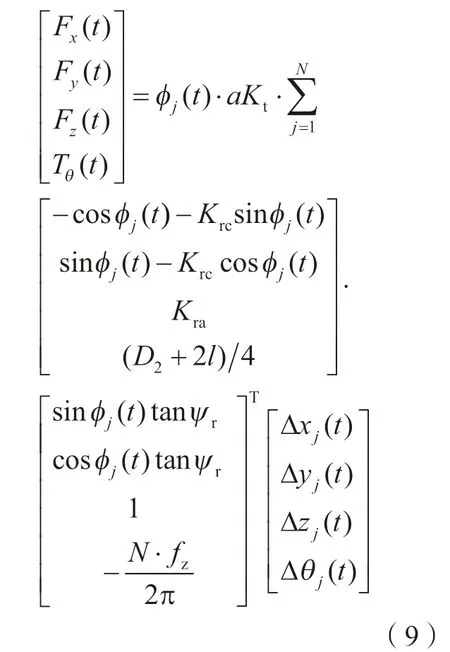
其中，Ψr表示刀具前倾角。

式（9）在时域以矩阵的符号可简化为：

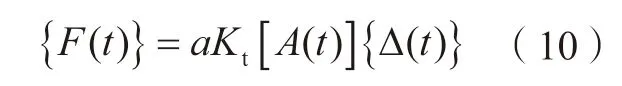
其中，[A（t）]为定向动态切削系数矩 阵。Altintas 等[16]提出，[A（t）]在一个刀齿周期的平均值可作为其近似值，如下：

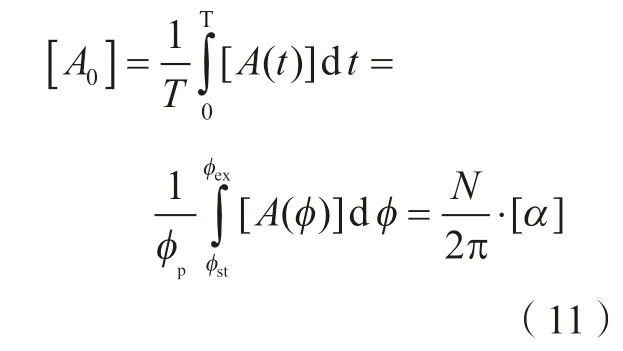
刀具–工件接触区的传递函数矩阵可表示为：

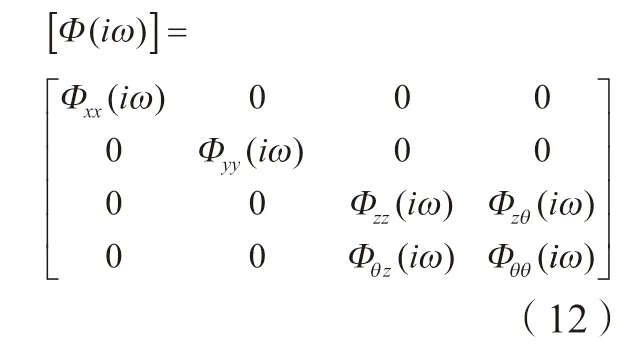
其中，直接传递函数（Φxx（iω）、Φyy（iω）、Φzz（iω）、Φθθ（iω））和交叉传递函数（Φθz（iω）、Φzθ（iω）） 可由下式求出：

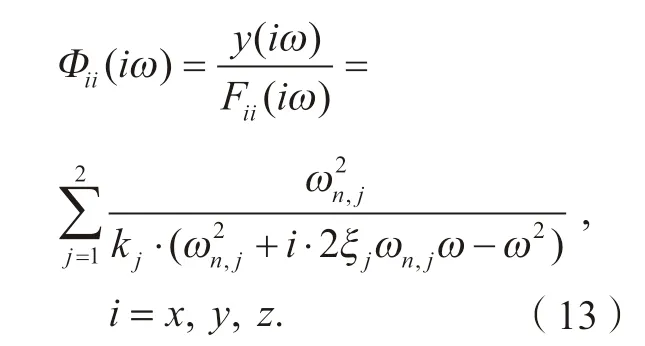
其中，ωn，j、kj、ξj分别是j阶的固有频率、模态刚度和阻尼比，由模态试验测得。

当前时刻t和前一个刀齿周期时刻（t–T）的振动矢量为：

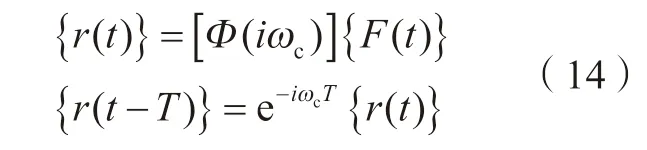
其中，{r（t）}=[x（t）y（t）z（t）θ（t）]T，ωc为谐振频率。因此，再生振动矢量可表示为：

将再生振动矢量方程（15）代入瞬时切削力和扭矩矩阵表达式（9）中，建立插铣稳定性特征值方程：

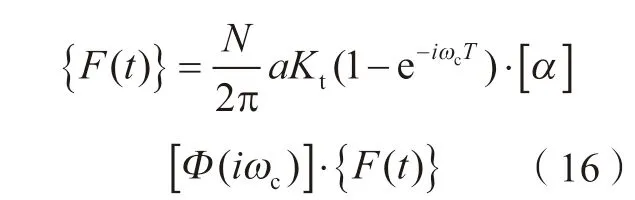
其中，定义定向频率传递函数矩阵Φ0和特征方程的特征值Λ，表示如下：

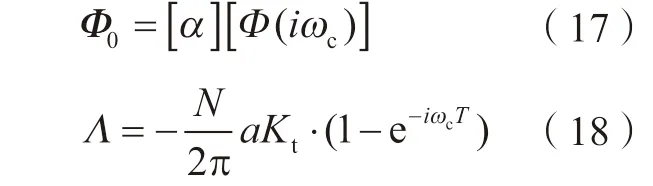
令其行列式为0，其特解为：

由于定向传递函数矩阵Φ0是四阶的，特征方程求特征值可转化为四次多项式的求根问题，如下：

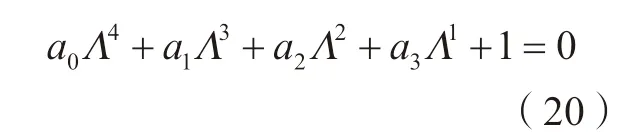
其中，特征值是复数，即Λ=ΛR+iΛI。

Altintas 等[15]指出了临界切削宽度alim与主轴转速n的稳定性叶瓣图的求解方法。临界切削宽度可表示为：

主轴转速n可由刀齿周期T表示为：

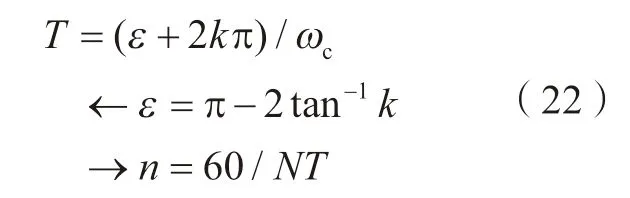
工艺参数多目标优化模型

实际生产加工中，材料去除率与生产成本、加工时间息息相关，因此，提高材料去除率一直是企业追求的目标。当机床、刀具、工件材料选定后，插铣的材料去除率的主要影响因素为主轴转速、每齿进给量、径向切削宽度和侧向步距。槽铣加工的材料去除率可表示为：

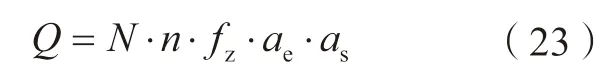
其中，N为刀具齿数，z；n为主轴转速，r/min；fz为每齿进给量，mm/z；ae为轴向切削宽度，mm；as为步距，mm。其中，ae=D。

槽铣加工中，残余高度的控制也非常重要，步距越大，残余高度越大。插铣粗加工时，残余高度的大小决定着精加工的过程，残余高度越小，后续精加工次数更少且精加工过程受力变形更小；插铣精加工时，残余高度的大小体现着表面加工质量，残余高度越大，表面加工质量越差，但材料去除率越高。因此，插铣开槽粗加工工艺中，合理选择步距不仅能够简化后续精加工工艺，也能有效地提高生产效率。残余高度h与步距as的关系可表示为：

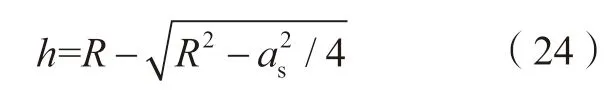
因此，优化目标选定为最大材料去除率和最小残余高度。目标函数的建立一般采用加权法，即fx=ω1·Q（n，fz，as） –ω2·h（as），并使fx最大。但由于材料去除率和残余高度数量级相差太大，在求解过程中优化结果会倾向于数量级较大的材料去除率，残余高度的优化效果并不理想。因此，本研究引入比值加权法，平衡两个优化目标的数量级，其目标函数可表示为：

其中，Qe为材料去除率的期望值；he为残余高度的期望值；ω1、ω2分别为加工效率的权重和残余高度的权重。权重的选择应根据生产需求或数据统计来设定，本研究取ω1=0.5，ω2=0.5。

综上所述，槽铣加工工艺参数多目标优化可表述为：根据槽铣切削力模型和颤振稳定性模型，在切削力约束、稳定性约束、切削参数约束下，找到一组参数，包括步距、每齿进给量和主轴转速，使材料去除率最大和残余高度最小，其数学模型如下：

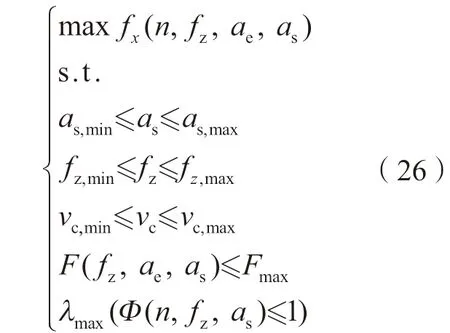
其中，as,min≤as≤as,max为步距约束；as,min为最小步距边界；as,max为最大步距边界；fz,min≤fz≤fz,max为每齿进给量约束；fz,min为最小每齿进给量边界；fz,max为最大每齿进给量边界；vc,min≤vc≤vc,max为切削速度约束；vc,min为最小切削速度边界；vc,max为最大齿切削速度边界，且n=1000vc/πD；F（fz，ae，as）≤Fmax为切削力约束；Fmax为机床稳定工作能负载的最大切削力；λmax（Φ（n，fz，as）≤1）为稳定性约束，可得到每个fz下切削步距as–主轴转速n的稳定性叶瓣图。

试验及优化结果

深槽插铣在航空发动机整体叶环粗加工中有着重要的应用，可以大幅提升叶环的加工效率。通过变进给切削试验标定切削力系数Kt、Kr、Ka，以及锤击试验获取模态参数。进一步利用切削力系数和模态参数计算得到的切削力约束和稳定性约束以及选取切削参数约束边界，代入到工艺参数多目标优化模型中进行求解，最后对比经验参数和优化参数的性能指标。

1 切削试验及锤击试验

选用MIKRON DURO UCP 800 五轴联动机床，刀具为山特维克插铣刀片（R210–025A32–09M）和刀杆（392.410CGA–63 32 09），工件材料为镍基高温合金Inconel718。切削力试验时，如图5 所示，工件安装在Kistler9257B 三向测力仪上，测力仪采集的信号通过信号放大器后传送到NI，并由Labview 软件显示实时切削力信号。变进给量切削力标定试验采用小切宽插铣加工方式，各切削参数设置为：主轴转速n= 620r/min，切削宽度ae= 5mm，侧向步距as= 4mm，每齿进给量fz= （0.03、0.05、0.07、0.09、0.11） mm/z。锤击试验（图6）时，刀具安装在机床主轴上，通过力锤分别敲打刀齿的X、Y、Z方向，加速度传感器将采集的信号传送给模态分析软件，得到X、Y、Z方向的频响函数。θ方向的频响函数由加速度传感器安装在一个刀齿径向平面上，用力锤敲击另一个刀齿径向平面获得；Zθ耦合频响函数由加速度传感器安装在一个刀齿的底部，用力锤敲击另一个刀齿的径向平面获得。

图5 切削力系数标定试验Fig.5 Cutting force coefficient calibration experiment

图6 模态试验Fig.6 Modal experiment

切削力系数标定采用Zhuang[11]提出的小切宽插铣的切削力仿真模型。根据切削参数进行切削力系数标定的结果， 切向力系数Kt为1069.3 N/mm2，径向力系数Kr为1027.5N/mm2，轴向力系数Ka为304.05N/mm2。

将切削力系数代入切削力模型，计算各个切削参数条件的仿真切削力，并与试验切削力值进行对比，其误差均在15%之内，验证了切削力系数的可靠性。选定表1 中的第4组参数，对应一个刀具周期内仿真切削力和试验切削力的变化曲线吻合较好，如图7 所示。

图7 试验与仿真切削力变化曲线Fig.7 Experiment and simulation cutting force curve

通过锤击试验测得的频响函数，再进行模态分析得到机床模态参数，如表1 所示。将模态参数代入到颤振稳定性模型中，可画出临界切削宽度alim与主轴转速n的关系曲线，即稳定性叶瓣图，如图8 所示。

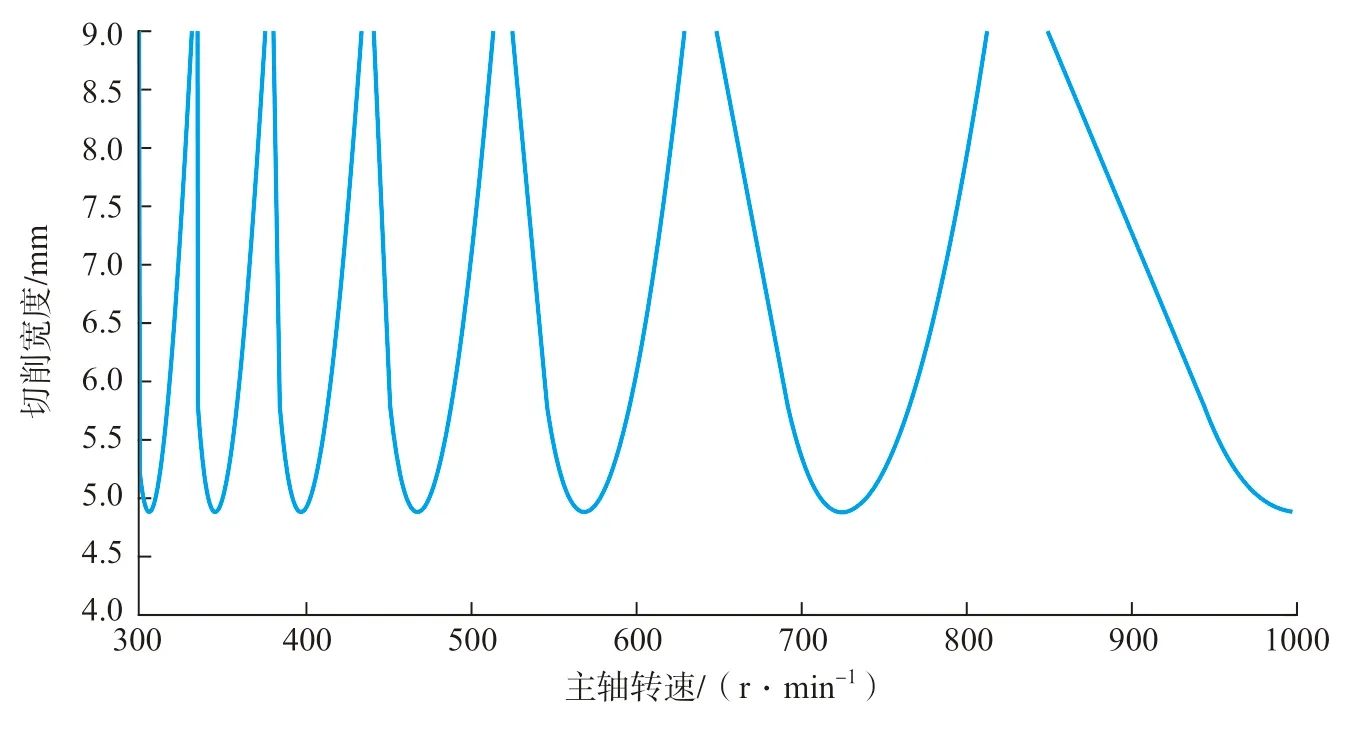
图8 槽铣加工稳定性叶瓣图Fig.8 Stability lobe of slot milling

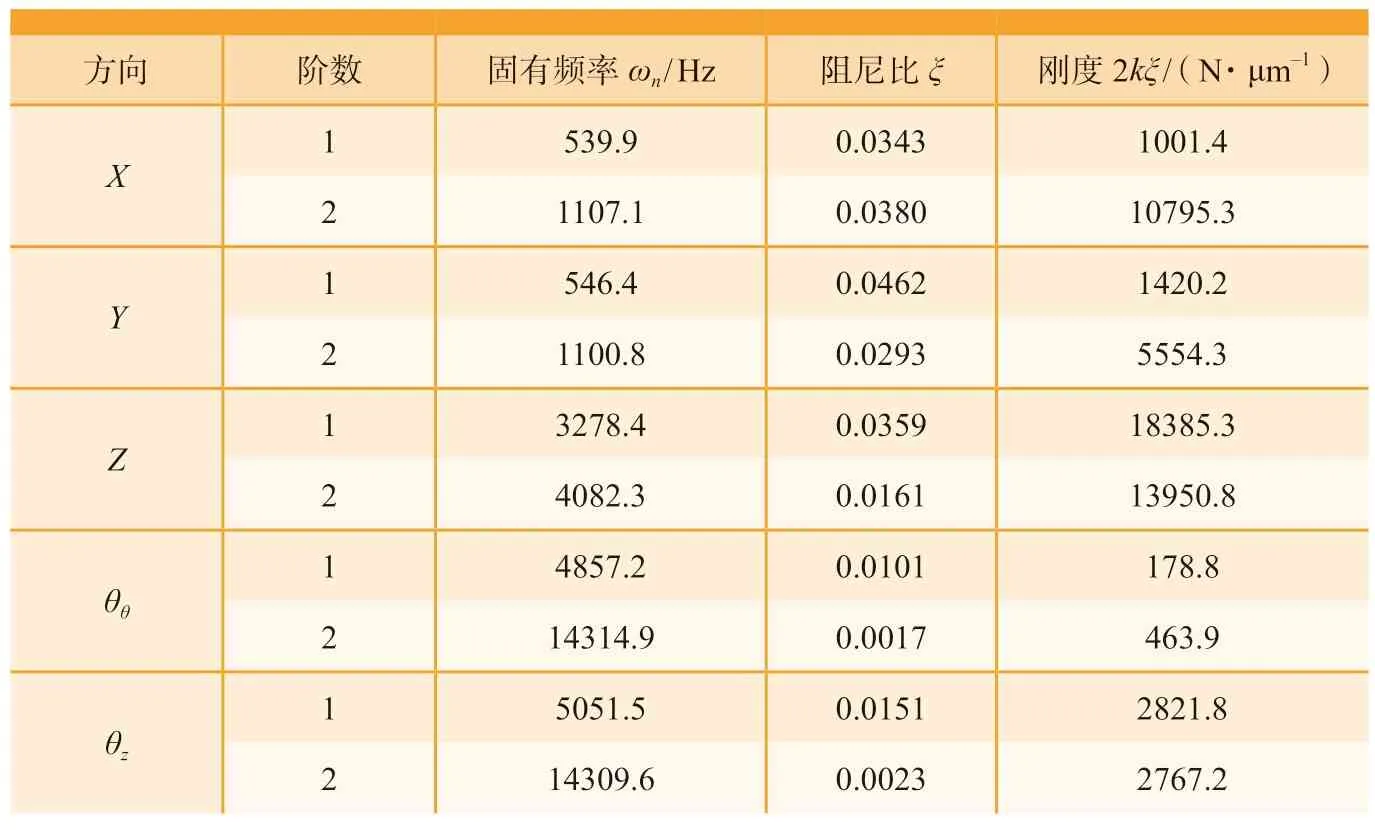
表1 插铣加工系统模态参数Table 1 Modal parameters of plunge milling system

2 切削参数优化实例

由刀具型号可知，刀具参数为：N=2，D=32mm，R=D/2=16mm，L=9mm，Ψr=10°。根据工艺参数多目标优化模型，各个约束条件的边界可选取为：as,min=1mm，as,max=9mm，fz,min=0.03 mm/z，fz,max=0.15mm/z，vc,min=30m/min，vc,max=100m/min，Fmax=1000N。因此，Qe=N·fz,max·ae·as,max=69120mm3/min ，参考机床和刀具加工手册，经验参数为：as=7mm，fz=0.05mm/z，n=620r/min 。

工艺参数优化模型中，目标函数是非线性函数，传统的优化算法搜索范围小、可靠性低，而遗传算法搜索范围广、自适应性好，寻找全局最优解的能力好。因此，本研究采用遗传算法求解多目标优化模型，从而得到最优参数组合。遗传算法的参数设置分别为种群大小500，迭代次数500，突变概率0.3，交叉概率0.8。

求解多目标优化模型实例，对比优化参数与经验参数的性能指标，如表2 所示，优化后参数为：as=5.4 mm，fz=0.119mm/z，n=950.3r/min。 经 验参数下的插铣材料去除率为13888 mm3/min,而优化参数的材料去除率为39487mm3/min，比优化前提高了184.3%；经验参数下的残余高度为0.39mm，优化参数的残余高度为0.23mm，比优化前减小了41.0%。由此可知，优化后参数能提高加工效率且减小残余高度，从而节约加工时间成本，提高生产率。

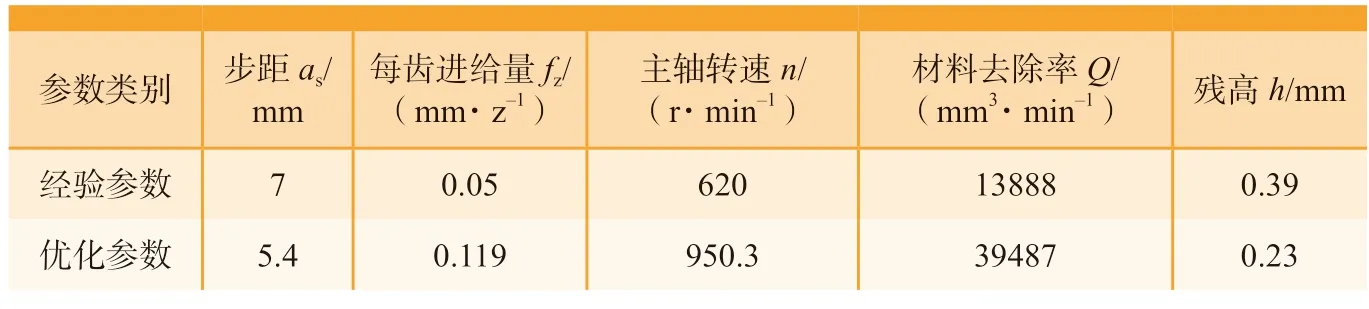
表2 优化参数与经验参数性能指标对比Table2 Comparison of performance indicators between optimized parameters and empirical parameters

结论

（1）在切削力约束和稳定性约束条件下，以最小残余高度和最大材料去除率为优化目标，提出用比值加权法替代加权法，解决了各个优化目标权重难以调节的问题，保证了优化方向的平衡性。

（2）选用优化实例，对插铣刀槽铣的步距、主轴转速、每齿进给量3个切削参数进行优化。相比于经验参数，优化后的材料去除率提高了184.3%，残余高度减小了41.0%。结果表明，优化参数简化了后续加工工艺流程，提高加工效率，在实际生产加工中有重要的指导意义。

（3）磨损和失效的情况，需要开展大量试验来进行研究，由于本研究的篇幅有限，无法将所有的影响因素考虑进来，后续将在本文基础上进一步深入研究。