一种融合专家知识和监测数据的水质预测模型

韩晓霞，陈 媛，胡冠宇,3，唐帅文

(1.火箭军工程大学 作战保障学院，陕西 西安 710025；2.火箭军工程大学 导弹工程学院，陕西 西安 710025；3.桂林电子科技大学 计算机科学与信息安全学院，广西 桂林 541004)

目前，国内淡水存储量局部下降，以废水乱排、水质营养化等形式导致的水质污染在不断加剧[1-2]。我国虽然投入了大量资金进行污水治理，但水污染问题依旧严峻。因此，为尽早发现水污染情况并采取防治方案，水质预测变得十分必要。水质预测主要根据历史数据对未来水质状态进行估计，并为水环境质量、污染物排放等标准的制定提供科学的依据。现有水质预测模型主要分为机理性方法和非机理性方法[3]。例如，WASP(The water quality analysis simulation program)模型[4]以及丹麦学者Liang等[5]研发的MIKE模型可根据各污染物的迁移和转化规律建立水质预测模型，能广泛用于多种不同水环境中[6]。李如忠等[7]运用未确知数学理论建立了未确知数学模型，在监测信息不确定情况下可获得较为准确的水质模拟预测值。文献[8-10]分别提出了基于灰色模型、BP(Back propagation)神经网络以及GM(1,1)灰色动态模型的水质预测方法，借助历史数据建立较为准确的水质预测模型，能够有效适用于洪湖、人工湖等水域的水质预警预报系统中。上述方法在实际应用中均取得较好效果，然而作为一个典型的复杂系统，水环境中污染物对水质的影响不一，且污染物之间存在非线性关系[11]。因此，水环境的未来水质变化趋势预测存在众多不确定性因素，包括随机、模糊不确定性以及无知性[7,12]。同时，由于受监测技术限制，获取的历史水质监测数据较少。单纯利用传统的机理性或非机理性方法进行水质预测已不再满足精度要求。置信规则库(Belief rule base, BRB)[13]模型作为机理与非机理性方法的折中，能够充分利用专家知识与历史监测数据实现对水质的预测，可有效缓解监测数据较少问题。同时，该模型也能处理包括随机、模糊不确定性等多种不确定性，并利用辨识框架(Frame of discernment, FoD)(由单个集合和系统状态构成的通用集合)很好地表达带有无知性的信息。无知性可以进一步分为全局无知性(根据现有知识无法确定最终结论)和局部无知性(根据现有知识可以确定结论存在于某个子集中)。BRB中辨识框架FoD只能描述全局无知性问题。以水环境为例，假设水质健康状况有3 个评估等级，BRB模型的辨识框架表示为FoDBRB={{good},{common},{bad},{good,common,bad}}。环保部门采取一系列措施将富营养化状态的湖泊治理并恢复到正常状态。因此，湖泊在短时间内具有很强的自愈能力，{bad}状态可以排除在湖泊水质预测结果之外，这意味着大部分的置信度应该分配给{good, common}的子集。但如果无知性被分配给{good, common,bad}全集，将会导致置信度分布不合理，建模精度下降。幂集[14]是指由单一集合及其所有子集组成的集合，具有完备的局部和全局无知性知识的描述能力，能较好地解决水质预测问题中存在的局部无知性问题。

笔者提出一种幂集置信规则库(Belief rule base with power set, PBRB)的水质预测模型。首先，将FoD拓展至幂集来描述水质预测中存在的局部无知性，利用证据推理(Evidential reasoning, ER)算法[15]将影响对水质关键指标的融合评价，将评估结果输入到水质预测模型中得到下一时刻的水质健康状况预测值；其次，利用协方差矩阵自适应进化策略(Covariance matrix adaptive evolution strategy，CMA-ES)[16]算法对PBRB模型进行优化，避免水质预测模型初始参数设置不准确，进一步提高水质预测的精度；最后，以海口市东寨港贝类养殖区为例对所构建的模型进行验证。

1 基本原理

1.1 置信规则库预测模型

为有效地处理模糊、不完全和非线性因果关系，Yang等[13]基于传统IF-THEN规则的知识库结构，将置信度嵌入到规则库中，建立BRB模型。置信结构使BRB能够更灵活地表示含有不确定性的知识。目前已被广泛应用于故障预测、网络安全态势和系统行为预测等领域[14,17-18]。例如，Zhou等[19]提出了通过一种隐含置信规则库预测模型来预测陀螺漂移系数；Zhou等[20]在BRB模型的基础上，建立了WD615型柴油机隐性故障预测模型。

本节将回顾BRB预测模型的主要内容，为笔者提出的新预测模型提供依据。首先，假设Θ表示一个由N个状态或命题构成的集合，且Θ={T1,T2,…,TN}。BRB预测模型辨识框架选用FoDBRB={∅,{T1},{T2}…,{TN},Θ}，Θ表示全集，∅表示空集。作为一种非线性系统建模工具，BRB预测模型主要是建立置信规则库来表示当前时间和未来时间系统行为之间的关系。其中，第k条规则可以表示[21]为

如果x(t)处于状态Tk时,且θk=δ=1,则x(t+1)的状态为

{(T1,β1,k),(T2,β2,k),…,(TN,βN,k)}

(1)

其中：x(t)为系统在t时刻的行为；Tk为第k个结论等级；βj,k(j,k=1,2,…,N)为第k条规则中第j个结论等级的置信度，N为规则总数，值得注意的是，BRB预测模型中的规则数与结论等级个数相等；θk为第k条规则的规则权重，在BRB预测模型中，由于前提属性只有一个，所以属性权重设置为1，即δ=1。

在水质预测问题中全局与局部无知可能同时存在，无论忽略哪种无知性，模型都可能错误反映客观事实。因此，将FoD拓展到幂集并将置信度分配给全集和其子集，能够更好地表示全局与局部无知性。

1.2 一种新的基于置信规则库预测模型

在BRB预测模型基础上，建立PBRB预测模型。首先，将FoDBRB扩展到幂集，记作FoDPBRB={∅,{T1},{T2},…,{TN},{T1,T2},{T1,T3},…,Θ}。FoDPBRB被认为是一个统一的框架，其中置信度不会分配给空集，而是分配给剩余其他子集。PBRB预测模型中的第k条规则可以改写成

如果x(t)处于状态Tk,且θk=δ=1,则x(t+1)的状态为

{(T1,β1,k),(T2,β2,k),…,(TN,βN,k),
(TN+1,βN+1,k),…,(T2N,β2N,k)}

(2)

其中：x(t)为系统在t时刻的行为并描述在幂集上；Ti(i=1,2,…,2N)为系统的第i个状态(或者是第i个结论)，Ti⊆FoDPBRB；βj,k(j,k=1,2,…,2N-1)为第k条规则中第j个结论的置信度。由于置信度不会分配给集合∅，因此PBRB预测模型中的规则总数为2N-1。同样，前提属性只有一个，所以δ=1。

2 基于幂集置信规则库的水质预测模型

2.1 基于证据推理算法的水质评估

为实现对水质健康状况的预测，需要先对水质进行评估。考虑到ER算法在处理各类不确定性方面的优势[22-23]，利用该算法融合多个影响水质的关键指标，实现水质健康状况评估。水质健康状况评估的流程如图1所示。

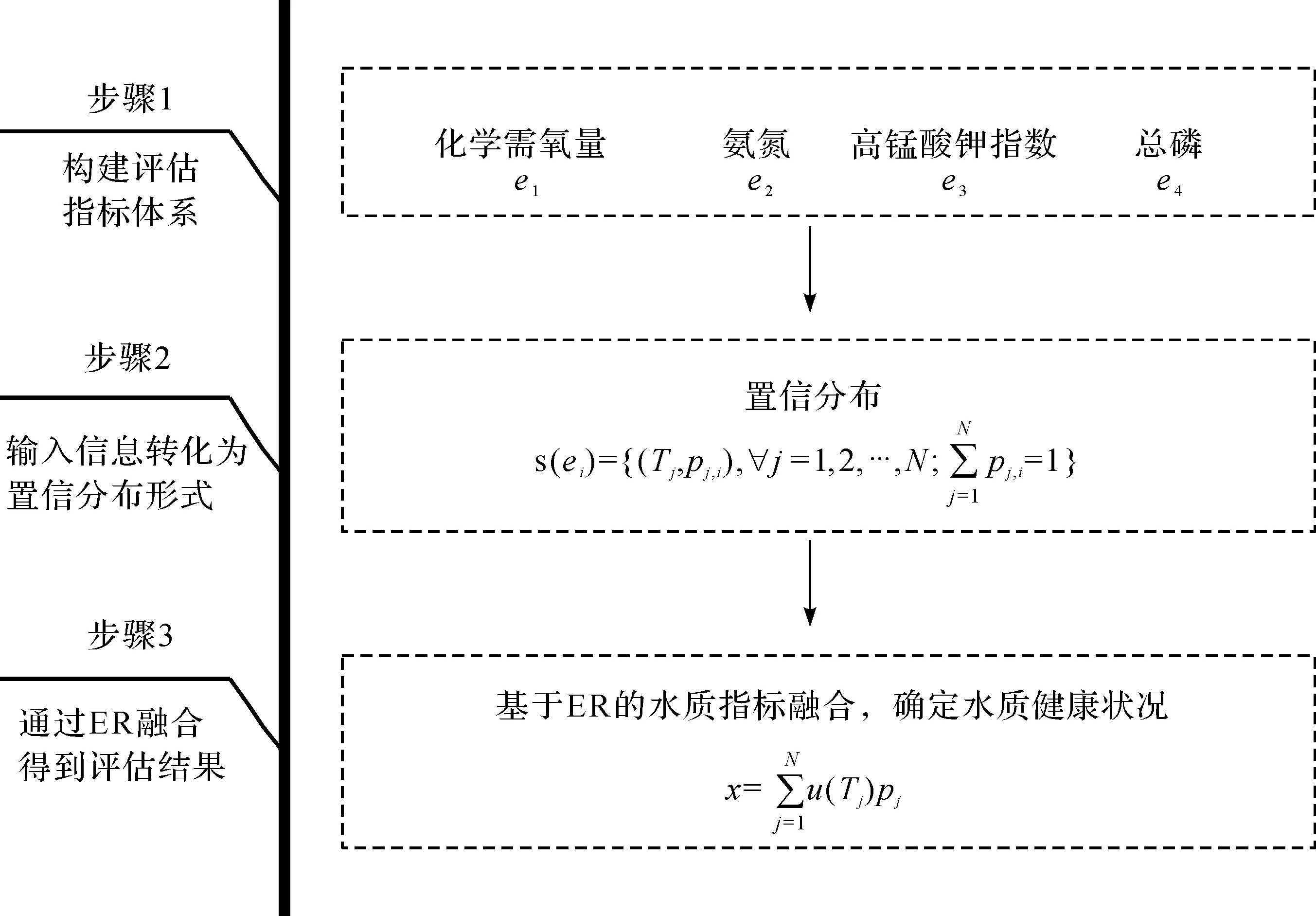
图1 水质评估流程Fig.1 Water quality assessment process

具体水质评估流程如下：

步骤1构建评估指标体系。由《地表水环境质量标准》可知：多个水质监测指标会直接影响水环境质量等级。若水质指标过多，模型计算量增大。因此，选取化学需氧量、氨氮、总磷和高锰酸钾指数含量这4 个指标作为水质评估的关键因素[24-25]，如图1所示。

步骤2水质监测信息转换。在4 个水质监测指标进行融合前，将水质监测数据转化为置信分布形式。每个评估指标表示一条证据ei，其对应的置信分布为

(3)

式中：Tj表示第j个评估结论等级；pj,i表示证据ei相对于结论等级Tj的置信度，其中pj,i可以采用基于效用的方法[26]计算，也可以由专家给定。

步骤3多个水质指标融合，得到水质健康状况。将4 个指标进行融合，可得到水质的健康状况x为

(4)

式中：x为融合输出结果，表征当前水质的健康状况；u(Tj)为第j个结论等级Tj对应的语义值；pj为融合后所得结果支持结论等级Tj的置信度，可通过计算得到[27]，即

(5)

(6)

mj,I(i+1)=KI(i+1)[mj,I(i)mj,i+1+mj,I(i)mT,i+1+
mT,I(i)mj,i+1]

(7)

(8)

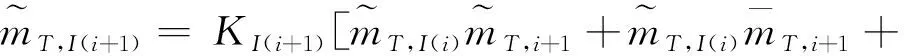
(9)

mj,i=wjpj,i

(10)

(11)

(12)

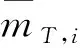
2.2 PBRB水质预测模型的建立

在得到水质健康状况后，还需要建立PBRB水质预测模型的置信规则库，以表征当前时刻与下一时刻水质健康状况之间的非线性因果关系。

步骤1置信规则库的框架确定。根据2.1节给定的水质健康状况评估等级，计算得到模型的规则数L=2N-1，可确定置信规则库的框架。

步骤2置信规则库初始参数的确定。根据专家知识以及相关标准，确定初始参数Ω={θ1,θ2，…,θ2N,β1,1,β2,1,…,β2N,1,β1,2,β2,2,…,β2N,2,…,β1,2N-1,…,β2N,2N-1}以及辨识框架FoDPRBR。

步骤3水质预测模型的构建。在上述步骤的基础上，构建了初始置信规则库，即完成了初始PBRB水质预测模型的建立。其中模型的第k条规则可以表示为

如果x(t-1)处于状态Tk,且θk=δ=1,则x(t)的状态为

{(T1,β1,k),(T2,β2,k),…,(TN,βN,k),
(TN+1,βN+1,k),…,(T2N,β2N,k)}

(13)

式中：x(t-1)为在t-1时刻水质健康状况；x(t)为预测得到的第t时刻的水质健康状况；Tj(i=1,2,…,2N)为第j个水质健康状况等级，Ti⊆FoDPBRB；βj,k(j,k=1,2,…,2N-1)为第k条规则中属于第j个水质健康状况等级的置信度。

2.3 PBRB水质预测模型的推理

基于上述分析，得到水质健康状况并完成了PBRB水质预测模型的建立。因此如何利用PBRB水质预测模型预测未来水质健康状况成为本小节的研究重点，基于PBRB的水质预测模型推理为

步骤1计算输入的匹配度。其中，PBRB水质预测模型的输入数据可以是定性或定量数据。在本研究中，由于PBRB水质模型的输入是评估得到的水质健康状况，即为定量数据。因此，可以计算得到输入相对于参考值的匹配度，即

(14)

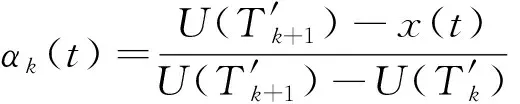
(15)

式中：U(Ti)为幂集评价等级下第i个命题的效用；U(T′j)为单集评价等级下第j个命题T′j(j=1,2,…,N)的效用；α′i(t)和αj(t)分别为输入x(t)相对于幂集评价等级与单集评价等级效用的匹配程度。

步骤2当t-1时刻的输入为x(t-1)，计算出t时刻的条件概率密度p(x(t)=U(Tj)|x(t-1))，即

(16)

式中βj(t)为在时刻t分配给第j个结论的置信度，具体计算公式为

(17)

(18)

式中：wk(t)为在时刻t分配给第k条规则的激活权重；βi,k(t)为在时刻t分配给第k条规则中第i个结论的置信度，初始值可由专家根据经验给定，并结合优化算法进一步优化。

由于所求的概率分布是分配给幂集的，依旧存在不确定状态，因此需要将其重新分配给单集，得到t时刻的水质健康状况预测值为

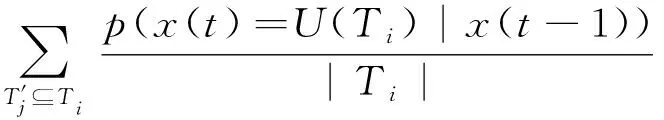
(19)

(20)

式中|Ti|为集合Ti中包含的元素个数。

2.4 基于CMA-ES的水质预测模型参数优化

由于专家知识的无知性，导致初始PBRB水质预测模型中的参数设置不准确。因此，很有必要对预测模型的参数进行优化，以提高预测精度。确定优化目标，即

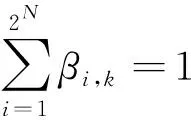
(21)

式中H(Ω)为实际输出与估计输出之间的均方误差函数。待优化的参数向量可以表示为Ω={θ1,θ2,…,θ2N,β1,1,β2,1…,β2N,1,β1,2,β2,2,…,β2N,2,…,β1,2N-1,β2,2N-1,…,β2N,2N-1}。

由于CMA-ES算法能够在相对合理的时间内利用少量种群收敛至全局最优，且在处理高维非线性优化问题上性能良好[16]。因此，笔者利用CMA-ES优化算法通过初始化、选择重组和更新操作等步骤，求解上述优化问题，具体步骤参考文献[16]。

2.5 水质预测模型建模步骤

基于上述分析，PBRB水质预测模型建模流程的基本步骤如下：

步骤1融合影响水质关键指标，得到水质健康状况。利用ER算法将化学需氧量、氨氮等水质监测关键指标融合评价，并将得到的水质健康状况作为预测模型的输入。

步骤2建立置信规则库。结合专家知识和行业标准，确定模型规则总数、初始化模型参数Ω以及辨识框架FoD，构建置信规则库，从而建立初始PBRB水质预测模型。

步骤3利用CMA-ES算法进行参数优化。借助CMA-ES优化算法，可以获得目标函数为最小时所对应的最优参数，并得到最佳水质预测模型。

步骤4推理得到预测结果。将所得到的水质健康状况输入到水质预测模型中，利用式(14～19)，可计算基于幂集评价等级的水质健康状况预测结果。

步骤5利用式(19)将式(16)得到的幂集评价等级下的结论置信度重新分配给单集评价等级，得出最终的水质健康状况预测结果x(t)。

3 算例实现

3.1 PBRB水质预测模型的建立

下面给出海口市东寨港贝类养殖区24 个月的历史水质监测数据，如图2所示。参考《地表水环境质量标准》(GB 3838—2002)可知：确定该水域属于III类水质并给出各水质监测指标所对应的参考等级和参考值。同时，将水质健康状况分为好(G)、中(M)和坏(S)3 个评估等级，如表1，2所示。其中，水质健康状况数值越大表示水质越干净。

图2 某渔业水域不同监测指标24 个月监测数据Fig.2 24 months monitoring data of different monitoring indexes in a fishery water area

表1 水质监测指标参考等级和参考值

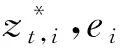
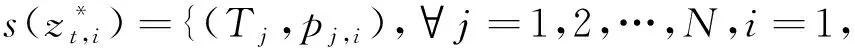
(22)

(23)

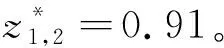
表2 水质健康状况参考等级和参考值Table 2 Reference grade and value of water quality health status

(24)

证据e2可表示为输入置信分布形式，即

s(0.91)={(T1,0),(T2,0.18),(T3,0.82)}

(25)

同理，图2中的所有水质监测指标监测数据可转换为证据的置信分布形式，在此不赘述。采用式(3～12)对4 个水质监测指标进行融合，得到24 个月的水质健康状况，其变化趋势如图3所示。

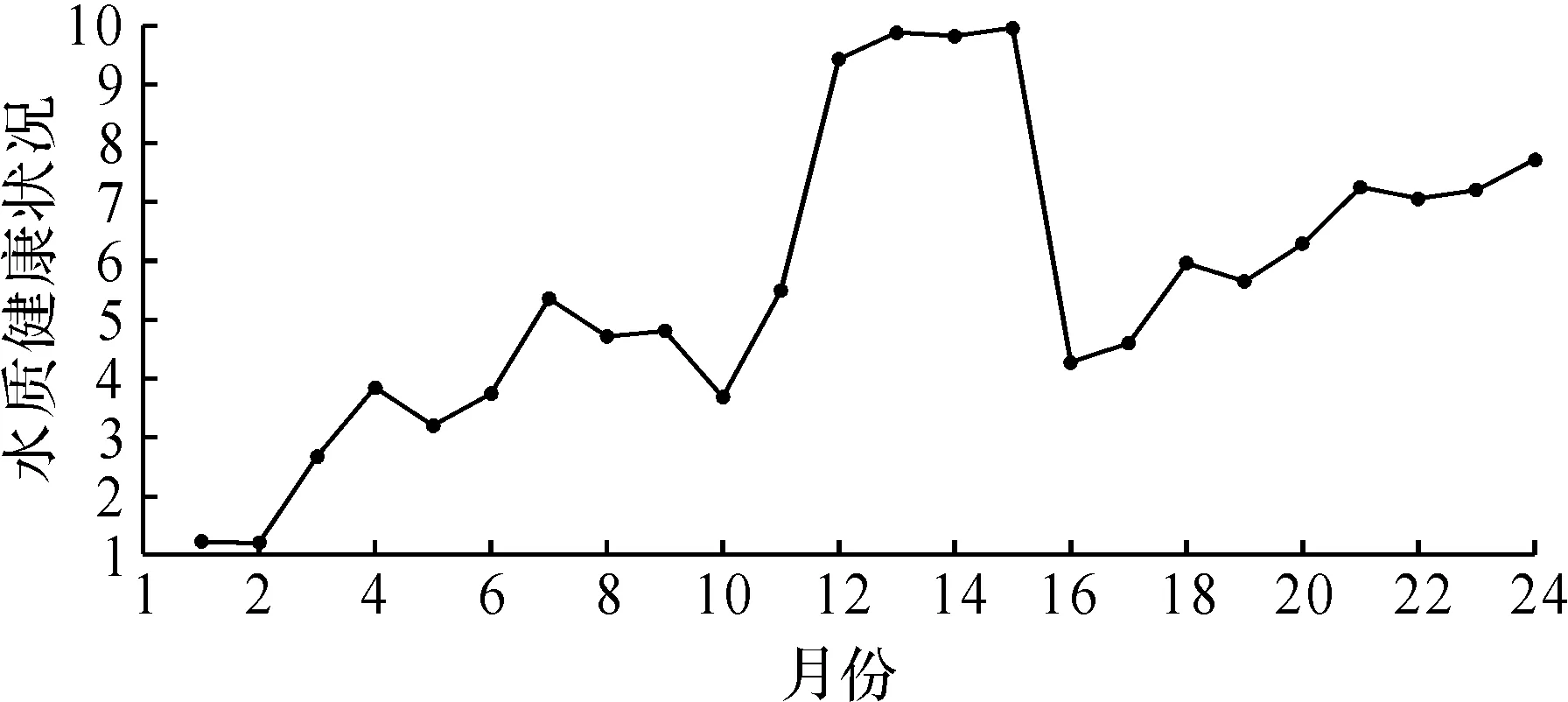
图3 24个月水质健康状况变化趋势图Fig.3 Trend of water quality in 24 months

基于上述分析，可知水质健康状况等级可分为3 类，则PBRB水质预测模型中置信规则库的规则总数为23-1条。结合行业标准以及专家知识，可初始化模型参数Ω={θ1,θ2…,θ7,β1,1,β2,1,…,β8,1,…,β1,2,β2,2,…,β8,2,…,β1,7,β2,7,…,β8,7}以及确定辨识框架FoDPBRB={∅,{G},{M},{S},{G,M},{G,S},{M,S},{G,M,S}}的取值，最后实现初始PBRB水质预测模型的构建，如表3所示。表3中结论置信度由专家给出，并且没有给空集分配置信度。以最后一行为例，置信度都分配给集合{G,M,S}，这意味着专家没有先验知识来预测未来水质状态。

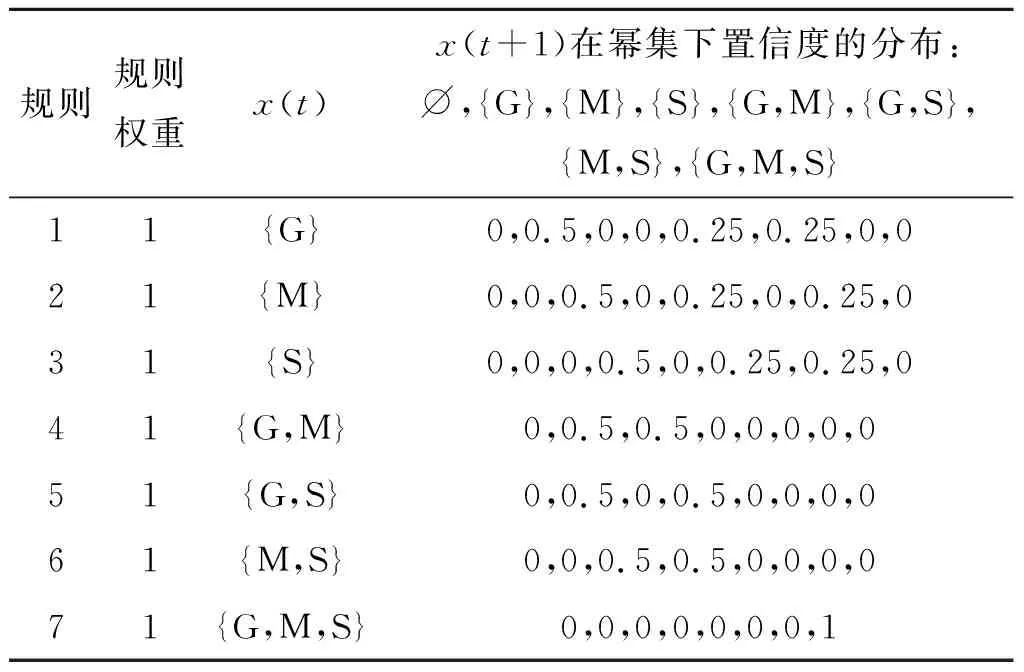
表3 初始PBRB水质预测模型Table 3 Initial water quality prediction model based PBRB

3.2 PBRB水质预测模型的训练

本节选取CMA-ES算法作为优化工具，可计算得到模型的最优参数。将待优化的56 个初始参数作为初始期望，迭代次数设为45。实验将融合得到的24 个月的水质健康状况作为数据集，随机抽取16 个月的水质健康状况作为训练数据，后8 个月作为测试数据对初始模型进行训练，笔者选用均方误差表示模型的预测精度。优化后的结果如图4和表4所示。优化前后的PBRB水质预测模型的预测精度分别是0.95和0.74。图3结果也表明：经过CMA-ES优化后的PBRB水质预测模型能够较好地预测未来水质状况。

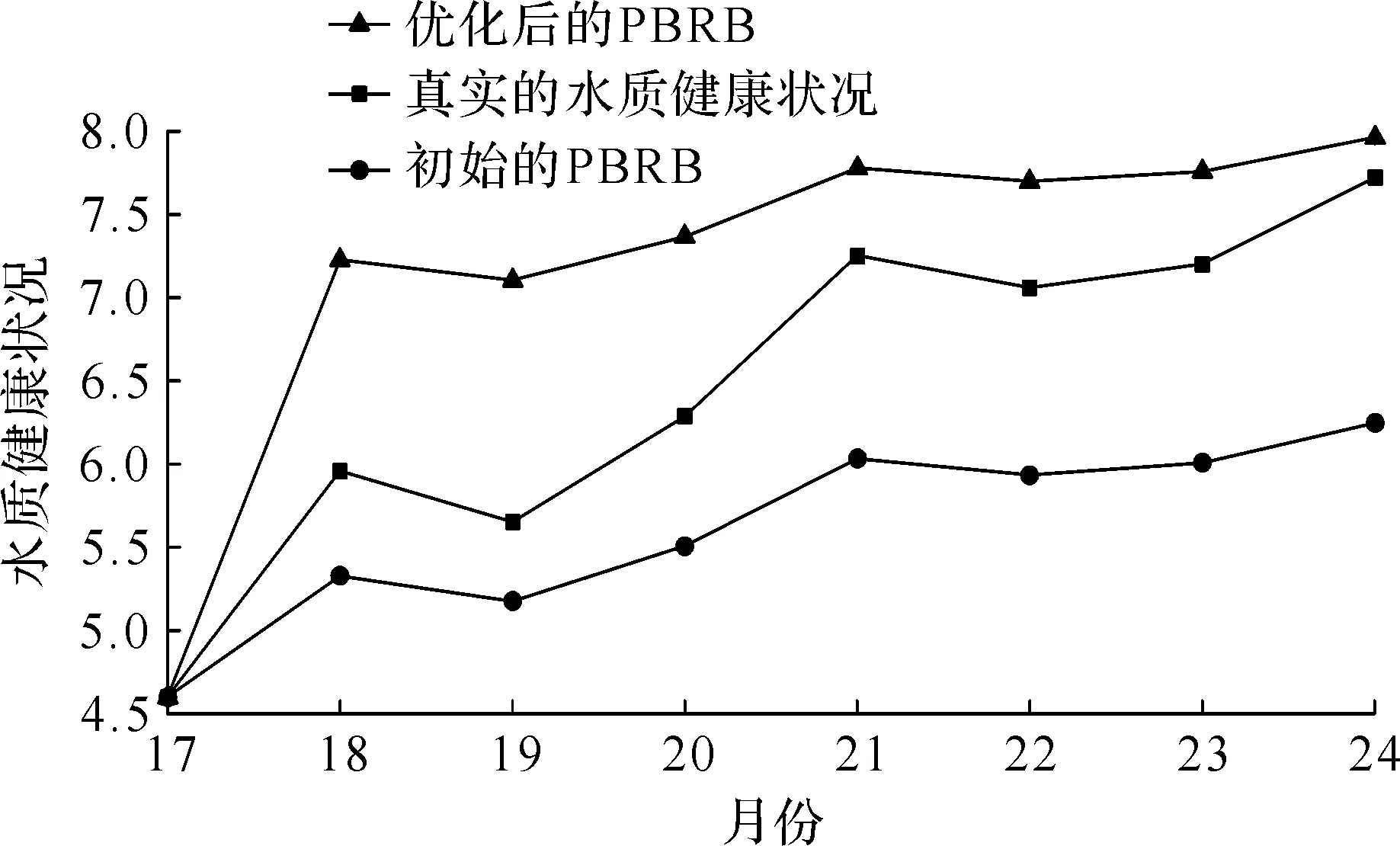
图4 经CMA-ES优化的PBRB水质模型预测结果Fig.4 Prediction results by the optimized PBRB model

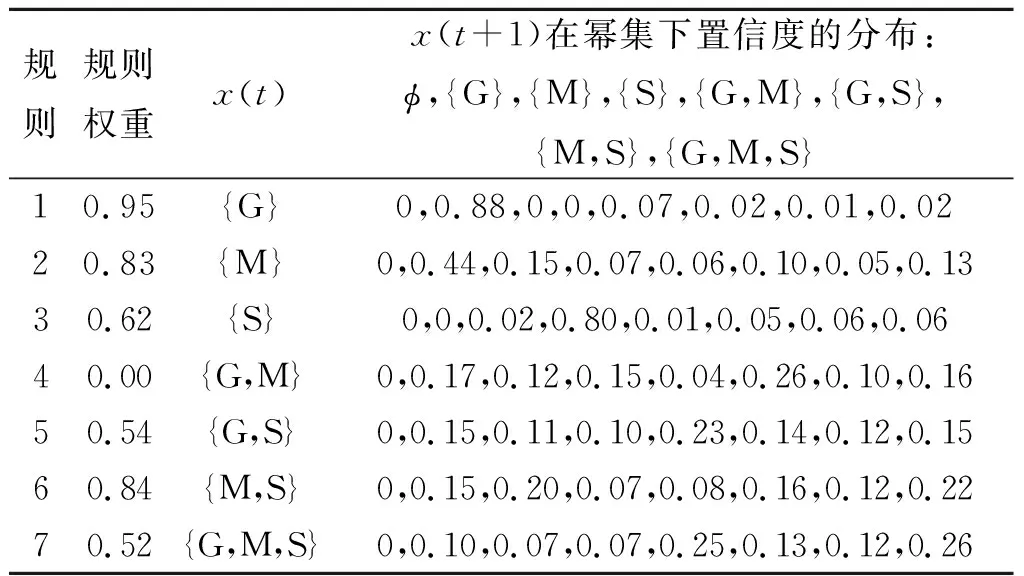
表4 优化后PBRB水质预测模型

3.3 对比实验

为证明所提模型的有效性，将PBRB预测模型与BRB模型、BP模型和自回归移动平均模型(Autoregressive integrated moving average model，ARIMA)[28]预测法进行对比实验。后8 个月的水质健康状况的预测结果以及预测精度如图5和表5所示。

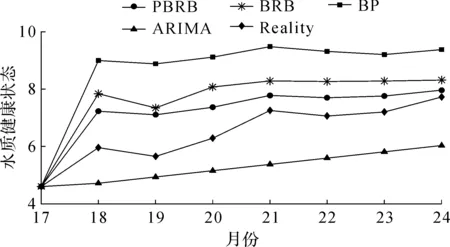
图5 多种预测算法对比结果图Fig.5 Comparison results of various prediction algorithms

表5 各个水质预测模型的预测精度

从4 种方法的预测结果来看，PBRB预测模型的预测精度最高，其次是BRB、ARIMA和BP预测模型。主要原因是PBRB预测模型相比于BRB预测模型可以更为完善地描述知识，能够适应特殊的水环境。由于ARIMA预测模型只考虑了指标随着时间变化规律，无法对复杂水质环境的不确定性进行描述，所以其预测精度最低。而BP预测模型预测的结果与真实水质变化趋势虽然相似，但在历史数据量不大的情况下，预测精度相对不高。因此，笔者所提PBRB预测模型能够很好地描述水质预测问题中存在的局部无知性与全局无知性，更加精准地将置信度分配给相对应的区间，提高了预测精度。

4 结 论

由于水环境的复杂性，水质与污染物之间存在多种无知性及不确定性。笔者提出的基于幂集置信规则库(Belief rule base with power set, PBRB)的水质预测模型可利用专家知识与水质监测数据对水质健康状况进行综合预测，在样本数据较少的情况下突出优势。该模型不仅保留了BRB的优势，而且能够更好地描述水质预测中存在的局部无知性，从而消除了一些不可能的情况。同时，借助CMA-ES优化算法对初始PBRB模型进行优化，可进一步提高水质预测精度。实验结果表明：PBRB模型具有更高的预测精度且有更强的先验知识描述能力，在水质预测领域具有广阔的应用前景。为了进一步提高水质预测的准确性，未来可以考虑监测数据受干扰后造成的不确定性，以实现更全面的水质预测。