基于遗传最小二乘支持向量机的初次给水管漏损时间预测模型

陈 磊，王培永

(1. 浙江工业大学 土木工程学院，浙江 杭州 310023；2.柯桥排水有限公司，浙江 绍兴 312030)

近年来我国城市给水管网系统平均漏损率达到15.3%，部分城市超过25%。控制漏损能够节约大量的水资源，提高供水的安全性和可靠性。科学地预测管道漏损时间，将为系统的维护和更换提供决策支持，能够一定程度减少漏损的发生率，增强系统的安全性。

张宏伟等[1]根据管网漏损的主要影响因素，采用线性回归分析法建立模型，但是该方法难以反映漏损影响因素和漏损时间之间复杂的非线性关系。覃炫[2]和邵圆媛[3]分析了漏损的主要影响原因，分别采用具有较强非线性映射能力的BP网络和改进BP网络来预测管道漏损时间，但是未提出解决网络参数确定和过学习等问题的方法。基于结构风险最小化的LSSVM仅需确定两个参数，并且具有比神经网络更强的预测性能[4-5]。针对传统基于交叉验证的LSSVM建模耗时长的不足，笔者提出了采用全局寻优能力较强的AGA优化LSSVM参数的建模算法，以获得更好的建模速度和预测效果。

1 影响初次管道漏损的主要因素

众多因素将对管道漏损产生影响，比如：管材、施工质量、管道腐蚀、地面荷载、管径、管道埋深和管道压力等，但是考虑太多因素会使模型变得复杂，并且管材、施工质量和管道腐蚀等因素很难量化。因此，主要因素取管顶覆土、管径、管道压力和管道所在道路等级。

2 基于AGA-LSSVM的管道初次漏损时间预测模型

2.1 LSSVM算法

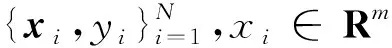
目标函数为

s.t.yi=wTφ(xi)+b+eii=1,…,N

(1)

式中：μ和ζ为参数；w∈Rnf为权值；φ(·):Rm→Rnf为映射函数；b为偏置；ei∈R为误差。

构造计算式，即

(2)

式中αi为乘子。

求偏导，即

(3)

去掉w和e，得到

(4)

式中：y=[y1,y2…,yN]T；1v=[1,1,…,1]T；α=[α1,α2…,αN]T；I为N×N的单位阵；Ωil=φ(xi)Tφ(xl)=K(xi,xl),i,l=1,2…,N。

求出α和b，则LSSVM为

(5)

因此，LSSVM仅需确定参数σ和γ，但传统基于交叉验证的参数优化方法耗时较长。

2.2 AGA优化LSSVM的参数

引入全局寻优能力较强的AGA[6]优化参数，具体过程为

1) 编码。σ，γ的取值范围[7]为[0.01,50]，各取12 位二进制，个体长度为24 位。

2) 选择。采用轮盘赌法选择个体。

3) 自适应交叉和变异。交叉采用两点法。对于每对个体，从(0, 1)范围中随机产生一个数：若该数小于交叉率Pc时，每对个体随机选两个点，交叉互换后获得两个新个体；当该数大于Pc时，则不执行交叉。交叉率为

(6)

式中：f′为两个体适应值中的较大值；favg为每代的平均适应值；fmax为每代的最大适应值。变异采用单点法。对于每个个体，从(0,1)范围内随机产生一个数，若该数小于变异率Pm，则在个体中随机选一位数变异，将1变成0，或者0变成1；否则不变异。变异率为

(7)

式中f为变异个体的适应值。

4) 保留较优个体。父代一半数目的适应值较小个体将由子代适应值较大个体所替代。

2.3 基于AGA-LSSVM模型的建模和预测

某县给水干管一般采用球墨铸铁管和钢管，其中球墨铸铁管漏损数据较齐全，共有数据26 组，因此仅针对球墨铸铁管进行预测。

将前21 组数据等分成3 份，以每个解码后的个体为LSSVM的参数，采用3 折交叉验证计算个体的适应值(即在利用2 份数据训练LSSVM后，预测剩下的1 份数据，选取1 份不同数据进行预测，得到3 次预测结果)，其计算式为

(8)

式中：yij为第i次预测中第j组数据对应的实际漏损时间；Fij为第i次预测中LSSVM对第j组输入数据的预测结果。

建模及预测的过程如下：

1) 采用归一化的方法预处理训练数据、预测的输入数据，并且反预处理预测结果。

2) 最大进化代数Gmax取100，进化代数G取1。随机生成并解码200 个父代个体，得到200 组(σ,γ)，根据式(8)计算各个体的适应值。

3) 若G等于Gmax+1，转到步骤5)；若否，则判断G是否等于1：若是，转到步骤4)，若否，解码，计算个体适应值，并用100 个子代较优个体替代父代较差个体，构成新父代。

4) 对父代执行选择、交叉和变异，得到子代，G=G+1，转步骤3)。

5) 以适应值最大个体对应的参数为LSSVM模型的最优参数，用21 组数据训练该模型，模型对26 组数据中最后5 组输入数据(需归一化)进行预测，反预处理后，得到实际预测值。

为了验证AGA的优化能力，在配置为CPU Intel Core2 Duo E7 400 2.8 G，2 G DDR的笔记本上进行10 次测试，该算法每次都能搜索到如图1所示的最优解，搜索到最优解的最短时间为412 s，最长时间为465 s，平均时间为433 s。最短时间获得最优解的最大适应值和平均适应值的变化曲线分别见图1，2(其他测试的结果与两图类似)，计算得到的最优个体为(11.417，9.404)，基于AGA-LSSVM模型(模型1)的预测结果详见表1。

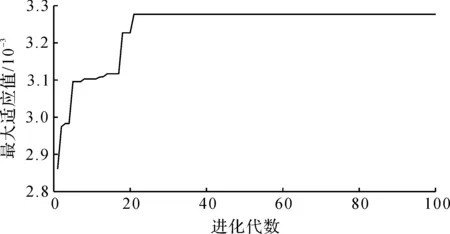
图1 最大适应值变化曲线Fig.1 Curve of maximum fitness values

表1 两模型预测值和实际值的对比Table 1 Comparison of the prediction values and the actual values between two models

由图1可知：AGA具有较强的全局寻优能力，能够在进化中迅速脱离局部最优，搜索到更优个体，同时也具有较快的收敛速度，在第21代已找到最优解。由图2可知：46 代后种群的平均适应值变化很小，表明个体基本不变，种群进化已基本结束。

图2 平均适应值变化曲线Fig.2 Curve of average fitness values

为了进一步验证AGA的优化性能，将其与网格交叉验证法进行对比。交叉验证中，σ和γ的范围也取[0.01, 50]。网格划分方法：先对区间内的σ和γ粗划网格，各取{0.01,0.025,0.05,0.075,0.1,0.25,0.5,0.75,1,1.5,2,2.5,3,…,49,49.5,50}，网格点一共有107×107 个，采用3 折交叉验证计算各点的适应值(数据和计算方法与AGA优化相同)，然后以适应值最大的网格点为中心细分网格，共得到网格点201×201 个，优化后得到最优点为(3.17, 4.32)，耗时875 s。采用相同的21 组数据训练模型后，得到表1所示的基于交叉验证LSSVM模型(模型2)的预测结果。

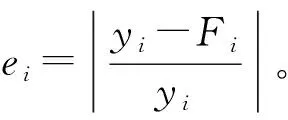
综上，无论是对于优化时间、单个预测结果还是平均预测结果，基于AGA-LSSVM模型都全面优于基于交叉验证LSSVM模型。采用传统的网格交叉验证法优化LSSVM的参数，不仅耗时，而且优化结果很大程度取决于如何划分网格。而采用全局寻优能力较强的AGA优化LSSVM的参数，不仅缩短了建模时间，而且获得更高的预测精度。

3 结 论

笔者利用AGA优化LSSVM参数，建立了基于AGA-LSSVM管道初次漏损时间预测模型。实例分析结果验证AGA具有更强的全局寻优能力，能够迅速找到LSSVM模型的最优参数，显著地提高了建模速度，并且基于最优参数的LSSVM模型通过对训练数据的深入学习，精确掌握了主要影响因素与漏损时间之间的复杂非线性关系，能够对相同管材管道的初次漏损时间进行高精度预测。