基于时态聚类模糊综合评价的基金评级算法
孟志青,金诗思
(浙江工业大学 管理学院,浙江 杭州 310023)
近年来,中国基金市场呈指数级增长,每年有数百只新基金进入市场,中国银河证券基金研究中心发布的2019年上半年基金模块快报显示:截至2019年6月30日,中国共有135 家公募基金公司,共管理基金数量5 547 只,管理基金资产净额达134 053.99 亿元,份额规模达127 536.31 亿份。面对如此庞大的基金市场,对基金进行有效评级,提供每个基金的正确评价对投资者们如何选择优秀的基金项目进行投资非常重要。基金评级是基金评级机构搜集信息数据,运用特定的评级方法对基金的投资收益和风险,以及基金管理人的管理能力进行综合分析,并通过使用具有特殊意义的符号和数字文字向投资者们展示分析后的基金优劣排序结果,评定的基金等级可为投资者提供重要参考。目前,中国基金评级行业仍在发展中,中国评级市场整体处于较为混乱的状态,评级方法良莠不齐,且一些基金评级机构利用虚假评级结果吸引投资者的资金流入,导致一些投资者的资金严重损失,破坏了基金市场的健康发展。因此,为了保护投资者的利益,建立一套公正、客观和科学的基金评价方法,对金融投资市场的健康发展具有重要的理论意义和实际价值。
1 基金评级现状
基金(含股票型基金)的评价方法多种多样,国内外学者对证券选择和基金评价方法进行了许多研究。早在1952年,Markowitz[1]提出了均值-方差证券组合投资模型,首次给出了证券投资选择的一种理论方法。随后Treynor(1965),Sharpe(1966)及Jensen(1968)提出了证券与基金评价历史上的三大经典指标:夏普指数、詹森指数和特雷诺指数,对金融投资领域产生了深远的影响[2-4]。1966年,Treynor等[5]提出的T-M模型在资本资产定价模型的基础上增加了一个二次项,以衡量基金择时能力和选股能力。但Henriksson等[6]在对美国116 只基金进行实证研究后得出了不一样的结论,他们认为基金经理不具有择时能力,并在T-M模型的基础上提出了H-M模型,将基金择时能力定义为基金经理通过预测市场收益与无风险收益之间的差异以调整投资组合的系统风险的能力。1984年,Chang等[7]充分考虑了市场在上升期和下降期这两种情况,提出了衡量基金经理择时能力的C-L二次项模型,其实本质上和H-M模型并无区别。
中国对基金评价的研究大多基于国外已经提出的指标对中国基金进行实证研究。范慧慧等[8]、曾祥渭等[9]先后提出了基于AHP的投资基金绩效综合评级模型,对投资基金风险、收益、择时选股能力、绩效持续性和资产运作能力等13 个指标进行了权重分析,发现收益率水平、风险水平和绩效持续性水平权重较大。赵小玥等[10]则提出了一种多因子差值绩效评价模型,并与已有的三因子模型进行了比较,结果表明:该模型可以较好地衡量基金的绩效表现,基金样本的投资组合表现较差,实际投资风格趋同,基金经理人大多缺乏控制风险的能力。朱青[11]利用层次聚类法对中国开放式基金的风险进行综合评级,并通过随机森林算法构建了基金综合风险评级模型。杜金岷等[12]应用国外的研究成果,选取其收益率指标、风险指标、Jensen指数、Treynor指数、Sharpe指数以及T-M模型与H-M模型等对15 只偏股型开放性基金进行实证研究,结果表明中国开放式基金的基金经理没有突出的择时能力。徐新扩等[13]将绿色证券投资基金作为研究对象,使用国际通用基金评价方法,将选取的若干只绿色证券投资基金与沪深指数300进行对比分析。杨霞等[14]在2019年提出投资基金体系应该将投资者的调研时间成本考虑在内,因此构建了包含基金实力、市场风险和基金经理能力等三层基金业绩评价体系。除此之外,廖华等[15]将数据包络分析(DEA)应用到基金业绩评价中,对2002年的46 只证券投资基金的相对绩效进行了评价。在传统数据包络分析法(DEA)中,所有的决策单元(DMU)都由有限观测样本组成,2016年,李春龙[16]解决了DEA有效性受到小样本和内部依赖性干扰的问题,重新构建了Bootstrap-DEA绩效评价模型,对中国30 支开放式基金2008—2010年的经营业绩进行实证研究,结果表明在基金评级中Bootstrap-DEA模型更合理,更具可靠性。
综上,国内外学者都提出了不少基金评级方法,但是许多基金评级方法采用的是静态评级方法,很少有学者在基金的时间属性评级指标上研究出评级方法。因为基金数据其实是一种时态数据,并在不断地变化当中,所以基金评级方法的评级结果是否稳定可靠对投资者来说十分重要。但是笔者研究发现:根据任何基金评价方法得到的结果都很难满足评级的稳定性,主要原因是数据在不同的时间点上不具有稳定性。为了克服这种时间不稳定数据的影响,希望能够通过基金时态数据在时间粒度上的变形,对基金评价随着时态变换进行评价,从而得到一个有效、可靠和稳定的评级方法。为此,笔者建立一种新的基于时态聚类模糊综合评价的基金评级算法(TCF算法),利用模糊综合评价法对多个指标分析的科学性与可行性,选取特定指标,对某一段时期的某一行业基金的不同时态数据进行评价,然后与现有的评级机构进行比较,发现笔者所提算法在时间变化时评级结果具有较好的准确性和稳定性。
2 相关理论简介
2.1 基金评价体系
当前,已有的基金评级方法主要存在随着时间变化基金指标数据实时变动导致评级结果存在不稳定性和不够准确的问题。为了解决这个问题,选择晨星、济安金信、银河证券、天相投顾、海通证券和招商证券等评级机构的常用评级指标,提出新的时态模糊综合评级方法,保证在相同指标体系下进行比较。
晨星基金的评级对象仅限于成立3 年及3 年以上的基金,货币基金和资本担保基金除外;晨星评级采取先分类再评级的步骤,先对具有3 年业绩的基金进行归类,在同类基金中按照“晨星风险调整后收益”(MRAR)指标从大到小排序,前10%被评为5 星;接下来22.5%被评为4 星;中间35%被评为3 星;随后22.5%被评为2 星;最后10%被评为1 星。MARA作为晨星评价的核心指标,以期望效用理论为基础,该理论认为相对于不可预期的高收益,投资人会更倾向于可预见的低收益,愿意用一部分预期收益来换取收益明确的收益。晨星会根据每支基金在评价期间的月度回报率进行调整,波动越大,惩罚越多,从而体现基金月度收益的波动情况。晨星评价核心指标MARA的计算式为
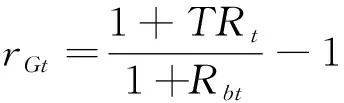
济安金信作为金融软件提供商,相比其他评级机构而言更具独立性。济安金信的评级步骤首先通过定性分析和风格漂移测算对基金公司和基金进行合规性检验,随后在同类基金业绩、基金基准和基金投资标的基础上进行定量评价,从基金本身、基金经理和基金公司等3 个方面对基金进行评价,并秉持科学严谨、全面维度和客观公正的原则,从10 个维度考察基金和基金公司的综合实力,即盈利能力、效益稳定性、抗风险能力、选择股票能力、基金选择能力、选择时间能力、指标跟踪能力、超额收益能力、总体成本和规模等是否合适(适用于公司),随后进行权重科学配置,最终进行类内基金星级评价。
银河证券则从投资管理能力、规模管理能力和定性评价等3 个方面对基金进行评价,且3 个方面的权重不同,分别取50%,30%,20%。银河证券采用定性分析与定量分析相结合的方法,在定量分析中加入了定性分析,定量评价的指标主要是基金的基本表现评价指标,如单位净值、净值增长率、标准差、贝塔系数、可决系数、三大经典指数和换手率等指标。定性评价则是对基金公司治理结构、投资研究与交易、市场营销、运营与管理等的综合评价。总体来看基金公司采用收益评价指标、风险评价指标和风险调整后收益等3 个指标来评价基金。在风险评估指标方面,银河公司将基金净增长率的标准差转化为自己的评级标准分;在盈利能力评估指标方面,公司主要考虑基金在评估期内的净增长率、季度净增长率和月度平均净增长率,并将这些指标转化为银河设计的标准分数,综合计算,标准得分越高,基金的盈利能力越好。从风险调整后的收益率指标来看,风险调整后的收益率评价的标准分可以由以前盈利能力评价的标准分减去风险评价的标准分得出。因此,风险调整后的收益评价得分越高,基金的整体业绩就越好。
总之,各家评级机构大多采用综合评价方法对基金进行打分,并按分数排名按比例划分基金评级,采用的核心指标大部分都为风险调整后收益指标,不同的是对个别指标的选取和评价方法。综上将选择使用上述3 个基金机构的评级指标:平均收益率、夏普指数、特雷诺指数、詹森指数、收益率标准差、TM-选股能力和TM-择时能力等7 个指标对基金进行综合评价并给出笔者的评级,具体指标公式和计算方法介绍如下。
2.2 时态数据
由于基金数据是一种含时间的时态数据,那么评级方法应该根据随时间变化的时态数据给出评级,以保证评级的有效性和可靠性。时态型概念由C.betti首次提出,孟志青等[17]对其进行了系统性的研究,对时态型、时间粒度及时态因子都作了相应的数学定义,同时提出了时态关联规则挖掘的多个模型,包括单事件、多事件和事件的周期性关联问题。时态型模型的思想实质上是将时间按一定长度划分,将数据按时态型进行变形。很多时候很难发现时间序列数据在其原有时态型上的规律,若对其进行一定的时态转换变形,会发现意想不到的规律。如在经济系统中有许多非平稳数据,经过差分变形可变为平稳数据,由此得到有意义的模型结果。基金评价其实是对历史数据的一个分析综合,其业绩一般具有持续性,那么利用时态变形的方法,期望得到稳定性和准确性较好的评级方法。下面首先给出时态型相关定义介绍。
将现实世界的时间看作一条无限的实数轴,轴上的每个点表示一个绝对时刻,轴上的每个区间表示一个绝对时间,一个绝对时间是绝对时刻的一个集合,由此给出关于时态型μ的定义。
定义1假设μ是从绝对时刻t到绝对时间的集值映射,即R→2R,如果μ满足下列性质:
1) 非空性,t∈μ(t)。
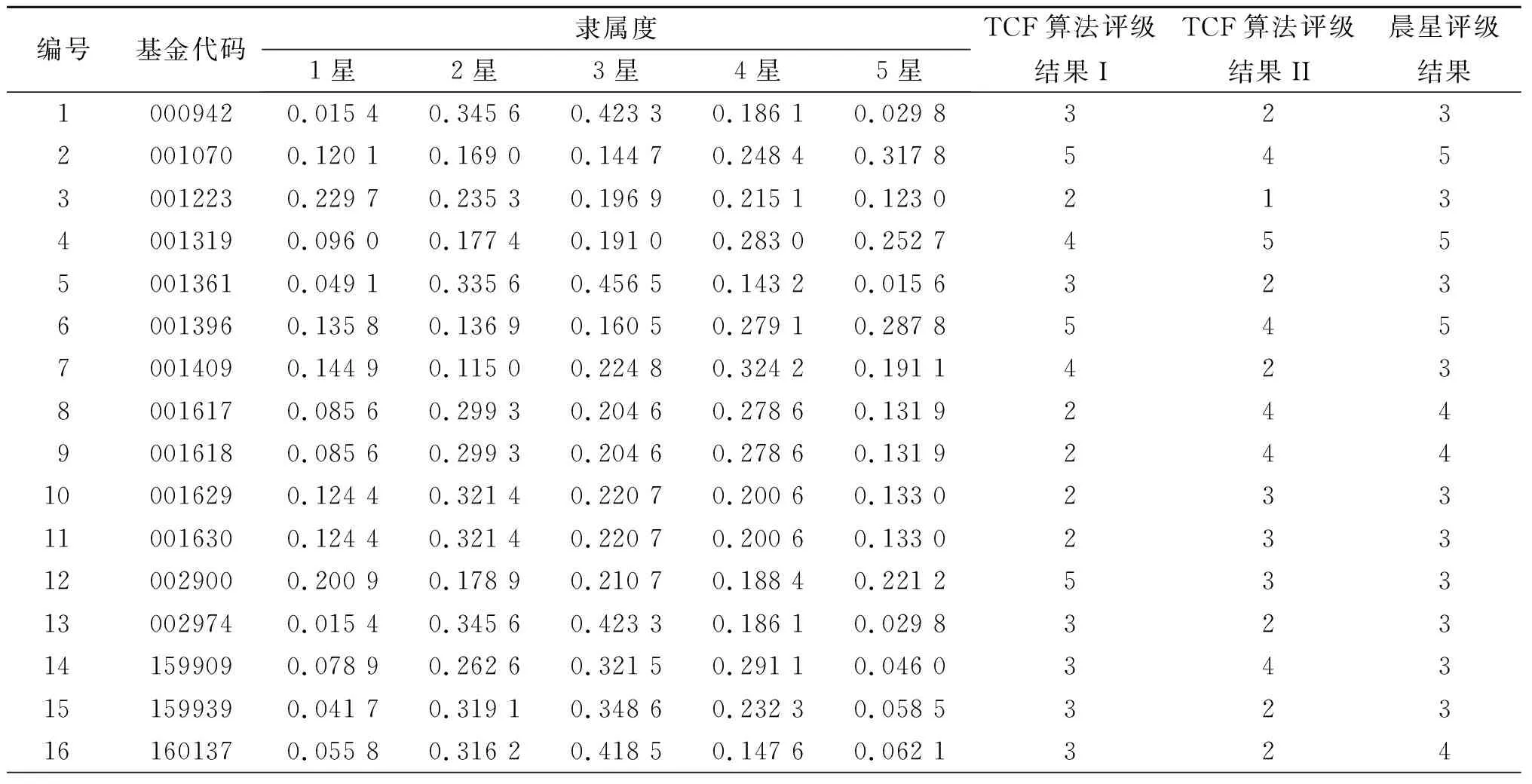
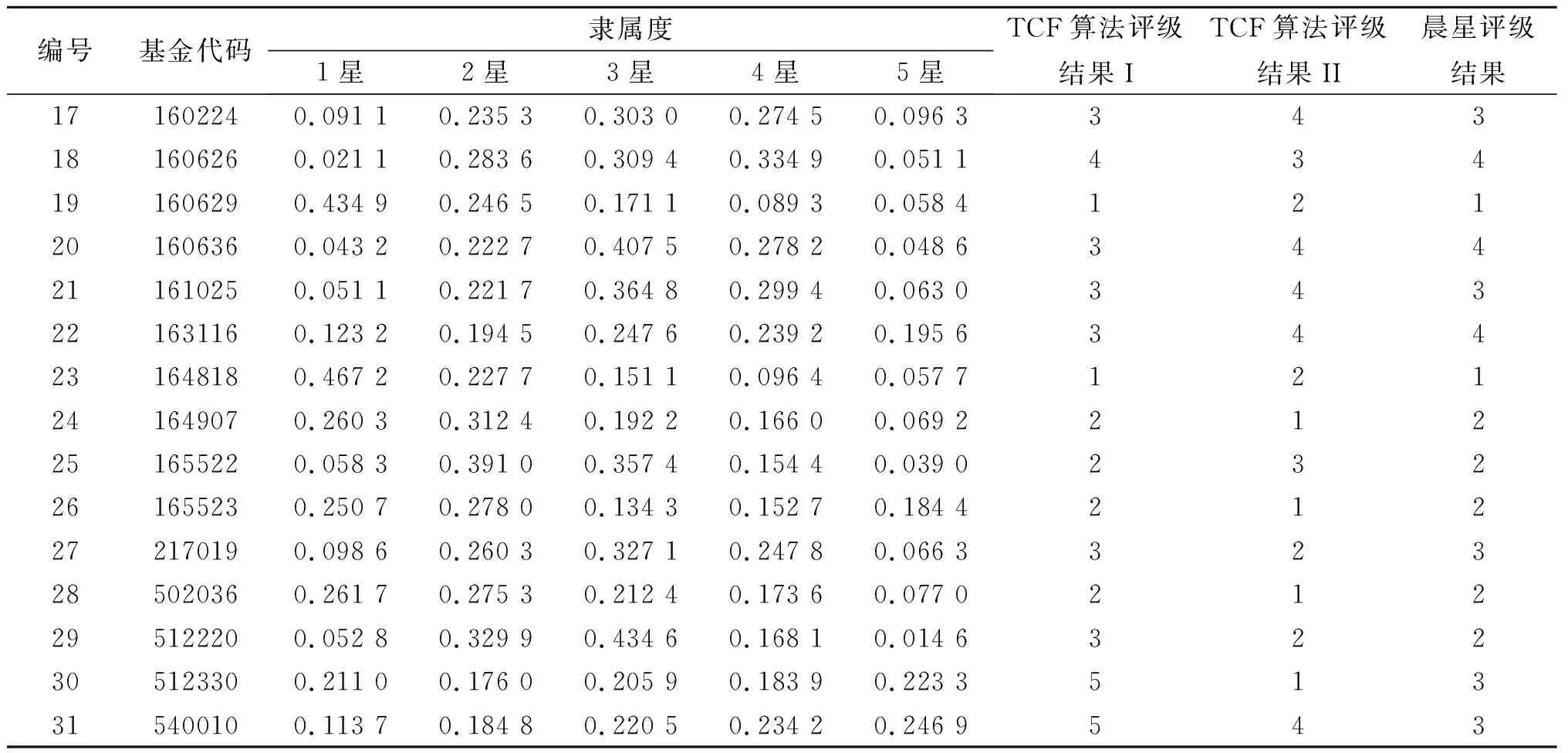
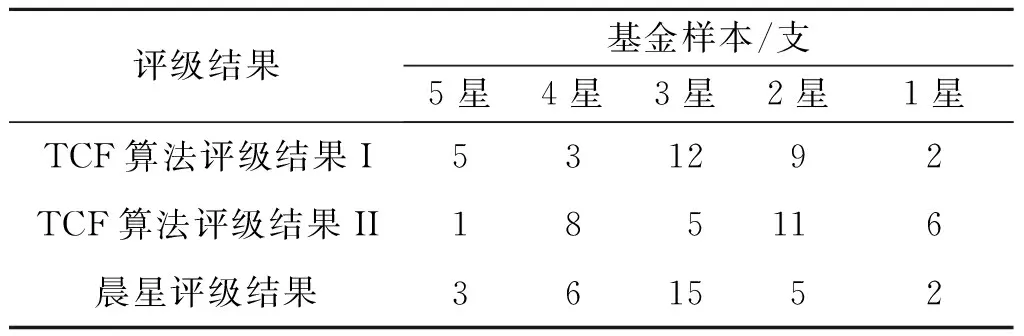
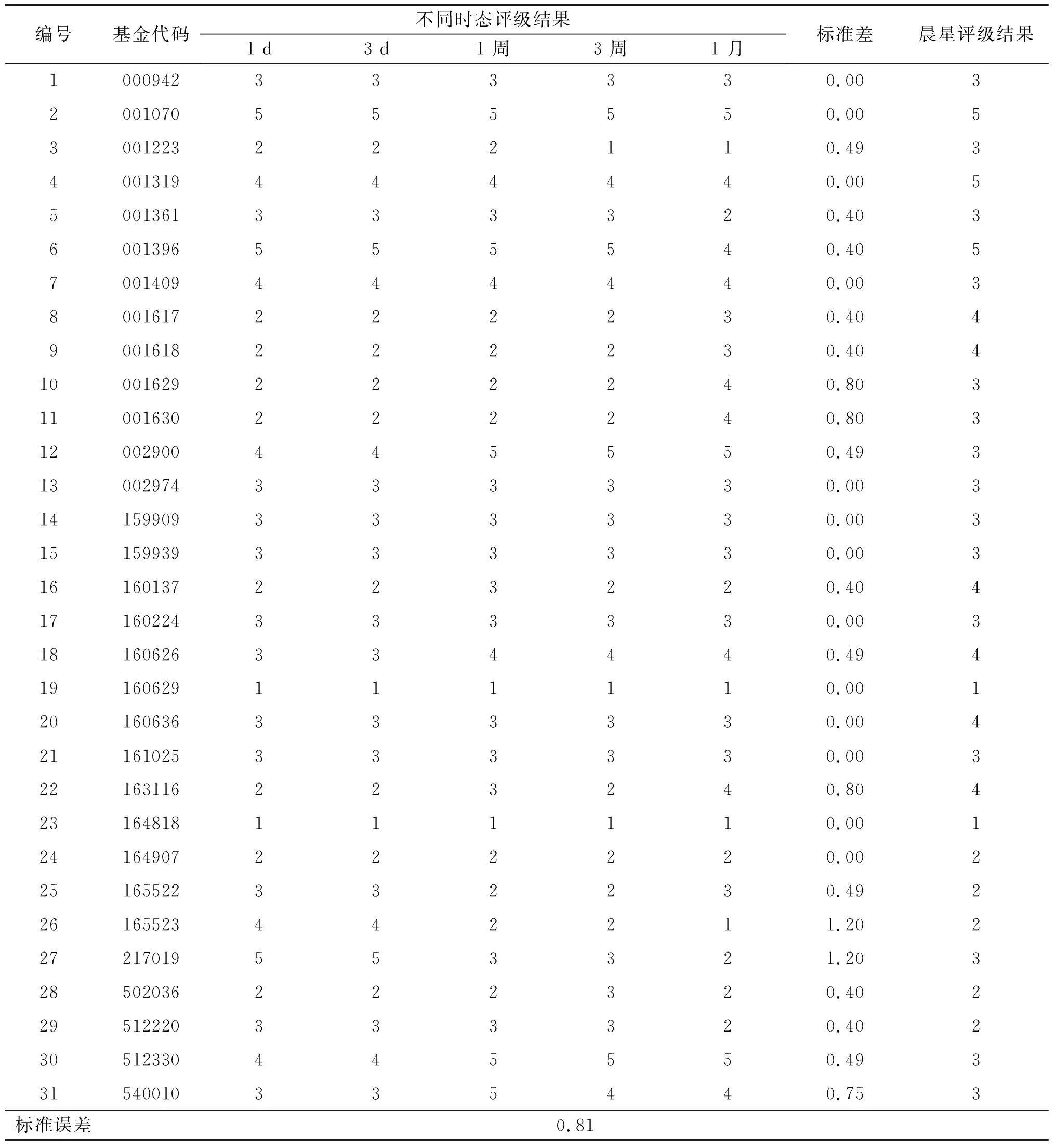
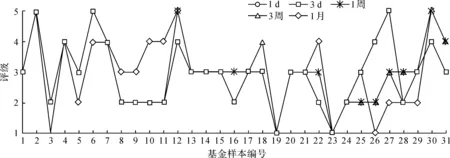
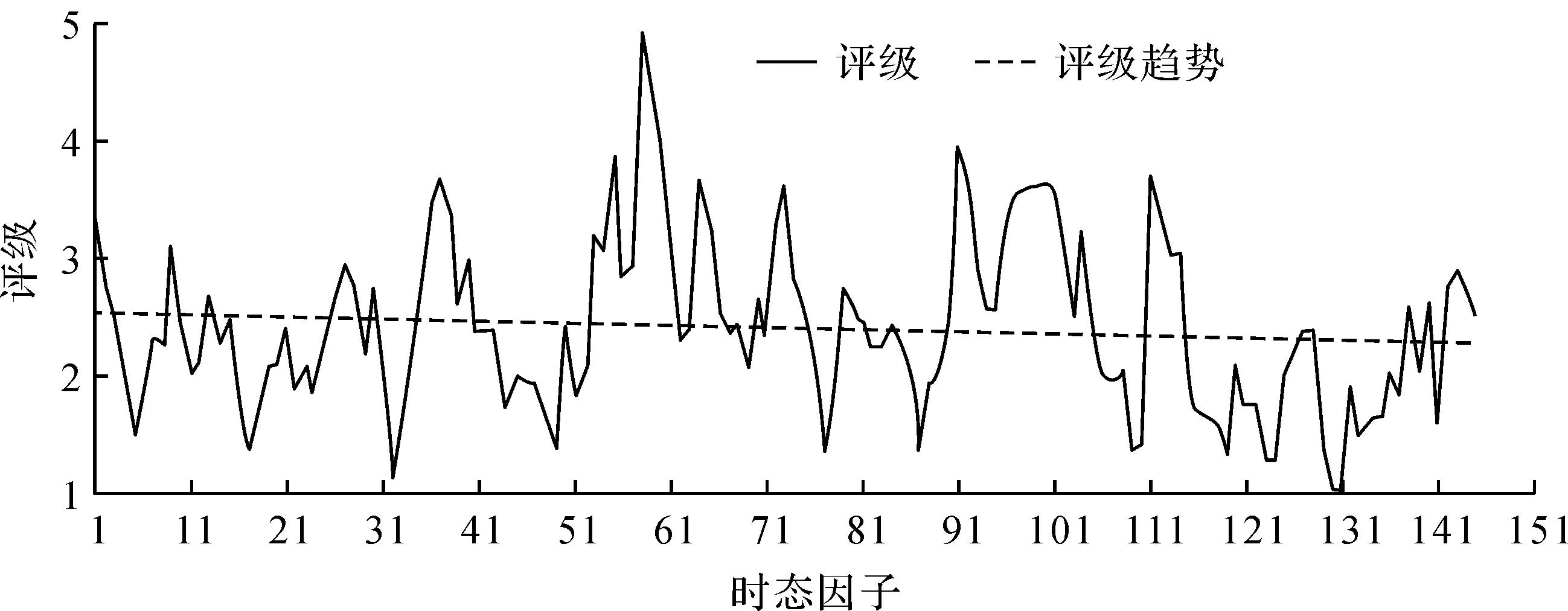
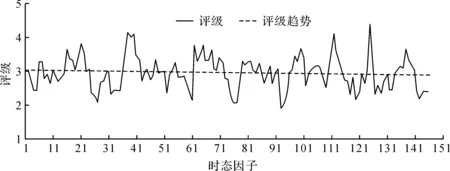
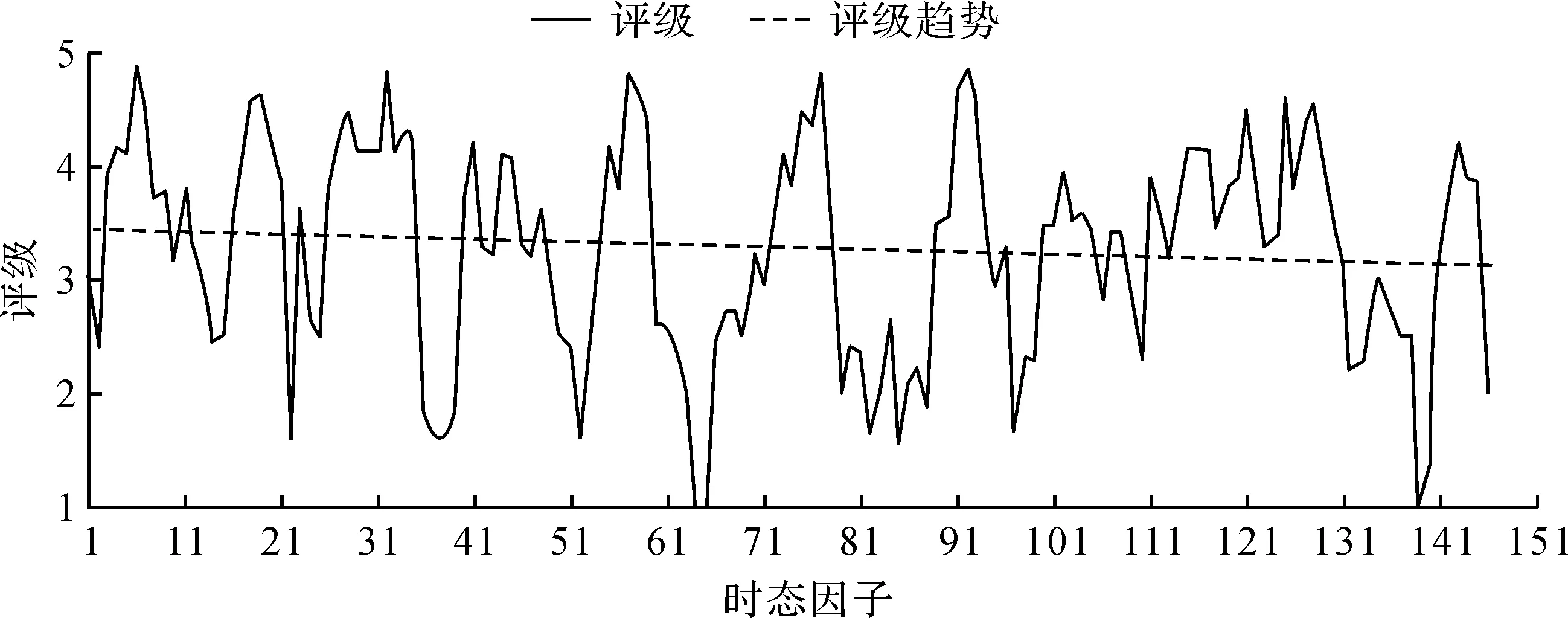
2) 单调性,若t1 3) 同一性,∀t′∈μ(t),μ(t′)=μ(t)。 4) 有界性,∀t′∈μ(t),|t′|<+∞。 则称μ为时态型,μ(t)为μ的时态因子。 按照定义1,时态型μ是对时间轴的划分,时态因子μ(t)是绝对时刻的集合,生活中常见的时态型有秒、分、小时、日、周、月和年等[17]。针对所涉及的问题,时态型有如下两个性质: 性质1若t1≠t2,则μ(t1)∩μ(t2)=Ø或μ(t1)=μ(t2)。 性质1表明时态数据划分时时态因子是不重叠的,保证时态数据综合后的无关性;性质2表明时态数据在一个时间区间上可以用有限个时态因子有序排列,保证在用时态型分析数据时的完整性。因此,利用时态数据模型给出一个基金数据的时态型划分,然后使用模糊综合评价法提出一个新的评级方法,可以保证不同时态型的评级稳定性。 定义3假设μ为一个时态型,若μ的每个时态因子的绝对长度相等,则可以称μ为一个时间粒度;若μ的所有时态因子的绝对长度可以分为有限几类,则称μ为一个粗时间粒度,年和月就是典型的粗时间粒度。 模糊综合评价的评级方法就是在两个时间粒度上提出来的。 模糊评价是描述现实生活中不精确现象的有效评价方法。模糊综合评价是对具有多种属性或是受多种因素影响的事物作出一个合理的,综合所有因素的总体评价。其特征概括为模糊性、定量性和层次性3 个方面。模糊性是指该综合评价的结果是一个集合,可以较为准确地刻画事物本身的模糊状况。定量性是指事物具有各项指标来衡量其不同方面,具有不同的本质特征、价值体系和评价尺度。而层次性则是指标之间具有层次性,需要建立指标分级体系来综合处理指标,保证模型的科学性和可行性。在众多的模糊方法中,模糊综合评价法被广泛地应用在许多科学领域。在股票基金方面,有很多研究者将模糊理论与其他算法结合评价预测股票基金,殷洪才等[18]应用模糊神经网络来预测股价,范慧慧等[8]则根据熵权法和层次分析法确定综合权数,对基金业绩进行综合评价。笔者的研究不同于以上的工作,通过改进模糊综合评价法解决模糊矩阵中隶属度主观性较强的问题,嵌入时态型,并给出模糊综合评价法。 模糊综合评价模型定义为在一个时态型μ下的模糊指标体系:FCE(μ)=(U,V,R(μ),A),其中各个符号的意义如下。 2.3.1 指标因素集U 指标因素集U={u1,u2,…,ui,…,um},其中m为指标个数,元素ui代表影响评价对象的第i个因素。 2.3.2 评价集V 评价集V={v1,v2,…vj,…,vn},其中n为评价类别(分级)个数,元素vj代表第j种评价(分级)结果。 2.3.3 关于时态型μ的模糊评价矩阵R(μ) 时态型μ的模糊评价矩阵R(μ)为 (1) 式中rij表示指标ui对评级vj的隶属度。R(μ)的值随时态型的不同而不同,因此最终的评级结果受时态型变化的影响。 2.3.4 指标的权向量A B(μ)=A∘R(μ)={b1(μ),b2(μ),…,bj(μ),…,bn(μ)} (2) 式中:bj(μ)表示样本对评价类别vj的隶属度;∘表示综合模糊算子。通常bj(μ)为 (3) 对于一个评价对象,给出不同时态因子μ下对应的模糊评价指标体系FCE(μ)(U,V,R(μ),A),通过上述计算可得到该评价对象对每个类别的隶属度,最后的评价结果根据最大隶属度确定。 在模糊综合评价中最主要的问题就是确定每个指标对评级的隶属度。正确地确定隶属函数是运用模糊集合理论解决实际问题的基础,隶属函数是对模糊概念的定量描述,在实践中确定隶属度函数的方法是多种多样的,目前还没有统一的模式。一般都是根据经验或统计来确定的,也可以由专家建议得出,即专家评价法,但其存在评级结果主观性较强的缺点。在基金评价中,寻找专家并对每只基金进行评价不太符合实际,也耗费了大量人力物力,更重要的是专家评价法在一定程度上存在主观性。故笔者尝试利用每个时态因子下的基金指标数据作为数据样本,分析每个时态因子下的聚类结果,在指定时间区间内统计出每一评级出现的百分比,即隶属度。即该算法的提出是以一个时态因子内数据的聚类结果来取代在模糊综合评价中的专家评分,利用数据的客观性将模糊综合评价法中求取隶属度的环节客观化。建立的TCF算法主要包括指标体系构建、时态数据转换和基于时态聚类的隶属度求解等过程。 选择中国5 个著名机构的基金评级机构:晨星开放式基金评级、济安金信基金评级、上海证券基金评级、天相投顾基金评级和银河证券基金评级的共性指标,分别从绩效、风险调整后收益、风险和基金经理等方面出发,选出7 个指标,得到指标因素集X={u1,u2,u3,u4,u5,u6,u7},如表1所示。 表1 基金评级指标集Table1 Fund rating index set 平均收益率是指复权单位净值增长率在评价期间内的算数平均值。标准差则是单位净值增长率评价期间内的标准差,衡量基金收益率的稳定性,一般来说其值越大,收益率波动性越大,基金具有较大投资风险。 夏普指数是衡量基金每承受一单位总风险所能获取风险收益大小的指标,其计算式为 Sp=(Rp-Rf)/δp 式中:Sp表示夏普指数;Rp表示基金在考察期中的平均收益率;Rf表示在考察期内的平均无风险利率;δp表示基金收益率标准差,也被称作基金总风险。 特雷诺指数是衡量基金每承受一单位系统风险能获取风险收益大小的指标,其计算式为 Tp=(Rp-Rf)/βp 式中:Tp表示特雷诺指数;Rp表示基金在考察期中的平均收益率;Rf表示在考察期内的平均无风险利率;βp表示基金承受的系统风险。考虑同类基金,相对Tp大的基金其绩效表现会更好,与夏普指数同理。 詹森指数是衡量基金投资组合收益率与相同系统风险下市场投资组合收益率差异的指标,是一种绝对绩效指标,其计算式为 Jp=Rp-[Rf+βp(Rf-Rm)] 式中:Jp表示詹森指数;Rm表示市场收益。一般来说,当不同基金之间进行比较时,基金詹森指数较大者更好。 T-M模型衡量基金经理的选股能力和择时能力,其计算式为 Rp,t-Rf,t=αp+β1(Rm,t-Rf,t)+ 式中:αp表示基金经理选股能力指标;β1表示基金组合所承担的系统风险;β2表示基金经理择时能力指标;Rp,t表示基金在t时期内的平均收益率;Rm,t表示市场在t时期内的平均收益率;Rf,t表示基金在t时期内的无风险收益率;εp,t代表误差项。 在选出表1中的7 个指标后,采用层次分析法(AHP)中的两两比较矩阵确定各指标的权重。两两比较矩阵虽然仍含有主观成分,但它不把所有因素放在一起比较,而是采用成对比较的方法,并且采用相对尺度,尽可能减少因各因素性质不同所带来的比较问题上的困难,从而给出相对准确和一致的各指标权重结果。 首先,构造各指标间的两两比较矩阵S。比较指标选取1~9,用sij表示第i个指标对第j个指标的比较结果。例如s12=3表示第1个指标在与第2个指标作比较时,在1~9的相对重要程度中,量化值为3,表示第1个指标比第2个指标稍微重要。对表1中的指标构建两两比较矩阵S,即 (4) 相应的比较顺序为平均收益率、夏普指数、特雷诺指数、詹森指数、标准差、选股能力和择时能力。 其次,在构造出两两比较矩阵后,求出其最大特征值λ=7.778 3。两两比较的结果可能造成A比B重要,B比C重要,而C又比A重要这种不一致的结果,因此需要进行一致性检验。一致性指标为 式中:λ为两两比较矩阵的最大特征值;n为指标个数。一致性比率为 式中RI可通过查表得到。当CR<0.10时,则通过一致性检验。现将λ=7.404 8,n=7代入,查表得到n=7时RI=1.32,计算得CR=0.095 4,即通过一致性检验。 最后,将最大特征值对应的特征向量归一化后,得到 A={0.147 0,0.426 2,0.082 4,0.253 7,0.026 9, 0.018 0,0.045 9} (5) 以式(5)作为平均收益率、夏普指数、特雷诺指数、詹森指数、标准差、选股能力和择时能力的权重。 选定时态型后,原始数据中对于映射后的第k个时间段,任意一个基金在第i个指标下都会有q/l个指标值,且只与当前时态因子u(tk)有关。为了合成该时态型下的时态数据,需要将这q/l个指标值映射成一个综合指标,一般映射方法为求平均法,故针对基金样本的指标集U=(u1,u2,…,um),设某个基金在[T1,T2]时间段内的原始指标数据D为 (6) (7) 对于第k个时间段的第j个指标,有 (8) 即表示在时态因子μ(tk)下,该基金的指标数据。除此之外,也可以采取时间型线性或指数加权平均,即越靠近当前评价时刻的时间权重越高,权重整体呈线性或指数分布。 图1 TCF算法的流程示意图Fig.1 Flow chart of fuzzy comprehensive evaluation method based on temporal clustering (9) 最终可以得到各评价对象对于各级隶属度F∈Rp×n,其中对于每个fih,有 (10) 对于每支基金样本,采用最大隶属度对应的类别作为该基金的评级。 综上,TCF算法实现步骤为 步骤1建立基金评级体系。根据基金评级机构的评级方法,建立一套基金评价体系,得到7 个评价指标X={x1,x2,x3,x4,x5,x6,x7},随后利用层次分析法中的两两比较矩阵求出指标权重向量A={a1,a2,a3,a4,a5,a6,a7}。 步骤2数据预处理。选定基金样本P与基金评级区间[T1,T2],根据所建立的基金评级体系,选取其所有评价指标数据,对样本数据进行筛选删除,并对个别指标数据进行正相化处理,得到基金原始指标数据D。 步骤6综合评价。应用步骤1求得的指标权重向量对评价矩阵中的隶属度进行加权平均,得到所有基金样本对各评级的隶属度F∈Rp×n,根据最大隶属度法得到基金样本在评价期内的最终评级,然后与基金评级机构的评级结果进行对比分析,还可以改变时态选择得到最优算法。 在对大部分评级机构的评级方法进行分析后,发现其共同的特点都是对基金先分类后评级,且基金运作已满3 年,因此在科技、传媒及通讯等行业的股票基金中选取31 支基金样本作为研究对象,其评价区间为2016-11-28—2019-11-25,数据资料来源于wind资讯、晨星评级官网以及中国基金网。 利用python软件对所有指标数据进行预处理并编写代码实现TCF算法,对基金指标数据进行分析得到基金评级结果。基金对象集为P={P1,P2,…,P31},指标集U={u1,u2,…,u7},[T1,T2]=[2016-11-28,2019-11-29],出于对证券交易市场周末休市的考虑,选择“1 周”作为时态型,将评价区间划分为连续的146 个时间段,即l=146,为方便与评级机构进行对比,选取的聚类数为n=5,将基金样本分为5 类,即评价集V={v1,v2,…,v5}。 确定TCF算法参数后,运行模型程序算法得到所有基金样本在5 种分类上的表现和属于各类别的隶属度情况,并与晨星评级结果作相应的比较。晨星作为国际基金评级的权威机构自身没有基金和股票投资的业务,保证了评级和分析的独立性和客观性,再加上近几年晨星在本土化方面作出了许多努力,在国内的认可度极高,是一个很好的参考对象,具体情况如表2所示。由表2可知:晨星评级结果与TCF算法评级结果存在较小的差异,大致存在一个级别的误差。从表2还可以看出:晨星评级结果与TCF评级结果I存在较小的差异,在31 支基金样本中17 支基金样本的TCF评级结果与晨星评级相同,有10 支基金样本的TCF评级结果与晨星评级结果在上下一个类别范围浮动,仅有4 支基金样本的TCF评级结果与晨星评级结果相差2 级,这是符合实际情况的。通过表2不仅可以判断出基金倾向相邻评级的程度,利于投资者判断选择,还可以较为直观地对比TCF算法的分类结果与晨星评级结果。 表2 TCF算法基金评级结果与晨星评级结果对比Table 2 Comparison between fund rating results based on TCF and morning star rating results 表2 (续) 通过TCF算法将基金样本分为5 类,分别用5星、4星、3星、2星、1星来表示,其中被评为5星的基金最值得投资。3 种基金评级结果的具体分布情况如表3所示。表3中的数字表示该评级结果中被归为5星的基金样本数量,在晨星评级结果中有3 支基金样本被评为5星,TCF算法评级结果I中有5 支基金样本被评为5星。在TCF算法评级结果II中仅有1 支基金样本为5星,其被评为4星的基金样本数量相对多于晨星评级结果和TCF算法评级结果I。总的来说,表3中评级结果II同评级结果I与晨星评级结果相差较大,而评级结果I同晨星评级结果大致相同。 表3 TCF算法评级结果与晨星评级结果的分布情况对比 因在短期内基金的质量好坏只能通过其未来业绩表现来判断,为了检验TCF分类算法对基金样本的评级是否合理准确,笔者采用未来一个月中基金样本的复权单位净值增长率来衡量TCF算法分类基金是否合理,复权单位净值考虑了红利再投资的因素对基金净值进行复权计算,能够较为真实地反映基金业绩,评价期内复权单位净值增长率越高,基金在评价期内的业绩越好。据此,笔者计算了TCF算法评级和晨星评级在2019年11月29日至2019年12月31日各分类结果的平均基金份额复权单位净值月增长率,对比结果如表4所示。由表4中可知:TCF算法评级结果I整体与晨星评级结果相似,4星的复权净值增长率最高,1星的复权净值增长率反而比2星的复权净值增长率要高,但TCF算法评级结果II在接下来的一个月业绩表现随星级呈现依此递减分布,类别之间差异明显,具有较好的分类效果,因此也说明TCF算法基金评级结果II在基金选择投资方面更具参考性,也说明了TCF算法的基金分类结果的合理性,在基金评级中具有较好的适用性。 表4 不同基金评级方法下未来一个月各类别的复权单位净值增长率Table 4 Growth rate of net unit value of fund resumption of various types in the coming month under different fund rating methods 为了更好地研究TCF算法的性能,判断该算法在基金评级时的稳定性,选取多个时态型进行试验,得到了不同时态下TCF算法的基金评级结果,并定义某支基金在不同时态下的基金评级结果为Y=(Y1,Y2,Y3,…,Ys),使用标准差来衡量TCF算法的稳定性。标准差定义为 (11) (12) 各时态评级结果与各基金评级结果的标准差见表5。为了更直白清晰地观察31 支基金样本在不同时态型下TCF算法评级结果的变化,绘制了基金评级变化折线图,其结果如图2所示。 表5 TCF算法在不同时态型下的基金评级结果对比Table 5 The fund rating results of TCF under different tenses 图2 31 支基金不同时态型的3 年基金评级Fig.2 Three-year fund ratings of 31 funds for different tenses 由表5可知:基金001070(编号2)在不同时态下的基金评级结果相同,说明该评级具有强稳定性,同时该评级结果也与晨星评级一致;有一些基金样本如001223(编号3)在“1 d”“3 d”“1 周”等3 个时态下的评级一致为2,而在“3 周”“1 月”等2 个时态下评级为1,评级并不稳定,从侧面说明选取一个合理的时态型可以提高基金评级结果的质量。由图2可知:大部分的基金样本在不同时态下评级结果为重合状态,部分基金样本在不同时态下评级发生变化,且大部分仅变为相邻的评价,计算所有基金样本的评级变化程度平均标准差为0.35,并且计算得到晨星评级结果的标准误差为0.81,比较可知通过TCF算法得出的基金评级结果稳定性相对较好。因此TCF算法评级算法在不同时态型下的评级结果具有较好的稳定性,且时态型的选择对基金评级的影响较小。 再来看单只基金在评价期内每个时态因子下的评级变化,选取综合评级分别为1,3,5的3 支基金进行评级变化分析,如图3~5所示。基金160629(编号19)的总体评级为1,通过观察图3可以看出:其评级波动幅度较大,但趋势一直趋于2。基金000942(编号1)的综合评级为3,从图4中可以看出:其评级变化较为稳定,一直保持在3左右,呈微微下降趋势。从图5中可以很明显地看出:基金001070(编号2)在评级期内的评级波动较大,虽大多在高评级之间来回波动,但还是存在大幅度波动的情况。由此说明:基金评级并不能代表全部,还是存在一定的风险,投资需谨慎,相较于基金评级机构的评级方法,TCF算法为投资者提供了基金在评价期内的评级变化,更能够帮助投资者全面地了解基金,减少投资失误。 图3 基金160629的3 年评级变化Fig.3 Three-year rating change of fund 160629 图4 基金000942的3 年评级变化Fig.4 Three-year rating change of fund 000942 图5 基金001070的3 年评级变化Fig.5 Three-year rating change of fund 001070 通过对基金数据在时间粒度上的变换,建立了TCF算法。TCF算法旨在从另一个角度为广大投资者或基金评级机构提供参考或建议,其实证研究仅选取了31 支基金样本作为研究对象;同时,还可以选择其他类型的基金,如股票型、债券型基金进行综合评价,可供投资者和基金研究者灵活使用。TCF算法也可以根据需求,针对不同的侧重点建立不同的基金评级体系,得到不一样的基金评级结果并进行对比。同时,笔者还引入了时态数据,融合聚类分析和模糊综合评价法,通过客观数据计算出隶属度,避免了主观因素对基金评级结果产生的不良影响,并利用了基金指标数据的时间属性,使该算法得出的基金评级结果更有效、更可靠。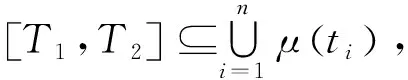
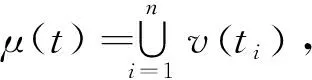
2.3 模糊综合评价
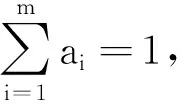
3 TCF算法的建立
3.1 基金评级指标体系构建
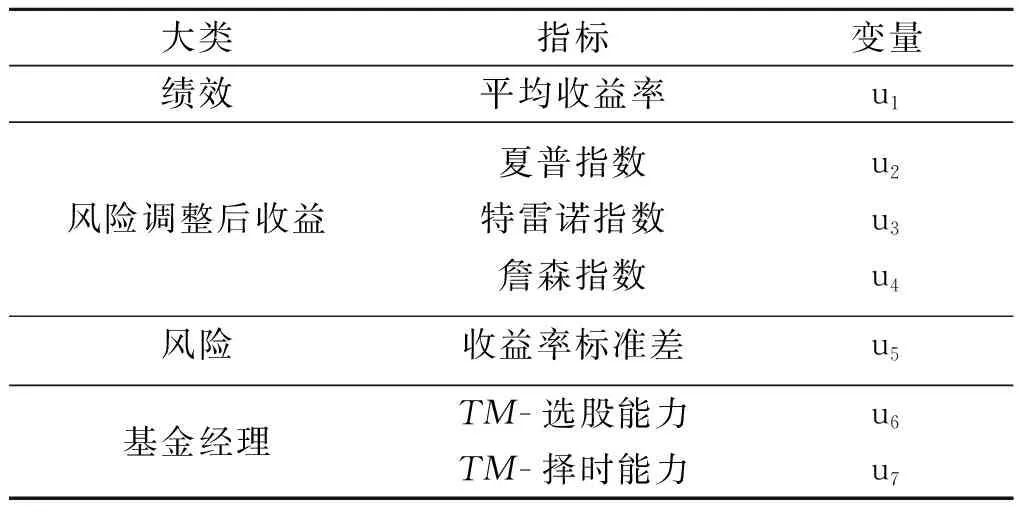
β2(Rm,t-Rf,t)2+εp,t3.2 时态数据转换
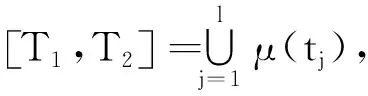
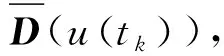
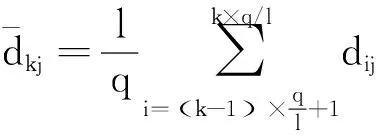

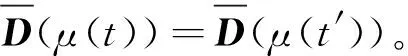
3.3 基于时态聚类的隶属度求解
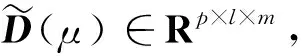
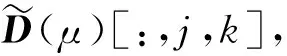
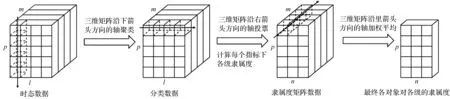
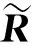
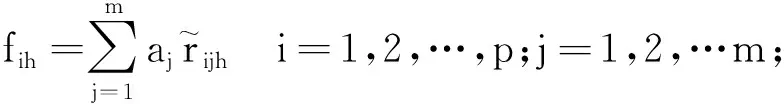
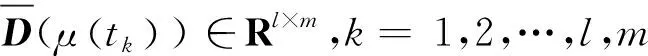
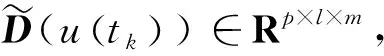
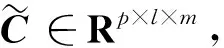
4 实证研究
4.1 研究对象及数据获取
4.2 基金评级结果与分析

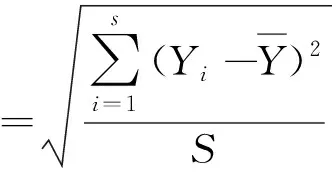
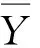
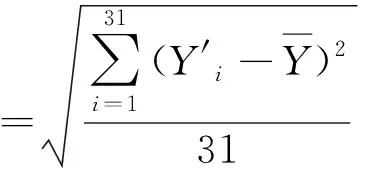
5 结 论

