一种基于卷积神经网络的雷达干扰识别算法

刘国满，聂旭娜 (北京理工大学 信息与电子学院，北京 100081)

随着现代战争的信息化发展，雷达的地位变得更加不可替代，而基于数字射频存储器 (DRFM) 的欺骗干扰技术的出现，使得雷达的正常工作遭到了前所未有的威胁[1].作为现代战争之眼，如何在复杂的电磁环境下采取恰当的抗干扰措施是至关重要的，而抗干扰的前提是能够正确识别这些干扰.

目前，基于机器学习的干扰识别方法主要关注点在于信号的特征参数提取[2-4]，它着重分析不同干扰信号在各个变换域特点，从中提取不同的特征参数，设计不同的分类器对有源干扰类型进行识别.如梁金弟等[3]、李娜[4]在提取了干扰信号时域、频域、时频域等多维特征后，分别选择支持向量机和BP神经网络实现雷达干扰信号识别；郝万兵等[5]提取了干扰信号时频图像矩阵的奇异值，采用支持向量机进行识别；魏煜宁等[6]则将模糊C均值聚类融入到决策树中，设计出一种自动的决策树识别方法.这些方法都基于干扰的特征参数，只是用到的分类器有所区别，但是由于特征参数只是在小样本情况下信号分布规律的总结，人工特征选择又有可能引入实验者主观因素，得到的结果不一定符合整体规律，导致模型泛化能力较差.但利用特征训练分类器是值得肯定的，理论上，只要提取的特征足够强，识别效果就会相对较好，因此，目前最大的困难是解决特征问题.

当然，也有一些学者选择了卷积神经网络作为分类器，如SHAO等[7]直接利用干扰信号数据训练一维的卷积神经网络，但是卷积神经网络的处理依靠的更多是数据的空间关系，一维的网络结构相对不易进行训练识别.WANG等[8]和LIU等[9]均提取了干扰信号的STFT时频图像作为训练集训练卷积神经网络，取得了不错的识别效果，但是STFT图像分辨率低，不易观察到频率的细微变化.

除此之外，在以上文献中或者无法识别拖引干扰，或者单纯采用一个周期提取的特征参数对拖引干扰进行判断，结果存在很大的偶然性.目前，有效的抗拖引干扰方法为记忆波门跟踪法，即利用干扰出现之前测得的速度值确定跟踪波门的移动速度，以有效抗干扰，也有学者张建中等[10]基于STFT时频图像实现了抗间歇采样转发干扰.本文受到前人思路启发，选择提取时频图像，直接从产生原理上分析信号应有的时频分布，避免了特征参数提取不合理的问题；并提出了两个卷积神经网络级联的干扰识别方法，分别利用单周期时频图像和多周期合成图像，实现了单周期预分类、多周期细分类的干扰识别模型，得到了更高的识别率.

1 干扰数据产生与时频特性分析

雷达的典型干扰样式有以下几类，分别是窄带瞄准、宽带阻塞、灵巧噪声、多假目标、间歇采样转发、距离拖引、速度拖引以及距离速度联合拖引干扰八种.但是卷积神经网络因其结构原因更适于识别二维图像，而不是这种一维的信号，并且如果单独采用干扰信号的时域或频域信息进行网络训练会造成信息的损失，因此需要对信号进行一定的处理.而时频分析法可以从根本上获得信号时频域分布特征，从而使提取的特征更有普适性和代表性.

在时频分析方法中，最常见的非短时傅里叶变换莫属，但是窗长的限制使其时频分辨率受到很大影响，而且它只适用于分析缓变信号，无法敏感分析突变信号.为了获得更高的频率分辨率，本文选择Wigner-Ville分布[11]来计算时频图像，这是一种Cohen类时频分布，不仅解决了频率分辨问题，而且具有真边缘性、平移不变性等优良特性，但是其对多分量信号存在交叉项干扰.为了减小交叉项的干扰，常用的处理方法是加窗，对τ加窗得到的是伪Wigner-Ville分布，对t和τ分别加窗得到的是平滑伪Wigner-Ville分布.

为了比较各种时频分布的优劣，这里采用脉宽10 μs，带宽30 MHz，采样频率100 MHz的线性调频信号做参考，仿真过程中包含两个间隔200 m的目标，设置频率单元个数为2 048，并通过多次实验选取各种方法的最佳窗长，得到的时频分布图像如图1所示，其中，短时傅里叶变换、Wigner-Ville分布、伪Wigner-Ville分布、平滑伪Wigner-Ville分布的计算耗时分别为0.27 s、0.86 s、0.32 s和3.4 s.观察图像可以发现，短时傅里叶变换分辨率较低，当目标距离较小时信号易出现粘连；Wigner-Ville分布分辨率很高但是交叉项严重且无法分辨哪个信号是交叉项；平滑伪Wigner-Ville分布虽然效果最好，但是其耗时过长，约为其他方法的10倍，也不宜采用；伪Wigner-Ville分布相比Wigner-Ville分布分辨率略有降低，但是在减小了计算量的同时减弱了交叉项.综合考虑后，最终选择伪Wigner-Ville分布生成干扰信号的时频图像.

图1 各种时频分析方法对比Fig.1 Comparison of various time-frequency analysis methods

对于信号s(t)，其伪Wigner-Ville分布(简称PWVD)的定义如下：

(1)

式中：h(τ)为窗函数，本文采用汉宁窗;t代表时间;τ代表时间积累量.

为了获得上文提到的几种干扰样式的时频分布，首先要对信号进行仿真，假设雷达发射信号带宽3 MHz、脉宽100 μs、采样频率30 MHz.根据以上雷达参数，设置相应干扰参数进行仿真并生成数据集，具体的干扰参数范围如表1所示，在此范围内选择12组参数，分别在干信比0～10 dB情况下每间隔1 dB仿真获取5个干扰样本，这样每种干扰信号可以得到12×5×11=660个干扰样本，然后对信号样本进行伪Wigner-Ville变换，经去噪处理及信号检测后生成最终数据集.图2即为不同干扰信号在干信比5 dB情况下，经上述处理得到的时频分布图像，其横轴代表信号时长，纵轴代表信号频率.对所有干扰样本进行上述处理后即可得到本文所需数据集.理论上讲，训练一个卷积神经网络需要足够多的数据样本，但是不论对于实采数据还是仿真数据获得巨大的样本都是非常困难的.于是本文通过对信号的检测、缩放等预处理过程，使得不同带宽、脉宽以及重频下的信号展现出近乎相同的特性，不同的干信比和干扰参数的设置又能增加模型的泛化能力，这大大降低了对训练样本数的要求.

表 1 雷达与干扰参数设置

分析这些时频图像可知，无干扰情况下，很容易检测到雷达线性调频信号，且多周期内信号的频率不会发生较大改变.窄带瞄准干扰和宽带阻塞干扰都覆盖了信号的全时域，其唯一的区别就是干扰信号与目标信号的相对带宽不同，这在图2(a)中有着很好的体现.灵巧噪声干扰由于既要在时域对目标信号进行覆盖，又要在频域产生多假目标的欺骗特性，因此干扰信号要能够在时域展宽，在频域完全覆盖住目标频率.间歇采样转发干扰要对雷达信号分时交错进行采样和转发，因而与目标信号叠加后的时频图像会呈现图2(e)的不连续性.多假目标干扰则是通过不同的时延产生多个距离假目标达到欺骗雷达的目的.对于图2(g)(h)(i)中的3种拖引干扰来说，初始拖引时刻，其延时和频率并不会发生很大变化，不易区分，随着时间推移，虽然其时频图像渐渐发生更大的变化，但是又会与单个的假目标干扰产生混淆.显然，对于拖引干扰，仅仅依靠单帧图像进行识别是行不通的，因而本文在后续的识别过程中利用多周期信息进行判断.值得注意的是，本文为了更高的分辨率选择了伪Wigner-Ville分布，随之而来的交叉项则是不可避免的，以上时频分布图像中均出现了不同程度的交叉项干扰，如图2(f)中的1个真实目标与5个假目标之间均产生了一定交连，但信号所独有的特征是不变的，因而并不会影响后续的识别过程.

图2 不同干扰与目标混合信号PWVD时频图像Fig.2 PWVD time-frequency images of mixed signals with different jammings and target

2 分类器结构设计

卷积神经网络以其强大的分类能力而备受关注，它不需要额外的特征提取过程，只需将带有标注的样本数据输入网络就能自动的利用卷积层提取图像特征，提取的效果远高于人工特征.事实上，卷积神经网络通过卷积核进行特征提取的过程，从某种程度上来讲是一种对图片样本进行特征拟合的过程，拟合的效果则由网络权值来决定.

此外，出于对计算量及所需分类数目的考虑，本文选择了两层卷积、两层池化来构建神经网络，具体结构如图3所示.网络的输入是大小为100×100的灰度图像，输出层为Softmax函数，输出节点数依据分类的类别数设置.第一层采用6个大小为5×5的卷积核，第二层为16个大小为5×5×6的卷积核，分别经过2×2和4×4的均值池化后进入全连接层，全连接层也有两层，分别有120个、84个节点.当然，这里也可以加深网络层数提取不同干扰时频图像中更深层次的特征，但这需要更大的计算量，实验证明，该结构足以满足本文对不同干扰信号的分类任务.

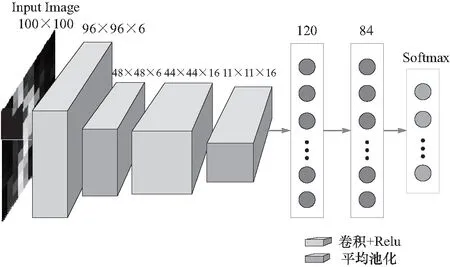
图3 卷积神经网络结构Fig.3 Structure of convolutional neural network

本文中提到拖引干扰无法依据单周期信息区分，在初始拖引时刻会被误判为无干扰，在拖引后期则又与单个的假目标干扰相同.针对这一问题，本文提出了利用两个卷积神经网络级联的方式来识别各种干扰类型.在这一过程中，需要对每一个网络单独进行训练，以此来完成多种干扰的分类任务.初次判断时先将单个PRI内的拖引干扰、单假目标干扰及无干扰3种情况分为一大类，融入时间信息后再对具体的干扰类型进行二次判断，整体识别流程如图4所示，即首先对信号进行伪Wigner-Ville变换，然后通过去噪、信号检测及灰度化等操作，将处理好的图片送入第一个卷积神经网络，如干扰类型单周期可识别则直接输出结果，否则将间隔一定时长的两个PRI内的时频图像合成一张，送入第二个神经网络进行识别.

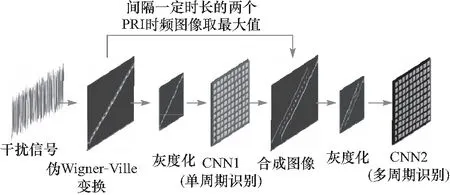
图4 干扰识别整体流程图Fig.4 The overall flow chart of jamming recognition

具体处理图像过程如图5所示，以间歇采样转发干扰为例，首先对图像进行去噪，设置噪声剔除门限为时频分布最大值的5%，经过去噪处理后获得一个脉冲重复周期内的时频图像，而需要识别的信息可能只占图像的一部分.因此，本文还需要进行信号检测，设定一个阈值由外向内与时频图像中的每一行及每一列进行比较，找到信号边界，从而获取有用的图像信息.这样处理既能放大各种干扰之间的差异，又能减小识别过程的计算量，有利于提高识别正确率.之后，将彩色图像灰度化，并将图像大小缩放至100×100，这样可以进一步减小计算量，提升识别速度.训练网络时还需要对每种干扰类型进行独热编码(one-hot encoding)，它是分类变量作为二进制向量的表示，除了编号的索引被标记为1之外其余都是零值，它的优点是可以处理类别间不具有大小关系的特征.

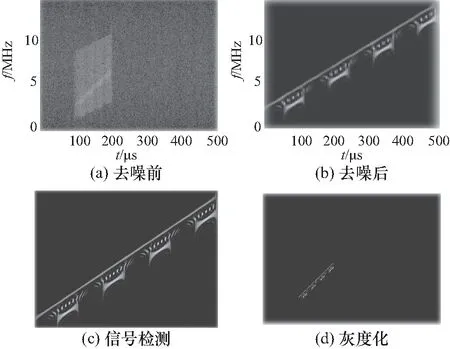
图5 图像处理过程Fig.5 Image processing

经过图像处理后就可以开始训练模型，文中将不同干信比下产生的6种干扰(3种拖引干扰、单假目标干扰及无干扰暂不作区分)信号的时频图像，每种660张，共计3 960张图片随机划分为训练和测试集完成第一个卷积神经网络的训练.其中，每种干扰包括训练集500张，测试集160张，训练完成后即可识别这6种干扰样式.至于拖引类干扰具体属于哪一种拖引，还需要结合其时延和多普勒频移信息才能做出判断，由于单个脉冲重复周期内的时频图像包含的信息不充分，因此本文利用合成时频图像进行识别，即一旦判断为拖引干扰，则提取间隔一定时长的两个PRI内信号的时频分布图像，比较两幅图像信息，取对应位置的最大值作为最后的合成图像，3种干扰的合成时频图像如图6所示.

图6 拖引干扰合成时频图像Fig.6 The synthetic time-frequency image of gate pull off jamming

通过比较3种拖引干扰的时频图像可以明显看出，距离拖引干扰在间隔一段时间的两个PRI之间发生了较大的时延；速度拖引干扰则发生了多普勒频移，但相对于整个干扰信号带宽，发生的频移较为微小；而距离速度联合拖引干扰则同时具有以上两种特性；至于无干扰或者单个的假目标干扰的情况，合成图像与原图相比不会发生变化.据此可以训练第二个卷积神经网络来识别拖引干扰.同样的，对每种干扰样本随机选取500张作为训练集，其余160张作为测试集进行实验.

3 仿真结果分析

为了对实验结果进行更全面的评价，本文分别从模型识别正确率、算法鲁棒性、计算复杂度以及干信比对识别正确率的影响4个方面对本文提出的算法进行评估.

3.1 识别正确率测试

识别正确率是评价实验结果最直观的指标，本文采用混淆矩阵进行分析，混淆矩阵的每一列代表预测干扰类型，对每一列求和得到的是预测为当前干扰类型的样本总数，每一行代表真实干扰类型，对每一行求和得到的是真正属于该类干扰的样本总数.混淆矩阵中编号所对应的干扰类型如表2所示，借助混淆矩阵可以更清楚的知道干扰类别的误判情况.

表2 各干扰样式对应标号

图7显示了实验样本在训练集和测试集上得到的混淆矩阵，其中，黑色代表识别正确率，灰色代表识别错误率，颜色越深，相应的正确/错误率越高，观察矩阵的识别情况，可以发现卷积神经网络在训练集和测试集上均取得了较高的识别正确率，整体可达98%以上.分析混淆矩阵可知，分类错误的情况主要包括以下两类:1)信号时频图之间的相似性，如灵巧噪声与多假目标干扰在时间轴上的覆盖范围都较宽，间歇采样与拖引干扰在某些参数情况下与单独的线性调频信号相比差别较小；2)干信比的影响，如窄带瞄准干扰在低干信比情况下更易受到噪声的影响，从而使得干扰带宽展宽，误判为宽带压制干扰.

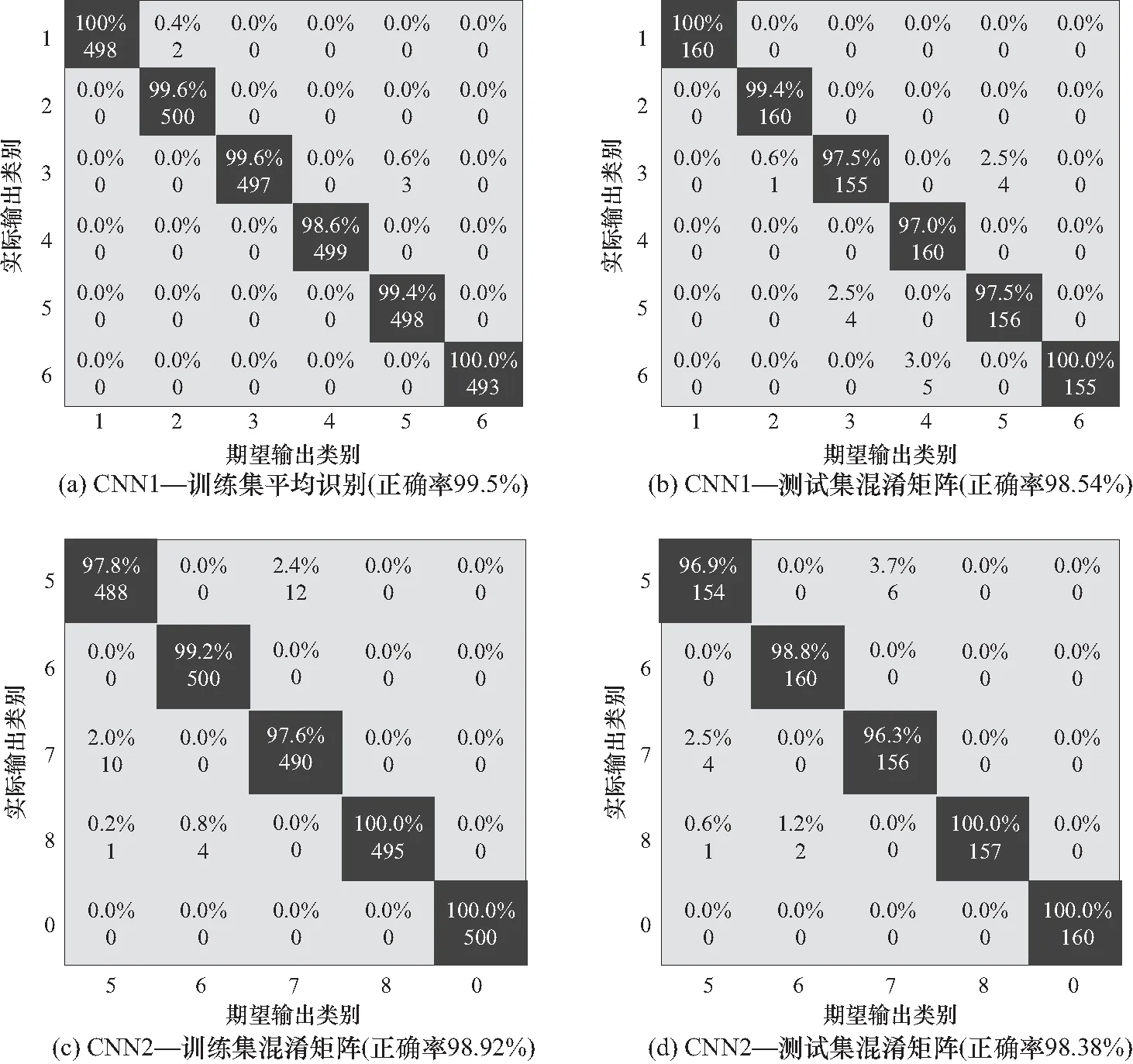
图7 实验结果混淆矩阵Fig.7 Confusion matrix of experiment results

3.2 鲁棒性测试

雷达干扰信号以其特殊性，很难像其他种类识别一样，建立庞大而完善的数据集.为了说明本模型训练方法不需要庞大的样本量且不依赖于样本参数的设定，本文首先利用原始数据集，从中随机选取不同数量的训练样本对干扰识别正确率进行评估，所得结果如表3所示.之后本文重新设置了另一组雷达参数与干扰参数产生新的训练样本，此时，雷达带宽30 MHz，脉宽10 μs，重频10 kHz，采样频率200 MHz，干扰参数依据此时的雷达参数设置，仍旧在最佳干扰参数范围内选取12组参数生成训练集，所选择的参数尽量做到全面.训练方法与上述过程相同，分别计算各种干扰样式在每个数据集中的干扰识别正确率、总体分类精度以及Kappa系数，所得结果如表4所示.

表 3 训练样本数对识别正确率的影响

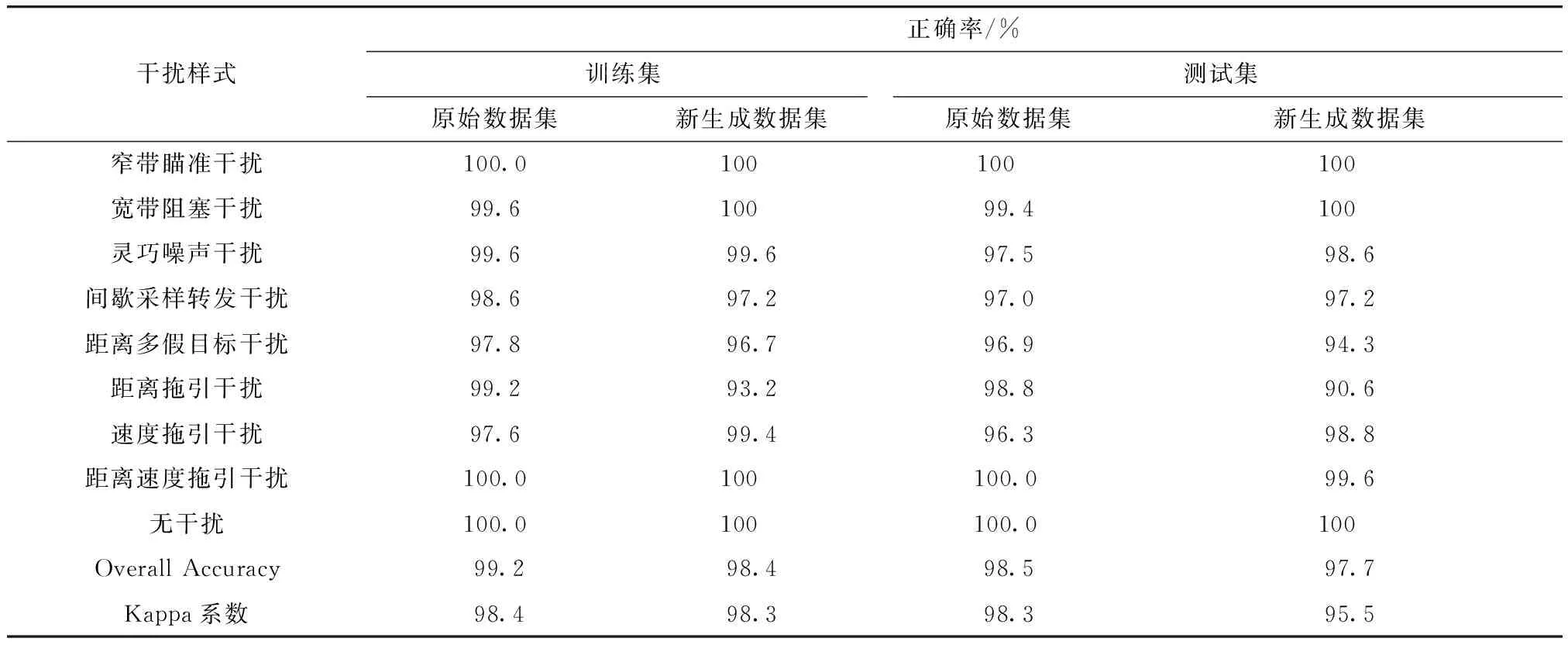
表4 不同数据集对识别正确率的影响

如表3所示，本文测试了不同训练样本对识别正确率的影响，实验结果表明，在训练样本数为100时，总体识别精度可以达到94.83%，Kappa系数为93.8%，与本文用到的500个干扰样本训练出的模型相比，总体识别精度下降了4.39%，Kappa系数下降了4.55%，但是仍然保持在90%以上，据此可以说明本文提出的模型在小样本情况下依然能够获得较高的识别率.而在使用新的数据集对模型进行测试后可以发现，更改训练集前后模型的识别正确率并无明显变化，由此可以得出本文提出的训练方法不依赖于样本参数的设定.综上，本算法在训练样本数较少、更改数据集参数的情况下，仍能获得较好的识别性能，这对雷达系统有着重要意义.

3.3 计算复杂度评估

计算复杂度是衡量系统分类性能的重要指标，在本文提出的干扰识别算法中，主要计算量集中在两部分，一是信号伪Wigner-Ville分布的计算，二是卷积神经网络的识别.仿真运行环境中，CPU为i5-6200U，运行内存12 GB，选择不同长度的信号分别测试PWVD计算时间和CNN识别时间，每种测试重复10次，记录平均计算时间，得到的数据如表5所示.

由表5可知，在一次干扰识别过程中，主要的运算量集中于信号的PWVD变换，信号越长，计算量也越大，而本文所用的卷积神经网络平均只需要0.008 4 s即可给出识别结果，因此在后续的研究过程中将会考虑优化信号的PWVD计算.

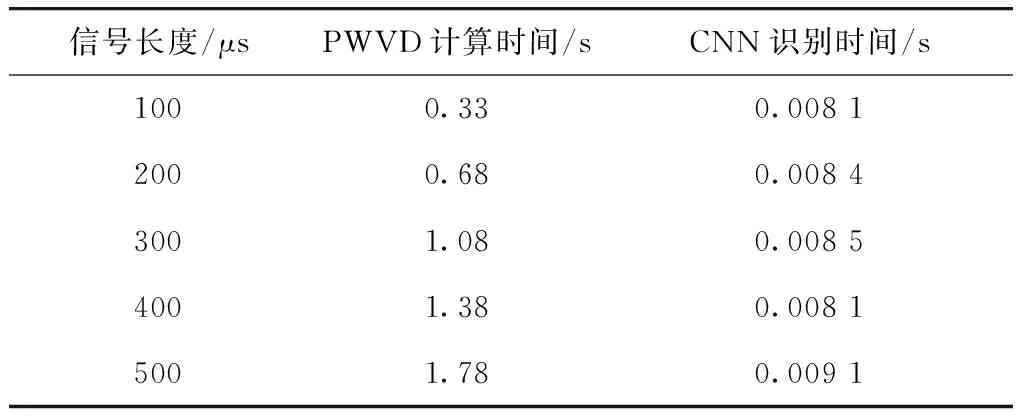
表 5 不同长度信号的计算时间

3.4 干信比测试

本文具体研究干信比对识别正确率的影响，为了使识别结果更具有说服力，本文选取了训练集中不包含的雷达参数与干扰参数，此时，雷达带宽4 MHz，脉宽80 μs，重频2.5 kHz.在不同干信比条件下，进行20次蒙特卡罗仿真，分别统计针对脉冲压缩雷达的噪声类干扰和欺骗类干扰情况下的识别正确率，得到的识别结果如图8所示.

图 8 干扰识别率随JSR变化曲线Fig.8 The curve of jamming recognition rates changing with JSR

由图8可知，在当前仿真条件下，噪声类干扰的识别正确率在JSR为0 dB时就能达到100%，在实际情况中，压制类干扰功率很高，识别也相对更容易进行.欺骗类干扰识别所需干信比要更高一些，尤其是拖引类干扰，由于多普勒频移相对较小，需要JSR大于3 dB时才能达到85%以上的识别正确率.据此可得，提高干信比可以提高识别正确率，且该模型对噪声类干扰识别效果非常好，即使在低干信比情况下也能顺利识别，有着很高的识别正确率和良好的泛化能力.

4 结论

本文针对一般干扰识别方法中人工特征提取所包含的信息不全面、参数选择受主观因素影响大、识别率较低等问题，将信号的时频分布图和卷积神经网络运用到干扰识别工作中，使得8种干扰样式在整个数据集上的总体识别精度达到了98%以上.这归功于以下两个方面:一是信号的伪Wigner-Ville分布既衰减了交叉项的影响又有着较高的分辨率，使得它能从根本上获得信号的时频域联合特征；二是级联的卷积神经网络能够分别利用单周期信息和多周期信息对干扰类型进行判别，有着更强大的分类能力.相比目前的机器学习方法，该方法在干扰识别的种类和识别率上都有着明显优势.虽然该算法在实时性方面尚存在一定不足，但相信随着技术的发展与算法的优化，问题一定会得到解决.