基于Stribeck模型的制动系统动力学分析

王 宇，孙战里

(1.安徽汽车职业技术学院，安徽 合肥 230601；2.安徽大学 人工智能学院，安徽 合肥 230039)

随着汽车技术的日益更新和人类生活水平的提高，人们对汽车的安全性、可靠性、舒适性、排放性能等提出了更高的要求[1]。然而，因为道路拥堵，在汽车刹车时产生的噪声与振动对乘坐的舒适性和汽车的经济性等使用性能产生了很大的影响[2]。汽车制动振动和噪声的产生主要是由粘滑振动导致的[3]，而系统摩擦副之间的摩擦因数又是导致粘滑振动的主要原因[4]。国内外学者已经对盘式制动器制动时产生的振动与噪声进行了大量的实验和广泛而深入的理论研究。BOWDEN等建立以滑块-传送带的单自由度模型，以及K POPP等对制动器进行研究，得到了与MILL相似的结论，肯定了负斜率机理的重要性[5-6]，同时发现粘滑运动及其原因。大多数的粘滑振动现象，其本质都是干摩擦导致粘滑振动。基于此，多名学者通过建立不同的力学模型，研究干摩擦诱发的粘滑振动、分岔与混沌现象，其中能够较好说明粘滑本质的是滑块-传送带模型。此外，YONG LI在对传送带模型进行分析时找到了系统中存在的稳定极限环和混沌，并预测了在较低的相对速度下运动有发生粘滑振动的可能性[7]。通过实验，U.ANDREAUS发现相对速度与摩擦力呈负相关和摩擦模型的滞回效应[8]。刘丽兰等以单自由度系统为对象，分析改变法向压力对极限环幅值的影响[9]。HINRICHS N等用鬃毛模型替代了库仑摩擦，研究接触刚度中切向刚度与阻尼的关系，建立了含有外部激振和摩擦的质量块-传送带系统，改变分叉参数影响系统的位移，粘滑现象与外部激振相关，出现了高维周期解[10]。SINOU J J等在恒定摩擦系数的情况下，建立的Sprag-slip非线性模型[11]，研究系统参数对系统的稳定性和振动幅值影响。陈思雨等在SINOU的基础上引入非光滑非线性的Stribeck摩擦系数模型，通过研究得出系统的工作、结构参数对系统的动态性影响[12]。但是这些模型都只考虑了摩擦块的切向运动，忽略了制动块的端面跳动对制动颤振的影响，而根据余卓平的研究，制动盘的端面跳动也是导致制动抖动的主要原因之一[13]。为了更全面地表现制动器制动时的动力学行为，本文在前人研究的基础之上添加了摩擦块与制动盘之间的轴向刚度和阻尼来表征制动盘的端面跳动，并分析了制动器结构参数对制动性能的影响。

1 模型的建立

综合考虑制动块的切向振动和端面振动，本文将盘式制动器系统简化为双自由度质量块—传送带模型(见图1)。

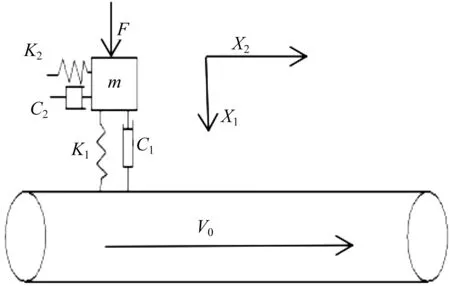
图1 质量块-传送带双自由度模型

其中，X1,X2分别表示制动块的轴向位移和切向位移;K1,K2分别表示作用在制动块的轴向总刚度和切向总刚度;c1,c2分别表示作用在制动块的轴向总阻尼和切向总阻尼;m代表制动块的质量;V表示传送带的速度;F表示作用在制动块上的作用力;f表示摩擦块受到的摩擦力。

根据牛顿第二定律，可以建立动力学方程如下：

(1)

(2)

式中：u—制动块与传送带之间的摩擦系数。

2 Stribeck干摩擦模型

目前应用最多的干摩擦模型有库伦模型、Dahl模型、Stribeck模型、GMS模型[14]等。本文选Stribeck模型，该模型属于形式简单、易于调整、具有平滑处理的指数形式的模型。其表达式[15]为：

μ(vr)=[μk+(μs-μk)e-α|vr|]sign(vr)

(3)

其中，μk—动摩擦因数;μs—静摩擦因数；

α—指数衰减因子，反映了负斜率的大小；

vr—两运动件之间的相对运动速度。得出μ-vr的特性曲线见图2。

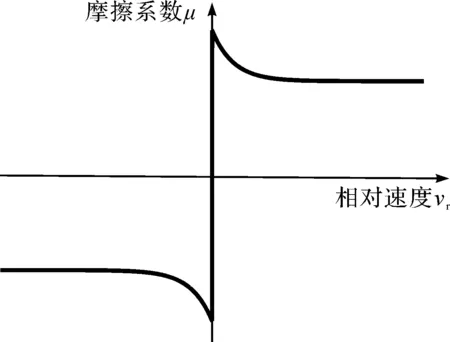
图2 指数形式的干摩擦模型

3 数值分析

方程(1)汽车制动颤振的基本方程的数值解，可为进一步了解及研究制动系统产生的非线性振动提供理论参考。通过运用龙格-库塔法求方程的数值解，可以分析、讨论制动器的振动特性，同时对制动压力、初始速度、摩擦模型衰减因子对系统非线性振动的影响规律进行研究。本节以某品牌国产车为例，选取系统参数数值m=1 kg，k1=1.1 e5N/m，k2=1.3 e5N/m,us=0.6，uk=0.35，c1=c2=1 N·s/m。

3.1 制动压力的影响

保持制动系统结构参数和制动初速度不变，对制动压力进行改变，在相图和时域图中观察制动压力对制动系统动力性能的影响。如图3所示(部分选图)，通过数值仿真，本节得到制动块的切向和轴向相图以及时域图(v0=0.05 m/s)，分析可得如下结论：

(1)制动压力很低(50 N)时，系统做纯滑动的自激振动并处于混沌状态(图3(a));

(2)当制动压力增长到200 N时，系统仍做无周期的混沌运动，但是从相图中可以看到此时系统产生了粘滑振动，但是粘着时间很短以致无法分辨(图3(b))。

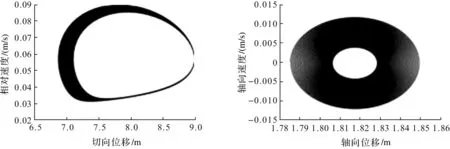
图3 不同制动压力下的相图、时域图

(3)随着制动压力的继续增长(700 N)，系统振动具有严格的粘滑特性，但此时已由混沌振动变为多周期振动，并可以从时域图中看到每个周期的粘着时间大概为0.05 s。

(4)制动压力继续增长到1 500 N,系统开始做单周期粘滑振动，粘着时间大概为0.125 s。

3.2 初始速度的影响

保持结构参数和制动压力不变，不断改变制动初速度，在相图和时域图中观察制动初速度对制动系统动力性能的影响。如图4所示，通过数值仿真，本节得到制动块的切向和轴向相图以及时域图(部分选图)，分析可得如下结论：

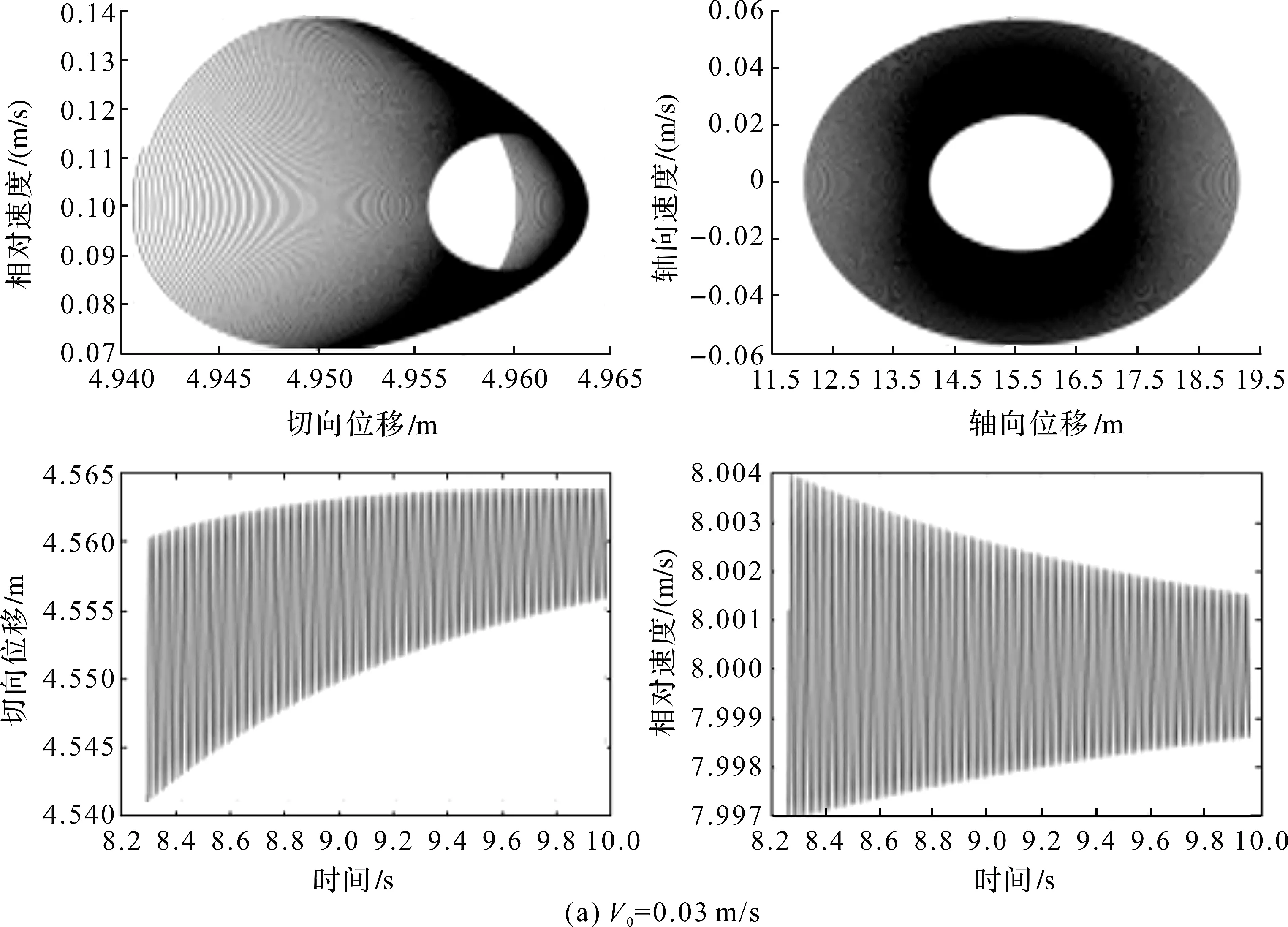
图4 不同初始速度下的相图、时域图

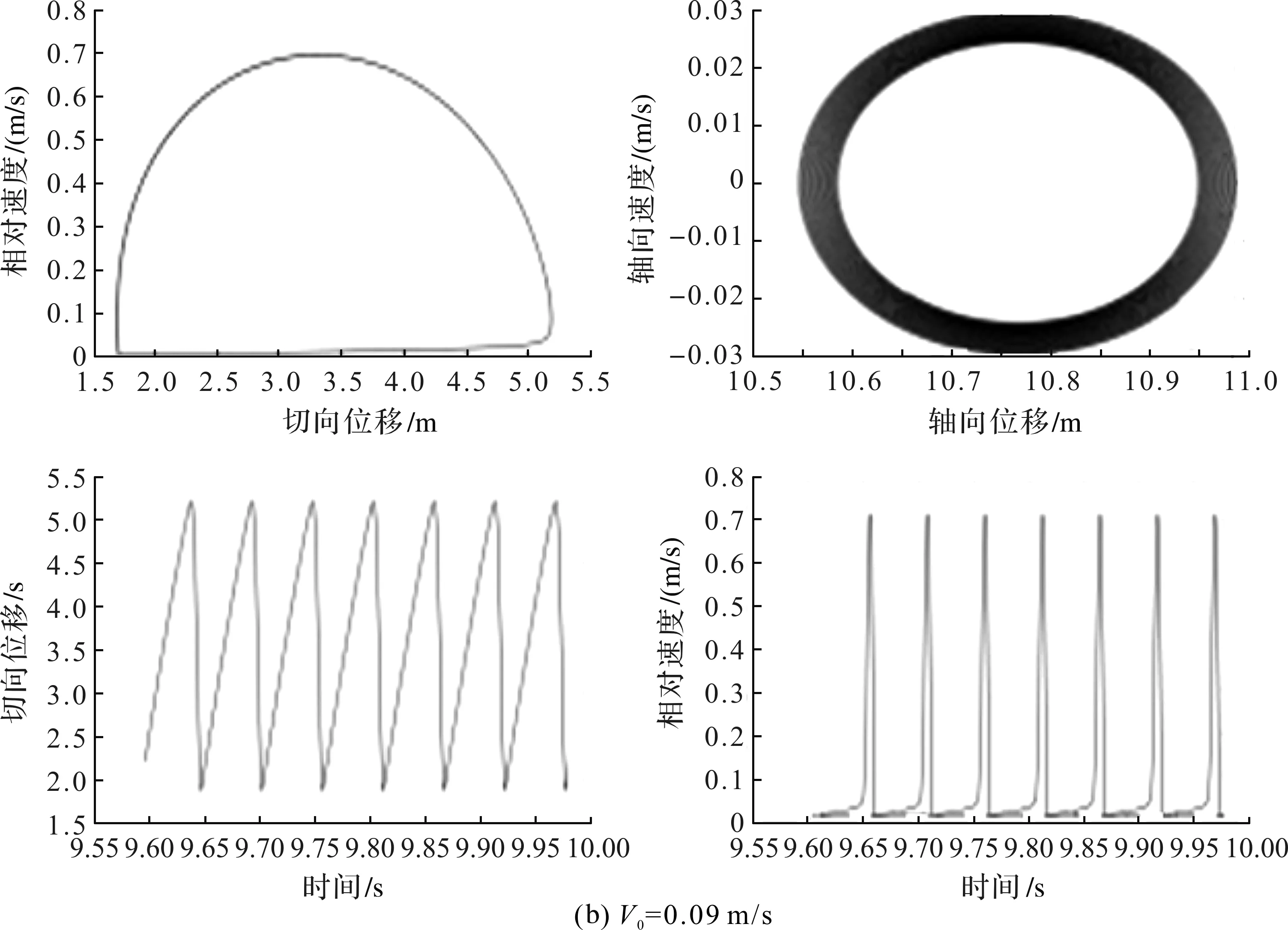
图4 不同初始速度下的相图、时域图(续1)

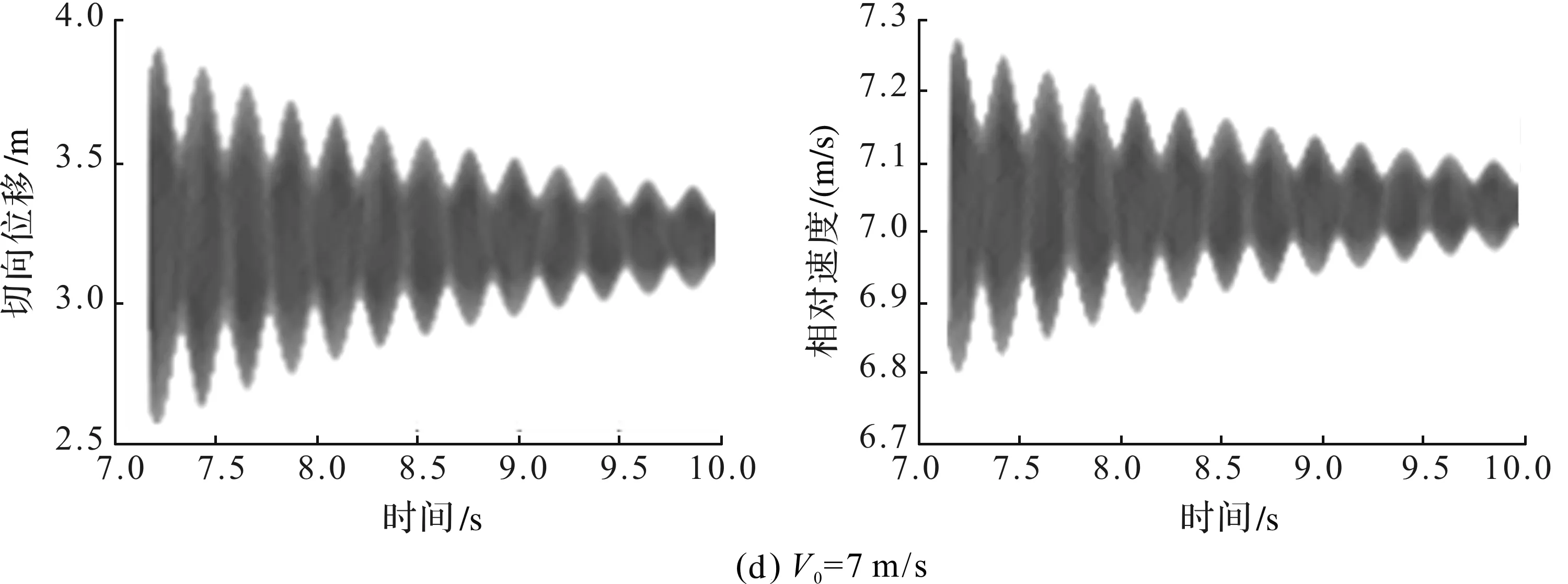
图4 不同初始速度下的相图、时域图(续2)

(1)当初始速度很低时(0.03 m/s),制动块做自激振动，并处于混沌状态，时域图具有明显的衰减趋势。

(2)初始速度增加到0.05 m/s时，制动块做多周期运动，具有明显的粘滑特性，每个小周期粘着时间为0.1 s。

(3)初始速度继续增加到0.09 m/s时，制动块由多周期运动转变为具有粘滑特性的单周期运动，粘着时间为0.05 s。

(4)随着初始速度的增加，系统很快又回到了多周期运动(0.11 m/s)，仍然具有明显的粘滑特性，每个小周期粘着时间变为0.3 s。

(5)当初始速度为0.15 m/s时，制动块运动又回到了单周期粘滑振动，粘着时间减少为0.25 s。

(6)随着初始速度的增加，系统又回到了多周期运动，直到进行周期不可分辨的混沌振动(0.6 m/s)，但此时粘滑特性也很明显。

(7)当初始速度足够大时(7 m/s)，制动块再次进入混沌的自激振动，并且不再具有粘滑特性。

4 结 论

本文通过引入具有指数形式的Stribeck干摩擦模型，建立包括切向和轴向两个自由度的制动系统力学模型，为研究干摩擦引起的非线性振动制动震动特性做了理论积累。通过不同制动压力、制动初速度下的相图与时域图分析，认为工作参数对制动系统的动力性能具有显著影响：(1)随着制动压力的不断增加，制动系统由最初的不具有粘滑特性的混沌自激振动转向具有粘滑振动特性的多周期自激振动，并最终走向单周期振动。在粘滑振动阶段，粘着持续时间越来越短，即振动频率在不断增加。(2)在不同的制动速度下，系统呈现了更为复杂的运动状况。随着制动速度的不断降低，系统由不具有粘滑特性的混沌自激振动走向单周期粘滑振动，然后走向混沌，后来系统状态在单周期与多周期粘滑振动之间来回转变，直到最后由多周期走向不具有粘滑特性的混沌自激振动。研究表明，干摩擦制动系统具有复杂的非线性动力学现象，而切向振动是导致制动颤振的主要原因，这为自动驾驶系统选择制动时机降低制动颤振和噪声提高舒适性提供了理论基础。