高层钢框架结构考虑P-Δ效应的弹性层间有害位移的简化计算*

皮凤梅， 任文杰， 陈博文， 赵 越

(1 河北工业大学土木与交通学院， 天津 300401；2 廊坊师范学院建筑工程学院， 廊坊 065000)

0 引言

高层钢框架结构自重轻、刚度小，在水平荷载作用下其变形相对较大。高层钢框架结构在水平荷载作用下的层间位移按对楼层是否直接产生受力变形通常分为两部分[1]：一部分是该楼层构件自身受力变形所产生的位移，包含梁、柱的局部弯曲变形产生的楼层剪切位移和本楼层框架柱轴向变形产生的楼层弯曲位移，称为层间有害位移所占的比例；另一部分是相邻下部楼层带动该楼层所产生的随动位移，属于框架柱轴向变形产生的楼层整体弯曲位移，该位移对本楼层的结构破坏不产生直接影响，称为层间无害位移。经研究发现[2]，层间有害位移在结构下部所占的比例很大，而越往上越小，在结构上部无害位移所占的比例大于有害位移。另外，在高层钢框架结构中，由于结构自身较柔，再加上重力荷载的存在使其在水平荷载作用下的侧移也随之增大，此时在侧移计算中把P-Δ效应考虑进去就显得尤为重要；而且，P-Δ效应产生的附加侧移中也同样会存在前述的层间有害位移和层间无害位移两部分。因此，目前的结构设计通常考虑的是楼层全部层间位移，未划分出层间无害位移，并不能真实准确地反映结构的实际受力变形情况。

目前，国外关于层间有害位移的计算鲜见于文献，而国内学者[3-6]虽提出了一些计算方法，但这些方法或是计算太过复杂不适合工程应用，或是略显粗糙，精度不满足要求。其中，翁大根等[5]基于有限元软件提出了刚度近似为零的斜向对角支撑法(简称对角撑法)，即：层间有害位移为ΔL/cosθ，ΔL为斜向对角杆件的伸长量，该值需借助有限元软件得到，θ为该杆件和水平杆件的夹角。该法虽然计算量较大，不便于工程应用，但可以清晰地反映出层间有害位移的概念，故可用于验证其它层间有害位移计算方法的可行性。此外，对高层钢框架结构考虑P-Δ效应影响的侧移计算，国内外学者已做了大量的研究工作[7-14]，提出了精确算法和近似的简化计算方法，一些方法也纳入了规范[15-17]，然而这些研究均没有在层间有害位移上做出进一步的剖析。

本文针对高层钢框架结构，从弹性阶段着手并考虑P-Δ效应，提出了层间有害位移的简化计算方法。以一个承受水平均布荷载的15层纯钢框架结构模型为例，分别采用对角撑法和简化方法计算比较结构的变形，以证明提出的简化方法的可行性，并讨论P-Δ效应对层间有害位移的影响。

1 一阶层间有害位移的简化计算

一阶层间有害位移的计算分为层间剪切位移和本楼层层间弯曲位移两部分。层间剪切位移直接按D值法[18，19]计算；本楼层层间弯曲位移分两步计算：先参照文献[18-19]计算层间整体弯曲位移，再按简化方法计算该层楼板转角，进而得到本楼层层间弯曲位移。

1.1 层间剪切位移

由D值法得到n层钢框架结构的第j层层间剪切位移，即：

(1)

1.2 层间整体弯曲位移与第j层楼板绕水平轴的转角θⅠj

图1 框架整体弯曲变形示意及计算简图

(2)

(3)

(4)

(5)

式中：MⅠ(z)为水平荷载在结构高度z处引起的弯矩总和，其表达式与外荷载的形式有关；B为两侧边柱轴线间的距离；s为边柱顶层与底层截面面积的比值，s=A顶/A底，其中A顶和A底分别为边柱的柱顶和柱底的截面面积。

整理得第j层整体弯曲层位移最终计算公式：

(6)

(7)

1.2.2 第j层楼板绕水平轴的转角θⅠj

(8)

1.3 层间有害位移

(9)

2 考虑P-Δ效应的附加层间有害位移的简化计算

目前，考虑P-Δ效应引起的附加层间位移的近似计算方法只考虑了附加层间剪切位移，没有包含附加层间整体弯曲位移这一部分。对此，我们做了进一步的研究，提出了高层钢框架结构考虑P-Δ效应的附加层间位移的简化计算公式，详见文献[20]。在此基础上，本节提出了附加层间有害位移的简化计算方法。

2.1 附加层间剪切位移

根据等效侧向荷载法[7]，假定各层特性与其他层无关，并将由P-Δ效应引起的柱内附加弯矩等效成该层的附加剪力所引起的效应，如图2所示。

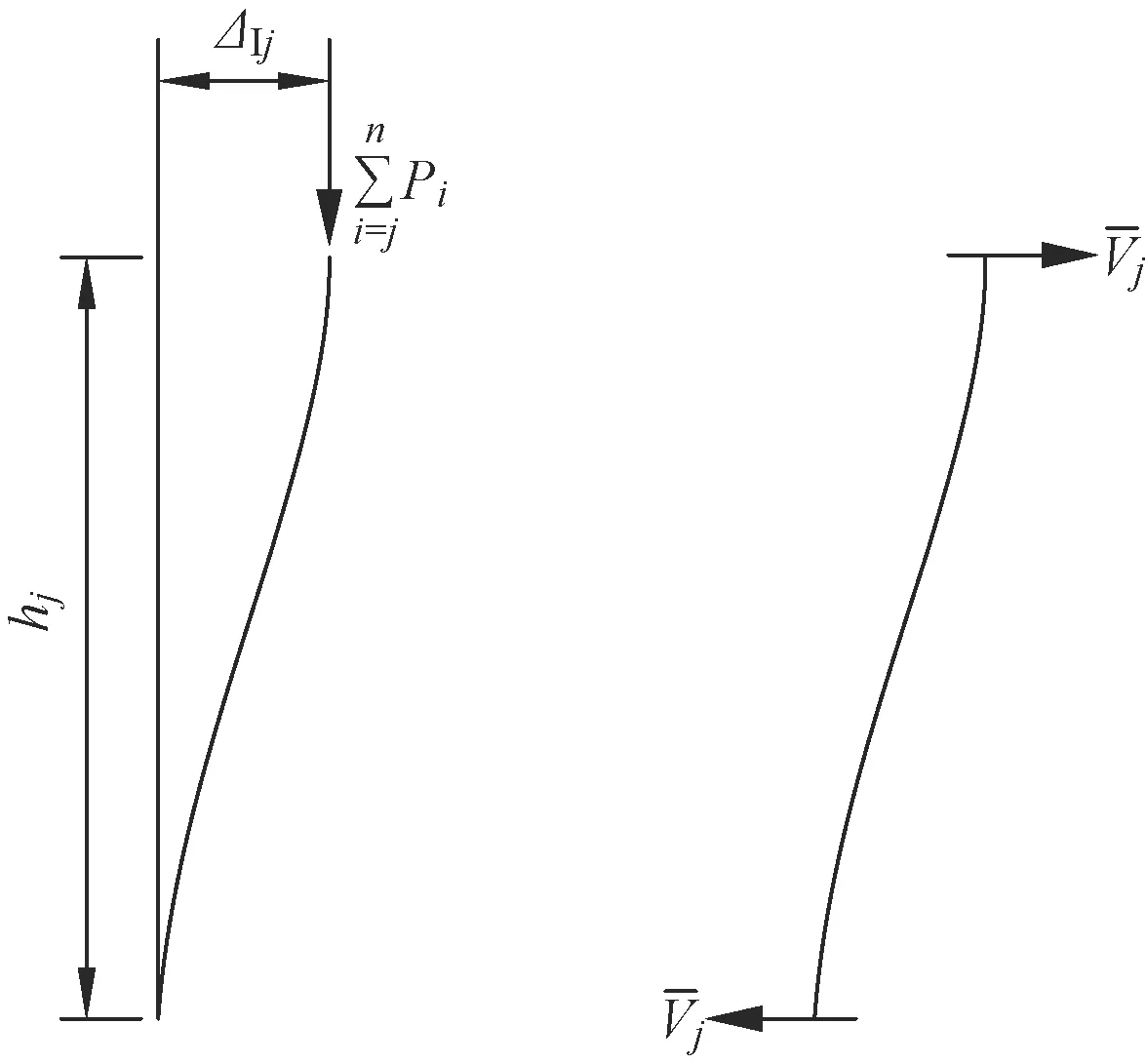
图2 等效附加层剪力

附加层剪力公式为：

(10)

(11)

2.2 附加层间整体弯曲位移

图3 附加层间整体弯曲位移的计算简图

重力荷载作用下，结构在高度z处产生的附加弯矩MⅡ(z)为：

(12)

2.3 附加层间有害位移

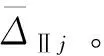
3 考虑P-Δ效应后的层间总位移及层间总有害位移

(13)

(14)

由于P-Δ效应引起的侧移具有随动附加性，因此需要将上述计算过程进行循环迭代，直到前后两次计算得到的层间有害位移近似相等，即可收敛。对于弹性阶段的计算通常只需要循环迭代1～2次就能够满足收敛要求。

4 数值分析

以一个承受水平均布荷载的单跨15层纯钢框架结构模型为例，考虑P-Δ效应，分别采用对角撑法和简化方法计算结构的层间总位移、层间总有害位移和层间总有害位移占层间总位移的百分比(简称层间总有害位移占比)，以评价所提简化方法的可行性，并通过一阶与二阶的层间有害位移的数据对比分析，讨论P-Δ效应对层间有害位移的影响。

4.1 计算模型

单跨15层纯钢框架结构模型计算简图如图4所示。两侧边柱间距离为6m，首层层高4.5m，其余层高均为3m，弹性模量E=2.06×105N/mm2，节点竖向集中力P=200kN，水平均布荷载q=10kN/m，框架柱截面采用H500×500×15×20，框架梁截面采用H500×200×10×16。

图4 单跨15层纯钢框架结构模型计算简图

4.2 结果分析

图5为简化方法(进行两次循环迭代收敛)与对角撑法的计算结果曲线图，表1列出了两种方法的层间总位移和层间总有害位移的相对误差。表2为简化方法下是否考虑P-Δ效应的层间有害位移对比情况。

图5 结构模型的位移曲线图

(1)从图5(a)可以看出，高层钢框架结构在水平荷载作用下，考虑P-Δ效应后，层间总位移从下到上先增大后减小，符合同时考虑剪切变形和整体弯曲变形的变形曲线特点。

(2)图5(a)，(b)表明，简化方法与对角撑法的层间总位移曲线吻合较好，两种方法算得的层间总有害位移也非常接近。表1也反映出它们的计算相对误差均不超过9%，能够满足工程精度要求，从而验证了本文提出的简化方法的可行性。

表1 简化方法与对角撑法计算结果的相对误差

(3)图5(c)中，随着结构楼层高度的增大，简化方法算得的层间总有害位移占比越来越小，并与对角撑法的结果很贴近，顶层层间总有害位移的占比不超过25%。这进一步说明，考虑P-Δ效应后，从有害位移的角度分析计算结构的二阶侧移，进行结构设计，能够更准确地反映结构的真实受力情况。

(4)从表2可以看出，结构的层间有害位移在考虑P-Δ效应后有所增大，且随着重力荷载的增加，层间有害位移值受P-Δ效应的影响加大，即P-Δ效应对层间有害位移的影响随楼层自上而下是逐渐增大的，最大增大率达到11.40%，不应忽略其影响。

表2 是否考虑P-Δ效应的层间有害位移对比

5 结论

(1)针对高层钢框架结构，从弹性阶段着手并考虑P-Δ效应的影响，提出了层间有害位移的简化计算方法。

(2)对一个承受水平均布荷载的15层纯钢框架结构模型进行了数值分析，通过简化方法计算得到的层间有害位移结果与基于有限元软件的对角撑法的计算结果吻合较好，能够满足工程精度要求。

(3)通过对简化计算方法得到的是否考虑P-Δ效应的层间有害位移的数据对比分析，得出P-Δ效应对层间有害位移的影响随楼层自上而下逐渐增大，最大增大率达到11.40%，故不能忽略其影响。

因此，本文提出的考虑P-Δ效应的层间有害位移的简化计算方法理论清晰明确，手算简便，易于编程，大大提高了计算效率，为实际工程的初步设计提供了一个可靠的参考。