基于SPSS的油液温度和闸门下滑量关系分析
彭杨金,文勇波,王显敏
(中国长江电力股份有限公司乌东德水力发电厂,云南 昆明 650000)
某电站进水口共设置12扇快速门,每扇快速门通过1台液压启闭机进行启闭。进水口快速门液压启闭机是引水发电系统中重要的保护设备之一,对机组的安全运行起着非常关键的作用。当水轮机组发生飞逸或压力钢管发生破裂事故时,闸门快速关闭进水口,切断水流,达到保护机组和防止事故继续扩大的目的[1-2]。
在对快速门液压启闭机进行巡检的过程中,记录闸门开度、油液温度、闸门下滑量等数据是必不可少的工作之一。通过巡检记录的数据发现,液压系统正常条件下,油液温度和闸门下滑量之间存在一定的关系。为增强运维人员对液压启闭机设备性能的掌握,本文运用SPSS统计软件对某台液压启闭机设备巡检记录的数据进行分析。
1 SPSS概述及回归模型的建立
1.1 SPSS软件概述
SPSS社会科学统计软件包是世界最著名的统计分析软件之一,该软件包的内容覆盖了从描述统计、探索性数据分析到多元分析的几乎所有统计分析功能;SPSS的基本功能包括数据管理、统计分析、图表分析、输出管理等;SPSS统计分析过程包括描述性统计、均值比较、一般线性模型、相关分析、回归分析、对数线性模型、聚类分析、数据简化、生存分析、时间序列分析、多重响应等几大类[3]。
SPSS统计软件操作简单方便,有多种数据交换的格式,能很好地与其他软件进行交互,使用的统计方法先进成熟,被广泛应用在自然科学、经济管理等各个方面。
1.2 数据来源及模型建立
分析所用数据来源于2010年7~10月乌东德电站某台进水口快速门液压启闭机巡检记录,选取了其中的油液温度和闸门下滑量数据,见表1。
线性回归分析是基于最小二乘法原理产生的古典统计假设下的统计分析方法,用来研究一个或多个自变量与一个因变量之间是否存在某种线性关系[4]。只有一个自变量时,是一元线性回归,又称简单线性回归;有两个及以上自变量时,称为多元线性回归。本文采用的是一元线性回归分析,将油液温度设为自变量X,闸门下滑量设为因变量Y,建立回归模型,其中ε为其他因素误差。
Y=β0+β1X+ε
(1)
线性回归的拟合程度为判定系数R方,回归方程和回归系数的验证分别为F和t显著性检验[5]。
2 基于SPSS的线性回归分析
将巡检数据导入SPSS统计软件进行回归分析,分析的结果见表2~表5以及图1和图2。表2是模型汇总表,给出了评价模型的检验统计量,相关系数R为0.882,R方为0.778,调整后的R方为0.767,说明回归的拟合程度较高。
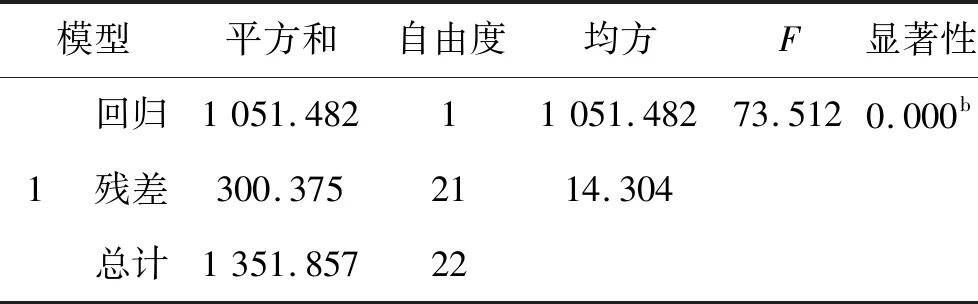
表3 方差分析表
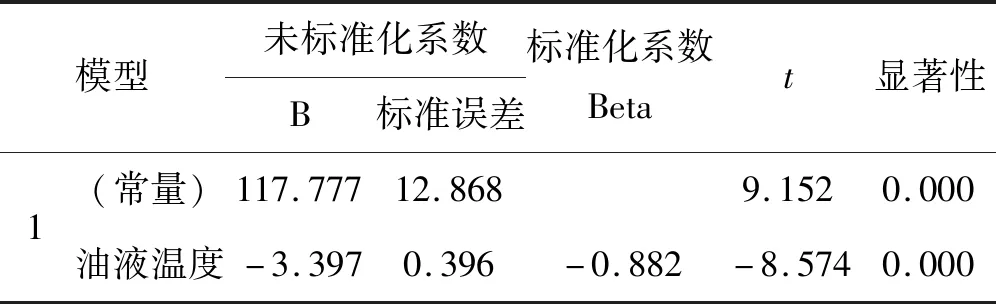
表4 回归系数分析表
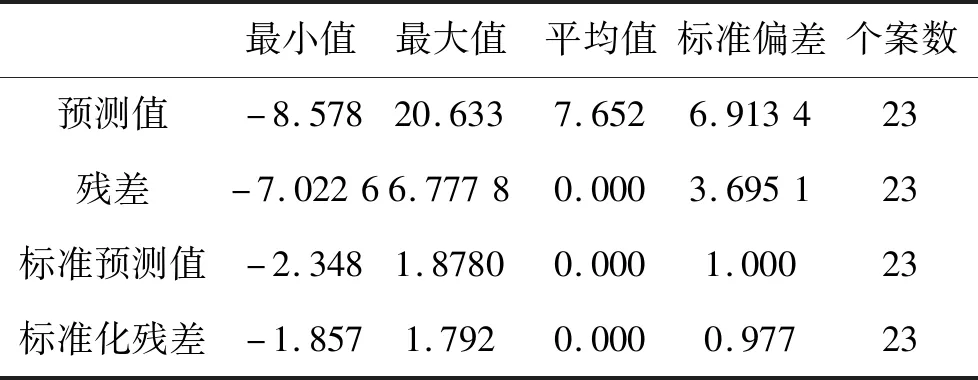
表5 残差统计表
表3中给出了方差分析的结果,由该表可知,回归平方和为1 051.482,残差平方和为300.375,自由度分别为1和21,回归均方为1 051.482,残差均方为14.304,回归方程的显著性检验统计量F=73.512,相应的显著性值为0.000,小于显著水平0.05,因此可以判断由液压启闭机油液温度对闸门下滑量解释的部分非常显著,所建立的回归模型具有统计学意义。
表4是回归系数分析表,其中给出了线性回归模型的回归系数及相应的一些统计量。由该表可得到线性回归模型中的常数为117.777,自变量油液温度的系数为-3.397,常数的t值为9.152,油液温度的t值为-8.574,相应的显著性值为0.000,小于0.05,说明系数非常显著,因此所建立的回归方程为
Y=117.777-3.397X
(2)
表5中给出了一些残差的统计量,从该表中能够得到预测值、残差、标准预测值和标准残差的最小值、最大值、平均值等统计量。其中标准化残差的绝对值最大值为1.857,没有超过默认值3,显示结果无异常现象[4]。
图1为标准化残差的直方图,从该图中可以看出标准化残差分布服从正态分布。图2为标准化残差的累积概率图,该图以实际观察值的累积概率为横轴,以正态分布的累积概率为纵轴,如果样本数据服从正态分布,则所有散点都应该分布在对角线附近[6]。从图中可看出散点确实都在对角线附近,因此可以认定标准化残差分布服从正态分布。
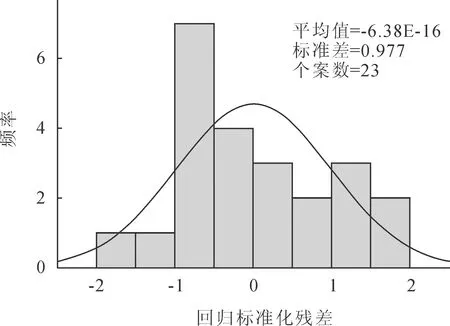
图1 标准化残差的直方图
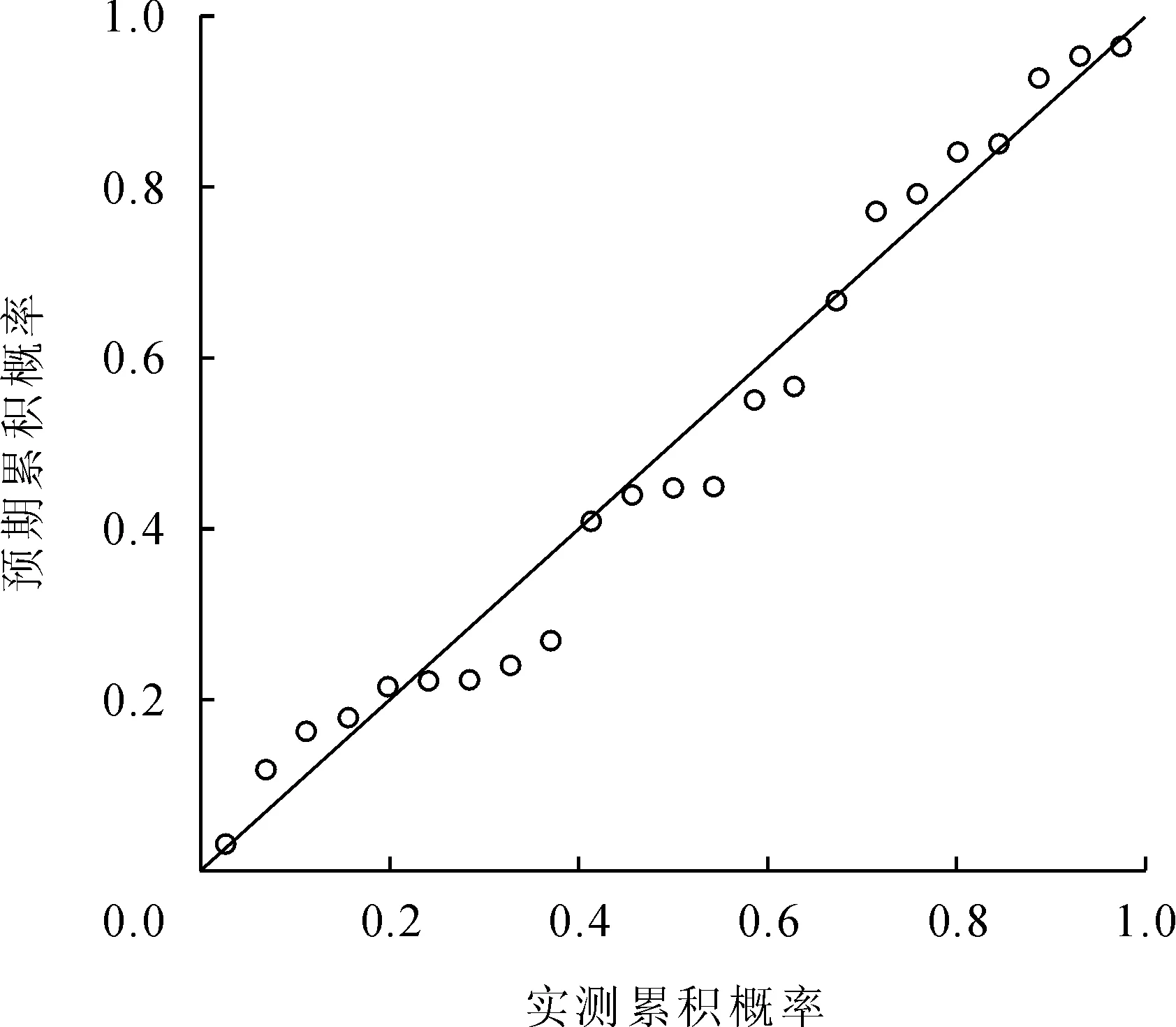
图2 标准化残差的累积概率图
3 结 语
通过SPSS统计软件对某电站某台进水口快速门液压启闭机巡检记录数据进行分析,得出其油液温度和闸门下滑量之间存在高度的线性关系,并得出了线性回归方程:Y=117.777-3.397X,这对运维人员全面了解设备性能有较好的参考借鉴作用,有利于设备的安全运行及维护,也为机组的安全稳定运行提供了保障。

