风流模型在不同地形上的使用研究
张 静,杨靖文,王先阳
(北京瑞科同创能源科技有限公司,北京 100079)
在风资源评估工作中,风流模型的重要性是不言而喻的。掌握准确而详细的风资源分布是合理的风电场设计及准确的发电量估算的基础。
早期如WAsP这类线性风流模型被广泛应用。它的特点是占用的计算资源比较少,而且在地形条件并不十分复杂的情况下,运行速度也很快,可用于推算平均风速、风向、风频、风切变以及其他特征的空间变化[1-2]。
质量守恒模型则通过初始观测数据来构建初始稳态风场,使用定义在三维网络上的三个变量的增量,进行迭代计算网格点上的变化直至收敛[3]。在假定同一海拔高度的大气密度恒定的条件下,求解质量守恒方程。
计算流体动力学(CFD)是目前逐渐替代线性模型成为主导风能应用的新一代的风流模型。大多数CFD模型求解是非线性的Navier Stokes方程的质量和动量守恒方程,并运行至常态风廓线进行收敛[4]。
本文使用了上述风流模型,借鉴Philippe等(2012年)的实验方法,对几种典型地形的站点风资源进行了模拟,旨在研究各风流模型的计算差别以及对地形的适应性。
1 风流模型分析
1.1 线性模型-WAsP
大多数线性模型都是基于Jackson-Hunt理论模型。Jackson-Hunt(1975年)提出Navier-Stokes方程的线性化模型[5]。
该模型是根据傅立叶分量分析地形形状(扰动),并要求扰动的水平尺度要远小于边界层显著变化所需的距离(小扰动理论)。用风能资源评估的话,这也意味着项目区域必须处于相同的风气候下[5]。
Mason和Sykes(1979年)将Jackson-Hunt模型扩展到三个维度,并通过采用置换法开发了MS3DJH(Jackson-Hunt理论三维扩展)代码。在这种方法中,引入了波数定标技术的概念,以解决实际地形水平标度的大范围问题,而不仅仅是Jackson-Hunt模型中的水平标度范围。在MS3DJH中,由表面粗糙度引起的扰动与由高度变化引起的扰动是线性叠加的[6]。
而后丹麦Risø国家实验实验室在Jackson-Hunt理论的基础上,基于MS3DJH模型开发了WAsP(Wind Atlas Analysis and Application Program)。该模型在以下几个假设下求解线性化的Navier-Stokes方程:稳态流,线性对流和一阶湍封闭。此外,仅将地形作为一阶扰动考虑在内。
WAsP模型简单易用且需求较少的计算资源,并且具有很高的可重复性,即不同的用户只要使同相同的输入,很容易得到相似的结果。
1.2 质量守恒模型-WindMap/Openwind
质量守恒模型是从一组没有时间相关项的初始实验数据重建稳态风场,来模拟平均风速,是从观测数据构建质量一致的风场。因为它仅求解一个控制运动方程,即质量守恒,因此不需要大量的计算资源。
大多数质量守恒模型基于NOABL代码[6],例如MATHEW,MINERVE,COMPLEX,WINDS等。与其他质量守恒模型一样,WindMap/Openwind模型也基于NOABL代码,考虑了由于急剧的表面粗糙度变化而引起的内部边界层的增长。
这些模型在风资源评估应用中没有像在商业气象和环境研究中那样广泛地用于商业领域,可能是因为它们与WAsP具有相似的局限性,并且其结果通常表现出与WAsP的相似性。
对于质量守恒模型一般的共识是,与WAsP相比,它们在模拟复杂地形中的静态三维风场方面具有更好的仿真能力。质量守恒模型在很大程度上受限于对地形模拟的效果。因此,质量守恒模型也可以使用其他风流模型的结果作为输入数据,比如与中尺度模型进行耦合,使用中尺度模型计算的风资源图作为输入数据,然后在复杂的地形中实践质量守恒的模型,以改善首次猜测并获得更好的风资源评估结果[7]。
WindMap模型使用预置的默认配置和可修改的自定义设置平稳了用户间不同的需求。专业度较低的用户可以选择使用预置的默认配置,而专业度较高的用户则可以对参数进行自定义的修改以便更精细的进行模拟风场。
1.3 CFD模型-Meteodyn WT
计算流体动力学(CFD)拥有属于其自己的专业学科。所有CFD模型本质上都是RANS方程求解器,即同样是基于Navier-Stokes方程。与的Jackson-Hunt模型相比,求解了更为完整的RANS方程,既没有线性化,也不需要附加流体和一阶封闭等假设,并且可以进行小范围扰动。故而CFD模型的巨大优势在于,从理论上讲,它们能够模拟非线性流动现象,例如流动分离和再循环,也就是说CFD模型在模拟地表风时,可以很好应对地表风中存在的一些非线性的影响。这一优势在复杂的地形站点或存在障碍物或森林的地方更为明显。而且CFD模型还可以模拟整个地形的影响,并不会像WAsP一样依赖于单独的模块。
CFD模型具有更广泛的适用性。通用CFD软件,例如PHOENICS,CFX,FLUENT,OpenFOAM和STAR CCM+,适用于稳定或不稳定,一维、二维或三维湍流或层流,可压缩或不可压缩流体,粘性或无粘性流体,并且具有更多更灵活的网格划分选项。
与Jackson-Hunt模型和质量守恒模型不同,CFD模型主要求解RANS和连续性方程,因此无法解决关于大气稳定性和热诱发环流的热条件,这导致了诸如中性分层大气的假设(可以通过简单的参数,例如热通量或湍流尺度等进行调整)和对数定律的垂直风廓线以及规定的平衡入流条件,尽管受限于可用的计算资源,但通常也假定为稳态流。
不过,使用CFD软件为风流进行建模,需要使用者拥有广泛的专业知识,才能很好地对模型各参数进行设置。其次,由于CFD模型通常需求大量的计算资源,从而增加了硬件成本。而且,CFD模型的计算结果通常很大程度上取决于使用者的经验,这对于风资源评估来说具有非常不可控的不确定性因素,因为这意味着结果也很难被其他对同一项目进行评估的人重复,从而降低了项目的可重复性与可验证性。
2 研究方法
2.1 项目选择
选择平原项目、山地项目及丘陵项目,如图1~图3所示,每个项目具有至少3个以上的测风站点,并且站点具有同期1年的同高度的测风数据。测风站点基本信息见表1。

表1 测风站点基本信息表
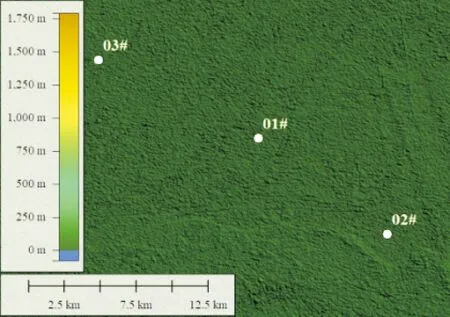
图1 平原测风站点位置示意图
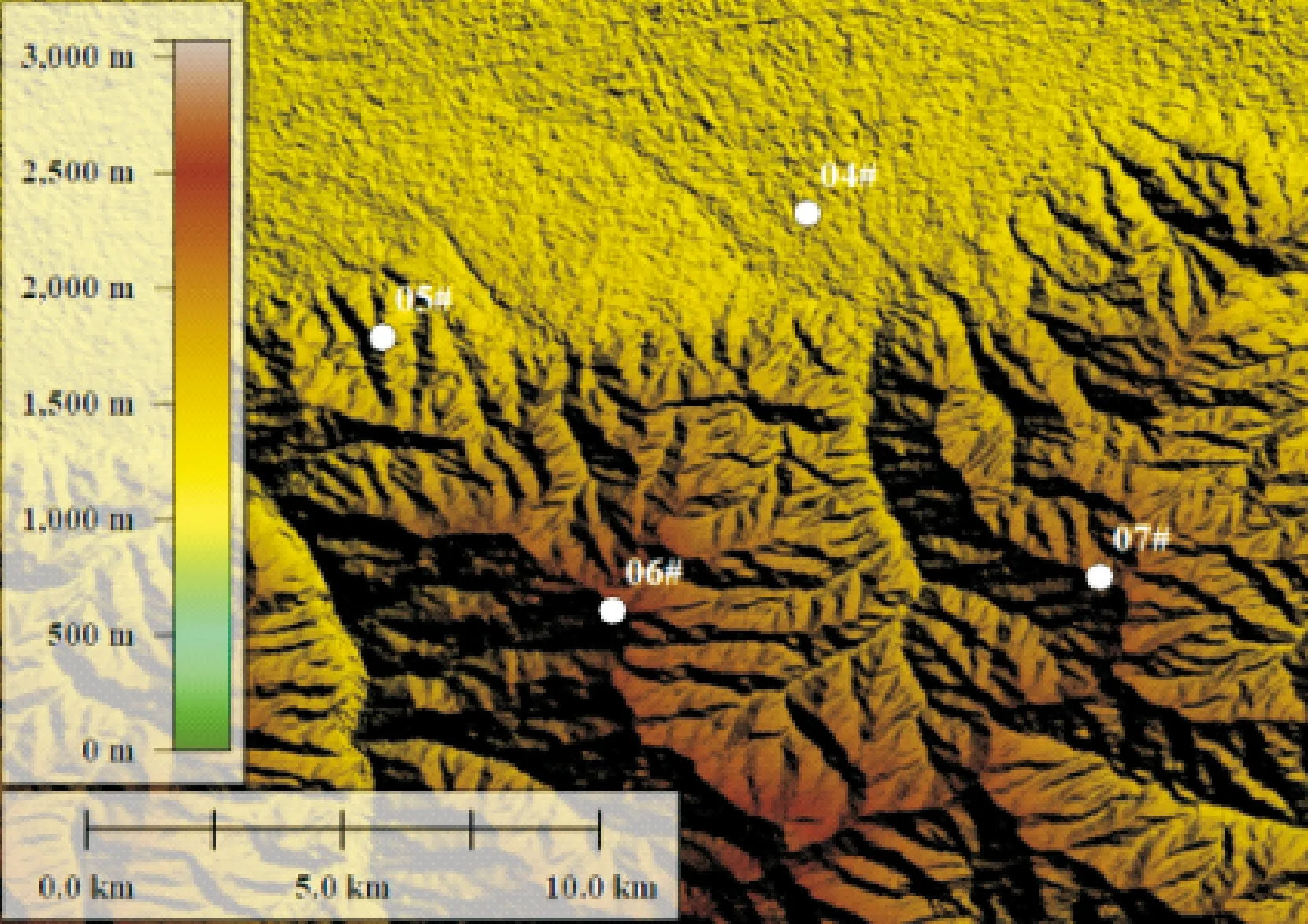
图2 山地测风站点示意图
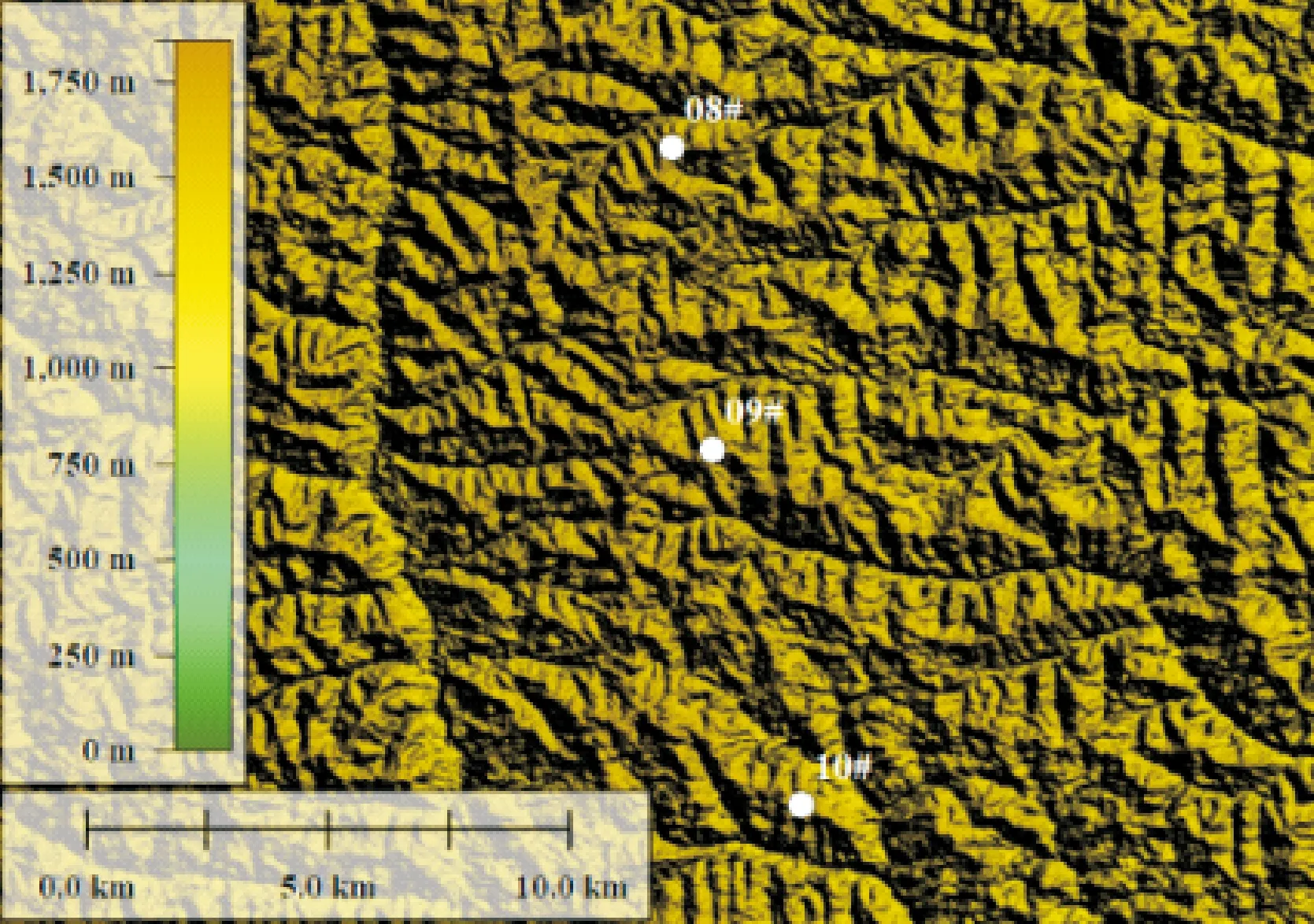
图3 丘陵站点位置示意图
2.2 方案设置
对每个项目,每次使用其中一个测风塔对其他测风塔站点位置的风速进行推算,各风流模型使用相同的输入条件,即测风数据、地形数据、地表粗糙度数据完全一致,并且各风流模型的分辨率均设置为30 m。
2.3 误差指标
每个站点的误差度量是预测和观察到的平均风速之间的均值偏差、平均绝对误差(MAE)、均方根误差(RMSE),定义如下:
(1)
(2)
(3)
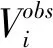
3 结果分析
通过使用线性模型WAsP/WindPRO,质量守恒模型WindMap/Openwind,以及CFD/Meteodyn WT三种不同的风流模型,对所选区域测风站点进行交叉预测,将得到的结果汇总形成表2、表3以及图4~图6。
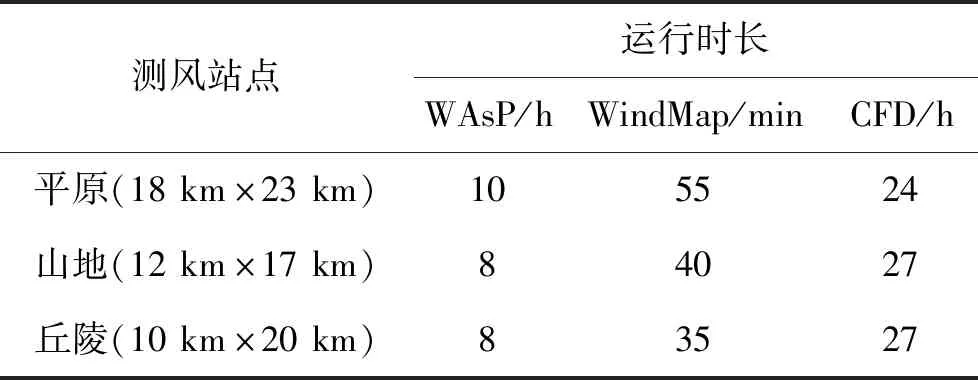
表2 风流模型计算30 m分辨率风资源网格用时
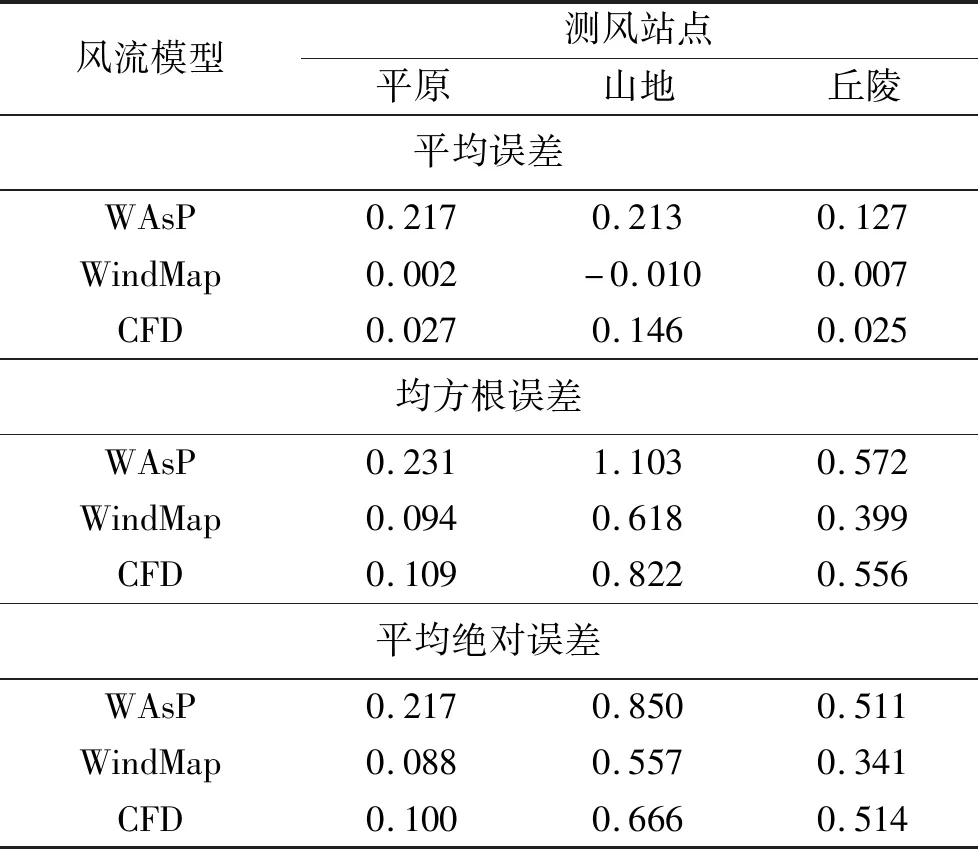
表3 各区域误差统计 m/s
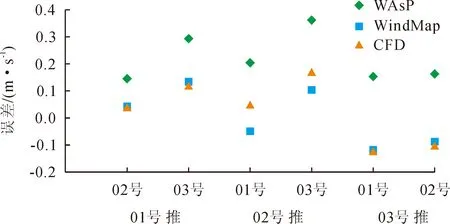
图4 平原站点交叉预测误差
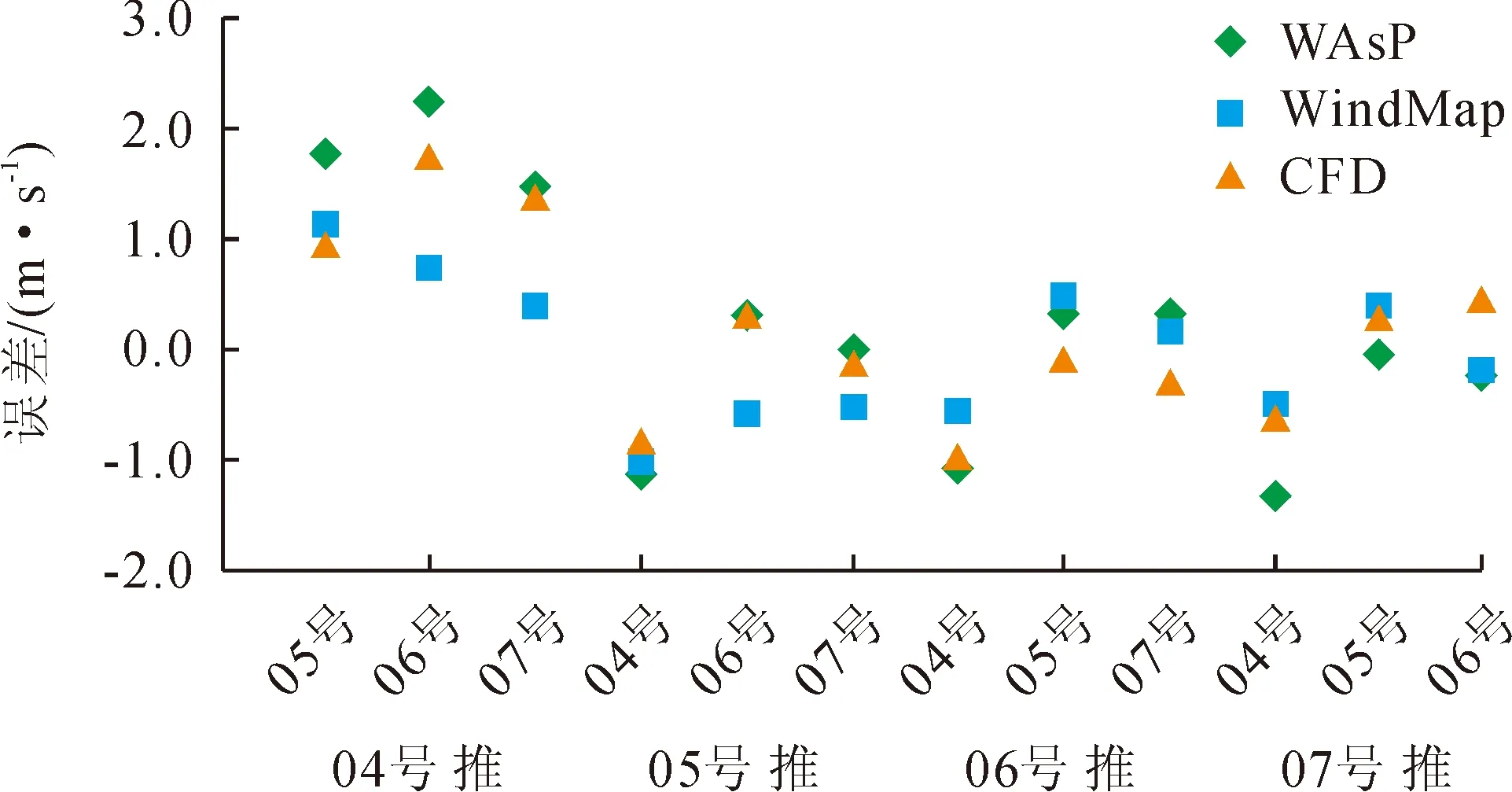
图5 山地站点交叉预测误差

图6 丘陵站点交叉预测误差
通过对以上结果进行分析可以得出:
1)每一个测风数据所得到的一组预测数据,预测值的大小与使用的实测数据整体趋同;即表明,使用高风速站点的测风数据去推测低风速站点的风速值,所得预测值偏高,反之,使用低风速站点的测风数据去推测高风速站点的风速值,所得预测值也偏低。
2)平原区域的站点在进行交叉预测时,各风流模型表现都比较好,线性模型对风速的预测误差较质量守恒模型与CFD的误差要高2%~3%。
3)山地及丘陵站点的交叉预测误差相较于平原站点交叉预测的误差明显偏高,各风流模型的准确度均受限于地形影响。但是横向对比可以看到,质量守恒模型以及CFD模型在处理复杂地形上,比线性模型具有更好的适用性。
4)质量守恒模型由于只求解一个质量守恒方程,且可以进行多线程计算,故而其计算资源较线性模型和CFD模型更少,运行速度更快。
4 结 语
文中以3个不同地形区域,10个测风站点,进行了10次交叉预测,从结果分析得出质量守恒模型以及CFD模型较线性模型有更好的适应性,质量守恒模型由于只求解一个质量守恒方程,在计算资源的需求上较另二者更低,更具有便捷性。
文中所涉及的三种地形都仅使用一个项目作为代表进行实验,故而结果并不具有科学的广泛适用性,有必要进一步扩大案例研究的样本,扩大其代表性。

