基于BIM的铁路车辆-无砟轨道护轨性能分析

刘沛 陈卫国 张耀

中铁二院工程集团有限责任公司，成都610031

建筑信息模型（Building Information Modeling，BIM）技术在铁路工程设计领域发展迅速，各专业正逐步实现完全或部分BIM正向设计。伴随设计环境与设计内容的三维化进程，对设计方案性能的校核分析工作也应实现空间可视化。基于BIM平台和BIM模型在三维环境中直接对设计模型开展三维仿真计算分析是当代轨道交通领域数字化设计阶段的关键手段之一［1］。

目前国内外多用刚体动力学理论分析脱轨后无砟轨道的护轨性能，忽略了车辆与钢轨的柔性变形和轨道板自身的挠度，导致仿真结果与实际运动状态相差较大［2-3］。从有限元角度出发，将BIM模型离散为全尺寸有限元模型，可以降低仿真模型与实际状态的差异。利用动态非线性有限元方法解决运动和变形问题，可以使列车在脱轨后撞击轨枕块及护轨过程中的传力过程和运动状态具有真实的柔性体本质，从而提高铁路工程BIM三维设计的效率和准确性［4-5］。

本文选取某高速铁路双块式双线直线无砟轨道护轨段BIM设计模型为研究对象，以某市域列车头车车辆作为脱轨车辆来分析护轨的防护性能，通过创建基于BIM模型的无砟轨道-车辆有限元脱轨分析模型，设置基于欧洲标准EN 15227—2020《Railway Applications—Crashworthiness Requirements for Rail Vehicles》［4］和国内外列车脱轨事故［5］的脱轨场景和边界条件，利用LS⁃DYNA软件对该护轨结构的防护性能和设置方案进行仿真，研究轨道的护轨结构对车辆的保护作用和自身的力学响应。

1 脱轨分析理论

车辆在脱轨后与轨道结构发生碰撞，通过钢轨和车辆自身的变形及两者之间的摩擦来消耗动能。为了更真实地模拟车辆与轨道碰撞时的柔性特征，以动态非线性大变形有限元理论作为脱轨分析的理论基础。

1.1 动态非线性有限元基本方程

基于宏观的运动学和微观的弹塑性变形原理，车辆的脱轨与护轨碰撞过程的任意质点须满足运动方程、连续性方程、动量守恒方程、能量守恒方程以及各类边界条件（面力边界、位移边界、接触边界），并最终满足以下平衡方程［6］：

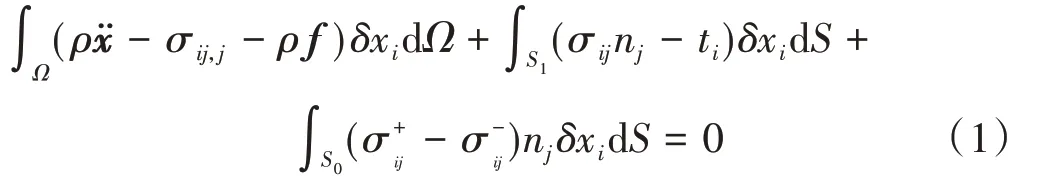
式中：Ω为空间域；ρ为质量密度；ẍ为质点加速度；σij为应力张量，向j求导即为σij，j；f为单位质量所受体积力；xi为质点在任意时刻ti的位置坐标，δxi表示位移微量；S1、S0分别为面力边界、接触边界；nj为表面外法线方向单位向量；分别为接触边界两侧对边界上产生的应力。

1.2 积分算法

求解运动方程多采用显式中心差分法，其为预测性质的递推方法。LS⁃DYNA软件采用的是一种计算精度较高的中心差分法的变异表达，求解时位移、速度、加速度在不同的时刻交错，因此被称为“蛙跳式中心差分法”［7］，其表达式为

式中：M为总体质量矩阵；P为由节点载荷、面力和体积力组成的总体节点载荷向量；F为单元应力场集成的等效节点载荷向量；H为每个单元节点处的沙漏阻尼力集成向量；C为总体阻尼矩阵；ẋ为质点速度，x为质点位移；t的下标表示不同的时刻；Δtn、Δtn+1分别为tn、tn+1时刻的时间步长。

根据式（2）—式（4）可得到tn+1时刻的位移x(tn+1)，加上初始构型便可得当前构型。

2 无砟轨道-车辆模型

2.1 无砟轨道模型

2.1.1 无砟轨道BIM正向设计流程（图1）［8］

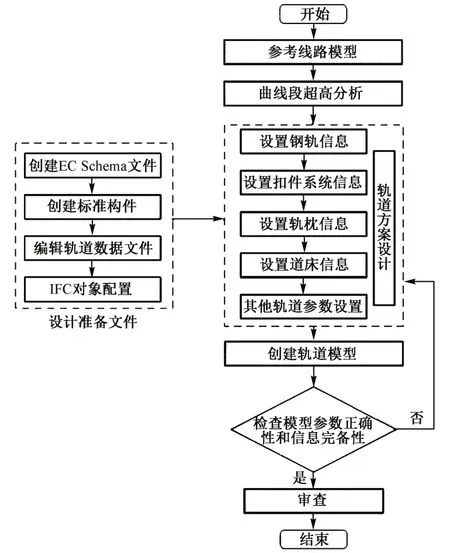
图1 轨道BIM正向设计流程

设计前先依照IFC/IFD编码标准创建EC Schema文件，用建库工具创建轨道标准构件及模板，整理好钢轨、轨枕、道床等部件的布置和规格信息文件。开始轨道设计时，通过协同设计平台参考路线模型，分析曲线段超高，导入钢轨、轨枕、道床等部件的相关数据文件，交互编辑超高信息，然后生成轨道设计方案。基于此设计方案，生成轨道三维BIM模型，然后检查模型参数的正确性和信息的完备性直至符合设计技术要求。

2.1.2 创建无砟轨道“BIM+有限元”模型

选取某高速铁路双块式双线直线无砟轨道护轨段为研究对象。该路段全长45 m，左右线线路中心距4.4 m。护轨与外侧钢轨安装在同一轨枕块上，与运行轨间距0.330 m；内侧钢轨不设置护轨，轨枕块纵向间距0.625 m；护轨与运行轨顶面高程相等。护轮轨道设计如图2所示。

图2 护轮轨道设计方案示意（单位：mm）

根据上述设计方案，利用基于Bentley⁃OpenRail Designer软件二次开发的铁路轨道三维正向设计工具，通过超高分析、计算轨道配板及布设参数，设计并创建出该路段LOD3.0等级的轨道BIM模型，包括轨道板、轨枕块、钢轨、扣件、钢轨垫板、扣件螺栓等，如图3所示［9-10］。

图3 双块式无砟轨道护轨段BIM模型及主要构件细节

根据有限元理论的网格划分原则，采用HyperMesh14.0软件把整个双线轨道的BIM模型离散成具有真实的构件间连接和接触关系的有限元模型［11］。其中，将轨道板、轨枕块、钢轨、钢轨垫板、扣件螺栓离散成8节点的实体单元，扣件弹簧用3节点梁单元模拟，并设置预紧力。双块式双线无砟轨道有限元模型共有641 253个单元。

2.2 车辆模型

选取某市域列车头车车辆作为脱轨车辆来分析护轨的防护性能。为使脱轨仿真结果具备更真实的脱轨形态和力学变化过程，须创建准确而合理的车辆有限元模型，主要包括车辆转向架与车体结构。

转向架作为车辆的独立部件，是脱轨分析过程中传递轮轨作用力的唯一部件。利用HyperMesh14.0软件将车辆主体结构离散为24 561个4节点薄壳单元和1 897个8节点实体单元，一系、二系空气弹簧分别用36、72个6自由度的离散梁单元模拟，枕梁与车体之间的连接关系用点焊模拟。转向架有限元模型如图4所示。根据LS⁃DYNA的关键字手册［12］，将模型薄壳单元的积分算法设置为Belytschko⁃Tsay法，实体单元为CSSE法，离散梁单元为discrete beam法。

图4 市域列车头车转向架有限元模型

该车辆车体为铝合金结构。首先将车辆三维模型中面化，并确保正确的组件连接关系，然后将车体三维中面模型离散成由875 903个薄壳单元组成的有限元模型，用Mass21单元搭配Beam单元模拟车内安装的各类设备，通过节点耦合的方式将二系弹簧与车体进行连接。

2.3 无砟轨道-车辆模型

车辆在脱轨时对处于运行轨道旁边的护轨有一定的冲击作用，护轨结构对脱轨列车起保护作用，综合护轨轨道和车辆的有限元模型形成脱轨系统。脱轨系统质量为54.165 t，车轮与轨道之间设置防止互相穿透的面面接触，车辆自身设置防止自身构件互相穿透的单面接触。最终建立的脱轨系统有限元分析模型如图5所示。

图5 脱轨系统有限元分析模型

3 车辆脱轨仿真计算及结果分析

根据列车的运行特征，对列车模型施加横向和纵向平动初始速度作为动能输入条件，依据文献［4-5］确定计算工况的边界条件，见表1。

表1 车辆脱轨边界条件

利用LS⁃DYNA求解器的显式求解算法对脱轨系统进行计算。为了保证模型系统在计算时顺利进行，除了设置上述边界条件外，还须将积分时间步长设为10-6s，分析终止时间设为200 s，文件输出时间间隔设为10-3s；为了得到更好的输出结果内容与形式，设置二进制输出文件控制卡片（DATABASE_OPTION），主要的输出控制参数包括DEFORC、ELOUT、GLSTAT、MATSUM、NODFOR、NODOUT、RCFORC、SLEOUT、SPCFORC、SWFORC、BINARY_D3PLOT。针 对LS⁃DYNA计算结果和所设置的输出数据进行相应的数据滤波处理，得到各主要指标的分析结果。

3.1 脱轨过程形态变化

车辆在脱轨过程中与轨道的主要形态变化如图6所示。可知：脱轨前，车轮与钢轨之间保持正常的轮轨接触关系［13］；车辆脱轨时，护轨侧车轮首先从运行轨掉落，同时远离护轨侧的车轮爬上运行轨道，被爬钢轨发生横向弯曲；爬轨轮越过钢轨后，两侧车轮同时向下掉落至轨道板及轨枕块，车轮在纵向运行的同时继续横向靠近护轨；护轨侧车轮与护轨发生接触后，护轨阻止车轮继续横向移动，护轨出现横向弯曲，车轮从轨枕块掉至轨道板，致使车辆发生倾斜但未倾覆，最终车辆以倾斜但未倾覆的稳态与护轨摩擦向前滑行。

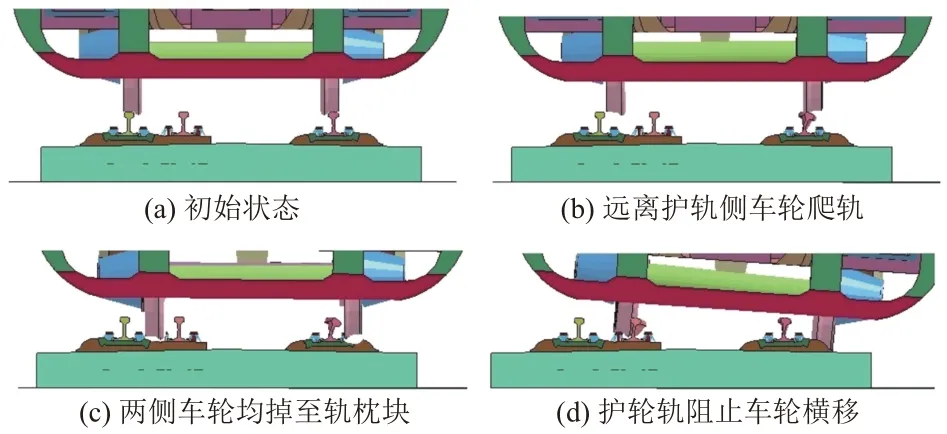
图6 车辆脱轨过程形态变化

3.2 能量变化

车辆运行的动能决定了脱轨后车辆对护轨的冲击破坏程度［14］。脱轨过程中车辆的动能变化见图7。可知：在0～0.05 s系统发生了第一次动能稳定下降，此过程为爬轨侧车轮与钢轨碰撞摩擦吸能；在0.12 s之后动能稳定下降，此时为护轨侧车轮与护轨碰撞摩擦吸能，之后的动能均以摩擦热的形式耗散。

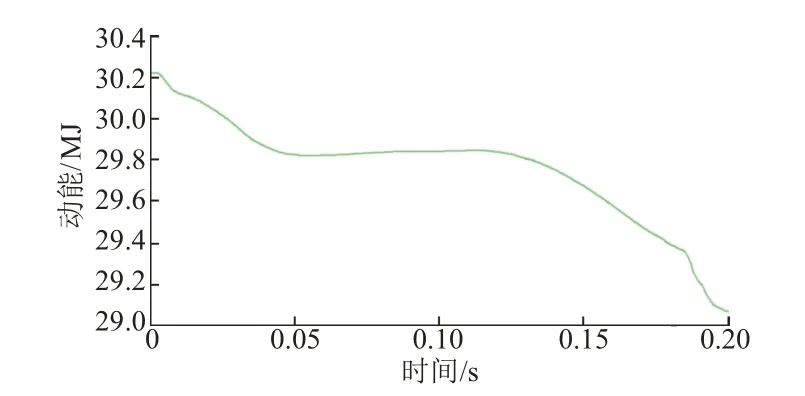
图7 脱轨动能随时间变化曲线

3.3 轮轨接触力

车辆脱轨后轮轨接触力大小决定了钢轨给予车辆的横向冲击加速度大小，从而决定了护轨对车内乘客与设备的横向冲击程度［15］。轮轨接触力随时间变化曲线见图8。可知：在0.008～0.052 s，爬轨侧车轮与钢轨接触造成了轮轨间第一次横向冲击，x、y、z方向的冲击力峰值分别为540、1 000、2 750 kN；0.052 s后爬轨侧车轮从钢轨上脱落，整个转向架在重力作用下横向空行；在0.105 s时护轨侧车轮与护轨接触造成第二次轮轨冲击，x、y、z方向的冲击力峰值分别为352、1 500、300 kN。

图8 轮轨接触力随时间变化曲线

3.4 轮对抬升量

轮对抬升量决定了车辆脱轨后的危害程度。轮对抬升量（垂向位移）越大，脱轨后的危害程度越大［16］。轮对抬升量随时间变化曲线见图9。可知：脱轨过程中，爬轨侧车轮与钢轨发生碰撞后，在巨大的横向压力与动能作用下，轮缘爬过钢轨，发生较大的垂向位移，爬至轨顶时车轮的垂向位移达到最大值，为17.622 mm；同时护轨侧车轮垂向位移也达到最大值，为5.540 mm。爬轨侧和护轨侧车轮垂向位移均满足车辆运行安全性要求。

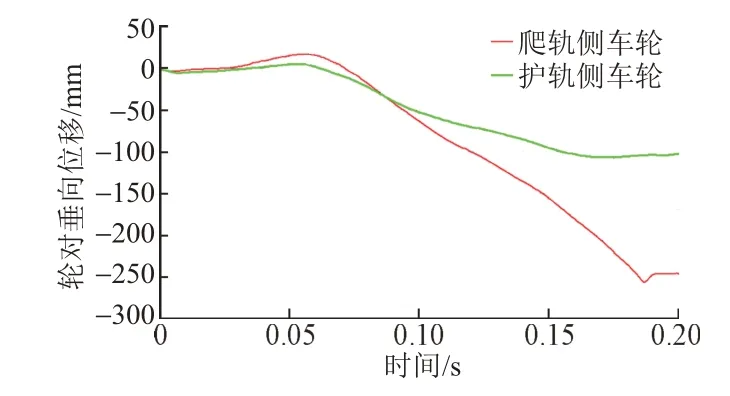
图9 轮对抬升量随时间变化曲线

3.5 护轨横向变形

护轨的横向变形决定了其对车轮的保护能力。接触点处护轨横向侧弯位移随时间变化曲线及最终形态见图10。可知：在0.105 s时车轮开始与护轨发生碰撞接触，护轨在车辆的横向挤压下发生了侧弯，继而发生横向变形；在0.2 s时护轨停止横向变形，横向侧弯位移保持在31 mm，能够满足铁路轨道设计规范要求。

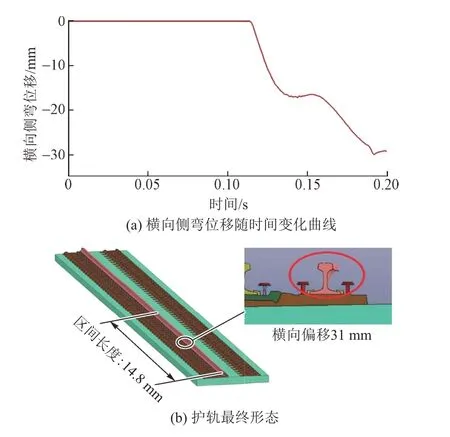
图10 接触点处护轨横向变形情况

3.6 道床受力状态

脱轨后轨道板的von Mises应力分布如图11所示。可知，车轮与钢轨碰撞的整个过程中，轨道板的最大von Mises应力为35.17 MPa，发生位置为轨道板护轨安装处靠近线路中心侧，能够满足C40混凝土的强度要求。

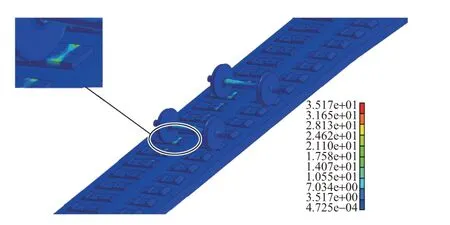
图11 轨道板von Mises应力分布（单位：MPa）

3.7 车辆偏移车辆限界情况

脱轨过程结束后，车辆以图12所示的稳定状态继续沿轨道向前滑行，未发生倾覆，说明护轨对车辆起到了重要的保护作用。该状态下，车体最外轮廓线横向偏移529 mm，车辆重心偏移轨道中心线396 mm。

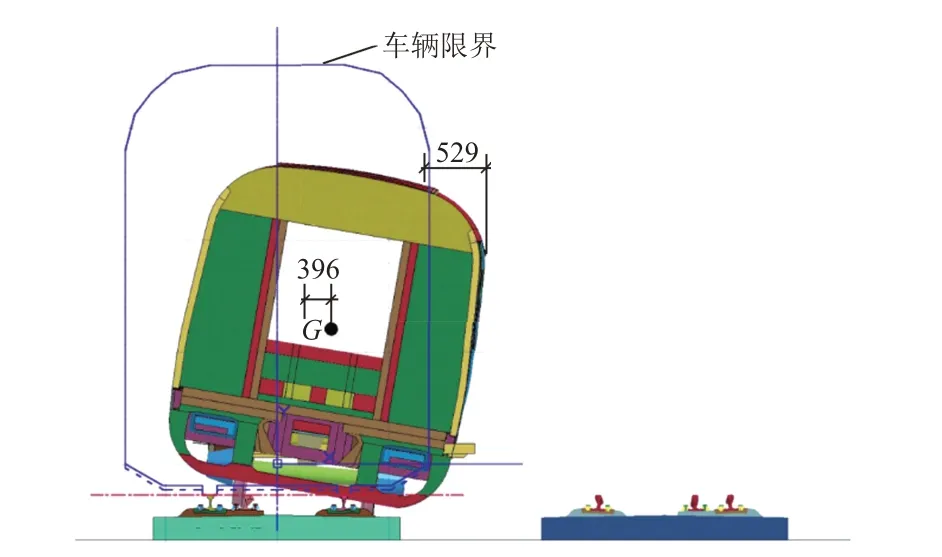
图12 车辆偏移形态（单位：mm）

4 结论

本文以非线性大变形有限元法为理论基础，以三维空间为设计与分析计算环境，利用BIM软件设计并建立了某轨道及其护轨结构的BIM模型，并基于BIM模型建立了该轨道与某车辆组成的脱轨系统有限元模型，通过LS⁃DYNA程序可视化研究了某高速铁路轨道护轨装置对车辆脱轨后的保护作用和自身的力学响应。主要结论如下：

1）车辆脱轨全过程中，轮轨之间的接触力上升及摩擦吸能集中在爬轨侧车轮与钢轨接触和护轨侧车轮与护轨接触两个阶段，考虑了柔性变形的有限元法使得列车在脱轨后撞击轨枕块和护轨的过程具有合理、可靠的传力过程和运动状态。

2）脱轨过程中，爬轨侧车轮爬至轨顶时车轮的垂向位移达到最大值，为17.622 mm，同时护轨侧车轮垂向位移也达到最大值，为5.540 mm，满足车辆运行安全性要求。

3）车轮与护轨碰撞接触过程中，护轨在车辆的横向挤压下发生侧弯，继而发生横向变形，其最大值为31 mm，满足铁路轨道设计规范要求。

4）脱轨后车轮与钢轨的碰撞过程中，轨道板的最大von Mises应力为35.17 MPa，发生在轨道板护轨安装处靠近线路中心侧，满足C40混凝土强度要求。

5）脱轨过程结束后，车体最外轮廓线横向偏移529 mm，车辆重心偏移轨道中心线396 mm，车辆以稳定的倾斜形态继续向前滑行，未发生倾覆，护轨对车辆起到了保护作用。